Коды с обнаружением ошибок реферат
Обновлено: 05.07.2024
1. Код с проверкой на четность.
Такой код образуется путем добавления к передаваемой комбинации, состоящей из k информационных символов, одного контрольного символа (0 или 1), так, чтобы общее число единиц в передаваемой комбинации было четным.
Пример 5.1 . Построим коды для проверки на четность, где k - исходные комбинации, r - контрольные символы.
Определим, каковы обнаруживающие свойства этого кода. Вероятность Poo обнаружения ошибок будет равна
Так как вероятность ошибок является весьма малой величиной, то можно ограничится
Вероятность появления всевозможных ошибок, как обнаруживаемых так и не обнаруживаемых, равна , где - вероятность отсутствия искажений в кодовой комбинации. Тогда .
При передаче большого количества кодовых комбинаций Nk , число кодовых комбинаций, в которых ошибки обнаруживаются, равно:
Общее количество комбинаций с обнаруживаемыми и не обнаруживаемыми ошибками равно
Тогда коэффициент обнаружения K обн для кода с четной защитой будет равен
Например, для кода с k =5 и вероятностью ошибки коэффициент обнаружения составит . То есть 90% ошибок обнаруживаем, при этом избыточность будет составлять или 17%.
2. Код с постоянным весом.
Этот код содержит постоянное число единиц и нулей. Число кодовых комбинаций составит
Пример 5.2. Коды с двумя единицами из пяти и тремя единицами из семи.
Этот код позволяет обнаруживать любые одиночные ошибки и часть многократных ошибок. Не обнаруживаются этим кодом только ошибки смещения, когда одновременно одна единица переходит в ноль и один ноль переходит в единицу, два ноля и две единицы меняются на обратные символы и т.д.
Рассмотрим код с тремя единицами из семи. Для этого кода возможны смещения трех типов.
Вероятность появления не обнаруживаемых ошибок смещения
Вероятность появления всевозможных ошибок как обнаруживаемых, так и не обнаруживаемых будет составлять
Вероятность обнаруживаемых ошибок . Тогда коэффициент обнаружения будет равен
Например, код при коэффициент обнаружения составит , избыточность L =27%.
3. Корреляционный код (Код с удвоением). Элементы данного кода заменяются двумя символами, единица ‘1’ преобразуется в 10, а ноль ‘0’ в 01.
Вместо комбинации 1010011 передается 10011001011010. Ошибка обнаруживается в том случае, если в парных элементах будут одинаковые символы 00 или 11 (вместо 01 и 10).
Например, при k =5, n =10 и вероятности ошибки , . Но при этом избыточность будет составлять 50%.
4. Инверсный код. К исходной комбинации добавляется такая же комбинация по длине. В линию посылается удвоенное число символов. Если в исходной комбинации четное число единиц, то добавляемая комбинация повторяет исходную комбинацию, если нечетное, то добавляемая комбинация является инверсной по отношению к исходной.
Прием инверсного кода осуществляется в два этапа. На первом этапе суммируются единицы в первой основной группе символов. Если число единиц четное, то контрольные символы принимаются без изменения, если нечетное, то контрольные символы инвертируются. На втором этапе контрольные символы суммируются с информационными символами по модулю два. Нулевая сумма говорит об отсутствии ошибок. При ненулевой сумме, принятая комбинация бракуется. Покажем суммирование для принятых комбинаций без ошибок (1,3) и с ошибками (2,4).
Обнаруживающие способности данного кода достаточно велики. Данный код обнаруживает практически любые ошибки, кроме редких ошибок смещения, которые одновременно происходят как среди информационных символов, так и среди соответствующих контрольных. Например, при k =5, n =10 и . Коэффициент обнаружения будет составлять .
5. Код Грея. Код Грея используется для преобразования угла поворота тела вращения в код. Принцип работы можно представить по рис.5.2. На пластине, которая вращается на валу, сделаны отверстия, через которые может проходить свет. Причём, диск разбит на сектора, в которых и сделаны эти отверстия. При вращении, свет проходит через них, что приводит к срабатыванию фотоприёмников. При снятии информации в виде двоичных кодов может произойти существенная ошибка. Например, возьмем две соседние цифры 7 и 8. Двоичные коды этих цифр отличаются во всех разрядах.
Если ошибка произойдет в старшем разряде, то это приведет к максимальной ошибке, на 360 0 . А код Грея, это такой код в котором все соседние комбинации отличаются только одним символом, поэтому при переходе от изображения одного числа к изображению соседнего происходит изменение только на единицу младшего разряда. Ошибка будет минимальной.
Задача кодирования заключается в формировании по информационным словам a(x) кодовых слов (x) циклического (n,k)-кода, который по своей структуре может быть несистематическим и систематическим.
Формирование кодовых слов несистематического кода заключается в умножении многочлена a(x), отображающего информационную последовательность длины k, на порождающий многочлен, т.е. (x)=a(x)(g(x). Формирование кодовых слов систематического кода заключается в преобразовании информационной последовательности a(x) в соответствии с выражением (x)=a(x)x r +r(x).
Проверочная последовательность r(x) определяется двумя способами:
при использовании "классического" способа кодирования ;
при использовании способа кодирования, рекомендованного МККТТ ,
где x(1) r-1 - единичный многочлен степени (r-1).
Указанные выше математические операции выполняют кодеры несистематического и систематического кодов.
Способы декодирования с обнаружением ошибок
Процедура декодирования циклического кода с обнаружением ошибок, по аналогии с процессом кодирования, использует два способа:
- при кодировании "классическим" способом декодирование основано на использовании свойства делимости без остатка кодового многочлена (x) циклического (n,k)-кода на порождающий многочлен g(x). Поэтому алгоритм декодирования включает в себя деление принятого кодового слова, описываемого многочленом на g(x), вычисление и анализ остатка r(x). Если r(x)=0, то принятое кодовое слово считается неискаженным. Если r(x)0, то принятое кодовое слово стирается и формируется сигнал "ошибка".
- при кодировании способом МККТТ декодирование основано на свойстве получения определенного контрольного остатка R0 (x) при делении принятого кодового многочлена (x) на порождающий многочлен. Поэтому, если полученный при делении остаток , то принятое кодовое слово считается неискаженным. Если остаток , то принятое кодовое слово стирается и формируется сигнал "ошибка". Значение контрольного остатка определяется из выражения .
Способы декодирования с исправлением ошибок и схемная реализация декодирующих устройств
Декодирование циклического кода в режиме исправления ошибок можно осуществлять различными способами. Ниже излагаются два способа, являющиеся наиболее простыми.
В основу первого способа положено использование таблицы синдромов (декодирования), в которой каждому многочлену или образцу ошибок ei (x), соответствует определенный синдром Si (x), представляющий остаток от деления принятого кодового слова и соответствующего ему ei (x) на g(x). Процедура декодирования следующая. Принятое кодовое слово делится на g(x), определяется Si (x) и соответствующий ему многочлен ei (x), а затем суммируется с ei (x). В результате получаем исправленное кодовое слово, т.е. .
В состав декодера входят: вычислитель синдрома (ВС), два регистра сдвига RG1 и RG2, постоянное запоминающее устройство (ПЗУ), которое содержит слова длины n, соответствующие многочленам ошибок ei (x).
Принятое кодовое слово поступает на вход вычислителя синдрома, где осуществляется деление его на g(x) и формирование Si (x), и одновременно - на вход RG2, где накапливается. Синдром Si (x) используется в качестве адреса, по которому из ПЗУ в регистр RG1 записывается ei (x), соответствующий синдрому Si (x). Перечисленные операции завершаются за n тактов. В течение последующих n тактов происходит поэлементное суммирование содержимого RG2 и RG1, т.е. операция , и исправление. ошибок.
В основе второго способа исправления ошибок, позволяющего значительно сократить объем используемых табличных синдромов и существенно упростить схему декодера, лежат следующие положения:
1. Синдром Si (x), соответствующий принятому кодовому слову равен остатку от деления на g(x), а также остатку от деления соответствующего многочлена ошибок ei(x) на g(x), т.е. .
2. Если Si (x) соответствует и ei (x), то x( Si (x) является синдромом, который соответствует и или .
3. При исправлении ошибок используются синдромы образцов ошибок только с ненулевым коэффициентом в старшем разряде.
Поэтому при реализации этого способа множество всех образцов ошибок разбивается на классы эквивалентности. Каждый класс представляет циклический сдвиг одного образца ошибок, а синдром этого класса соответствует образцу ошибок с ненулевым старшим разрядом. Если вычисленный синдром принадлежит одному из классов эквивалентности образцов исправляемых ошибок, то старший символ кодового слова исправляется. Затем принятое слово и синдром циклически сдвигается, а процесс нахождения в предыдущей по старшинству позиции повторяется.
Для исправления ошибок, принадлежащих данному классу эквивалентности, нужно произвести n циклических сдвигов.

Простейшим является декодер Меггитта. В состав декодера входят: вычислитель синдрома, осуществляющий деление кодового слова на g(x) и формирование соответствующего синдрома; блок декодеров (ДК), который настроен на синдромы всех образцов исправляемых ошибок с ненулевыми старшими разрядами; регистр сдвига RG.
При поступлении на вход схемы кодового слова его символы заполняют регистр RG, а в вычислителе формируется соответствующий синдром Si (x). Вычисленный синдром сравнивается со всеми табличными синдромами, заложенными в схему блока ДК, и в случае совпадения с одним из них на его выходе формируется сигнал, который исправляет ошибочный символ, находящийся в старшем разряде регистра. После этого содержимое вычислителя и RG циклически сдвигается на один шаг. Этот сдвиг реализует операции и . Если новый синдром совпадает с одним из табличных синдромов, то это означает, что произошла ошибка во втором по старшинству символе кодового слова, который, перейдя в старший разряд RG, исправляется. Затем производится новый циклический сдвиг на одну позицию и новая проверка на совпадение синдромов. После повторения этого процесса n раз в RG будет сформировано исправленное кодовое слово. Введение обратной связи для RG не обязательно, так как в процессе исправления ошибок символы кодового слова поступают на выход декодера.
Пример. Рассмотрим схему и работу декодера Меггитта циклического (15,7)-кода, обеспечивающего исправление одиночных и двойных ошибок, с g(x)=x 8 + x 7 + x 6 + x 4 +1 (см. рисунок 1).






Блок декодеров настраивается на 15 синдромов, которые представлены в таблице 1 и соответствуют классам эквивалентности с образцами ошибок в старшем разряде.
| Таблица 1 | |||||
| № | |||||
| е(х) | S(x) | № | е(х) | S(x) | |
| 1 | x 14 | x 7 + x 6 +x 5 + x 3 | 9 | x 14 + x 6 | |
| 2 | x 14 + x 13 | x 7 + x 4 +x 3 + x 2 | 10 | x 14 + x 5 | x 7 + x 6 +x 3 |
| 3 | x 14 + x 12 | x 7 + x 6 +x 4 + x | 11 | x 14 + x 4 | x 7 + x 6 +x 5 + x 4 +x 3 |
| 4 | x 14 + x 11 | 12 | x 14 + x 3 | x 7 + x 6 +x 5 | |
| 5 | x 14 + x 10 | 13 | x 14 + x 2 | x 7 + x 6 +x 5 + x 3 +x 2 | |
| 6 | x 14 + x 9 | 14 | x 14 + x 1 | x 7 + x 6 +x 5 + x 3 +x | |
| 7 | x 14 + x 8 | 15 | x 14 + x 0 | x 7 + x 6 +x 5 + x 3 +0 | |
| 8 | x 14 + x 7 |
Допустим, что ошибки в 3 и 5 разрядах, т.е. им соответствует многочлен ошибки e(x)=x 12 +x 10 .

При поступлении на вход декодера искаженного кодового слова он заполняет регистр и в вычислителе формируется синдром .
Блок декодеров не реагирует на этот синдром.

Затем происходит сдвиг кодового слова в RG, а в BC формируется новый синдром .
Блок декодеров и в этом случае не срабатывает.

При следующем сдвиге кодового слова в RG первый искаженный разряд занимает старшую позицию в RG, а в BC формируется синдром , от которого срабатывает БДК. В результате исправляется первая ошибка.

Следующим сдвиг приводит к формированию синдрома .
Этот синдром соответствует многочлену ошибки e(x)=x 13 +x 0 , т.к. первый искаженный разряд по обратной связи должен занять младшую позицию RG.
На синдром S(13,0) блок декодеров не реагирует.

При следующем сдвиге кодового слова в RG второй искаженный разряд занимает старшую позицию в RG, а в BC формируется синдром , от которого срабатывает БДК. В результате исправляется вторая ошибка в кодовом слове.
Коды Рида-Соломона (РС)
Коды РС являются недвоичными циклическими кодами, символы кодовых слов которых берутся из конечного поля GF(q). Здесь q степень некоторого простого числа, например q=2 m .
Допустим, что РС-код построен над GF(8), которое является расширением поля GF(2) по модулю примитивного многочлена f(z)=z 3 +z+1. В этом случае символы кодовых слов кода будут иметь значения, представленные в таблице 2.
| Таблица 2 | |||||
| 000 | 0 | 0 | 011 | z+1 | 3 |
| 001 | 1 | 0 | 110 | z 2 +z | 4 |
| 010 | z | 1 | 111 | z 2 +z+1 | 5 |
| 100 | z 2 | 2 | 101 | z 2 +1 | 6 |

Кодовые слова РС-кода отображаются в виде многочленов
,
где N - длина кода; Vi - q-ичные коэффициенты (символы кодовых слов), которые могут принимать любое значение из GF(q).

Эти коэффициенты как это следует из таблицы, также отображаются многочленами с двоичными коэффициентами . Коды РС являются максимальными, т.к. при длине кода N и информационной последовательности k они обладают наибольшим кодовым расстоянием d=N-k+1.
Порождающим многочленом g(x) РС-кода является делитель двучлена x N +1 степени меньшей N с коэффициентами из GF(q) при условии, что элементы этого поля являются корнями g(x). Здесь - примитивный элемент GF(q).

На основе этого определения, а также теоремы Безу, выражение для порождающего многочлена РС-кода будет иметь вид .
Степень g(x) равна d-1=N-k=R.

В РС-кодах принадлежность кодовых слов данному коду определяется выполнением d-1 уравнений в соответствии с выражением (*), где Vi - символы-коэффициенты из GF(q); z0 , z1 . zN-1 - ненулевые элементы GF(q).
Элементы z0 , z1 . zN-1 называются локаторами, т.е. указывающими на номер позиции символа кодового слова.
Например, указателем i - позиции является локатор zi или элемент i GF(q).
Так как все локаторы должны быть различны и причем ненулевыми, то их число в GF(q) равно q-1. Следовательно, такое количество символов должно быть в кодовых словах кода.Поэтому обычно длина РС-кода определяется из выражения N=q-1.

Пример. Допустим, что длина РС-кода равна N, кодовое расстояние d=3, то в соответствии с (*) проверочными уравнениями будут
1. Циклический сдвиг кодовых слов, символы которых принимают значение из GF(q), порождает новые кодовые слова этого же кода.
2. Сумма по mod2 двух и более кодовых слов дает кодовое слово, принадлежащее этому же коду.
3. Кодовое расстояние РС-кода определяется не по двоичным элементам, а по q-ичным символам.

4. В РС-коде, исправляющем tu ошибок порождающий многочлен определяется из выражения . Обычно m0 принимают равным 1. Однако, с помощью разумного выбора значения m0 , иногда можно упростить схему кодера.

5. Корректирующие способности РС-кода определяются его кодовым расстоянием.
где T0 и Tu - длина пакетов, в которых обнаруживаются и исправляются ошибки.
Обнаружение ошибок в кодовых словах состоит в проверке условий ((), т.е. определении синдрома , элементы которого определяются из выражения .
Пример. Требуется сформировать кодовое слово РС-кода над GF(2 3 ), соответствующее двоичной информационной последовательности a(1,0)=000000011100101.
Так как m=3, то каждый q-ичный символ кода состоит из трех двоичных элементов. Поэтому с учетом таблицы 6 a(x)= 3 x 2 + 2 x+ 6 .

Определяем параметры кода. N=q-1=7; k=5; R=2; d=N-k+1=3;
.
Кодовое слово формируется в соответствии с выражением. ,
где .

В результате или в двоичной форме V(1,0)=000.000.011.100.101.101.101.
2. Метрология и радиоизмерения в телекоммуникационных системах. Учебник для ВУЗов. / В.И.Нефедов, В.И.Халкин, Е.В.Федоров и др. – М.: Высшая школа, 2001 г. – 383с.
3. Цапенко М.П. Измерительные информационные системы. - . – М.: Энергоатом издат, 2005. - 440с.
4. Зюко А.Г. , Кловский Д.Д., Назаров М.В., Финк Л.М. Теория передачи сигналов. М: Радио и связь, 2001 г. –368 с.
История кодирования, контролирующего ошибки, началась в 1948 г. публикацией знаменитой статьи Клода Шеннона. Шеннон показал, что с каждым каналом связано измеряемое в битах в секунду и называемое пропускной способностью канала число С, имеющее следующее значение. Если требуемая от системы связи скорость передачи информации R (измеряемая в битах в секунду) меньше С, то, используя коды, контролирующие ошибки, для данного канала можно построить такую систему связи, что вероятность ошибки на выходе будет сколь угодно мала.
В самом деле, из шенноновской теории информации следует тот важный вывод, что построение слишком хороших каналов является расточительством; экономически выгоднее использовать кодирование.
Содержание работы
Введение. 3
1. Обнаружение ошибок. 4
2. Коррекция ошибок. 6
3. Циклические коды. 11
4. Линейные блочные коды. 15
Заключение 18
Литература. 19
Файлы: 1 файл
РЕФЕРАТ Обнаружение и коррекция ошибок при передаче информации..docx
1. Обнаружение ошибок. 4
2. Коррекция ошибок. 6
3. Циклические коды. 11
4. Линейные блочные коды. 15
Введение.
История кодирования, контролирующего ошибки, началась в 1948 г. публикацией знаменитой статьи Клода Шеннона. Шеннон показал, что с каждым каналом связано измеряемое в битах в секунду и называемое пропускной способностью канала число С, имеющее следующее значение. Если требуемая от системы связи скорость передачи информации R (измеряемая в битах в секунду) меньше С, то, используя коды, контролирующие ошибки, для данного канала можно построить такую систему связи, что вероятность ошибки на выходе будет сколь угодно мала.
В самом деле, из шенноновской теории информации следует тот важный вывод, что построение слишком хороших каналов является расточительством; экономически выгоднее использовать кодирование. В следующем десятилетии решению этой увлекательной задачи уделялось меньше внимания; вместо этого исследователи кодов предприняли длительную атаку по двум основным направлениям.
Первое направление носило чисто алгебраический характер и преимущественно рассматривало блоковые коды. Первые блоковые коды были введены в 1950 г., когда Хэмминг описал класс блоковых кодов, исправляющих одиночные ошибки.
Второе направление исследований по кодированию носило скорее вероятностный характер. Ранние исследования были связаны с оценками вероятностей ошибки для лучших семейств блоковых кодов, несмотря на то, что эти лучшие коды не были известны.
Так как развитие кодов, контролирующих ошибки, первоначально стимулировалось задачами связи, терминология теории кодирования проистекает из теории связи. Построенные коды, однако, имеют много других приложений. Коды используются для защиты данных в памяти вычислительных устройств и на цифровых лентах и дисках, а также для защиты от неправильного функционирования или шумов в цифровых логических цепях.
1. Обнаружение ошибок.
Каналы передачи данных ненадежны, да и само оборудование обработки информации работает со сбоями. По этой причине важную роль приобретают механизмы детектирования ошибок. Ведь если ошибка обнаружена, можно осуществить повторную передачу данных и решить проблему. Если исходный код по своей длине равен полученному коду, обнаружить ошибку передачи не предоставляется возможным.
Простейшим способом обнаружения ошибок является контроль по четности. Обычно контролируется передача блока данных (М бит). Этому блоку ставится в соответствие кодовое слово длиной N бит, причем N>M. Избыточность кода характеризуется величиной 1–M/N. Вероятность обнаружения ошибки определяется отношением M/N (чем меньше это отношение, тем выше вероятность обнаружения ошибки, но и выше избыточность).
При передаче информации она кодируется таким образом, чтобы с одной стороны характеризовать ее минимальным числом символов, а с другой – минимизировать вероятность ошибки при декодировании получателем. Для выбора типа кодирования важную роль играет так называемое расстояние Хэмминга.
Пусть А и Б две двоичные кодовые последовательности равной длины. Расстояние Хэмминга между двумя этими кодовыми последовательностями равно числу символов, которыми они отличаются. Например, расстояние Хэмминга между кодами 00111 и 10101 равно 2.
Можно показать, что для детектирования ошибок в n битах, схема кодирования требует применения кодовых слов с расстоянием Хэмминга не менее N+1. Можно также показать, что для исправления ошибок в N битах необходима схема кодирования с расстоянием Хэмминга между кодами не менее 2N+1. Таким образом, конструируя код, мы пытаемся обеспечить расстояние Хэмминга между возможными кодовыми последовательностями больше, чем оно может возникнуть из-за ошибок.
Широко распространены коды с одиночным битом четности. В этих кодах к каждым М бит добавляется 1 бит, значение которого определяется четностью (или нечетностью) суммы этих М бит. Так, например, для двухбитовых кодов 00, 01, 10, 11 кодами с контролем четности будут 000, 011, 101 и 110. Если в процессе передачи один бит будет передан неверно, четность кода из М+1 бита изменится.
Предположим, что частота ошибок (BER) равна р=10 -4 . В этом случае вероятность передачи 8 бит с ошибкой составит: 1–(1–p) 8 =7,9∙10 -4 .
Добавление бита четности позволяет детектировать любую ошибку в одном из переданных битах. Здесь вероятность ошибки в одном из 9 бит равна 9p(1–p) 8 . Вероятность же реализации необнаруженной ошибки составит: 1– (1– p) 9 – 9p(1– p) 8 = 3,6∙10 -7 .
Таким образом, добавление бита четности уменьшает вероятность необнаруженной ошибки почти в 1000 раз. Использование одного бита четности типично для асинхронного метода передачи. В синхронных каналах чаще используется вычисление и передача битов четности как для строк, так и для столбцов передаваемого массива данных. Такая схема позволяет не только регистрировать но и исправлять ошибки в одном из битов переданного блока.
Контроль по четности достаточно эффективен для выявления одиночных и множественных ошибок в условиях, когда они являются независимыми. При возникновении ошибок в кластерах бит метод контроля четности неэффективен и тогда предпочтительнее метод вычисления циклических сумм (CRC).
2. Коррекция ошибок.
Но существуют и более простые методы коррекции ошибок. Например, передача блока данных, содержащего N строк и M столбцов, снабженных битами четности для каждой строки и столбца. Обнаружение ошибки четности в строке i и столбце j указывает на бит, который должен быть инвертирован. Может показаться, что в случае, когда неверны два бита, находящиеся в разных строках и столбцах, они также могут быть исправлены. Но это не так. Ведь нельзя разделить варианты i1,j1 - i2,j2 и i1,j2 - i2,j1. Этот метод может быть развит путем формирования блока данных с N строками, M столбцами и K слоями. Здесь биты четности формируются для всех строк и столбцов каждого из слоев, а также битов, имеющих одинаковые номера строк и столбцов i,j. Полное число битов четности в этом случае равно (N+M+1)×K +(N+1)×(M+1). Если M=N=K=8, число бит данных составит 512, а число бит четности - 217. Нетрудно видеть, что в этом случае число исправляемых ошибок будет больше 1. (Рис. 1).
Рис. 1. Метод коррекции более одной ошибки в блоке данных
(битам данных соответствуют окрашенные квадраты)
Коды Хэмминга наиболее известные и, вероятно, первые из самоконтролирующихся и самокорректирующихся кодов. Построены они применительно к двоичной системе счисления.
Для того, чтобы понять работу данного алгоритма, рассмотрим пример.
Прежде всего, необходимо вставить контрольные биты. Они вставляются в строго определённых местах — это позиции с номерами, равными степеням двойки. В нашем случае (при длине информационного слова в 16 бит) это будут позиции 1, 2, 4, 8, 16. Соответственно, у нас получилось 5 контрольных бит (выделенные):
Вычисление контрольных бит.
Теперь необходимо вычислить значение каждого контрольного бита. Значение каждого контрольного бита зависит от значений информационных бит, но не от всех, а только от тех, которые этот контрольных бит контролирует. Для того, чтобы понять, за какие биты отвечает каждых контрольный бит необходимо понять очень простую закономерность: контрольный бит с номером N контролирует все последующие N бит через каждые N бит, начиная с позиции N.
Но как же вычислить значение каждого контрольного бита? Делается это очень просто: берём каждый контрольный бит и смотрим, сколько среди контролируемых им битов единиц, получаем некоторое целое число и, если оно чётное, то ставим ноль, в противном случае ставим единицу.
Высчитав контрольные биты для нашего информационного слова получаем следующее:
и для второй части:
Декодирование и исправление ошибок.
Вся вторая часть алгоритма заключается в том, что необходимо заново вычислить все контрольные биты (так же как и в первой части) и сравнить их с контрольными битами, которые мы получили. Так, посчитав контрольные биты с неправильным 11-ым битом мы получим такую картину:
Метод коррекции ошибок FEC.
Для FEC(Forward Error Correction)-кодирования иногда используется метод сверки, который впервые был применен в 1955 году. Главной особенностью этого метода является сильная зависимость кодирования от предыдущих информационных битов и высокие требования к объему памяти. FEC-код обычно просматривает при декодировании 2-8 бит десятки или даже сотни бит.
В 1967 году Эндрю Витерби (Andrew Viterbi) разработал технику декодирования, которая стала стандартной для кодов свертки. Эта методика требовала меньше памяти. Метод свертки более эффективен, когда ошибки распределены случайным образом, а не группируются в кластеры. Работа же с кластерами ошибок более эффективна при использовании алгебраического кодирования.
Одним из широко используемых разновидностей коррекции ошибок является турбо кодирование, разработанное американской аэрокосмической корпорацией. В этой схеме комбинируется два или более относительно простых кодов свертки. В FEC, также как и в других методах коррекции ошибок (коды Хэмминга, алгоритм Рида-Соломона и др.), блоки данных из k бит снабжаются кодами четности, которые пересылаются вместе с данными, и обеспечивают не только детектирование, но и исправление ошибок. Каждый дополнительный (избыточный) бит является сложной функцией многих исходных информационных бит. Исходная информация может содержаться в выходном передаваемом коде, тогда такой код называется систематическим, а может и не содержаться.
Аннотация: Контроль по четности, CRC, алгоритм Хэмминга. Введение в коды Рида-Соломона: принципы, архитектура и реализация. Метод коррекции ошибок FEC (Forward Error Correction).
Каналы передачи данных ненадежны ( шумы , наводки и т.д.), да и само оборудование обработки информации работает со сбоями. По этой причине важную роль приобретают механизмы детектирования ошибок. Ведь если ошибка обнаружена, можно осуществить повторную передачу данных и решить проблему. Если исходный код по своей длине равен полученному коду, обнаружить ошибку передачи не предоставляется возможным. Можно, конечно, передать код дважды и сравнить, но это уже двойная избыточность .
Простейшим способом обнаружения ошибок является контроль по четности . Обычно контролируется передача блока данных ( М бит ). Этому блоку ставится в соответствие кодовое слово длиной N бит , причем N>M . Избыточность кода характеризуется величиной 1-M/N . Вероятность обнаружения ошибки определяется отношением M/N (чем меньше это отношение , тем выше вероятность обнаружения ошибки, но и выше избыточность ).
При передаче информации она кодируется таким образом, чтобы с одной стороны характеризовать ее минимальным числом символов, а с другой – минимизировать вероятность ошибки при декодировании получателем. Для выбора типа кодирования важную роль играет так называемое расстояние Хэмминга .
Пусть А и Б — две двоичные кодовые последовательности равной длины. Расстояние Хэмминга между двумя этими кодовыми последовательностями равно числу символов, которыми они отличаются. Например, расстояние Хэмминга между кодами 00111 и 10101 равно 2.
Можно показать, что для детектирования ошибок в n битах схема кодирования требует применения кодовых слов с расстоянием Хэмминга не менее N + 1 . Можно также показать, что для исправления ошибок в N битах необходима схема кодирования с расстоянием Хэмминга между кодами не менее 2N + 1 . Таким образом, конструируя код, мы пытаемся обеспечить расстояние Хэмминга между возможными кодовыми последовательностями большее, чем оно может возникнуть из-за ошибок.
Широко распространены коды с одиночным битом четности . В этих кодах к каждым М бит добавляется 1 бит , значение которого определяется четностью (или нечетностью) суммы этих М бит . Так, например, для двухбитовых кодов 00 , 01 , 10 , 11 кодами с контролем четности будут 000 , 011 , 101 и 110 . Если в процессе передачи один бит будет передан неверно, четность кода из М+1 бита изменится.
Предположим, что частота ошибок ( BER – Bit Error Rate ) равна р = 10 -4 . В этом случае вероятность передачи 8 бит с ошибкой составит 1 – (1 – p) 8 = 7,9 х 10 -4 . Добавление бита четности позволяет детектировать любую ошибку в одном из переданных битах. Здесь вероятность ошибки в одном из 9 битов равна 9p(1 – p) 8 . Вероятность же реализации необнаруженной ошибки составит 1 – (1 – p) 9 – 9p(1 – p) 8 = 3,6 x 10 -7 . Таким образом, добавление бита четности уменьшает вероятность необнаруженной ошибки почти в 1000 раз. Использование одного бита четности типично для асинхронного метода передачи. В синхронных каналах чаще используется вычисление и передача битов четности как для строк, так и для столбцов передаваемого массива данных. Такая схема позволяет не только регистрировать, но и исправлять ошибки в одном из битов переданного блока.
Контроль по четности достаточно эффективен для выявления одиночных и множественных ошибок в условиях, когда они являются независимыми. При возникновении ошибок в кластерах бит метод контроля четности неэффективен, и тогда предпочтительнее метод вычисления циклических сумм ( CRC — Cyclic Redundancy Check ). В этом методе передаваемый кадр делится на специально подобранный образующий полином . Дополнение остатка от деления и является контрольной суммой.
В Ethernet вычисление CRC производится аппаратно. На рис. 4.1 показан пример реализации аппаратного расчета CRC для образующего полинома R(x) = 1 + x 2 + x 3 + x 5 + x 7 . В этой схеме входной код приходит слева.
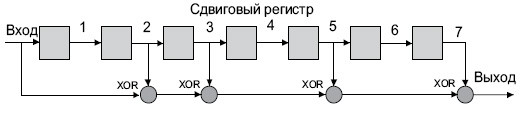
Эффективность CRC для обнаружения ошибок на многие порядки выше простого контроля четности . В настоящее время стандартизовано несколько типов образующих полиномов . Для оценочных целей можно считать, что вероятность невыявления ошибки в случае использования CRC , если ошибка на самом деле имеет место , равна (1/2) r , где r — степень образующего полинома .
4.1. Алгоритмы коррекции ошибок
Читайте также:

