Геометрические доказательства формул сокращенного умножения реферат
Обновлено: 07.07.2024
Формулы сокращенного умножения (ФСУ) применяются для возведения в степень и умножения чисел и выражений. Часто эти формулы позволяют произвести вычисления более компактно и быстро.
В данной статье мы перечислим основные формулы сокращенного умножения, сгруппируем их в таблицу, рассмотрим примеры использования этих формул, а также остановимся на принципах доказательств формул сокращенного умножения.
Формулы сокращенного умножения. Таблица
Впервые тема ФСУ рассматривается в рамках курса "Алгебра" за 7 класс. Приведем ниже 7 основных формул.
Формулы сокращенного умножения
- формула квадрата суммы: a + b 2 = a 2 + 2 a b + b 2
- формула квадрата разности: a - b 2 = a 2 - 2 a b + b 2
- формула куба суммы: a + b 3 = a 3 + 3 a 2 b + 3 a b 2 + b 3
- формула куба разности: a - b 3 = a 3 - 3 a 2 b + 3 a b 2 - b 3
- формула разности квадратов: a 2 - b 2 = a - b a + b
- формула суммы кубов: a 3 + b 3 = a + b a 2 - a b + b 2
- формула разности кубов: a 3 - b 3 = a - b a 2 + a b + b 2
Буквами a, b, c в данных выражениях могут быть любые числа, переменные или выражения. Для удобства использования лучше выучить семь основных формул наизусть. Сведем их в таблицу и приведем ниже, обведя рамкой.

Первые четыре формулы позволяют вычислять соответственно квадрат или куб суммы или разности двух выражений.
Пятая формула вычисляет разность квадратов выражений путем произведения их суммы и разности.
Шестая и седьмая формулы - соответственно умножение суммы и разности выражений на неполный квадрат разности и неполный квадрат суммы.
Формула сокращенного умножения иногда еще называют тождествами сокращенного умножения. В этом нет ничего удивительного, так как каждое равенство представляет собой тождество.
При решении практических примеров часто используют формулы сокращенного умножения с переставленными местами левыми и правыми частями. Это особенно удобно, когда имеет место разложение многочлена на множители.

Дополнительные формулы сокращенного умножения
Не будем ограничиваться курсом 7 класса по алгебре и добавим в нашу таблицу ФСУ еще несколько формул.
Во-первых, рассмотрим формулу бинома Ньютона.
a + b n = C n 0 · a n + C n 1 · a n - 1 · b + C n 2 · a n - 2 · b 2 + . . + C n n - 1 · a · b n - 1 + C n n · b n
Здесь C n k - биномиальные коэффициенты, которые стоят в строке под номером n в треугольнике паскаля. Биномиальные коэффициенты вычисляются по формуле:
C n k = n ! k ! · ( n - k ) ! = n ( n - 1 ) ( n - 2 ) . . ( n - ( k - 1 ) ) k !
Как видим, ФСУ для квадрата и куба разности и суммы - это частный случай формулы бинома Ньютона при n=2 и n=3соответственно.
Но что, если слагаемых в сумме, которую нужно возвести в степень, больше, чем два? Полезной будет формула квадрата суммы трех, четырех и более слагаемых.
a 1 + a 2 + . . + a n 2 = a 1 2 + a 2 2 + . . + a n 2 + 2 a 1 a 2 + 2 a 1 a 3 + . . + 2 a 1 a n + 2 a 2 a 3 + 2 a 2 a 4 + . . + 2 a 2 a n + 2 a n - 1 a n
Как читать эту формулу? Квадрат суммы n слагаемых равен сумме квадратов всех слагаемых и удвоенных произведений всех возможных пар этих слагаемых.
Еще одна формула, которая может пригодится - формула формула разности n-ых степеней двух слагаемых.
a n - b n = a - b a n - 1 + a n - 2 b + a n - 3 b 2 + . . + a 2 b n - 2 + b n - 1
Эту формулу обычно разделяют на две формулы - соответственно для четных и нечетных степеней.
Для четных показателей 2m:
a 2 m - b 2 m = a 2 - b 2 a 2 m - 2 + a 2 m - 4 b 2 + a 2 m - 6 b 4 + . . + b 2 m - 2
Для нечетных показателей 2m+1:
a 2 m + 1 - b 2 m + 1 = a 2 - b 2 a 2 m + a 2 m - 1 b + a 2 m - 2 b 2 + . . + b 2 m
Формулы разности квадратов и разности кубов, как вы догадались, являются частными случаями этой формулы при n = 2 и n = 3 соответственно. Для разности кубов b также заменяется на - b .
Как читать формулы сокращенного умножения?
Дадим соответствующие формулировки для каждой формулы, но сначала разберемся с принципом чтения формул. Удобнее всего делать это на примере. Возьмем самую первую формулу квадрата суммы двух чисел.
a + b 2 = a 2 + 2 a b + b 2 .
Говорят: квадрат суммы двух выражений a и b равен сумме квадрата первого выражения, удвоенного произведения выражений и квадрата второго выражения.
Все остальные формулы читаются аналогично. Для квадрата разности a - b 2 = a 2 - 2 a b + b 2 запишем:
квадрат разности двух выражений a и b равен сумме квадратов этих выражений минус удвоенное произведение первого и второго выражения.
Прочитаем формулу a + b 3 = a 3 + 3 a 2 b + 3 a b 2 + b 3 . Куб суммы двух выражений a и b равен сумме кубов этих выражений, утроенного произведения квадрата первого выражения на второе и утроенного произведения квадрата второго выражения на первое выражение.
Переходим к чтению формулы для разности кубов a - b 3 = a 3 - 3 a 2 b + 3 a b 2 - b 3 . Куб разности двух выражений a и b равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе, плюс утроенное произведение квадрата второго выражения на первое выражение, минус куб второго выражения.
Пятая формула a 2 - b 2 = a - b a + b (разность квадратов) читается так: разность квадратов двух выражений равна произведению разности и суммы двух выражений.
Выражения типа a 2 + a b + b 2 и a 2 - a b + b 2 для удобства называют соответственно неполным квадратом суммы и неполным квадратом разности.
С учетом этого, формулы суммы и разности кубов прочитаются так:
Сумма кубов двух выражений равна произведению суммы этих выражений на неполный квадрат их разности.
Разность кубов двух выражений равна произведению разности этих выражений на неполный квадрат их суммы.
Доказательство ФСУ
Доказать ФСУ довольно просто. Основываясь на свойствах умножения, проведем умножение частей формул в скобках.
Для примера рассмотрим формулу квадрата разности.
a - b 2 = a 2 - 2 a b + b 2 .
Чтобы возвести выражение во вторую степень нужно это выражение умножить само на себя.
a - b 2 = a - b a - b .
a - b a - b = a 2 - a b - b a + b 2 = a 2 - 2 a b + b 2 .
Формула доказана. Остальные ФСУ доказываются аналогично.
Примеры применения ФСУ
Цель использования формул сокращенного умножения - быстрое и краткое умножение и возведение выражений в степень. Однако, это не вся сфера применения ФСУ. Они широко используются при сокращении выражений, сокращении дробей, разложении многочленов на множители. Приведем примеры.
Упростим выражение 9 y - ( 1 + 3 y ) 2 .
Применим формулу суммы квадратов и получим:
9 y - ( 1 + 3 y ) 2 = 9 y - ( 1 + 6 y + 9 y 2 ) = 9 y - 1 - 6 y - 9 y 2 = 3 y - 1 - 9 y 2
Сократим дробь 8 x 3 - z 6 4 x 2 - z 4 .
Замечаем, что выражение в числителе - разность кубов, а в знаменателе - разность квадратов.
8 x 3 - z 6 4 x 2 - z 4 = 2 x - z ( 4 x 2 + 2 x z + z 4 ) 2 x - z 2 x + z .
Сокращаем и получаем:
8 x 3 - z 6 4 x 2 - z 4 = ( 4 x 2 + 2 x z + z 4 ) 2 x + z
Также ФСУ помогают вычислять значения выражений. Главное - уметь заметить, где применить формулу. Покажем это на примере.
Возведем в квадрат число 79 . Вместо громоздких вычислений, запишем:
79 = 80 - 1 ; 79 2 = 80 - 1 2 = 6400 - 160 + 1 = 6241 .
Казалось бы, сложное вычисление проведено быстро всего лишь с использованием формул сокращенного умножения и таблицы умножения.
Еще один важный момент - выделение квадрата двучлена. Выражение 4 x 2 + 4 x - 3 можно преобразовать в вид 2 x 2 + 2 · 2 · x · 1 + 1 2 - 4 = 2 x + 1 2 - 4 . Такие преобразования широко используются в интегрировании.
Целью реферата является изучение формул сокращённого умножения
(далее ФСУ) и их применения в решении задач и примеров.
Задачи:
проанализировать ФСУ, изучаемые по школьной программе;
познакомиться с ФСУ, не изучаемыми по школьной программе;
попытаться вывести своё ФСУ;
проанализировать применение ФСУ.
Содержание
1. Введение 3
2. Историческая справка 4
3. Формулы сокращенного умножения, изучаемые в школе 5
4. Формулы сокращенного умножения, не изучаемые по школьной программе 7
4.1. Треугольник Паскаля 7
4.2. Интересные свойства формул. 9
4.3. Другие полезные ФСУ. 9
5. Применение формул сокращённого умножения 10
5.1. Арифметические расчёты 10
5.2. Упрощение алгебраических выражений 10
5.3. Разложение многочлена на множители 10
6. Мои исследования 11
6.1. Квадрат трёхчлена -a-b-c 11
6.2. Куб трёхчлена -a-b-c 11
7. Заключение 12
8 Список используемой литературы 13
Работа содержит 1 файл
Формулы сокращенного умножения.doc
Формулы сокращённого умножения
Введение
Целью реферата является изучение формул сокращённого умножения
(далее ФСУ) и их применения в решении задач и примеров.
- проанализировать ФСУ, изучаемые по школьной программе;
- познакомиться с ФСУ, не изучаемыми по школьной программе;
- попытаться вывести своё ФСУ;
- проанализировать применение ФСУ.
- Квадрат суммы двух выражений равен квадрату первого плюс удвоенное произведение первого на второе плюс квадрат второго выражения:.
- Квадрат разности двух выражений равен квадрату первого минус удвоенное произведение первого на второе плюс квадрат второго выражения:
- Разность квадратов двух выражений равна произведению суммы этих выражений на их разность:
- Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого на второе плюс утроенное произведение первого на квадрат второго плюс куб второго выражения:
- Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого на второе плюс утроенное произведение первого на квадрат второго минус куб второго выражения:
- Сумма кубов двух выражений равна произведению суммы этих выражений на неполный квадрат их разности:
- Разность кубов двух выражений равна произведению разности этих выражений на неполный квадрат их суммы:
- Собрать сведения из истории математики о формулах сокращенного умножения.
- Доказать формулы сокращенного умножения, используя геометрические приемы
- Рассмотреть различные способы возведения в квадрат алгебраической суммы нескольких слагаемых.
- Выполнить модель, позволяющую находить квадрат и куб суммы двух чисел.
Немного теории: вспомним определения некоторых терминов, которые будут встречаться в реферате.
1. Одночлен - это произведение числовых и буквенных множителей.
2. Многочлен - это алгебраическая сумма нескольких одночленов.
3. Разложение многочлена на множители - преобразование многочлена в произведение 2-х или нескольких более простых многочленов.
4. Многочлен вида (а 2 +ав+в 2 ) называется неполным квадратом суммы.
5. Многочлен вида (а 2 -ав+в 2 ) называется неполным квадратом разности.
2. Историческая справка
Некоторые правила сокращённого умножения были известны ещё около 4 тыс. лет тому назад. Их знали вавилоняне и другие народы древности. Тогда они формулировались словесно или геометрически.
Например, тождество (a+b) 2 =a 2 +2ab+b 2
Доказательство опиралось на геометрические соображения:
Некоторые термины такого геометрического изложения алгебры сохранились до сих пор. Так, мы называем вторую степень числа квадратом, а третью степень - кубом числа.
3. Формулы сокращенного умножения, изучаемые в школе
Математиками было подмечено, что некоторые многочлены можно умножать короче, быстрее, чем остальные. Так появились ФСУ. Несколько формул изучается по школьной программе. Рассмотрим их:
(a+b) 2 =a 2 +2ab+b 2
(a-b) 2 =a 2 -2ab+b 2
(a+b) 3 =a 3 +3a 2 b+3ab 2 +b 3
(a-b) 3 =a 3 -3a 2 b+3ab 2 -b 3
a 3 +b 3 =(a+b)(a 2 -ab+b 2 )
a 3 - b 3 = (a - b)(a 2 +ab+b 2 )
Все эти формулы доказываются непосредственным раскрытием скобок и приведением подобных слагаемых. Они остаются справедливыми, если в них вместо a и b подставить любые целые выражения.
Например докажем формулу a 3 +b 3 = ( a + b )( a 2 – ab + b 2 ).
Имеем: ( a + b )( a 2 – ab + b 2 ) = a 3 – a 2 b + ab 2 + ba 2 – ab 2 – b 3
Приводя подобные слагаемые, мы видим, что
(a + b)(a 2 – ab + b 2 ) = a 3 +b 3 , что и доказывает нужную формулу.
4. Формулы сокращенного умножения, не изучаемые по школьной программе
4.1. Треугольник Паскаля
Блез Паскаль (1623— 1662).
Исаак Ньютон (1643—1727).
Из дополнительной литературы я узнал, что многие ФСУ являются частным случаем Бинома Ньютона.
Запомнить такую формулу непросто.
Построим треугольник Паскаля для (a+b) n :
n=5 1 5 10 10 5 1
n=6 1 6 15 20 15 6 1
n=7 1 7 21 35 35 21 7 1
n=8 1 8 28 56 70 56 28 8 1
n=9 1 9 36 84 126 126 84 36 9 1
n=10 1 10 45 120 210 252 210 120 45 10 1
Некоторые историки науки приписывают Блезу Паскалю авторство не только треугольника, позволяющего находить биномиальные коэффициенты, но и самой формулы бинома. Они считают, что Паскаль вывел её несколько раньше Ньютона, а тот лишь обобщил формулу для разных показателей степеней.
Творческая работа учащихся 7 класса.В курсе алгебры 7 класса изучаются формулы сокращенного умножения, которые доказываются с помощью алгебраических преобразований. Мы задались целью узнать о формулах сокращенного умножения больше и доказать их используя геометрические свойства фигур.
| Вложение | Размер |
|---|---|
| geometricheskoe_dokazatelstvo_formul_sokrashchennogo_umnozheniya.docx | 799.48 КБ |
Предварительный просмотр:
Муниципальное образовательное учреждение
средняя общеобразовательная школа №48 Ворошиловского района Волгограда
Геометрическое доказательство формул сокращенного умножения
Дорожкина Юлия и
Фирсова Ирина Юрьевна
Глава 1. Исторические сведения
Глава 2. Формулы школьного курса математики
1.1 Алгебраическое представление формул сокращенного умножения
1.2 Геометрическое доказательство формул сокращенного умножения
Глава 3. Возведение в квадрат суммы нескольких слагаемых
Глава 4. Треугольник Паскаля
Тема исследования: Геометрическое доказательство формул сокращенного умножения
Предмет исследования: Формулы сокращенного умножения.
Цель: доказать формулы сокращенного умножения, используя геометрические приемы; рассмотреть вопрос о существовании других формул сокращенного умножения, которые не рассматриваются в школьной программе
Глава 1. Исторические сведения
Найденные древневавилонские клинописные тексты свидетельствуют, что формулы сокращённого умножения были известны около 4000лет назад. Их знали, кроме вавилонян, и другие народы древности, конечно, не в нашем символическом виде, а словесно или в геометрической форме, как у древних греков.

В дальнейшем мы приведем пример такого доказательства.

Первым ученым, который отказался от геометрических способов выражения и перешел к алгебраическим уравнениям был древнегреческий ученый-математик Диофант , живший в 3 веке до нашей эры .А формулыполучили название формулы сокращенного умножения .
( III век н. э.) — древнегреческий математик.

(a + b)² = a² + 2ab +b² ( 1 )
(a – b)² = a² - 2ab + b² ( 2 )
(a + b)³ = a³ + 3a²b + 3ab² + b³ ( 3 )
(a –b)³ = a³ - 3a²b + 3ab² - b³ ( 4 )
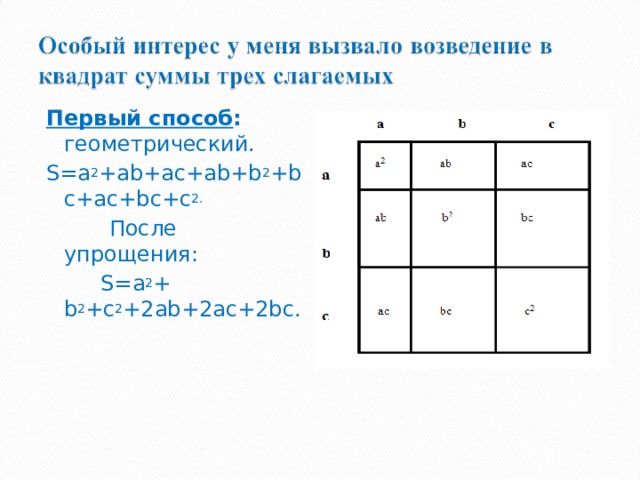
Первый способ : геометрический.
S = a 2 + ab + ac + ab + b 2 + bc + ac + bc + c 2.
S=a 2 + b 2 +c 2 +2ab+2ac+2bc.

Второй способ : алгебраическое умножение многочленов.
(a+b+c)*(a+b+c)=a 2 +ab+ac+ab+b 2 +bc+ac+bc+c 2 = = a 2 + b 2 +c 2 +2ab+2ac+2bc.
Третий способ : как сумма двух слагаемых в квадрате
(( a + b )+ c ) 2 =( a + b ) 2 +2( a + b ) c + c 2 = a 2 + c 2 + b 2 +2 ab +2 ac +2 bc .

(a+b+c) 2 =a 2 +c 2 +b 2 +2ab+2ac+2bc

Я предположил, что в квадрат можно возвести сумму нескольких слагаемых. Подтверждение этому я нашёл в справочной литературе:
(a 1 + a 2 + …+ a п )² =
a 1 ²+ a 2 ²+…+2(a 1 a 2 +a 1 a 3 +…+a i a j +…+a n-1 a.)

1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
Решить уравнение:
(x – 6) 2 – x(x + 8) = 2
x(x – 1) – (x – 5) 2 = 2
x 2 -12x + 36 – x 2 – 8x = 2 – 20x + 36 = 2 – 20x = 2 – 36 – 20x = – 34 x = 1,7
x 2 – x – (x 2 – 10x+25) = 2 x 2 – x – x 2 + 10x – 25 = 2 9x – 25 = 2 9x = 27 x = 3
Мне очень нравится предмет математика.
Она учит точности мысли, логике, умению делать обобщения.
Я считаю, что те знания, которые я приобрел, пригодятся мне в дальнейшей учебе и подготовке к выпускным экзаменам.


-75%
Читайте также:

