Функциональное описание реальных процессов реферат

Обновлено: 01.07.2024

Социальные изменения в обществе протекают в результате целенаправленной деятельности людей, которая состоит из отдельных социальных действий и взаимодействий. Как правило, разрозненные действия редко могут привести к значительным социальным и культурным изменениям. Даже если один человек сделал великое открытие, множество людей должны использовать его, внедрить в свою практику. Таким образом, значительные социальные изменения происходят в процессе совместных действий людей, которые не разрознены, а, наоборот, однонаправлены, взаимно сопряжены. Причем это сопряженность часто может быть бессознательным благодаря наличию у людей мотивов и ориентаций. Таким образом общество представляет собой не статичную субстанцию, а совокупность постоянных изменений как элементов, так и взаимодействий между ними, внутри которых протекают различные социальные процессы.

Цель данной работы раскрыть тему: функционирование и развитие как базовые социальные процессы. Для этого необходимо рассмотреть сущность социальных отношений, так как они определяют социальную структуру общества, его качественную определенность, и критерии функционирования и развития.

социальный процесс функционирование развитие

Классическое определение социального процесса дал Питирим Сорокин: “Под процессом понимается любой вид движения, модификации, трансформации, чередования или “эволюции”, короче говоря, любое изменение данного изучаемого объекта в течение определенного времени, будь то изменение его места в пространстве, либо модификация его количественных и качественных характеристик”.

Под процессом понимается любой вид движения, смены состояний какого - либо объекта или явления. Это бесконечный поток событий, модификаций, трансформаций, социокультурных изменений. Эта так же последовательность социальных событий. Без процесса, приводящего к тем или иным изменениям, социальная система существовать не может. Изменения - это результат различных процессов, происходящих в течение определенного времени.

Процессы происходят на различных уровнях социальной системы. Объектом наблюдения может быть отдельный индивид, социальная группа, организация, общество, все человеческое общество.

Наряду с реально протекающими процессами и происходящими изменениями в человеческом сознании происходят процессы осмысления, оценки, переоценки и интерпретации тех или иных событий. При этом точек зрения на одно и то же событие может быть бесконечное множество, от частично совпадающих до прямо противоположных. Так, большевики и многие миллионы людей в СССР и во всем мире оценивали и продолжают оценивать Октябрьскую революцию 1917 г. как высочайшее прогрессивное событие в истории человечества, а значительная часть человечества, в том числе и России, - как величайшую трагедию российского (и не только) народа. Кроме того, человеческому сознанию свойственно постоянно переоценивать уже случившееся и давать прошедшим событиям новые толкования. Таким образом происходит конструирование в сознании людей новой социальной реальности [5, c.84].

Социальные процессы есть следствие связи и взаимодействия следующих структурных элементов:

1) субъектов (государства, политических партий, общественных организаций и движений и т.д.);

2) объективных условий (общественной системы, окружающей среды, вещественной среды): экономические и общественно-политические условия, производственно-технические и технологические условия труда, производственно-бытовые и материально-бытовые условия, возможности реализации свободного времени, система образования, жилищные и культурно-бытовые условия, социально-психологический климат в обществе, в трудовых ассоциациях, демографическая ситуация и др.;

3) субъективных условий (способностей людей воздействовать (или нет) на те или иные социальные процессы);

4) потребностей и интересов субъектов относительно тех или иных процессов (например, смены форм собственности, участия в политических и других общественных преобразованиях и т.д.).

Социальные процессы различают по объекту (человечество, общество, класс, организация, малая группа и т.д.), по степени управления (стихийный процесс, естественно-исторический, целенаправленный). С учетом того, что социальный процесс может рассматриваться не только в узком смысле (как изменения в социальной сфере, в социальных отношениях), но и в широком, можно выделить социокультурные, индустриально-технологические и социально-экономические. Следует также обратить внимание на отличие социальных процессов от экономических, политических и других общественных процессов, которое обусловлено тем, что субъектом движения здесь является социальное качество человека и общества. Своеобразие социальных процессов состоит в том, что они пронизывают все другие процессы общественной жизни, так как изменение личности, класса, семьи, других социальных групп пронизывает все стороны их жизнедеятельности [6, c.54].

В литературе приводится различная классификация социальных процессов. Это объясняется тем, что используются разные основания классификации: степень общности, качество, длительность протекания, причинная обусловленность, иерархичность структуры, сферы проявления и т.д. Социальные процессы можно также дифференцировать по субъекту, по целям и результатам. Так, различают социальные процессы функционирования, обеспечивающие воспроизводство качественного состояния объекта, социальные процессы развития, обусловливающие переход объекта к качественно новому состоянию; при этом развитие может быть прогрессивным и регрессивным, эволюционным и революционным [6, c.56].

Функционирование - в его рамках структуры и институты изменяются так, что их основные параметры не выходят за рамки общепринятых базовых значений и показателей и имеют адаптивный характер. Функциональные изменения можно сравнить с профилактическим обслуживанием и текущим ремонтом автомобиля. Такие "ремонты" проводятся для поддержания системы в "рабочем состоянии". В задачу функциональных изменений не входят радикальные реформы, предлагающие качественные структурные преобразования. Их цель - приспособление к меняющимся условиям окружающей среды (природной и социальной) и внутренним потребностям социальной системы [5, с.86].

Развитие - в этом случае происходит изменение базовых параметров экономических и политических систем и институтов. Считается, что эти изменения должны вести к положительным последствиям для их систем (экономический рост, рост уровня благосостояния населения, экономические и политические процессы, развитие многопартийности, открытости государственных институтов).

Социальное развитие - это форма, раскрывающая потенциал, который изначально заложен в системе. Речь в данном случае идет о направленном процессе, т.е. таком, в котором ни одно из состояний системы не повторяется ни на какой предыдущей стадии, а на более поздней выходит на более высокий уровень в какой-либо сфере (например, рост экономических показателей, продвинутость технологий или увеличение населения). Кроме того, система последовательно приближается к некому всеобщему состоянию (например, общество приближается к состоянию социального равенства, процветания или демократического представительства), причем это стимулируется имманентными свойствами самой системы (внутренние противоречия разрешаются благодаря появлению качественно новых форм социальной жизни; присущее людям творческое начало направляется на масштабные организационные инновации и т.д.).

Структура социального объекта обеспечивает необходимую устойчивость в функционировании взаимосвязанных элементов, позволяющую накапливать количественные изменения вплоть до момента, когда наступает историческая необходимость структурных сдвигов в обществе.

Целостные социальные системы динамичны, что означает, что в них протекают процессы, т.е. имеет место изменение структурных элементов и связей между ними, которое постепенно переводит систему из одного состояния в другое. Целое представляет собой процесс, а поэтому структура является организацией его во времени.

Социальная структура охватывает размещение всех отношений, зависимостей, взаимодействий между отдельными элементами в социальных системах разного ранга сдвигов в обществе. Относительный консерватизм социальной структуры выступает как момент динамизма общественных процессов в целом [3, c.141].

Почти за два столетия социология выработала достаточно много концепций, моделей и теорий, связанных с социальными изменениями.

Социальные изменения, включая широкомасштабные исторические преобразования, не происходят стохастически, не предрешены проведением. Он являются результатом действий ряда сил - агентов социальных изменений. Ими могут быть люди, идеи или процессы, который в силу конкретных обстоятельств меняют ход человеческой истории, а вместе с ней - судьбы миллионов людей.

Важным критерием социальных процессов является конечный результат. В его основе лежат противоречия, возникающие между различными социальными группами, располагающими особыми корпоративными интересами, входящими в несоответствие с интересами других групп. Такое положение является абсолютно естественным и позволяет обществу находить наиболее эффективный путь развития, способный консолидировать интересы большинства своих членов.

Социальные процессы привнося в жизни общества как позитивные для большинства людей результаты, так и негативные. Вследствие этого возникающие в обществе проблемы вызывают изменения, от которых одни категории людей получают пользу, тогда как другие терпят ущерб. Сами люди, являясь непосредственными участниками социальных процессов, тем не менее, не всегда в состоянии оказывать на них влияние. Причина этого заключается в том, что, вызывая соответствующие изменения в обществе, люди утрачивают контроль над ними в силу неготовности или неспособности понять внутренние механизмы этих изменений.

Так, например функционирование, как социальный процесс, имеет адаптивный характер по отношению к социуму, а развитие раскрывает потенциал, который изначально заложен в системе.

1. Горбунова М.Ю. Общая социология. Конспект лекций. - М.: Эксмо, 2008. - 160 с.

2. Забродин В.Ю. Социология. Экзаменационные ответы для студентов вузов. Издательство: Питер, 2009. - 160 с.

3. Захаров М.А. Социология: курс лекций - Смоленск: СмолГУ, 2007. - 168с.

4. Здравомыслов А.Г., Лапин Н.И. Общая социология. Хрестоматия - М.: "Высшая школа", 2006. - 783 с.

5. Козырев Г.И. Основы социологии и политологии: учебник. - М.: ФОРУМ: ИНФРА - М, 2008. - 204 с.

6. Павленюк П.Д., Куканова Е.В. Основы социологии и политологии: учебное пособие - М.: ФОРУМ: ИНФРА - М, 2007. - 272 с.

7. Ритерман Т.П. Социология: Полный курс - М.: АСТ, 2009. - 128 с.

8. Рой О.М., Киселева А.М. Исследование социально-экономических и политических процессов - СПб.: Питер, 2007. - 240 с.

9. Тавокин Е.П. Исследование социально-экономических и политических процессов: учебное пособие - М.: ИНФРА-М, 2009. - 188 с.

Почему не бывает животных, какой угодно величины? Почему, например, нет слонов в три раза большего роста, чем существуют, но тех же пропорций? Наш ответ таков: стань слон в три раза больше, вес его тогда увеличился бы в двадцать семь раз, как куб размера, а площадь сечения костей и, следовательно, их прочность — только в девять раз, как квадрат размера. Прочности костей уже не хватило бы, чтобы выдержать непомерно увеличившийся вес. Такой слон был бы раздавлен собственной тяжестью.

В основу рассуждения положены две строгие математические зависимости. Первая устанавливает соответствие между разме¬рами подобных тел и их объемами: объем изменяется, как куб размера. Вторая связывает размеры подобных фигур и их площади: площадь изменяется, как квадрат размера. Этим выразительным примером мы хотим начать разговор о числовых функциях числового аргумента, которые можно использовать для описания реальных процессов.

Чудо английского часового мастера Джон Гаррисон.

Перенесемся на три века вспять. Парусник в открытом море. Как определить долготу места, в котором он находится? Очень просто, если на корабле есть часы, поставленные в порту отправления. Нужно измерить местное время по солнцу и сравнить с показаниями часов. Расхождение пропорционально разнице по долготе между тем пунктом, где находится корабль, и тем, в котором были поставлены часы.

Точный закон этой пропорциональности позволяет вывести простое соотношение: тремстам шестидесяти градусам земной окружности соответствуют двадцать четыре часа, за которые Земля совершает полный оборот вокруг своей оси. Поэтому если часы отстают по сравнению с местным временем на шесть часов, корабль находится на 90° восточнее того места, где были поставлены часы. Спешат на четыре часа — на 60° западнее. Разумеется, для подобного определения долготы нужны очень точные часы.

А как можно требовать точности от маятниковых часов, которыми снабжен парусник? Их ход зависит от длины маятника, а она то и дело меняется: теплый день сменяется прохладной ночью, и во время плавания парусник приближается то к голубым полярным льдам, то к пальмам тропиков. Тепло удлиняет маятник, холод укорачивает. Такова неумолимая реальность.

И все-таки нашелся способ избежать неизбежного зла. Чудо совершил в 1726 году английский часовой мастер Джон Гаррисон. Это удалось ему потому, что он знал функциональную зависимость длины металлического стержня от температуры, до которой стержень нагрет.

Эту функцию описывает прямая линия. Такая зависимость называется линейной. Суть ее в том, что одинаковым приращениям аргумента всегда соответствует одно и то же приращение функции. Иначе говоря, функция изменяется равномерно при равномерном росте аргумента.

В нашем примере равномерному нарастанию температуры соответствует равномерное удлинение стержня. Полное его удлинение пропорционально начальной длине. Но что особенно важно — стержни из разных металлов удлиняются по-разному от одного и того же прироста температуры. Скажем, цинк расширяется примерно в три раза сильнее, чем сталь, этим и воспользовался Гаррисон: он собрал маятник из цинковых и стальных стержней. Общая длина стальных стержней в три раза превышала длину цинковых. Расширяясь при нагревании и сокращаясь при охлаждении, стержни взаимно компенсировали изменения своей длины, и груз маятника оставался на одном и том же расстоянии от точки подвеса.

Ключ к небольшой математической проблеме

Отметим, что не всякую функциональную зависимость удается выразить краткой формулой, мы не случайно в качестве примера предоставляем вам, ключ от дверного замка: сейчас он в буквальном смысле слова послужит ключом к небольшой математической проблеме, к которой нас подводит беседа о функциях. Знаете ли вы, как таким ключом открывается дверной замок? Что происходит внутри этого слесарно-механического устройства, когда вы вставляете ключ в замочную скважину и делаете положенное число оборотов?

Чтобы замок открылся, нужно провернуть барабан, в котором сделана скважина. Но этому препятствуют штифты, стоящие тесным строем внутри скважины, скользящие вверх-вниз. Каждый из штифтов нужно поднять на такую высоту, чтобы их верхние торцы оказались вровень с поверхностью барабана. Если они выступят за нее, то войдут в прорезь обоймы, расположенную точно над заочной скважиной; если не достигнут поверхности барабана, то из прорези обоймы находящиеся там штифты вдвинутся в замочную скважину. И в том и в другом случае вращение барабана будет застопорено.

Штифты в замочной скважине поднимает ключ, вдвигаемый в нее. При этом высота каждого штифта, будучи сложена с высотой профиля ключа в соответствующей точке, должна дать в сумме диаметр барабана. Только тогда он провернется.

Ну а причем здесь функция? Да притом, что, с точки зрения математика, вся эта механика есть не что иное, как операция сложения двух функций. Одна из них — это профиль ключа. Другая — линия, очерчивающая верхние торцы штифтов, когда замок заперт.

Золотое правило механики

Вся богатейшая семья механизмов, окружающих современного человека, начиналась когда-то с семи простых машин. Древние знали рычаг, блок, клин, ворот, винт, наклонную плоскость и зубчатые колеса. Эти нехитрые по теперешним представлениям устройства умножали силу человека. Но, во сколько раз выиграешь в силе — во столько же раз проиграешь в расстоянии. Так гласит золотое правило механики, заключающее в себе теорию семи простых машин.

График, приведенный на этой странице, есть наглядное выражение знаменитого правила. По горизонтальной оси отложена сила, с которой, например, нужно давить на плечо рычага, чтобы поднять заданный груз на заданную высоту. По вертикальной оси — расстояние, которое пройдет при этом точка приложения силы. Линия, выражающая такую функциональную зависимость, называется гиперболой.

Закон обратной пропорциональности глядит на нас и со шкалы радиоприемника. Вы крутите ручку настройки, и стрелка движется вдоль шкалы, на которой два ряда чисел — метры и мегагерцы, длина волн и их частота. Длина волн растет, частота падает. Но присмотритесь: при любом сдвиге стрелки во сколько раз увеличилась длина волны, во столько же раз упала частота.

График гиперболы можно увидеть на лабораторном столе физика, демонстрирующего явления капиллярности. В штативе несколько тонких стеклянных трубочек, расположенных в порядке возрастания диаметров. Известно, что в тонком канале смачивающая жидкость поднимается тем выше, чем меньше его диаметр. Поэтому в самом узком канале жидкость поднялась выше всего, в другом канале, диаметр которого в два раза больше, — в два раза ниже, в третьем, что толще первого в три раза,— в три раза ниже и так далее.

А теперь опустим в эту же жидкость клин, образованный двумя стеклянными пластинками, сомкнутыми по вертикальному ребру. В узкую щель между стеклами жидкость устремится, как в капилляр. Высота ее подъема определится шириной зазора. А он увеличивается равномерно по мере удаления от острия клина. Поэтому свободная поверхность жидкости четко вырисовывает гиперболу — график обратной пропорциональности.

Информационный бум

Сейчас много говорят об информационном буме. Поток информации захлестывает: утверждают, что ее количество удваивается каждые десять лет. Изобразим этот процесс наглядно, в виде графика некоторой функции.

Примем объем информации в некоторый год за единицу. Поскольку эта величина послужит нам началом дальнейших построений, отложим ее над началом координат, в которых будет строиться график, по вертикальной оси. Отрезок, вдвое больший, восставим над единичой отметкой горизонтальной оси, считая, что эта отметка соответствует первому десятку лет.

А что если посмотреть, как нарастал поток информации до того года, который принят за начальный? Столь же равномерно, откладывая единицу за единицей, пройдемся по оси абсцисс влево от начала координат и над отложенными значениями аргумента, будем наносить на график значения функции уже в порядке убывания — вдвое с каждым шагом.

Звездный график

Сколько звезд на небе? Одним из первых, кто попытался точно ответить на этот вопрос, был древнегреческий астроном Гиппарх. При его жизни в созвездии Скорпиона вспыхнула новая звезда. Гиппарх был потрясен: звезды смертны, они, как люди, рождаются и умирают. И чтобы будущие исследователи могли следить за возникновением и угасанием звезд, Гиппарх составил свой звездный каталог. Он насчитал около тысячи звезд и разбил их по видимому блеску на шесть групп. Самые яркие Гиппарх назвал звездами первой величины, заметно менее яркие — второй, еще столь же менее яркие — третьей и так далее в порядке равномерного убывания видимого блеска — до звезд, едва ви¬димых невооруженным глазом, которым была присвоена шестая величина.

Именно в силу описанной физиологической особенности звезды, ярко горящие на ночном небе, не видны днем, тонут в ослепительном блеске солнца, рассеянном по небосводу. И там и здесь сияние звезд дает одну и ту же добавку к свету фона. Однако в первом случае (ночью) эта добавка велика по сравнению с мерцанием неба, во втором же (днем) составляет весьма незначительную долю от солнечного блеска (менее чем миллиардную даже для самых ярких звезд). Оттого же и голос солиста, когда его пение подхватывает хор, тонет в многоголосом звучании. Суть функциональной зависимости, описанной нами на примере зрения и слуха, в том, что возрастанию аргумента в одно и то же число раз всегда соответствует оно и то же приращение функции. Когда аргумент меняется по закону геометрической прогрессии, функция меняется по закону арифметической прогрессии.

Современная математика знает множество функций, и у каждой свой неповторимый облик, как неповторим облик каждого из миллиардов людей, живущих на Земле. Однако при всей непохожести одного человека на другого у каждого есть руки и голова, уши и рот. Точно так же облик каждой функции можно представить сложенным из набора характерных деталей. В них проявляются основные свойства функций.

Функции — это математические портреты устойчивых закономерностей, познаваемых человеком. Чтобы проиллюстрировать характерные свойства функций, нам показалось естественным обратиться к пословицам. Ведь пословицы — это тоже отражение устойчивых закономерностей, выверенное многовековым опытом народа.

Обе функции, зависящие от времени, возрастающие. Но, как видно, расти можно по-разному. Наклон одной кривой постоянно увеличивается. Рост функции усиливается с ростом аргумента. Такое свойство функции называется вогнутостью.

Наклон другой кривой неизменно уменьшается. Рост функции слабеет с ростом аргумента. Такое свойство функции называется выпуклостью.

Нетрудно найти иллюстрации этим понятиям и среди элементарных функций. Показательная функция – вогнутая. Логарифм, корень квадратный – выпуклые. Выпуклую параболу выписывает и снаряд, выпущенный из пушки под углом к горизонту. Вогнутой функцией является гипербола, построенная для положительных значений аргумента. Другая ветвь гиперболы выпуклая.

Математические категории, о которых шла речь, естественным образом делятся на две группы. Одни описывают поведение функции в окрестности некоторых характерных точек (максимум, минимум, перегиб). Другие описывают поведение функции в некоторых промежутках (выпуклость, вогнутость, убывание, возрастание).

Теория реальных газов

Физикам важно знать, как ведут себя газы при различных температурах и давлениях. Поведение газа определяется взаимодействием между его молекулами. Предположим для простоты, как это часто делается в физике, что молекулы — это маленькие упругие шарики. Рассмотрим две такие молекулы, и будем изучать, какому закону подчиняется сила их взаимодействия.

Известно, что на больших расстояниях молекулы взаимно притягиваются, причем с ростом расстояния сила притяжения убывает, стремясь к нулю. При сближении молекул она, напротив, возрастает. Когда шарики сближаются до соприкосновения, в игру вступает еще одна, противоположно направленная сила — сила упругого отталкивания. Она тем больше, чем сильнее прижаты шарики друг к другу, чем меньше расстояние между их центрами. Гипотетически можно представить центры моле¬кул сближающимися на сколь угодно малое расстояние, отчего сила их взаимного отталкивания возросла бы неограниченно.

Над дальним концом положительной полуоси абсцисс проведем прилегающий к ней вогнутый штришок. Своей близостью к горизонтальной оси он покажет, что с удалением молекул друг от друга сила их взаимодействия убывает до нуля, а вогнутой формой — что при сближении молекул сила их взаимного притяжения возрастает все круче. В точке с абсциссой, равной удвоенному радиусу молекулы, на условной высоте отметим точку перегиба; в этой точке силы упругого отталкивания, вступив в игру, заставляют кривую графика сменить свое прежнее, все более крутое возрастание на возрастание все более замедляющееся.

В точке с абсциссой, еще меньшей, на чуть большей высоте проведем дужку выпуклостью кверху. Она означает, что сила взаимодействия достигла максимума: с дальнейшим уменьшением аргумента силы упругого отталкивания преобладают над силами притяжения, кривая устремляется вниз. Выпуклый отвесный штрих проведем у нижнего конца оси ординат, чуть правее от него. Эта деталь показывает, что сила отталкивания между молекулами неограниченно возрастает, когда их центры неограниченно сближаются.

Поскольку сила взаимодействия между молекулами определена для любого расстояния между их центрами, график должен быть непрерывной линией. Соединим намеченные штрихи гладкой кривой. Такую картину часто можно увидеть в книгах по физике, правда, в перевернутом виде; у физиков сложилась традиция трактовать силы притяжения как отрицательные величины, силы отталкивания – как положительные.

Взаимно обратные функции

Космодром. Ракета, летящая в космическом пространстве, наращивает скорость по закону логарифма: именно эта функция позволяет по массе израсходованного топлива указать скорость ракеты. Скорость — функция, масса топлива — аргумент. Но часто возникает обратная задача, когда исходным пунктом расчета является скорость ракеты. Чтобы вывести спутник на орбиту, ракета должна развить первую космическую скорость. Какое количество топлива потребуется ракете, чтобы достичь назначенной скорости? Масса топлива в этом вопросе уже мыслится как функция, скорость — как аргумент. Задачу решает функция, обратная к логарифмической функции, — показательная.

Функция логарифмическая и функция показательная. Сведем их на одном графике. Бросается в глаза: они расположены симметрично относительно биссектрисы угла, стороны которого - оси координат. Это не удивительно — ведь переход от прямой функции к обратной заключается в переименовании: функция становится аргументом, аргумент — функцией. Заметим, что функция, обратная линейной, - это опять-таки линейная функция. Квадратный корень и парабола тоже являются взаимно обратными функциями, и графики их тоже симметричны относительно той же биссектрисы.

Какие свойства функции гарантируют то, что обратная к ней окажется однозначной? Эти свойства – непрерывность и монотонность. Линейная и показательная функции, парабола и корень квадратный – каждая из них непрерывна в любой точке своей области существования. Неразрывна всюду, как говорят в таких случаях. Прекрасные примеры всюду непрерывных функций дают процессы движения. Причина в том, что пространство и время непрерывны.

Для учеников 1-11 классов и дошкольников
Бесплатные сертификаты учителям и участникам

Функциональное описание реальных процессов

В основу рассуждения положены две строгие математические зависимости. Первая устанавливает соответствие между размерами подобных тел и их объемами: объем изменяется, как куб размера. Вторая связывает размеры подобных фигур и их площади: площадь изменяется, как квадрат размера. Этим выразительным примером мы хотим начать разговор о числовых функциях числового аргумента, которые можно использовать для описания реальных процессов.

Чудо английского часового мастера Джон Гаррисон.

Ключ к небольшой математической проблеме

Операция сложения функций состоит в том, что в каждой точке из общей области их определения к значению одной функции прибавляется значение другой. Тем самым определяется, какое значение в данной точке имеет функция, называемая суммой двух исходных. Секрет дверного замка в том, что в результате сложения двух функций, выраженных профилем ключа и строем штифтов, получается функция-константа, постоянное значение которой равно диаметру барабана

Золотое правило механики

Информационный бум

Примем объем информации в некоторый год за единицу. Поскольку эта величина послужит нам началом дальнейших построений, отложим ее над началом координат, в которых будет строиться график, по вертикальной оси. Отрезок, вдвое больший, восставим над единичной отметкой горизонтальной оси, считая, что эта отметка соответствует первому десятку лет.

Теперь соединим все нанесенные точки непрерывной гладкой линией — ведь количество информации нарастает от десятилетия к десятилетию плавно, а не скачками. Перед нами график так называемой показательной функции.

Звездный график

Сколько звезд на небе? Одним из первых, кто попытался точно ответить на этот вопрос, был древнегреческий астроном Гиппарх. При его жизни в созвездии Скорпиона вспыхнула новая звезда. Гиппарх был потрясен: звезды смертны, они, как люди, рождаются и умирают. И чтобы будущие исследователи могли следить за возникновением и угасанием звезд, Гиппарх составил свой звездный каталог. Он насчитал около тысячи звезд и разбил их по видимому блеску на шесть групп. Самые яркие Гиппарх назвал звездами первой величины, заметно менее яркие — второй, еще столь же менее яркие — третьей и так далее в порядке равномерного убывания видимого блеска — до звезд, едва видимых невооруженным глазом, которым была присвоена шестая величина.

Именно в силу описанной физиологической особенности звезды, ярко горящие на ночном небе, не видны днем, тонут в ослепительном блеске солнца, рассеянном по небосводу. И там и здесь сияние звезд дает одну и ту же добавку к свету фона. Однако в первом случае (ночью) эта добавка велика по сравнению с мерцанием неба, во втором же (днем) составляет весьма незначительную долю от солнечного блеска (менее чем миллиардную даже для самых ярких звезд). Оттого же и голос солиста, когда его пение подхватывает хор, тонет в многоголосом звучании.Суть функциональной зависимости, описанной нами на примере зрения и слуха, в том, что возрастанию аргумента в одно и то же число раз всегда соответствует оно и то же приращение функции. Когда аргумент меняется по закону геометрической прогрессии, функция меняется по закону арифметической прогрессии.

Как же называется функция, с которой мы познакомились по звездному небу? Ординаты выделенных точек графика являются логарифмами абсцисс, взятых по основанию 2,5 . Такую функцию называют логарифмической.

Математические портреты пословиц

Теория реальных газов

Известно, что на больших расстояниях молекулы взаимно притягиваются, причем с ростом расстояния сила притяжения убывает, стремясь к нулю. При сближении молекул она, напротив, возрастает. Когда шарики сближаются до соприкосновения, в игру вступает еще одна, противоположно направленная сила — сила упругого отталкивания. Она тем больше, чем сильнее прижаты шарики друг к другу, чем меньше расстояние между их центрами. Гипотетически можно представить центры молекул сближающимися на сколь угодно малое расстояние, отчего сила их взаимного отталкивания возросла бы неограниченно.

Взаимно обратные функции

ПЗ № 17. Примеры зависимостей между переменными в реальных процессах из смежных дисциплин. Определение функций.

1) Опорный конспект.

А) Примеры применения различных функций в жизни, технике, природе.

Определение. Числовой функцией с областью определения D называется соответствие, при котором каждому числу x из множества D сопоставляется по некоторому правилу единственное число y, зависящее от x. Принято называтьx независимой переменной или аргументом, а у — зависимой переменной или значением функции.

Записывают указанное соотношение между x и у в общем виде так: у = f (x) или у = F (x) и т. п.

График функции y = f (х) - это множество всех точек плоскости, координаты (х, у) которых удовлетворяют соотношению y = f(x).

Способы задания функции:

1) аналитический (с помощью формулы);

а) Линейная функция

Функция y = a x + b называется линейной потому, что ее график есть прямая линия. Характеристическим свойством линейной функции является изменение функции пропорционально изменению аргумента. Поэтому с помощью линейной функции описываются пропорциональные зависимости. Например, при равномерном движении с постоянной скоростью v пройденный путь s пропорционален времени t и выражается формулой s = v t, т.е. s – линейная функция t.

Пример линейной функции дает зависимость между различными шкалами температур. Абсолютная температура Т (по Кельвину) связана с температурой t ͦ C на шкале Цельсия формулой t = T + 273 ͦ . Другой пример – напряжение в электрической цепи прямо пропорционально силе тока U = IR . Можно много приводить примеров линейных зависимостей в физике, химии. Рассмотрим задачу на линейное расширение тел.

Задача. При температуре 0 о С рельс имеет длину l₀= 12,5 м. при возрастании температуры происходит тепловое расширение рельса и его длина, выраженная в метрах, меняется по закону l(t о ) = l₀(1 + t о ),где = 1,2 ˖ 10 –5 – коэффициент теплового расширения в градусах Цельсия в минус первой степени, t о – температура (в градусах Цельсия). При какой температуре рельс удлинится на 6 мм. Ответ выразить в градусах Цельсия.

Решение. Выразим из заданной формулы t : .

Заметим, ,

тогда

б) Квадратичная функция

Графиком квадратичной функции

является парабола.

Хорошо известно, что траектория камня, брошенного под углом к горизонту, летящего футбольного мяча или артиллерийского снаряда будет параболой (при отсутствии сопротивления воздуха). Однако мало кто знает, что зона достижимости для пущенных нами камней вновь будет параболой. В данном случае мы говорим об огибающей кривой траекторией камней, выпущенных из данной точки под разными углами, но с одной и той же начальной скоростью. Если рассматривать такую огибающую в пространстве, то возникнет поверхность, образованная вращением этой параболы вокруг ее оси. Такая поверхность носит название параболоида вращения.

Задача. Высота над замлей подброшенного вверх мяча меняется по закону , где h — высота в метрах, t — время в секундах, прошедшее c момента броска. Сколько секунд мяч будет находиться на высоте не менее трёх метров?

Решение. Решим неравенство ,

, , t ₁ = 1,4, t ₂ = 0,2

0,2 ≤ t ≤ 1,4

t = 1,4 - 0,2 = 1,2

Парабола обладает оптическим свойством: все лучи, исходящие из источника света, находящегося в фокусе параболы, после отражения оказываются направленными параллельно ее оси. Это свойство параболы используется при изготовлении прожекторов, автомобильных фар, карманных фонариков, зеркала которых имеют вид параболоидов вращения.

Б)Функциональные зависимости в повседневной жизни

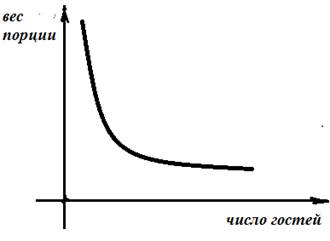
Пример 1. Рассмотрим деление праздничного торта между гостями. Отчего зависит количество порций?– от числа гостей. А от чего зависит вес порции? – тоже от числа гостей.

− В первом случае, чем больше гостей, тем на большее количество порций мы должны разделить торт (рис. 1).

Здесь наглядно можно представить прямую пропорциональную зависимость.

Во втором случае, чем больше гостей, тем меньше вес порции. Здесь мы видим обратную пропорциональную зависимость (рис. 2).

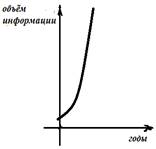
Пример 2. Мы живём в век информационных технологий. Ежедневно мы получаем массу информации из различных источников: телевидения, радио, газет, журналов, и, конечно, из Интернета. Известно, что объём информации каждые пять лет увеличивается в два раза.

Если построить график зависимости объёма информации от времени, то получим некоторую кривую, которая в математике называется экспонентой и является графиком показательной функции (рис. 3).

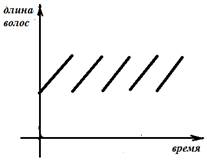
Пример 3. На голове человека растут волосы, которые регулярно стригут.

График полученной зависимости (при условии, что стрижку делают регулярно) похож на функцию дробной части числа, смещённую на a единиц вверх: (рис. 4).

Пример 4 . За время обучения в школе каждый год переходим в следующий класс.

Такая зависимость сходна с функцией целой части числа на ограниченном промежутке (рис. 5).

Читайте также: