Запишите уравнение равномерного поступательного движения твердого тела кратко

Обновлено: 04.07.2024

22. Кинематика твердого тела. Поступательное движение твердого тела.

Для тех задач кинематики, где геометрическими размерами тел пренебречь нельзя, необходимо рассматривать движение механических тел с учетом их геометрических размеров.

Студенты технологи изучают три вида движения твердого тела, А именно, поступательное движение твердого тела, вращательное движение твердого тела вокруг неподвижной оси и плоскопараллельное (плоское) движение твердого тела.

Поступательное движение твердого тела

Поступательным движением твердого тела называется такое движение тела, при котором любая прямая, проведенная в теле движется параллельно самой себе во все время движения.

Теорема о скоростях и ускорениях точек тела при его поступательном движении.

При поступательном движении твердого тела все его точки движутся по одинаковым траекториям, с одинаковыми скоростями и ускорениями.

Доказательство.

Пусть твердое тело движется поступательно. Выберем две произвольно взятые точки и , положение которых определяются радиус-векторами и приложенные к произвольному центру (рис.К.19).

Вектор определяет взаимное положение точек и .

Согласно правилу сложения двух векторов (правило параллелограмма)

Отметим, что вектор является постоянным вектором, так как в процессе движения не меняет ни направление (поскольку совершает поступательное движение) ни модуль (точки и принадлежат абсолютно твердому телу).

Для определения скорости точки продифференцируем уравнение (К.21)

Поскольку является постоянным вектором, то и формула (К.22) принимает вид или

Ввиду произвольности выбора точек и можно утверждать, что все точки твердого тела движутся с одинаковыми скоростями.

Определим теперь ускорение точки , для этого продифференцируем уравнение (К.23), получим

Ввиду произвольности выбора точек и можно утверждать, что все точки твердого тела движутся с одинаковыми ускорениями.

Что и требовалось доказать.

Из доказанной теоремы следует, что поступательное движение твердого тела полностью определяется движением одной произвольно взятой точки.

Траектория точки B получается переносом траектории точки A в пространстве вдоль вектора AB, который не меняет своей величины и направления во времени (AB = const). Следовательно, траектории всех точек твердого тела одинаковы.

Продифференцируем по времени выражение

Продифференцируем по времени скорость и получим выражение a_B = a_A . Следовательно, скорости и ускорения всех точек твердого тела одинаковы.

Для задания поступательного движения твердого тела достаточно задать движение одной из его точек:

Первые два из них – простейшие, а остальные представляют как комбинацию основных движений.

Поступательное криволинейное движение. Угол поворота тела

Поступательным называют движение твердого тела, при котором любая прямая, проведенная в нем, двигается, оставаясь параллельной своему начальному направлению.

Прямолинейное движение является поступательным, но не всякое поступательное будет прямолинейным. При наличии поступательного движения путь тела представляют в виде кривых линий.

Рисунок 1 . Поступательное криволинейное движение кабин колеса обзора

Свойства поступательного движения определяются теоремой: при поступательном движении все точки тела описывают одинаковые траектории и в каждый момент времени обладают одинаковыми по модулю и направлению значениями скорости и ускорения.

Следовательно, поступательное движение твердого тела определено движением любой его точки. Это сводится к задаче кинематики точки.

Если имеется поступательное движение, то общая скорость для всех точек тела υ → называется скоростью поступательного движения, а ускорение a → - ускорением поступательного движения. Изображение векторов υ → и a → принято указывать приложенными в любой точке тела.

Понятие о скорости и ускорении тела имеют смысл только при наличии поступательного движения. В других случаях точки тела характеризуются разными скоростями и ускорениями.

Вращательное движение абсолютно твердого тела вокруг неподвижной оси – это движение всех точек тела, находящихся в плоскостях, перпендикулярных неподвижной прямой, называемой осью вращения, и описывание окружностей, центры которых располагаются на этой оси.

Чтобы определить положение вращающегося тела, необходимо начертить ось вращения, вдоль которой направляется ось A z , полуплоскость – неподвижную, проходящую через тело и движущуюся с ним, как показано на рисунке 2 .

Рисунок 2 . Угол поворота тела

Положение тела в любой момент времени будет характеризоваться соответствующим знаком перед углом φ между полуплоскостями, который получил название угол поворота тела. При его откладывании, начиная от неподвижной плоскости (направление против хода часовой стрелки), угол принимает положительное значение, против плоскости – отрицательное. Измерение угла производится в радианах. Для определения положения тела в любой момент времени следует учитывать зависимость угла φ от t , то есть φ = f ( t ) . Уравнение является законом вращательного движения твердого тела вокруг неподвижной оси.

При наличии такого вращения значения углов поворота радиус-вектора различных точек тела будут аналогичны.

Вращательное движение твердого тела характеризуется угловой скоростью ω и угловым ускорением ε .

Уравнения вращательного движения получают из уравнений поступательного, используя замены перемещения S на угловое перемещение φ , скорость υ на угловую скорость ω , а ускорение a на угловое ε .

Вращательное и поступательное движение. Формулы

Поступательное	Вращательное
Равномерное
s = υ · t	φ = ω · t
υ = c o n s t	ω = c o n s t
a = 0	ε = 0
Равнопеременное
s = υ 0 t ± a t 2 2	φ = ω 0 t ± ε · t 2 2
υ = υ 0 ± a · t	ω = ω 0 ± ε · t
a = c o n s t	ε = c o n s t
Неравномерное
s = f ( t )	φ = f ( t )
υ = d s d t	ω = d φ d t
a = d υ d t = d 2 s d t 2	ε = d ω d t = d 2 φ d t 2

Задачи на вращательное движение

Дана материальная точка, которая движется прямолинейно соответственно уравнению s = t 4 + 2 t 2 + 5 . Вычислить мгновенную скорость и ускорение точки в конце второй секунды после начала движения, среднюю скорость и пройденный за этот промежуток времени путь.

Дано: s = t 4 + 2 t 2 + 5 , t = 2 с .

Найти: s ; υ ; υ ; α .

Решение

s = 2 4 + 2 · 2 2 + 5 = 29 м .

υ = d s d t = 4 t 3 + 4 t = 4 · 2 3 + 4 · 2 = 37 м / с .

υ = ∆ s ∆ t = 29 2 = 14 , 5 м / с .

a = d υ d t = 12 t 2 + 4 = 12 · 2 2 + 4 = 52 м / с 2 .

Ответ: s = 29 м ; υ = 37 м / с ; υ = 14 , 5 м / с ; α = 52 м / с 2

Задано тело, вращающееся вокруг неподвижной оси по уравнению φ = t 4 + 2 t 2 + 5 . Произвести вычисление мгновенной угловой скорости, углового ускорения тела в конце 2 секунды после начала движения, средней угловой скорости и угла поворота за данный промежуток времени.

Дано: φ = t 4 + 2 t 2 + 5 , t = 2 с .

Найти: φ ; ω ; ω ; ε .

Решение

φ = 2 4 + 2 · 2 2 + 5 = 29 р а д .

ω = d φ d t = 4 t 3 + 4 t = 4 · 2 3 + 4 · 2 = 37 р а д / с .

ω = ∆ φ ∆ t = 29 2 = 14 , 5 р а д / с .

ε = d ω d t = 12 2 + 4 = 12 · 2 2 + 4 = 52 р а д / с 2 .

Ответ: φ = 29 р а д ; ω = 37 р а д / с ; ω = 14 , 5 р а д / с ; ε = 52 р а д / с 2 .

Механической системой материальных точек называется совокупность материальных точек, каким-то образом связанных межу собой.
Всякое твердое тело можно считать неизменяемой механической системой материальных точек. Силы взаимодействия точке данной системы называются внутренними силами; силы, с которыми действуют на данную систему другие точки, не входящие в эту систему, - внешними.

Пусть твердое тело массой m движется под действием силы F поступательно с ускорением а (рис. 1) .

Разобьем тело на ряд материальных точек с массами m₁ и применим принцип Даламбера, не забывая при этом, что внутренние силы в уравнение равновесия не входят, так как на основании третьего закона Ньютона их сумма для системы в целом равна нулю.
В каждой материальной точке приложим силу инерции F_i ин = - m_ia и составим уравнение равновесия:

ΣX = 0 ; F – ΣF_i ин = 0 ,

Так как при поступательном движении все точки тела имеют одинаковые ускорения, то а можно вынести за знак суммы, т. е.

Согласно второму закону Ньютона векторы силы F и ускорения а совпадают по направлению, поэтому можно записать:

Это и есть уравнение поступательного движения твердого тела. Очевидно, что это уравнение ничем не отличается от основного уравнения динамики точки, следовательно, все формулы динамики точки применимы для тела, движущегося поступательно.

Уравнение вращательного движения твердого тела

Пусть твердое тело под действием системы сил вращается вокруг неподвижной оси z с угловым ускорением α (рис. 2) .

Разобьем тело на ряд материальных точек с массами m_i и применим, как и в предыдущем случае, принцип Даламбера (Д’Аламбера).
К каждой материальной точке приложены касательная и нормальная силы инерции. Составим уравнение равновесия:

Моменты реакций подшипника и подпятника, а также сил F_τi ин относительно оси z равны нулю, так как линии действия этих сил пересекают ось; сумма моментов внешних сил относительно оси вращения называется вращающим моментом .
Тогда

Выражение Σ(m_ir_i 2 ) называют моментом инерции тела относительно оси и обозначают J :

Момент инерции тела относительно оси есть сумма произведений масс материальных точек, составляющих это тело, на квадрат расстояния от них до этой оси.

В результате получим формулу:

которая называется уравнением вращательного движения твердого тела. В этой формуле J – момент инерции тела относительно оси вращения.

Единица момента инерции - [J] = [mr 2 ] = [m][r 2 ] = кг×м 2 .

Момент инерции играет во вращательном движении такую же роль, какую масса играет в поступательном движении, т. е. момент инерции есть мера инертности вращающегося тела.

В качестве примера определим момент инерции тонкого однородного сплошного диска, радиус которого R , толщина s , масса m , относительно оси, перпендикулярной плоскости диска и проходящей через его центр О (см. рис 3) .

Разобьем диск на элементарные кольца переменного радиуса r , шириной dr и толщиной s . Согласно определению момент инерции такого кольца равен

dJ = dΣ(m_ir 2 ) = r 2 dΣm_i = r 2 dm = r 2 2πr drsρ = 2πsρ r 3 dr ,

где ρ – плотность материала диска.

Просуммировав моменты инерции всех элементарных колец, получим момент инерции всего диска:

J = ∫ 2πsρ r 3 dr = 2πsρ ∫ r 3 dr = 2πsρ r 4 /4 = πsρ r 4 /2 .

Так как масса диска m = πr 2 sρ , то можно записать: J = mR 2 /2 .

Нетрудно понять, что момент инерции однородного сплошного прямоугольного кругового цилиндра радиусом R и массой m любой высоты определяют по такой же формуле. Чтобы убедиться в этом, достаточно мысленно разбить цилиндр плоскостями, параллельными основанию на тонкие диски, и просуммировать моменты инерции всех дисков.

Моменты инерции тел вращения

На основе теоретических выкладок, изложенных выше, мы установили, что момент инерции круглого диска и цилиндрического тела можно определить по формуле

Аналогичные формулы можно вывести для определения моментов инерции других геометрических тел, наиболее часто встречающихся при расчетах и решении задач технической механики.

Моменты инерции для некоторых других однородных тел можно определить по формулам, которые приводятся здесь без вывода.

Шар массой m , радиусом R относительно диаметра:

Тонкий стержень массой m , длиной l относительно оси, проходящей перпендикулярно стержню через его конец:

Тонкая сферическая оболочка массой m , радиусом R относительно диаметра:

Пустотелый вал массой m , наружным радиусом R и радиусом отверстия r относительно оси:

Момент инерции Jz тела относительно какой-либо оси z , параллельной центральной (т. е. проходящей через центр тяжести С тела), равен сумме центрального момента инерции Jc и произведения массы m тела на квадрат расстояния а между этими осями:

Из этой формулы (ее вывод здесь не приводится) следует, что из всех моментов инерции тела относительно параллельных осей наименьшим будет момент инерции относительно центральной оси , т. е. центральный момент инерции.

Иногда момент инерции определяют по формуле: J = mr_и 2 , где r_и – радиус инерции тела :

Физический смысл радиуса инерции следующий: если массу тела сосредоточить в одной точке (такая масса называется приведенной) и поместить ее от оси вращения на расстоянии, равном радиусу инерции, то момент инерции приведенной массы будет равен моменту инерции данного тела относительно той же оси.

Удвоенный радиус инерции тела называется диаметром инерции : D_и = 2r_и .

В практике иногда вместо момента инерции пользуются понятием махового момента GD_и 2 .

Маховым моментом называется произведение силы тяжести G вращающегося тела на квадрат его диаметра инерции.

Единица махового момента - Н×м 2 .

Между маховым моментом и моментом инерции существует простая зависимость:

GD_и 2 = 4g J = 39,24 J .

Кинетическая энергия твердого тела

Кинетическая энергия твердого тела равна сумме кинетических энергий материальных точек, составляющих данное тело:

Определим выражения для кинетической энергии твердого тела для трех случаев движения.

Тело движется поступательно

Учитывая, что при поступательном движении тела все его точки имеют одинаковую траекторию и одинаковые скорости, можно записать:

Следовательно, при поступательном движении твердого тела его кинетическая энергия вычисляется по той же формуле, что и кинетическая энергия материальной точки.

Тело вращается вокруг неподвижной оси

Кинетическая энергия твердого тела, вращающегося вокруг неподвижной оси, равна половине произведения момента инерции тела относительно оси вращения на квадрат его угловой скорости.

Тело движется плоскопараллельно

Как известно из кинематики, сложное плоскопараллельное движение твердого тела в каждый данный момент времени можно считать простейшим вращательным движением вокруг мгновенной оси (метод мгновенных центров скоростей) .
Допустим, что известна скорость v_с центра тяжести тела, тогда мгновенная угловая скорость

где ОС – расстояние центра тяжести С тела от мгновенной оси вращения О .

Момент инерции J_о относительно мгновенной оси вращения определяют по формуле:

где J_с - момент инерции относительно центральной оси или центральный момент инерции.

Кинетическую энергию тела, движущегося плоскопараллельно, определяют следующим образом:

К_пп = J_оω 2 /2 = (J_с + mОС 2 ) ω 2 /2 = (J_сω 2 )/2 + mOC 2 /2×v_с 2 /ОС 2 ,

Кинетическая энергия твердого тела, движущегося плоскопараллельно, равна сумме кинетических энергий в поступательном движении вместе с центром тяжести и вращательном движении вокруг центральной оси, перпендикулярной основной плоскости.

В заключение сформулируем теорему об изменении кинетической энергии системы тел:

Изменение кинетической энергии системы тел при некотором перемещении равно алгебраической сумме работ всех внешних (активных и реактивных) и внутренних сил, действовавших на систему при указанном перемещении:

Кинетическая энергия системы тел равна сумме кинетических энергий каждого тела в отдельности.

Если тело твердое, то сумма работ его внутренних сил равна нулю. При некоторых связях, называемых идеальными, работа реактивных сил тоже будет равна нулю.

Поступательное движение в школьной программе изучает предмет физика. Для понимания, что оно собой представляет, каким законам подчиняется, изучим основную терминологию и рассмотрим понятие на конкретных примерах, которые встречаются в повседневной жизни.

Что такое поступательное движение

Перемещение твердого тела (всех взаимосвязанных его точек) с помощью механического воздействия по заданной траектории и в определенном направлении, в результате которого отрезок из двух любых точек данного тела будет всегда параллелен своему расположению, предшествующему нынешнему, в каждый отрезок времени, называется поступательным движением.

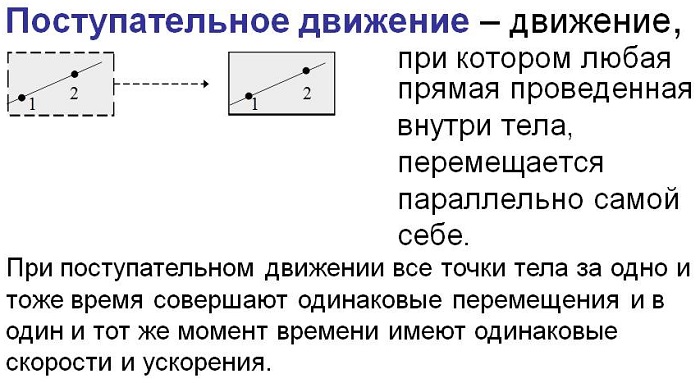
В процессе перемещения характеристика объекта не меняется: по составу, форме и величинам сторон. Причем в любой отрезок времени точки объекта обладают одним и тем же направлением модулей векторов скорости и ускорения, а их величины равны.

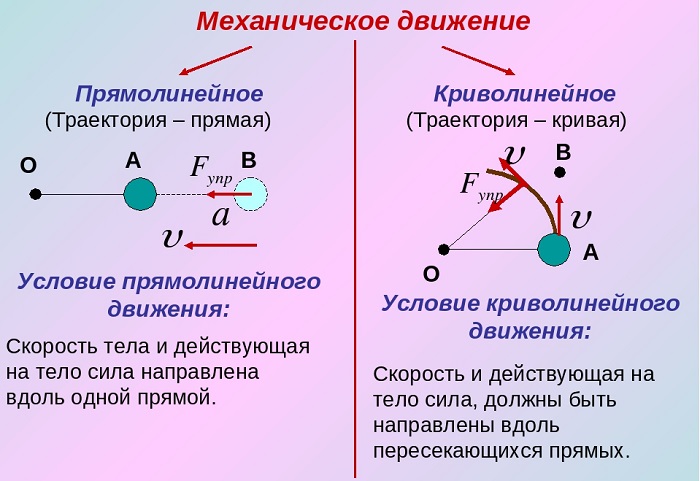
Выделяют прямолинейное поступательное движение и криволинейное.

В качестве примеров поступательного движения в можно привести функционирование по определенной траектории различного оборудования и механизмов.

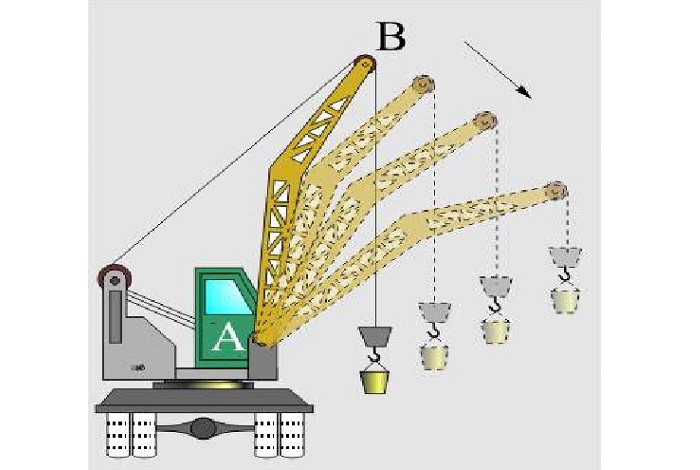
К ним относятся:

перемещение стрелы с грузом строительного подъемного крана относительно его кабины, в которой сидит рабочий;

подъем и спуск лифта в шахте;

педали у велосипеда. При этом каждая его точка, напротив, совершает вращательные движения;

совершение кабиной оборотов на колесе обозрения в парках аттракционов.

Теорема о поступательном движении

Материальные точки объекта (тела), осуществляющего поступательные движения, перемещаются по одному и тому же пути, а скорости и ускорения в каждый промежуток времени совпадают по модулю вектора и направлению.

Доказательство теоремы

Докажем данную теорему. Для этого необходимо провести прямую линию через две любые точки твердого тела, осуществляющего поступательное движение – пусть это будут точки А и В.

Полученный отрезок АВ совершает перемещение по заданному пути: А описывает траекторию АА₁А₂А₃А_n, а В соответственно – В₁В₂В₃В_n.

Отсюда следует, что:

Принимая во внимание, что размеры данного отрезка АВ неизменны (const) при перемещении, а сам он имеет свойство двигаться в пространстве параллельно своему предыдущему местоположению, значит направления точки А и точки В совпадают.

Соотношение радиусов-векторов точек А и В в системе координат относительно ее начала – О (Рис 1),

можно выразить формулой:

где линии пути точки А соответствует функция r_A(t), точки B – r_B(t).

Теорема доказывает, что для определения поступательного движения твердого материального объекта достаточно знать параметры перемещения любой одной его точки. Следовательно, изучая кинематику передвижения точки тела, решается задача определения поступательного движения.

Основной закон динамики поступательного движения

Основной закон динамики поступательного движения трактует II закон Ньютона.

Формулировка закона звучит следующим образом:

Совокупность равнодействующих сил, оказывающих воздействие на материальное тело, способствует возникновению ускорения. То есть, ускорение прямо пропорционально векторному суммарному значению оказываемых на него сил, и обратно пропорционально массе объекта.

Основное уравнение закона приведено ниже:

где m - масса твердого тела;

Причем у равнопеременного движения векторное ускорение

II закон Ньютона работает исключительно в ИСО (инерциальная система отсчета), где объекты двигаются равномерно, прямолинейно или находятся в состоянии покоя.

Читайте также: