Задание положения точки с помощью координат кратко

Обновлено: 02.07.2024

Положение точки задают при помощи системы координат. Чтобы задать положение точки в пространстве, используют три координатные оси: x, y, z. x - лево/право, y - вперед/назад, z - вверх/вниз. Например: точка А находится влево от нуля на 5 единиц, впереди нуля на 3 единицы и выше нуля на 6 единиц. Краткая запись: А (-5; 3; 6).

Как написать хороший ответ? Как написать хороший ответ?

Написать правильный и достоверный ответ;
Отвечать подробно и ясно, чтобы ответ принес наибольшую пользу;
Писать грамотно, поскольку ответы без грамматических, орфографических и пунктуационных ошибок лучше воспринимаются.

Мореплаватель — имя существительное, употребляется в мужском роде. К нему может быть несколько синонимов.
1. Моряк. Старый моряк смотрел вдаль, думая о предстоящем опасном путешествии;
2. Аргонавт. На аргонавте были старые потертые штаны, а его рубашка пропиталась запахом моря и соли;
3. Мореход. Опытный мореход знал, что на этом месте погибло уже много кораблей, ведь под водой скрывались острые скалы;
4. Морской волк. Старый морской волк был рад, ведь ему предстояло отчалить в долгое плавание.

Положение точки в пространстве задается двумя способами:

1) с помощью координат; 2) с помощью радиус-вектора.

Положение точки с помощью координат задается тремя проекциями точки х, у, z на оси декартовой системы координат ОХ, ОУ, ОZ, связанные с телом отсчета (рис. 1.3). Для этого из точки А необходимо опустить перпендикуляры на плоскости УZ (координата х), ХZ (координата у), ХУ (координата z) соответственно. Записывается это так: А (х, у, z). Для конкретного случая, изображенного на рис. 1.3 (х = 6, у = 10, z = 4,5), точка А обозначается A (6; 10; 4,5).

Наоборот, если заданы конкретные значения координат точки в данной системе координат, то для изображения самой точки необходимо отложить значения координат на соответствующие оси (х на ось ОХ и т. д.) и на этих трех взаимно перпендикулярных отрезках построить параллелепипед. Вершина его, противоположная началу координат О и лежащая на диагонали параллелепипеда, и будет искомой точкой А.

Если точка движется в пределах некоторой плоскости, то через выбранные на теле отсчета точки достаточно провести две координатные оси: ОХ и ОУ. Тогда положение точки на плоскости определяют двумя координатами х и у (рис. 1.4).

Задание положения точки А с помощью радиус-вектора осуществляется соединением точки А с началом координат О (рис. 1.4). Направленный отрезок О А = называется радиус-вектором.

Радиус-вектор — это вектор, соединяющий начало отсчета с положением точки в произвольный момент времени.

Точка задана радиус-вектором, если известны его длина (модуль) и направление в пространстве, т. е. значения его проекций rх, ry, rz на оси координат ОХ, ОУ, OZ, либо углы между радиус-вектором и осями координат. Для случая движения на плоскости (рис. 1.4) имеем:

Здесь r = | — модуль радиус-вектора , х и y — его проекции на оси координат, все три величины — скаляры; х и у — координаты точки А.

Последние уравнения демонстрируют связь между координатным и векторным способами задания положения точки.

Вектор г можно также разложить на составляющие по осям X и У, т. е. представить в виде суммы двух векторов (рис. 1.4):

Таким образом, положение точки в пространстве задается либо ее координатами, либо радиус- вектором.

Способы описания движения точки

В соответствии со способами задания координат движение точки можно описать: 1) координатным способом; 2) векторным способом.

При координатном способе описания (или задания) движения изменение координат точки со временем записывается в виде функций всех трех ее координат от времени:

Уравнения (1.1) называют кинематическими уравнениями движения точки, записанными в координатной форме. Зная кинематические уравнения движения и начальные условия (т. е. положение точки в начальный момент времени), можно определить положение точки в любой момент времени.

При векторном способе описания движения точки изменение ее положения со временем задается зависимостью радиус-вектора от времени:

Уравнение (1.2) представляет собой уравнение движения точки, записанное в векторной форме. Если оно известно, то для любого момента времени можно рассчитать радиус-вектор точки, т. е. определить ее положение (как и в случае координатного способа). Таким образом, задание трех скалярных уравнений (1.1) равносильно заданию одного векторного уравнения (1.2).

Для каждого случая движения вид уравнений (1.1) или (1.2) будет вполне определенным. Если траекторией движения точки является прямая линия, движение называетсяпрямолинейным, а если кривая — криволинейным.

Библиотека образовательных материалов для студентов, учителей, учеников и их родителей.

Наш сайт не претендует на авторство размещенных материалов. Мы только конвертируем в удобный формат материалы из сети Интернет, которые находятся в открытом доступе и присланные нашими посетителями.

Если вы являетесь обладателем авторского права на любой размещенный у нас материал и намерены удалить его или получить ссылки на место коммерческого размещения материалов, обратитесь для согласования к администратору сайта.

Разрешается копировать материалы с обязательной гипертекстовой ссылкой на сайт, будьте благодарными мы затратили много усилий чтобы привести информацию в удобный вид.

Положение точки в пространстве можно задать двумя способами: координатным и векторным.

При задании движения координатным способом с телом отсчета связывают какую-либо систему координат, например, декартовую. Движение точки М будет задано в том случае, если ее координаты будут известны, как функции времени:

Эти зависимости называются уравнениями движения точки в декартовых координатах. Они выражают текущие координаты движущейся точки в виде функций времени. Если точка движется, оставаясь все время в одной плоскости, можно ограничиться двумя уравнениями движения: x = x(t), y = y(t).

Векторный способ задания положения точки .

Допустим, М – движущаяся точка относительно тела отсчета А. В теле А в качестве точки отсчета выберем произвольную точку О и построим вектор Этот вектор называется радиус-вектором точки М.

Радиус-вектор – это вектор, соединяющий начало отсчета с положением точки в любой момент времени.

Когда точка М движется, радиус-вектор непрерывно изменяется во времени, поэтому существует некоторая вектор-функция времени Зная эту функцию, для каждого времени t можно построить вектор и тем самым найти положение движущейся точки в данный момент. Функция называется векторным законом (векторным уравнением) движения точки М.

Точка задается радиус-вектором, если известны его длина (модуль) и направление в пространстве, другими словами – значения его проекций r_x, r_y, r_z на оси координат OX, OY и OZ, или углы между радиус-вектором и осями координат. При рассмотрении движения на плоскости:

Здесь за мы принимаем модуль радиус-вектора , а r_x и r_y являются его проекциями на оси координат, все три величины скалярны, x и y – координаты точки А.

Из этих уравнений видно, что между координатным и векторным способами задания положения точки существует связь.

Движение. Виды движений. Описание движения. Система отсчета.

Механическим движением тела (точки) называется изменение его положения в пространстве относительно других тел с течением времени.

Виды движений:

А) Равномерное прямолинейное движение материальной точки.

Б) Равноускоренное прямолинейное движение материальной точки.

В) Движение тела по дуге окружности с постоянной по модулю скоростью.

Г) Гармоническое колебательное движение. Важным случаем механического движения являются колебания, при которых параметры движения точки (координаты, скорость, ускорение) повторяются через определенные промежутки времени.

Описания движения .

1. Векторный способ описания движения

ОПРЕДЕЛЕНИЕ: Векторный способ описания движения – это описание изменения радиус-вектора материальной точки в пространстве с течением времени.

Рассмотрим движение точки М в некоторой системе отсчета Oxyz (рис.1). Зададим радиус-вектор точки r — вектор, соединяющий начало координат с этой точкой.

При движении точки M вектор r будет с течением времени изменяться, т.е. будет каким-то образом зависеть от времени. Эта зависимость r = r ( t ) представляет собой закон движения в векторном виде.

В процессе движения конец радиус-вектора будет описывать траекторию, а его изменение – перемещение s точки.

2. Координатный способ описания движения

ОПРЕДЕЛЕНИЕ: Координатный способ описания движения – описание изменения во времени координат точки в выбранной системе отсчета.

При координатном способе положение точки в пространстве задается тремя координатами (рис.2). Выбор системы координат зависит от конкретной задачи. Можно работать в декартовой (прямоугольной) системе, иногда удобнее бывает сферическая или цилиндрическая системы координат.

В декартовой системе координат положение точки определяется тройкой чисел ( x , y , z ) — ее декартовыми координатами.

Чтобы задать закон движения точки, необходимо знать значения ее координат в каждый момент времени. Закон движения в координатном виде в общем случае представляет собой систему трех уравнений: x = x ( t ), y = y ( t ), z = z ( t )

Между векторным и координатным способом описания движения существует непосредственная связь, а именно: числовые значения проекций радиус-вектора движущейся точки на координатные оси системы с тем же началом отсчета равны координатам точки: r_x = x , r_y = y , r_z = z .

3. Естественный способ описания движения

ОПРЕДЕЛЕНИЕ: Естественный способ описания движения – описание движения вдоль траектории. Этим способом пользуются, когда траектория точки заранее известна.

Пусть точка М движется вдоль траектории АВ в системе отсчета Oxyz (рис.3). Выберем на траектории какую-нибудь неподвижную точку О 1 , которую будем считать началом отсчета, и определим положительное и отрицательное направления. Тогда положение точки M будет определяться расстоянием S от точки О 1 . При движении точка М переместится в точку М 1 , соответственно изменится ее расстояние от точки О 1 . Таким образом, расстояние S зависит от времени, а характер этой зависимости позволит определить положение точки М на траектории в любой момент времени. Закон движения в этом случае имеет вид: s = s ( t ) .

Пример 1

Пример 2

Под системой отсчета понимают тело отсчета, которое условно считается неподвижным, систему координат, связанную с телом отсчета, и часы, также связанные с телом отсчета. В кинематике система отсчета выбирается в соответствии с конкретными условиями задачи описания движения тела.

Чтобы говорить о положении каких-либо тел, необходимо определиться с тем, как обозначать это положение. Какими величинами мы можем характеризовать положение того или иного тела, сколько параметров для этого нужно? На этом уроке мы и рассмотрим данные вопросы.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.

Получите невероятные возможности

Конспект урока "Положение и движение точки в пространстве"

Мы продолжаем тему классической механики Ньютона. Механика делится на два основных раздела: кинематика и динамика. Мы начнём с изучения кинематики.

Кинематика изучает движение тел, способы описания этого движения, а также, его характеристики.

Описать движение человека или полет бабочки математически — это крайне сложная задача. Но есть задачи и проще: например, описать движение материальной точки. Добавим теперь, что эта точка двигается равномерно и прямолинейно. Тогда, описать её движение не так уж сложно. Именно с таких идеализированных моделей и следует начать изучение кинематики. Ведь если мы сможем описать движение каждой точки тела, то мы также сможем описать движение самого тела.

В первую очередь, нужно создать систему отсчёта. Система отсчёта состоит из тела отсчёта, системы координат и счётчика времени.

Тело отсчёта — это физическое тело, относительно которого задаётся положение данного тела или точки.

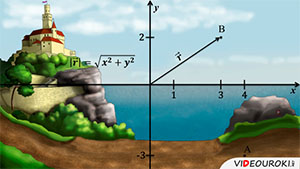
Понять это довольно просто. На рисунке изображено дерево.

На каком расстоянии находится это дерево? На каком расстоянии от чего? — спросите вы. Конечно, нам нужно выбрать точку отсчета. Это может быть белый треугольник на камне, а может быть флажок на за́мке. В зависимости от этого выбора, ответ на вопрос будет различным. Необходимо выбрать какую-то точку за точку отсчёта, то есть за ноль. Скажем, мы можем обозначить за ноль центр картинки.

Далее, мы используем декартовы координаты, чтобы описать положения тел. Выбираем единичный отрезок и, исходя из этого определяем положения тел. Это положение задаётся с помощью координат. Например, точка А имеет координаты четыре и минус три, а точка Б — три и два. Также, можно задать положение тела с помощью радиус-вектора — это вектор, который соединяет точку и начало координат.

Радиус-вектор обозначается латинской буквой r и, как и любой другой вектор, имеет длину и направление. Длиной радиус-вектора будет является геометрическая сумма координат точки. Иными словами, мы вычисляем длину радиус-вектора, используя теорему Пифагора. То есть, длина радиус-вектора, описывающего положение точки B будет равна .

Модуль и направление любого вектора находят с помощью проекций этого вектора на оси координат.

Что же такое проекция? Давайте рассмотрим вектор с начальной точкой А и конечной точкой B, находящийся в системе координат на плоскости.

Из точек А и B опустим перпендикуляры на ось икс. Длина отрезка А₁ B₁ — это и есть проекция вектора цэ на ось x. Точно таким же способом находится проекция вектора на ось y. Как видно из построения: . Аналогично можно найти проекцию на ось y: ..

Проекция вектора на ось — это алгебраическая величина. Её знак можно определить так: если, двигаясь от начальной точки проекции до конечной точки проекции, надо идти в положительном направлении, то проекция положительная, а в противном случае — она отрицательная.

Иначе это можно объяснить так: если вектор составляет острый угол с направлением оси, на которую мы собираемся сделать проекцию, то проекция будет положительной, а если угол между вектором и направлением оси — тупой, то проекция будет отрицательной.

Нетрудно догадаться, что если вектор перпендикулярен оси, то его проекция на эту ось будет равна нулю.

Аналогично, если вектор параллелен оси, то его проекция на эту ось будет равна модулю вектора.

Рассмотрим теперь, как задать положение точки в пространстве, а не на плоскости. Как вы знаете, у есть три пространственных измерения, поэтому, чтобы задать положение точки в пространстве нам нужно три координаты. Сначала мы точно также, как и ранее, находим точку на плоскости, а потом от этой точки откладываем числовое значение координаты z параллельно оси Z.

Положение такой точки точно также можно задать с помощью радиус-вектора. Его модуль также будет находиться с помощью геометрической суммы координат точки.

Примеры решения задач.

Задача 1. В системе координат отметьте точку N (1;3;7), постройте соответствующий радиус-вектор и найдите его длину.

Задача 2. В системе координат отметьте точку N (1;3;7), постройте соответствующий радиус-вектор и найдите его длину.

Задача 3. Постройте проекции вектора на оси x и y и найдите их числовые значения, если , а угол между и осью x составляет 30.

Читайте также: