Взаимное расположение прямой и плоскости кратко
Обновлено: 02.07.2024
Примером пространственной фигуры может служить геометрическое тело – часть пространства, занимаемое предметом. Геометрическое тело отделяется от окружающего пространства поверхностью.
Две геометрические фигуры называются равными, если их можно совместить так, чтобы они совпали всеми своими частями.
Предполагается, что при перемещении в пространстве геометрические фигуры не изменяются. Пространственные фигуры изображаются на чертеже в виде рисунков, которые выполняются по определённым правилам, основанным на геометрических свойствах фигур.
– через любые три точки пространства, которые не лежат на одной прямой, можно провести плоскость, и к тому же только одну ;
– если две плоскости имеют общую точку, то они пересекаются по прямой, которая проходит через эту точку ;
– через прямую и точку, лежащую вне этой прямой, можно провести плоскость, и к тому же только одну ;
Множество плоскостей, которые проходят через некоторую прямую, называют пучком плоскостей, а прямую, через которую они проходят, – осью пучка. Плоскость на рисунку изображается в виде параллелограмма и обозначается одной буквой, например Р .

– две прямые лежат в одной плоскости, при этом они могут или иметь общую точку, то есть пересекаются, или не иметь общих точек, тогда их называют параллельными ;
– две прямые не лежат в одной плоскости и, следовательно, не имеют общих точек, тогда их называют скрещивающимися.
Условились считать, что угол между двумя скрещивающимися прямыми равняется углу, образованному двумя лучами, выходящими из одной точки и параллельными этим скрещивающимся прямым.

На рисунку прямые АВ и СD – скрещивающиеся, а лучи ОМ ∥ АВ и ОN ∥ СD ; угол между мимолетными прямыми считают таким, который равняется углу МОN .
Расстоянием между двумя параллельными прямыми считают длину заключенного между ними отрезка прямой, перпендикулярной к каждой из параллельных прямых и пересекающей их.
Расстояние между скрещивающимися прямыми измеряется длиной отрезка прямой, перпендикулярной к каждой из скрещивающихся прямых и пересекающей каждую из них в точках, являющихся концами этого отрезка. Расстояние между двумя скрещивающимися прямыми есть наименьшее расстояние между точками, лежащими на этих прямых.

АВ , лежащая в плоскости Р , и СD , пересекающая эту плоскость. Прямая МN перпендикулярна как к АВ , так и к СD . Тогда длина отрезка МN есть расстояние между скрещивающимися прямыми АВ и СD .
– прямая и плоскость имеют одну общую точку, то есть прямая пересекает плоскость ; точку их пересечения называют следом прямой на данной плоскости;
Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, которая лежит на этой плоскости.
Прямая, которая пересекает плоскость, но не перпендикулярная к ней, называется наклонной к этой плоскости.
Если прямая перпендикулярна до двух прямых, которые пересекаются и лежат в некоторой плоскости, то она перпендикулярна и к любой прямой, которая лежит в данной плоскости, то есть прямая перпендикулярна к плоскости.
Прямоугольной проекцией точки на плоскость называется след перпендикуляра, проведенного через эту точку к данной плоскости. След перпендикуляра на плоскости называется основанием перпендикуляра, а след наклонной – основанием наклонной.
Прямоугольной проекцией наклонной на плоскость называется отрезок прямой, соединяющий основание наклонной и основание перпендикуляра, опущенного из конца наклонной на эту плоскость.
На рисунку АВ , АС и АD – наклонные к плоскости Р , а АО – перпендикуляр к этой плоскости. Тогда, если проекция ОВ = ОС , то и наклонные АВ = АС ; если ОD , то и соответственно наклонные АD .

Если из одной и той же точки, лежащей вне плоскости, провести к этой плоскости перпендикуляр и наклонный, то :
Прямая, проведенная на плоскости перпендикулярно к наклонной, перпендикулярна к проекции этой наклонной на данную плоскость.
Прямая, проведенная на плоскости перпендикулярно к проекции наклонной на эту плоскость, перпендикулярна к самой наклонной.
На рисунку АВ – наклонная, а АС – перпендикуляр к плоскости Р ; если MN ⊥ AB , то и MN ⊥ DC и, наоборот, если MN ⊥ CB , то и MN ⊥ AB .

Углом между прямой и плоскостью называют острый угол между этой прямой и ее проекцией на данную плоскость.
На рисунку АВ – наклонная, а СD – её проекция на плоскость Р . Тогда угол между АВ и плоскостью Р равен ∠ АВС .

Угол между прямой и плоскостью наименьший из всех углов, образованных этой прямой с любой прямой, которая лежит в данной плоскости.
Из некоторой точки пространства проведены к данной плоскости две наклонные, каждая из которых равна а , угол между ними равен 60 ° , а угол между их проекциями на данную плоскость – прямой.

∆ АВС – равнобедренный с углом 60 ° при вершине, т. е. равносторонний, поэтому расстояние между основаниями наклонных
ВС = а .
∆ ВОС – равнобедренный прямоугольный (так как проекции ОВ и ОС равных наклонных АВ и АС равны ), гипотенуза которого
ВС = а ,
тогда проекция


∠ АСО = ∠ АВО = 45 ° , так как прямоугольные ∆ АВО и ∆ АОС равны между собою и одновременно являются равнобедренными треугольниками :


Если плоскость Р и прямая АВ , которая не лежит в плоскости Р , перпендикулярные к одной и той же прямой СD , то они параллельны.
Если прямая АВ параллельна к прямой СD , которая лежит в плоскости Р , то она параллельная к плоскости Р .

Если две плоскости Р и Q , что проходят соответственно через параллельные прямые АВ и СD , пересекаются, то линия их пересечения МN параллельна до обоих данных прямых АВ и СD.

Если плоскость проходит через прямую, параллельную к другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна к данной прямой.
Если прямая параллельна к каждой из двух плоскостей, которые пересекаются, то она параллельна к линии их пересечения.
Если одна из двух параллельных прямых параллельная к некоторой плоскости, то и вторая прямая параллельная к той же плоскости или лежит в ней.
Через каждую из двух скрещивающихся прямых проходит плоскость, и к тому же только одна, параллельная к другой прямой.
Правильный треугольник спроектирован на плоскость Р . Вершины треугольника отстоят от этой плоскости на 10, 15 и 17 дм. Найти расстояние от центра треугольника до плоскости Р.

Расстояние от центра правильного треугольника до некоторой плоскости равно среднему арифметическому расстояний от его вершин до этой плоскости.

– если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости, то такие две плоскости параллельные.
Если пересекающиеся прямые АВ м ВС , лежат в плоскости Р , а прями А 1 В 1 и В 1 С 1 – лежат в плоскости Q и
АВ ∥ А 1 В 1 , а
СВ ∥ C 1 B 1 , то
Р ∥ Q .

Если плоскости Р и Q параллельны и плоскость М их пересекает, то прямые пересечения этих плоскостей АВ и СD параллельны.

– если прямая перпендикулярна одной из двух параллельных плоскостей, то она перпендикулярна и к другой плоскости ;
Отрезки двух прямых, заключённые между двумя параллельными плоскостями, равны 51 см и 53 см, а их проекции на одну из этих плоскостей относятся, как 6 : 7 . Определить длину этих проекций и расстояние между данными плоскостями.

Требуется определить ВС , В 1 С 1 и АС. Обозначим
ВС = 6х, В 1 С 1 = 7х
и, учитывая, что АС = А 1 С 1 и з треугольников АВС и А 1 В 1 С 1 получим
Определив ВС и, зная АВ , находим из треугольника АВС по теореме Пифагора расстояние между плоскостями :

Часть плоскости, лежащая по одну сторону какой-либо прямой, принадлежащей этой плоскости, называется полуплоскостью.
Двугранным углом называется геометрическая фигура, образованная двумя полуплоскостями Р и Q , что выходят из одной прямой АВ .

Двугранный угол обозначают или двумя буквами, поставленными у ребра, например АВ , или четырьмя буквами РАВQ , из которых две средние означают ребро, а крайние – грани.
Линейным углом двугранного угла называется угол, образованный двумя перпендикулярами, восстановленными к ребру из произвольной его точки и лежащими на гранях угла.

ОN лежит в плоскости Р , а ОМ – в плоскости Q , причём ОN ⊥ АВ и ОМ ⊥ АВ , тогда угол МОN называется линейным углом двугранного угла РАВQ .
Если совместить по одной грани два неравных двугранных угла, то больше считается тот из них, между гранями которого находится другая грань второго двугранного угла. На рисунку двугранный угол РАВQ больше за двугранного угла РАВМ .

Если два двугранных угла не равны, то большему двугранному углу соответствует и больший линейный угол.
Двугранные углы называются смежными, если у них одна грань общая, а две другие составляют одну плоскость.
Двугранный угол измеряется его линейным углом, т. е. за единицу измерения двугранных углов принимается такой двугранный угол, линейный угол которого содержит единицу измерения линейных углов. Так, двугранный угол в 1 ° есть угол, линейный угол которого содержит 1 ° , двугранный угол в 1 радиан есть угол, линейный угол которого содержит 1 радиан.
Если плоскость Р проходит через перпендикуляр АВ к плоскости Q , то плоскости Р и Q взаимно перпендикулярны.

Если две плоскости взаимно перпендикулярны, то любая прямая, что лежите в одной из них и перпендикулярная к линии их пересечения, перпендикулярная другой плоскости.
Если две плоскости взаимно перпендикулярные и из какой-либо точки одной из них опущен перпендикуляр на другую, то этот перпендикуляр лежит в первой плоскости.
Плоскость, перпендикулярная двум пересекающимся плоскостям, перпендикулярна ребру, образованного ими двугранного угла.
Катеты прямоугольного треугольника равны а і b . Определить расстояние от вершины прямого угла до плоскости, которая проходит через гипотенузу и составляет угол в 30 ° с плоскостью треугольника.

По теореме о трёх перпендикулярах ОD как проекция наклонной СD на плоскость Р перпендикулярна АВ . Тогда угол
СDО = 30 °
– линейный угол двугранного угла, образованного плоскостью ∆ АВС и плоскостью Р . Из ∆ АВС находим
Все возможные случаи взаимного расположения прямой и плоскости в пространстве представлены в следующей таблице.
Прямая лежит на плоскости, если все точки прямой принадлежат плоскости.
Замечание . Для того, чтобы прямая лежала на плоскости, необходимо и достаточно, чтобы две любые точки этой прямой принадлежали этой плоскости.
Прямая пересекает плоскость, если прямая и плоскость имеют единственную общую точку.
Прямая параллельна плоскости, если прямая и плоскость не имеют общих точек. (они не пересекаются)


Прямая лежит на плоскости, если все точки прямой принадлежат плоскости.
Замечание . Для того, чтобы прямая лежала на плоскости, необходимо и достаточно, чтобы две любые точки этой прямой принадлежали этой плоскости.


Прямая пересекает плоскость, если прямая и плоскость имеют единственную общую точку.


Прямая параллельна плоскости, если прямая и плоскость не имеют общих точек. (они не пересекаются)
Утверждение 1 . Предположим, что прямая a и плоскость α параллельны, а плоскость β проходит через прямую a . Тогда возможны два случая:
- Плоскость β параллельна плоскости αПлоскость β параллельна плоскости α (рис.1);
- Плоскость β пересекает плоскость α . В этом случае прямая b , которая является линией пересечения плоскостей α и β , будет параллельна прямой aпрямая b , которая является линией пересечения плоскостей α и β , будет параллельна прямой a (рис.2).
 |
| Рис.1 |
 |
| Рис.2 |
Доказательство . Рассмотрим случай 2 и предположим противное. Предположим, что прямые a и b пересекаются в некоторой точке P (рис.3) .



Но тогда точка P оказывается точкой пересечения прямой a и плоскости α , и мы получаем противоречие с тем, что прямая a и плоскость α параллельны. Полученное противоречие и завершает доказательство утверждения 1.
Утверждение 2 (признак параллельности прямой и плоскости) . Если прямая a , не лежащая в плоскости α , параллельна некоторой прямой b , лежащей в плоскости α , то прямая a и плоскость α параллельны.
Доказательство. Докажем признак параллельности прямой и плоскости "от противного". Предположим, что прямая a пересекает плоскость α в некоторой точке P . Проведем плоскость β через параллельные прямые a и b Проведем плоскость β через параллельные прямые a и b (рис. 4).



Точка P лежит на прямой a и принадлежит плоскости β. Но по предположению точка P принадлежит и плоскости α , следовательно точка P лежит на прямой b , по которой пересекаются плоскости α и β . Однако прямые a и b параллельны по условию и не могут иметь общих точек.
Полученное противоречие завершает доказательство признака параллельности прямой и плоскости.
Плоскости окружают нас со всех сторон. Примеры плоских поверхностей: стол, стены, пол и потолок, школьная доска, скамейка, экран, грани карандаша. Плоскость — одно из важнейших понятий геометрии и стереометрии, математики давно пытаются дать ее точное определение.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Плоскость — это такая поверхность, в которой целиком лежит всякая прямая, соединяющая две любые точки этой поверхности.
Обозначение плоскости
Плоскость обозначают строчными буквами греческого алфавита: α (альфа), β (бета), γ (гамма) и т.д.
Как выяснить взаимное расположение прямой и плоскости
Есть три варианта взаимного расположения прямой и плоскости в пространстве:
- Прямая и плоскость пересекаются.
- Прямая принадлежит плоскости (лежит в ней).
- Прямая и плоскость параллельны.
Рассмотрим каждый вариант подробней.
Прямая пересекает плоскость
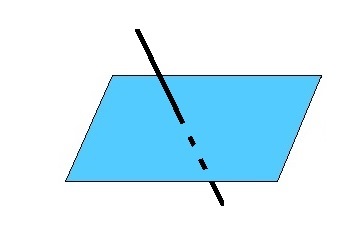
Прямая и плоскость пересекаются, если они имеют только одну общую точку.
Прямая принадлежит плоскости
Прямая принадлежит плоскости (лежит в плоскости), если все точки прямой лежат в плоскости. При этом достаточно, чтобы две любые точки данной прямой лежали в данной плоскости.
Все точки прямой лежат в плоскости, если хотя бы две точки данной прямой лежат в данной плоскости.
Прямая параллельна плоскости
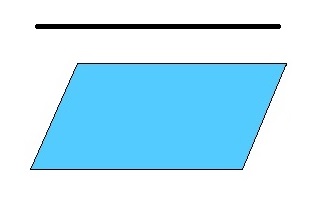
Прямая, не лежащая в плоскости, пересекается с плоскостью или параллельна ей. Прямая и плоскость параллельны, если они не имеют общих точек. Отсутствие общих точек — признак параллельности прямой и плоскости.
Прямая параллельна плоскости, если она параллельна одной из прямых, лежащих в плоскости.
Различные способы задания прямой на плоскости
Положение прямой определяют:
-
Две заданные точки. Через две точки можно провести только одну прямую. Поэтому координаты точек в прямоугольной системе координат задают отрезок или прямую.


Как найти угол между прямой и плоскостью
Чтобы найти угол между прямой и плоскостью, нужно знать, каков угол между прямой и ее проекцией на эту плоскость.
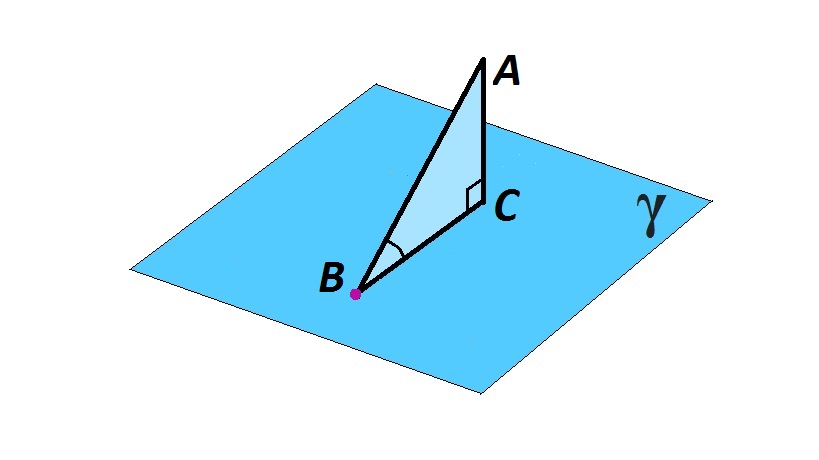
На изображении прямая АВ пересекает плоскость γ, и является наклонной к этой плоскости. Проведем перпендикуляр АС. ВС — проекция наклонной АВ. Угол между АВ и γ будет равен ∠АВС прямоугольного ΔАСВ.
Как Волга неизбежно впадает в Каспийское море, так и плоскость в пространстве неминуемо встречается с прямой линией. И вот, после рассмотрения уравнения плоскости, уравнений пространственных прямых с типовыми задачами, настал долгожданный момент встретить бурными аплодисментами ещё целую группу примеров на плоскость и прямую в пространстве. Со многими приёмами решений мы уже знакомы из предыдущих уроков, поэтому особых трудностей возникнуть не должно. И сейчас я расскажу вам сказочку: Жили-были плоскость и прямая…. …так, стоп, надо умерять свои писательские потребности, а то сейчас уже пойдут откровенные гонки =) Давно думаю о своём блоге, да всё времени не хватает…. Высшей математики целый океан, и я приглашаю всех читателей зачистить бананы на очередном острове:
Взаимное расположение прямой и плоскости
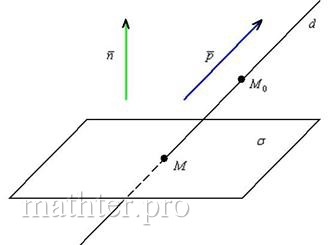
Рассмотрим плоскость и прямую , заданную точкой и направляющим вектором .
Существует три варианта взаимного расположения прямой и плоскости:
1) прямая пересекает плоскость в некоторой точке ;
2) прямая параллельна плоскости: ;
3) прямая лежит в плоскости: . Да, так вот нагло взяла, и лежит.
Как выяснить взаимное расположение прямой и плоскости?
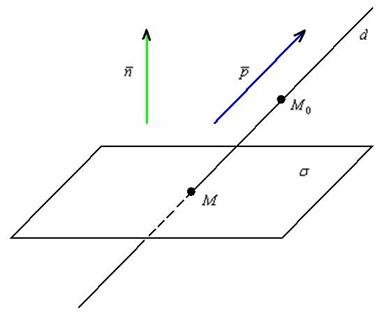
Изучим аналитические условия, которые позволят нам ответить на данный вопрос. Выполним схематический чертёж, на котором прямая пересекает плоскость:
Прямая пересекает плоскость тогда и только тогда, когда её направляющий вектор не ортогонален вектору нормали плоскости.
Из утверждения следует, что скалярное произведение вектора нормали и направляющего вектора будет отлично от нуля: .
В координатах условие запишется следующим образом:
Если же данные векторы ортогональны, то есть если их скалярное произведение равно нулю: , то прямая либо параллельна плоскости, либо лежит в ней:
Разграничим данные случаи.
Если прямая параллельна плоскости, то точка (а значит, и ЛЮБАЯ точка данной прямой) не удовлетворяет уравнению плоскости: .
Таким образом, условие параллельности прямой и плоскости записывается следующей системой:
Если прямая лежит в плоскости, то точка (а, значит, и ЛЮБАЯ точка данной прямой) удовлетворяет уравнению плоскости: .
Аналитические условия данного случая запишутся похожей системой:
Разборки с взаимным расположением прямой и плоскости достаточно примитивны – всего в два шага. Кроме того, на практике можно обойтись даже без значка системы. Исследование взаимного расположения прямых в пространстве, которое проводилось на уроке Задачи с прямой в пространстве, намного трудозатратнее. А тут всё проще:
Выяснить взаимное расположение прямой, заданной точкой и направляющим вектором , и плоскости .
Решение: Вытащим вектор нормали плоскости: .
Вычислим скалярное произведение вектора нормали плоскости и направляющего вектора прямой: , значит, прямая либо параллельна плоскости, либо лежит в ней.
Подставим координаты точки в уравнение плоскости:
Получено верное равенство, следовательно, точка лежит в данной плоскости. Разумеется, и любая точка прямой тоже будет принадлежать плоскости.
Ответ: прямая лежит в плоскости
Выяснить взаимное расположение плоскости и прямой .
Это пример для самостоятельного решения. Примерный образец оформления и ответ в конце урока.
После небольшой разминки мускулатуры начинаем накидывать блины на штангу:
Основные задачи на прямую и плоскость
Данная задача прям таки вертится в умах человечества, и встречается в практических задачах чаще всего. Когда я приступил к разработке пространственной геометрии, то, начиная с урока Уравнение плоскости, мне даже было немного неловко, что посетители сайта обманывались в своих ожиданиях. Многие задачи уже были, а вот этой ещё нет….
Рассмотрим прямую , которая пересекает плоскость . Требуется найти точку, в которой прямая пересекает плоскость: . Хотел разобрать задачу в общем виде, но передумал… лучше традиционный практический пример:
Дана прямая и плоскость . Требуется:
а) доказать, что прямая пересекает плоскость;
б) найти точку пересечения прямой и плоскости;
г) найти проекцию прямой на плоскость ;
д) найти угол между прямой и плоскостью .
НеслАбо. А ведь всё началось с единственной точки пересечения =)
Решение: Сначала закрепим задачу о взаимном расположении прямой и плоскости:
а) Из уравнений прямой находим принадлежащую ей точку и направляющий вектор:
Вектор нормали плоскости, как всегда, сдаётся без боя:
Вычислим скалярное произведение:
, значит, прямая пересекает плоскость, что и требовалось доказать.
Как найти точку пересечения прямой и плоскости?
Точка принадлежит данной прямой, поэтому её координаты при некотором значении параметра удовлетворяют параметрическим уравнениям:
, или одной строчкой: .
С другой стороны, точка принадлежит и плоскости , следовательно, координаты точки должны удовлетворять уравнению плоскости , то есть должно выполняться равенство:
– ну, или попросту параметрические координаты точки нужно подставить в уравнение плоскости.
– полученное значение параметра подставляем в параметрические выражения координат нашей точки:
Интересно, что в данном пункте всё обошлось даже без векторов.
в) Найдём уравнение плоскости , которая перпендикулярна плоскости и проходит через прямую . Задача весьма напоминает Пример № 12 урока Уравнение плоскости, в котором мы рассмотрели построение перпендикулярной плоскости, проходящей через две точки.
Выполним схематический чертёж:
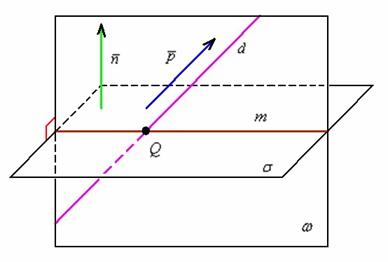
Уравнение плоскости можно составить по любой точке, которая принадлежит прямой , направляющему вектору прямой и вектору нормали плоскости .
Как найти уравнения проекции прямой на плоскость?
г) По умолчанию под проекцией понимается, как правило, ортогональная проекция. Что это такое и что это значит?
Физкульт-пятиминутка. Пожалуйста, найдите дома швабру или метлу и поместите её между своих ног. Подбородок плотно прижат к груди. Теперь строго перпендикулярно смотрим вниз на швабру. при этом получается такое умное лицо…. Скрытая от вас часть пола – это и есть проекция швабры на плоскость. Да… …а я как погляжу, вы без комплексов =)
Другое дело, что часто требуется представить уравнения прямой в канонической форме. Это стандартная задача, рассмотренная в Примерах № 9, 10 урока Уравнения прямой в пространстве.
Точка , принадлежащая проекции, уже известна, осталось найти её направляющий вектор:
Таким образом, канонические уравнения проекции:
Обратите внимание, что на практике для решения данной задачи, в общем-то, не надо находить именно точку пересечения (лишняя работа). Нас устроит любая точка, принадлежащая проекции. Красавица подбирается из системы (см. Примеры № 9, 10 урока Уравнения прямой в пространстве).
– находим точку пересечения прямой и плоскости: (вот в этом способе уже обязательно находим);
– из произвольной точки (не совпадающей с точкой ) опускаем перпендикуляр на плоскость (см. следующие параграфы);
– основание перпендикуляра находим как пересечение прямой и плоскости ;
– составляем канонические уравнения проекции по двум точкам: .
Как найти угол между прямой и плоскостью?
д) Логическое продолжение темы.
Если прямая не перпендикулярна плоскости , то углом между прямой и плоскостью называется острый угол между прямой и её проекцией на плоскость . Если прямая перпендикулярна плоскости, то угол между ними равен 90 градусов.
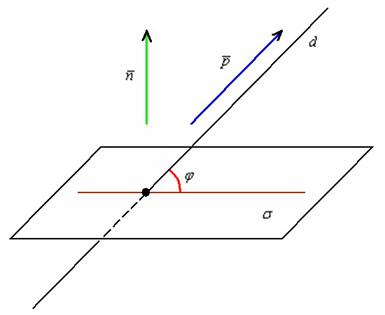
Продолжим эксплуатацию геометрического инвентаря:
Справедлива следующая формула синуса угла между прямой и плоскостью:
(вывод формулы можно посмотреть, например, в учебнике Атанасяна-Базылева).
Таким образом, для нахождения данного угла достаточно знать лишь нормальный вектор плоскости и направляющий вектор прямой.
Вычислим длины векторов:
На иррациональность в знаменателе забиваем, поскольку нам нужен сам угол:
Выложим в ряд головы очередного Змея-Горыныча:
Ответ:
а) , значит, прямая пересекает плоскость;
б) ;
в) ;
г) ;
д)
Переходим к рассмотрению частного случая – когда:
Прямая перпендикулярна плоскости
В данном параграфе мы разберём ещё несколько распространённых задач. Чувствую, вы немного заскучали, поэтому пора предложить живительные примеры для самостоятельного решения. А потом ещё десяток =)
Дана плоскость и точка . Требуется:
а) составить канонические уравнения прямой , проходящей через точку , перпендикулярно данной плоскости;
б) найти точку пересечения перпендикулярной прямой и плоскости;
в) найти точку , симметричную точке относительно плоскости .
в) Рассмотрим отрезок . Если точка симметрична точке относительно плоскости, то, очевидно . Саму длину перпендикуляра мы рассчитывали в Примере № 9 на уроке Уравнение плоскости, но сейчас речь не о длине. Точка делит отрезок пополам. По условию нам дан один из концов отрезка , а в предыдущем пункте найдена середина . Таким образом, по формулам деления отрезка пополам, нетрудно найти координаты нужной точки .
Полное решение и ответ в конце урока. Постарайтесь не заглядывать в образец, сложного-то здесь ничего нет.
Вопрос очевидный, но на всякий случай коснёмся обратной задачи: как составить уравнение плоскости, которая проходит через данную точку перпендикулярно данной прямой? Берём направляющий вектор прямой – он же является вектором нормали плоскости.
Поставлю и другую заплату, вроде в явном виде нигде не упоминал: можно ли составить уравнение плоскости, проходящей через прямую и точку, не принадлежащую прямой? Да, конечно, причём плоскость будет определена однозначно. Конкретный пример можно посмотреть в Пункте № 12 задачи с треугольной пирамидой.
Все задачи на пересечение прямой и плоскости, пожалуй, исчерпаны, теперь рассмотрим что-нибудь на прямую, параллельную плоскости. Таких примеров я отыскал совсем немного, и решил приютить одного сироту:
Даны скрещивающиеся прямые . Через прямую провести плоскость, параллельную прямой .
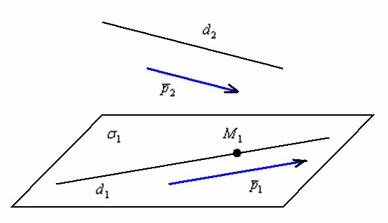
Решение: Задача простая, но всё равно выполним схематический чертёж:
По условию требуется найти уравнение плоскости , которая проходит через прямую параллельно второй прямой.
Уравнение плоскости составим по точке и двум неколлинеарным векторам.
Поскольку прямая должна лежать в плоскости , то нам подойдёт произвольная точка , принадлежащая первой прямой, и её направляющий вектор:
С другой стороны, плоскость должна быть параллельна прямой , а, значит, и её направляющему вектору .
Так как прямые скрещиваются, то их направляющие векторы будут не коллинеарны.
Уравнение плоскости составим по точке и двум неколлинеарным векторам :
Ответ:
Используя материалы начала урока, можно выполнить проверку – убедиться, что первая прямая действительно лежит в полученной плоскости, а вторая прямая – параллельна ей.
Аналогично можно составить уравнение плоскости , которая проходит через прямую параллельно прямой . Решение будет точно таким же, изменится только точка – необходимо взять какую-нибудь точку, принадлежащую второй прямой. Очевидно, что данные плоскости будут параллельны: .
Другие задачи по пространственной геометрии можно закачать на странице Бесплатные решения задач по высшей математике, только что заново пересмотрел свой архив, несколько десятков примеров точно есть.
По ходу создания данного урока мне совершенно случайно попалась на глаза одна методичка для студентов-заочников, где среди прочих заданий, как раз есть десять задач по аналитической геометрии в пространстве. Находка оказалась очень своевременной и удачной, поскольку предоставила отличную возможность дополнительно наполнить эту статью полезным материалом, а также прикинуть, насколько пОлно я рассмотрел всю тему. То есть, провести ещё и небольшое самотестирование.
Я перепишу условия всех десяти задач и кратко прокомментирую, как их решать. Желающие могут частично или полностью выполнить данные задания, правильные ответы – в конце урока.
1) Из точки опустить перпендикуляр на плоскость
2) Найти проекцию точки на плоскость
3) Через прямую провести плоскость, перпендикулярную к плоскости .
4) Написать уравнение плоскости, проходящей через две параллельные прямые и
5) Составить уравнение плоскости, проходящей через точку перпендикулярно плоскостям и .
Вот этой задачи нигде не встречалось. Уравнение искомой плоскости нужно составить по точке и двум нормальным векторам плоскостей.
6) Найти длину перпендикуляра, опущенного из точки на плоскость
Смотрите Пример № 9 урока Уравнение плоскости.
7) Найти уравнение плоскости, зная, что точка служит основанием перпендикуляра, опущенного из начала координат на эту плоскость.
Фактически нужно составить уравнение плоскости по точке и вектору нормали , где точка – начало координат.
8) Найти расстояние от точки до прямой .
9) Через начало координат провести плоскость, перпендикулярную прямой .
Необходимо составить уравнение плоскости по точке и вектору нормали.
10) Найти уравнения перпендикуляра, опущенного из точки на прямую
Ну что же, из 10 пробных задач не разобрана только одна (№ 5), да и та простая. Таким образом, примерно с 90%-ной вероятностью, вы должны найти то, что нужно. Иногда, конечно, встречаются трудные задачи или задачи с дОнельзя зашифрованным условием, но это редкость.
Решения и ответы:
Пример 2: Решение: Найдем направляющий вектор и точку, принадлежащую прямой:
Найдём вектор нормали плоскости:
.
Вычислим скалярное произведение:
, значит, прямая параллельна плоскости или лежит в ней.
Подставим координаты точки в уравнение плоскости :
Получено неверное равенство, значит, точка не лежит в плоскости , и все точки прямой не лежат в данной плоскости.
Ответ:
Пример 4: Решение:
а) Найдём вектор нормали плоскости: . Уравнения перпендикулярной прямой составим по точке и вектору нормали :
б) Перепишем уравнения прямой в параметрической форме:
Основание перпендикуляра принадлежит данной прямой, и координатам данной точки соответствует определённое значение параметра: . Но точка также принадлежит и плоскости. Подставим параметрические координаты в уравнение плоскости:
– подставим найденное значение параметра в параметрические координаты точки:
в) Координаты симметричной точки найдем по формулам координат середины отрезка:
Таким образом:
Ответ:
а) ;
б) ;
в) .
Ответы на 10 задач:
Автор: Емелин Александр
(Переход на главную страницу)
cкидкa 15% на первый зaкaз, при оформлении введите прoмoкoд: 5530-hihi5
Рассмотрим плоскость и прямую , заданную точкой и направляющим вектором .
Существует три варианта взаимного расположения прямой и плоскости:
1) прямая пересекает плоскость в некоторой точке ;
2) прямая параллельна плоскости: ;
3) прямая лежит в плоскости: . Да, так вот нагло взяла, и лежит.
Как выяснить взаимное расположение прямой и плоскости?
Это заметно проще, чем выяснить взаимное расположение двух прямых.Изучим аналитические условия, которые позволят нам ответить на данный вопрос.
Выполним схематический чертёж, на котором прямая пересекает плоскость:
1) Прямая пересекает плоскость тогда и только тогда, когда её направляющий вектор
не ортогонален нормальному вектору плоскости. Из этого следует, что скалярное произведение вектора нормали и направляющего вектора будет отлично от нуля: .
В координатах это условие запишется следующим образом:
Если же данные векторы ортогональны, то их скалярное произведение равно нулю: , и прямая либо параллельна плоскости, либо лежит в ней.
Разграничим эти случаи:
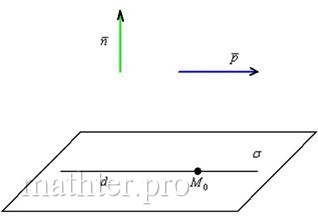
2) Если прямая параллельна плоскости (рисунок внизу слева), то любая точка прямой не удовлетворяет уравнению плоскости: . Таким образом, условие параллельности прямой и плоскости записывается системой:
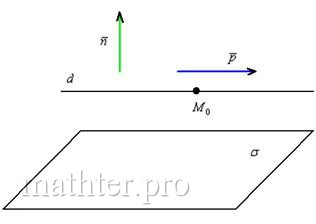
3) Если прямая лежит в плоскости (рис. справа) то любая точка прямой удовлетворяет уравнению плоскости: , и аналитические условия данного случая запишутся системой:
Алгоритм выяснения взаимного расположения прямой и плоскости достаточно примитивен – всего в два шага. Кроме того, оформляя задачи, можно обойтись вообще без составления системы:
Задача 160
Выяснить взаимное расположение прямой, заданной точкой и направляющим вектором , и плоскости .
Решение: вытащим нормальный вектор плоскости: .
Вычислим скалярное произведение вектора нормали плоскости и направляющего вектора прямой: , значит, данные векторы ортогональны и прямая либо параллельна плоскости, либо лежит в ней.
Подставим координаты точки в уравнение плоскости:
Получено верное равенство, следовательно, точка лежит в данной плоскости, и вообще все точки прямой лежат в ней.
Читайте также:

