Высота треугольника кратко и понятно
Обновлено: 04.07.2024
В данной публикации мы рассмотрим определение высоты треугольника, продемонстрируем, как она выглядит в зависимости от вида треугольника, а также перечислим ее основные свойства.
- Определение высоты треугольника
- Высота в разных видах треугольников
- Свойства высоты треугольника
- Свойство 1
- Свойство 2
- Свойство 3
- Свойство 4
Определение высоты треугольника
Высота треугольника – это перпендикуляр, который опущен из вершины фигуры на противоположную сторону.
Основание высоты – точка на противоположной стороне треугольника, которую пересекает высота (или точка пересечения их продолжений).
Обычно высота обозначается буквой h (иногда как ha – это означает, что она проведена к стороне a).
Высота в разных видах треугольников
В зависимости от вида фигуры высота может:
Свойства высоты треугольника
Свойство 1
Все три высоты в треугольнике (или их продолжения) пересекаются в одной точке, которая называется ортоцентром (точка O на чертежах ниже).
Свойство 2
При пересечении двух высот в треугольнике, образуются следующие подобные треугольники:
Свойство 3
Точка пересечения высот в остроугольном треугольнике является центром окружности, вписанной в его ортотреугольник.
![Ортоцентр остроугольного треугольника как центр вписанной в его ортотреугольник окружности]()
Ортотреугольник – треугольник, вершинами которого являются основания высот △ABC. В нашем случае – это △DEF.
Свойство 4
Точки, которые симметричны ортоцентру треугольника относительно его сторон, лежат на окружности, описанной вокруг этого треугольника.
![Симметричность точек на описанной вокруг треугольника окружности относительно его ортоцентра и сторон]()
Примечание: формулы для нахождения высоты треугольника подробно рассмотрены в нашей публикации – “Как найти высоту в треугольнике abc”.
А значит, и прямоугольный треугольник, который поможет тебе решить массу задач!
И самое главное – не нужно ничего запоминать.
Научись выводить и никогда не ошибёшься, сможешь всегда себя проверить и решить любую задачу!
Все в этой статье. Читай и смотри видео.
Высота треугольника — коротко о главном
Высота – линия, проведённая из вершины треугольника перпендикулярно противоположной стороне (прямой, которая эту сторону содержит).
Основанием высоты называют ту точку, в которой высота пересекает противоположную сторону (или её продолжение).
Три высоты любого треугольника пересекаются в одной точке.
Высоты треугольника обратно пропорциональны сторонам, на которые они опущены: \( \displaystyle A_>:B_>:C_>=\frac:\frac:\frac\).
![]()
- Четыре способа вычисления длины высоты, проведенной к стороне BC:
Способ 1. Через сторону и угол треугольника: \( \displaystyle A_>=AC\cdot \sin C=AB\cdot \sin B\).
Способ 3. Через сторону и площадь треугольника: \( \displaystyle A_>=\frac\).
Способ 4. Через стороны треугольника и радиус описанной окружности: \( \displaystyle A_>=\frac\), где \( \displaystyle R\) — радиус описанной окружности.
Читай далее! Здесь не все…
Высота треугольника — подробнее
Высота – линия, проведённая из вершины треугольника перпендикулярно противоположной стороне (прямой, которая эту сторону содержит).
![]()
На этом рисунке \( \displaystyle BH\) – высота.
И тогда получается так:
![]()
Как же решать задачи, в которых участвует высота?
Нужно стремиться применить какие-нибудь знания о прямоугольном треугольнике – ведь где высота – там и прямой угол.
Но для начала решим простенькую задачку на высоту в тупоугольном треугольнике:
В треугольнике \( \displaystyle ABC\) с тупым углом \( \displaystyle C\) проведена высота \( \displaystyle BH\). Найти \( \displaystyle AC\), если \( AB=2\sqrt\), \( BC=\sqrt\), \( BH=2\).
Смотри: из-за того, что угол \( C\) – тупой, высота \( BH\) опустилась на продолжение стороны \( AC\), а не на саму сторону.
![]()
Теперь давай увидим во всём этом два прямоугольных треугольника.
Смотри их целых два:
![]()
Применяем теорему Пифагора к треугольнику \( BCH\):
А теперь теорема Пифагора для \( \Delta ABH\):
Теперь осталось только заметить, что \( AC=AH-CH=6-3=3\).
А теперь давай вернемся к нашим высотам!
В треугольнике проведено две высоты
![]()
Почему бы это? Да очень просто! У них общий угол \( \displaystyle B\) и оба – прямоугольные. Значит, подобны по двум углам.
Здесь тоже подобие по двум углам: \( \angle 1=\angle 2\) (как вертикальные) и по прямому углу.
![]()
Третий, по-настоящему неожиданный факт:
![]()
Вот это уже интереснее, правда? Давай разбираться, почему так.
Читать далее…
Мы хотим постоянно улучшать этот учебник и вы можете нам в этом помочь.
Оформите доступ и пользуйтесь учебником ЮКлэва без ограничений (100+ статей по всем темам ОГЭ и ЕГЭ, 2000+ разобранных задач, 20+ вебинаров-практикумов)В треугольнике проведены три высоты
Как и для медиан, и для биссектрис, для высот треугольника верно следующее утверждение:
В любом треугольнике три высоты или их продолжения пересекаются в одной точке.
Доказывать это утверждение мы здесь, пожалуй, не будем.
1. Треугольник остроугольный – тогда пересекаются сами высоты:
![]()
2. Треугольник тупоугольный – тогда пересекаются продолжения высот:
![]()
Что же полезного мы ещё не обсудили?
Угол между высотами
Давай узнаем, вдруг угол между высотами можно как–то выразить через углы треугольника? Давай рассмотрим остроугольный треугольник.
Итак, нам хотелось бы найти \( \displaystyle \angle \varphi \).
Смотрим на \( \displaystyle \Delta AHC\). Замечаем, что наш \( \displaystyle \angle \varphi \) – внешний угол в этом треугольнике.
Значит, \( \angle \varphi =\angle 1+\angle 2\).
![]()
Чему же равны \( \displaystyle \angle 1\) и \( \displaystyle \angle 2\)?
Конечно, таким же образом из \( \Delta C_>A\) получается, что \( \angle 2=90<>^\circ -\angle A\).
![]()
Теперь \( \angle ~\varphi =\angle ~1+\angle ~2=90<>^\circ -\angle ~C+90<>^\circ -\angle ~A=180<>^\circ -\angle ~A-\angle ~C\).
Но что же это такое? Ведь сумма угла углов треугольника — \( 180<>^\circ \)! Значит, \( \angle \varphi =\angle B\).
Итак, что получилось?
Читать далее…
Мы хотим постоянно улучшать этот учебник и вы можете нам в этом помочь.
Оформите доступ и пользуйтесь учебником ЮКлэва без ограничений (100+ статей по всем темам ОГЭ и ЕГЭ, 2000+ разобранных задач, 20+ вебинаров-практикумов)Остроугольный треугольник и высота
Вернёмся–ка к остроугольному треугольнику. Отметим на рисунке равные углы:
![]()
Что видим теперь? Ещё подобные треугольники!
Как от двух линий вообще могут получиться столько подобных треугольников?!
Но тем не менее…
Видишь, какое богатство? И всё это может быть использовано в задачах!
Ну вот, теперь ты узнал что-то новенькое про высоты треугольника.
Теперь пробуй применять в задачах всё это – и соображение о том, что высота образует прямоугольный треугольник, и простые подобия прямоугольных треугольников, получающихся при пересечении двух высот, и подобие похитрее — которое с косинусом, и то, что угол между высотами равен углу между сторонами…
Главное, ты не старался просто запоминать все эти факты, а осознай, что их можно очень просто вывести.
И тогда, если ты будешь точно знать, например, что две проведённые высоты приносят кучу бонусов в виде всяких подобий, то ты непременно и сам получишь все эти бонусы, а заодно – решение своей задачи!
Бонус: Вебинары из нашего курса подготовки к ЕГЭ по математике
ЕГЭ №6 Все о равнобедренном треугольнике
Очень хороший вебинар, чтобы закрепить решением задач то, что вы изучили в этой статье о высоте.
ЕГЭ №6 Все о прямоугольном треугольнике
Важнейшая тема — прямоугольный треугольник — свойства, теорема Пифагора, тригонометрия.
И уметь решать задачи — чем мы займемся на этом вебинаре.
Наши курсы по подготовке к ЕГЭ по математике, информатике и физике
Курсы для тех, кому нужно получить 90+ и поступить в топовый ВУЗ страны.
![]()
Алексей Шевчук — ведущий курсов
Твоя очередь!
Ты знаешь очень много о высоте треугольника. И вот, что нужно сделать дальше. Практикуйся! Ведь я уверен, что с каждой задачей ты будешь все увереннее применять свои знания!
Высота треугольника – не просто перпендикуляр, длину которого мы используем для нахождения площади, верно? Это кое-что покруче 🙂
А теперь мы хотим узнать твое мнение!
Помогла ли тебе эта статья? Понравилась ли она тебе и все ли было понятно?
Напиши внизу в комментариях!
А если остались вопросы, задай их! Мы непременно ответим тебе!
Удачи на экзаменах!
Добавить комментарий Отменить ответ
Один комментарий
![]()
Александр Кель :
Некоторые комментарии прошлых лет к этой статье:
Дарья Сулейманова
15 января 2018
Сидела и готовилась к зачёту по геометрии около двух часов, заходила на множество разных сайтов. И только на вашем сайте всё написано понятным языком, без заумных терминов. Спасибо!Олеся
06 апреля 2018
Готовится с внуком к ОГЭ. Школу закончила 45 лет назад. Учили в то время просто отлично. Многое помню хорошо, но некоторые нюансы забылись. Ваш сайт очень помог. Все лаконично, по существу и без лишних заумных оборотов. Скачала ла себе на телефон. В свободное время просматриваю. С удовольствием решаю задачи. Спасибо Вам.Ольга
15 февраля 2019
А как бы еще доказать подобие треугольников HcHHa и АНС Можно без окружностейАлексей Шевчук
13 февраля 2020
Дмитрий, угол H — это угол в треугольнике AHC, но в этом треугольнике углы A и С не равны углам A и C треугольника ABC. Чтобы не возникало такой путаницы, важно (а на экзаменах даже обязательно) писать углы полностью (тремя вершинами): ∠AHC = 180 — (∠HAC + ∠HCA); ∠ABC = 180 — (∠BAC + ∠BCA) — и теперь сразу видно, что это не одно и то же.Андрей
08 апреля 2020
Очень доходчивый язык учебника. Как в старой советской школе. Я просто в восторгеАлександр (админ)
08 апреля 2020
Андрей, спасибо большое! Очень приятно слышать! Сравнение лестное! ))Высотой треугольника называется перпендикуляр, опущенный из вершины треугольника на прямую, которая содержит его противоположную сторону.
Каждый треугольник имеет три высоты. Высоту, проведенную из вершины $A$ на сторону $a$, принято обозначать $h_$. Высоты треугольников или их продолжение пересекается в одной точке. В остроугольном треугольнике точка $O$ пересечения высот находится внутри треугольника; в прямоугольном - в вершине прямого угла (совпадает с точкой $C$); в тупоугольном треугольнике - за пределами треугольника. Точка пересечения высот или их продолжений называется ортоцентром.
![]()
![]()
Любую высоту можно найти из соотношений:
Примеры решения задач
Задание. В треугольнике $\Delta A B C$ сторона $A B=2 \sqrt$ мм, $\angle B=45^$. Найти высоту, опущенную на сторону $B C$.
Решение. Обозначим искомую высоту $AH$.
![]()
Для нахождения высоты $AH$ воспользуемся формулой
которая в наших обозначениях запишется следующим образом:
$$A H=A B \cdot \sin \angle B$$
Подставим в последнее равенство исходные данные, получим
$$A H=2 \sqrt \cdot \sin 45^$$
Ответ. $A H=2$ мм
![]()
Мы помогли уже 4 372 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Задание. Одна из сторон треугольника равна 6 см. Найти высоту, опущенную к этой стороне, если площадь треугольника равна 30 см 2 .
Решение. Для нахождения высоты треугольника, воспользуемся формулой
Высотой треугольника, проведённой из данной вершины, называется перпендикуляр, опущенный из этой вершины на противоположную сторону или её продолжение.
![]()
Три высоты треугольника пересекаются в одной точке, называемой ортоцентром треугольника.
Свойства высоты треугольника
- В остроугольном треугольнике высоты пересекаются внутри треугольника; в тупоугольном – вне треугольника; в прямоугольном – в вершине прямого угла.
- В прямоугольном треугольнике катеты являются высотами.
- В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобных исходному.
- В остроугольном треугольнике две его высоты отсекают от него подобные треугольники.
- В равнобедренном треугольнике высота, опущенная на основание, является медианой и биссектрисой.
- В равностороннем треугольнике все высоты являются медианами и биссектрисами.
Примеры решения задач
![]()
![\[BK=AB\sin \angle A=8\cdot \frac<\sqrt</p>
<p>>=4\sqrt \ cm\]]()
![]()
![\[\frac<AK></p>
<p>=\frac\text< >\Rightarrow \text< >B^>=AK\cdot KC=4\cdot 9=36\ cm\]]()
Из прямоугольных треугольников и найдем (используем теорему Пифагора):
![\[AB=\sqrt<A</p>
<p>^>+B^>>=\sqrt=2\sqrt\ cm, \quad BC=\sqrt<C^>+B^>>=\sqrt\ cm\]]()
Далее найдем площадь треугольника :
![\[<<S></p>
<p>_>=\fracAB\cdot BC=\frac\sqrt>=\sqrt\ cm\]]()
![]()
Почти никогда не получится определить все параметры треугольника без дополнительных построений. Эти построения являются своеобразными графическими характеристиками треугольника, которые помогают определить величину сторон и углов.
![]()
Определение
Одной из таких характеристик является высота треугольника. Высота – это перпендикуляр, проведенный из вершины треугольника к его противоположной стороне. Вершиной называют одну из трех точек, которые вместе с тремя отрезками составляют треугольник.
Определение высоты треугольника может звучать и так: высота – это перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону.
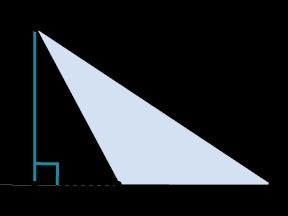
Это определение звучит сложнее, но оно точнее отражает ситуацию. Дело в том, что в тупоугольном треугольнике не получится провести высоту внутри треугольника. Как видно на рисунке 1, высота в этом случае получается внешней. Кроме того, нестандартной ситуацией является построение высоты в прямоугольном треугольнике. В этом случае, две из трех высот треугольника будут проходить через катеты, а третья от вершины к гипотенузе.
![Высота тупоугольного треугольника]()
Рис. 1. Высота тупоугольного треугольника.
Как правило, высоту треугольника обозначают буквой h. Также обозначается высота и в других фигурах.
Как найти высоту треугольника?
Существует три стандартных способа нахождения высоты треугольника:
Через теорему Пифагора
Этот способ применяется для равносторонних и равнобедренных треугольников. Разберем решение для равнобедренного треугольника, а потом скажем, почему это же решение справедливо для равностороннего.
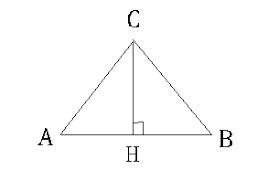
Дано: равнобедренный треугольник АВС с основанием АС. АВ=5, АС=8. Найти высоту треугольника.
![]()
Рис. 2. Рисунок к задаче.
Для равнобедренного треугольника важно знать, какая именно сторона является основанием. Это определяет боковые стороны, которое должны быть равны, а так же высоту, на которую действую некоторые свойства.
Свойства высоты равнобедренного треугольника, проведенной к основанию:
- Высота совпадает с медианой и биссектрисой
- Делит основание на две равные части.
Высоту обозначим, как ВD. DС найдем как половину от основания, так как высота точкой D делит основание пополам. DС=4
Высота – это перпендикуляр, значит ВDС – прямоугольный треугольник, а высота ВD является катетом этого треугольника.
Найдем высоту по теореме Пифагора: $$BD=\sqrt=\sqrt=3$$
Любой равносторонний треугольник является равнобедренным, только основание у него равно боковым сторонам. То есть, можно использовать тот же порядок действий.
Через площадь треугольника
Этим способом можно пользоваться для любого треугольника. Чтобы им воспользоваться, нужно знать значение площади треугольника и стороны, к которой проведена высота.
Высоты в треугольнике не равны, поэтому для соответствующей стороны получится вычислить соответствующую высоту.
Формула площади треугольника: $$S=<1\over2>*bh$$, где b – это сторона треугольника ,а h – высота, проведенная к этой стороне. Выразим из формулы высоту:
Если площадь равна 15, сторона 5, то высота $$h=2*<15\over5>=6$$
Через тригонометрическую функцию
Третий способ подойдет, если известна сторона и угол при основании. Для этого придется воспользоваться тригонометрической функцией.
![Рисунок к задаче]()
Рис. 3. Рисунок к задаче.
Угол ВСН=30 градусам , а сторона BC=8. У нас все тот же прямоугольный треугольник BCH. Воспользуемся определением косинуса угла прямоугольного треугольника. Косинус острого угла – это отношение прилежащего катета к гипотенузе, значит: BH/BC=cos BCH, а угол BCH равен 60 градусам, так как сумма острых углов прямоугольного треугольника равна 90 градусам.
Угол известен, как и сторона. Выразим высоту треугольника:
Значение косинуса в общем случае берется из таблиц Брадиса, но значения тригонометрических функций для 30,45 и 60 градусов – табличные числа.
Что мы узнали?
Мы узнали, что такое высота треугольника, какие бывают высоты и как они обозначаются. Разобрались в типовых задачах и записали три формулы для высоты треугольника.
Читайте также: