Тернарная проблема гольдбаха кратко
Обновлено: 03.07.2024

Проблема Гольдбаха является одной из старейших и наиболее раскрученных задач в истории всей математики.
Было доказано, что эта гипотеза верна для всех целых чисел, меньших 4 × 1018, но остается недоказанной, несмотря на значительные усилия математиков.

Число
Число Гольдбаха является положительным четным целым числом, являющимся суммой пары нечетных простых чисел. Другой формой утверждения гипотезы Гольдбаха является то, что все четные целые числа большие четырех являются числами Гольдбаха.
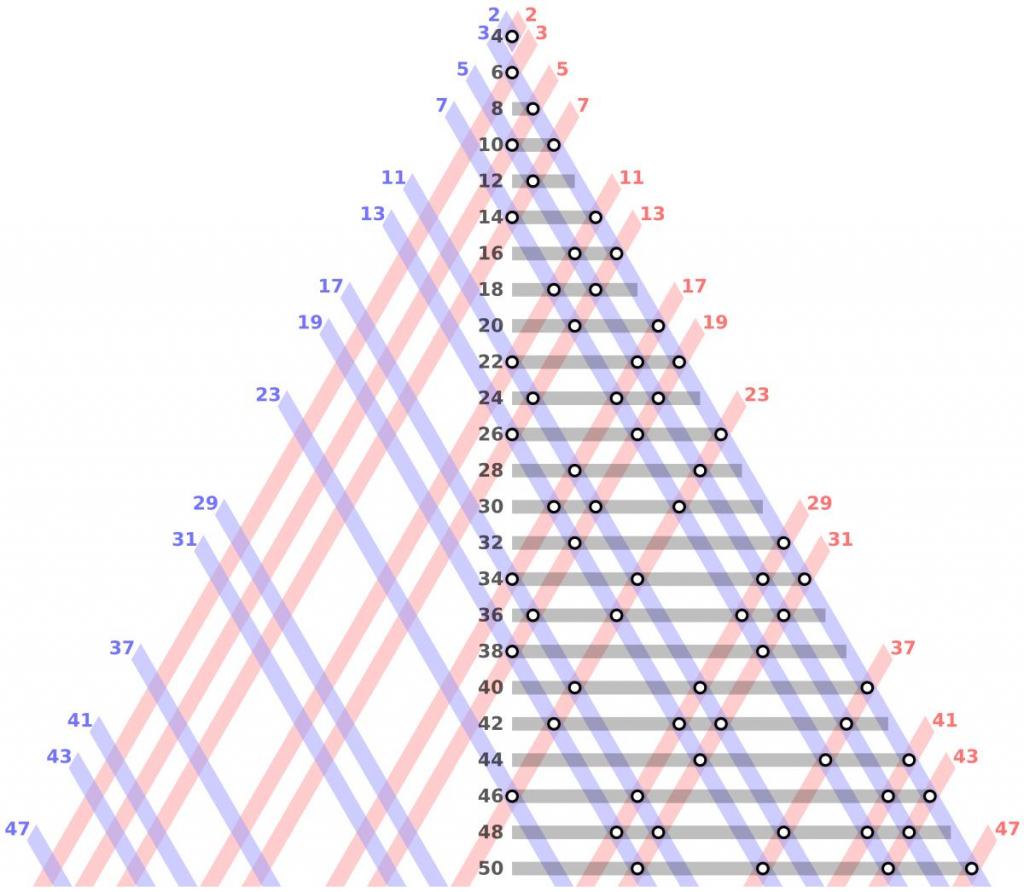
Выделение подобных чисел называется разбиением (или разделом) Гольдбаха. Ниже приведены примеры подобных разделов для некоторых четных чисел:
6 = 3 + 38 = 3 + 510 = 3 + 7 = 5 + 512 = 7 + 5. 100 = 3 + 97 = 11 + 89 = 17 + 83 = 29 + 71 = 41 + 59 = 47 + 53.

Открытие гипотезы
У Гольдбаха был коллега по фамилии Эйлер, который любил считать, составлять сложные формулы и выдвигать нерешаемые теории. В этом они с Гольдбахом были похожи. Эйлер составил похожую математическую загадку еще до Гольдбаха, с которым вел постоянную переписку. Затем он предложил второе предположение на полях своего манускрипта, согласно которому целое число больше 2 можно записать как сумму трех простых чисел. Он считал 1 простым числом.
Проблема Эйлера-Гольдбаха
2 и четные ему числа могут быть записаны как сумма двух простых чисел, что также является гипотезой Гольдбаха. В письме от 30 июня 1742 года Эйлер заявил, что каждое четное целое число представляет собой результат сложения двух простых, он считает это совершенно определенной теоремой, хотя и не может доказать этого.
Третья версия
Проверка
При малых значениях n проблема Гольдбаха (и, следовательно, гипотеза Гольдбаха) может быть проверена. Например, Нильс Пиппинг в 1938 году тщательно проверил гипотезу до n ≤ 105. С появлением первых компьютеров было просчитано еще множество значений n.
Оливейра Сильва совершил распределенный компьютерный поиск, который подтвердил гипотезу для n ≤ 4 × 1018 (и дважды проверил до 4 × 1017) по состоянию на 2013 год. Одна запись из этого поиска состоит в том, что 3 325 581 707 333 960 528 - это наименьшее число, которое не имеет разбиения Гольдбаха с простым числом ниже 9781.
Эвристика
Версия для сильной формы гипотезы Гольдбаха заключается в следующем: поскольку величина стремится к бесконечности с ростом n, мы ожидаем, что каждое большое четное целое число имеет не только одно представление в виде суммы двух простых чисел. Но самом деле очень много подобных представлений. Кем решена проблема Гольдбаха? Увы, все еще никем.

Этот эвристический аргумент на самом деле несколько неточен, поскольку он предполагает, что m по отношению к n является статистически независимым. Например, если m нечетно, то n - m также нечетно, а если m четно, то n - m четно, и это нетривиальное (сложное) отношение, потому что кроме числа 2 только нечетные числа могут быть простыми. Точно так же, если n делится на 3, а m уже было простым, отличным от 3, то n - m также взаимно простое с 3, поэтому с большей вероятностью будет простым числом в отличие от общего числа. Проводя этот тип анализа более тщательно, Харди и Литтлвуд в 1923 году, в рамках своей знаменитой гипотезы простых кортежей Харди – Литтлвуда, внесли вышеупомянутое уточнение во всю теорию. Но решить проблему это не помогло до сих пор.
Сильная гипотеза
Сильная гипотеза Гольдбаха гораздо сложнее, чем слабая гипотеза Гольдбаха. Позже Шнирельман доказал, что любое натуральное число, большее 1, может быть записано как сумма не более чем простых чисел C, где C - эффективно вычисляемая постоянная. Ее пытались решить многие математики, считая и умножая цифры, предлагая сложные формулы и т.д. Но у них никогда ничего не получалось, ибо гипотеза слишком сложная. Никакие формулы не помогали.
Но стоит слегка отойти от вопроса доказательства проблемы Гольдбаха. Константа Шнирельмана - это наименьшее число C с этим свойством. Сам Шнирельман получил C 24 декабря, 2018
В математике проблемой Гольдбаха или гипотезой Гольдбаха называется следующее утверждение:
Любое нечётное число, начиная с 7, можно представить в виде суммы трёх простых чисел.
Вариантом проблемы Гольдбаха (её ещё называют тернарной проблемой Гольдбаха) является проблема Эйлера (или бинарная проблема Гольдбаха), которая до сих пор является одной из старейших нерешённых проблем:
Любое чётное число, начиная с 4, можно представить в виде суммы двух простых чисел.
Проблема Гольдбаха (в совокупности с гипотезой Римана) включена под номером 8 в список проблем Гильберта (1900) и является одной из немногих проблем Гильберта, до сих пор остающихся нерешёнными.
Из справедливости утверждения бинарной проблемы Гольдбаха автоматически следует справедливость тернарной проблемы Гольдбаха: если каждое чётное число, начиная с 4, есть сумма двух простых чисел, то добавляя 3 к каждому чётному числу, можно получить все нечётные числа, начиная с 7. Математики в таких случаях говорят, что утверждение в бинарной проблеме сильнее, чем в тернарной.
Содержание
История исследования
В 1742 году прусский математик Кристиан Гольдбах послал письмо Леонарду Эйлеру, в котором он высказал следующее предположение:
Каждое нечётное число, большее 5, можно представить в виде суммы трёх простых чисел.
Эйлер заинтересовался проблемой и выдвинул более сильную гипотезу:
Каждое чётное число, большее двух, можно представить в виде суммы двух простых чисел.
Первое утверждение называется тернарной проблемой Гольдбаха, второе — бинарной проблемой Гольдбаха (или проблемой Эйлера).
Тернарная проблема Гольдбаха
Это, более слабое, утверждение было доказано для всех достаточно больших чисел И. М. Виноградовым в 1937 году, за что он получил Сталинскую премию и звание Героя Социалистического Труда.
В дальнейшем результат Виноградова многократно улучшали, пока в 1989 году Ванг и Чен не опустили [2] нижнюю грань до e e 11,503 ≈ 3,33339×10 43 000 ≈ 10 43 000,5 , что, тем не менее, по-прежнему находится вне пределов досягаемости для явной проверки всех меньших чисел при современном развитии вычислительной техники.
В 1997 году Дезуйе, Эффингер, те Риле и Зиновьев показали [3] , что обобщённая гипотеза Римана влечёт справедливость слабой проблемы Гольдбаха. Они доказали её справедливость для чисел превышающих 10 20 , в то время как справедливость утверждения для меньших чисел легко устанавливается на компьютере.
Бинарная проблема Гольдбаха
Бинарная проблема Гольдбаха всё ещё далека от решения.

.
В 1930 году Шнирельман доказал, что любое целое число представимо в виде суммы не более чем 800 000 простых чисел. [4] Этот результат многократно улучшался. В 1995 году Ремер (Ramaré) доказал, что любое чётное число — сумма не более чем 6 простых чисел.
В 1966 году Чэнь Цзинжунь (Chen Jingrun) доказал, что любое достаточно большое чётное число представимо или в виде суммы двух простых чисел, или же в виде суммы простого числа и полупростого (произведения двух простых чисел). Например, 100 = 23 + 7 · 11.
На июль 2008 года бинарная гипотеза Гольдбаха была проверена [5] для всех чётных чисел, не превышающих 1,2×10 18 .
Если бинарная гипотеза Гольдбаха неверна, то существует алгоритм, который рано или поздно обнаружит её нарушение. Отсюда следует, что если отрицание бинарной гипотезы Гольдбаха недоказуемо в арифметике Пеано, то гипотеза верна.
Бинарная гипотеза Гольдбаха может быть переформулирована как утверждение о неразрешимости диофантова уравнения 4-й степени некоторого специального вида [6] [7] .
Самые простые математические утверждения иногда бывает сложнее всего доказать. Так, Великая теорема Ферма была окончательно доказана лишь в конце XX века — через несколько сот лет после того, как была сформулирована. Существует еще одно утверждение, чем-то похожее на теорему Ферма, которое математики не смогли доказать до сих пор. Его называют проблемой Гольдбаха, и формулировка этого утверждения предельно проста. В нем всего лишь говорится, что каждое четное число больше 2 можно представить как сумму двух простых чисел. (Поясним: простое число — это число, которое делится только на 1 и на себя само. Так, 2, 3, 5, 7 — простые числа, а 4 (2 х 2), 6 (3 х 2), 9 (3 х 3) — нет.) Впервые это утверждение выдвинул Христиан Гольдбах в 1742 году. Из него следует, что 10 (возьмем пример попроще), как четное число, можно записать в виде суммы 7 + 3, где 7 и 3 — простые числа. Другая формулировка утверждения Гольдбаха, немного менее известная, — что любое нечетное число, большее или равное 9, можно представить в виде суммы трех простых чисел (например, 13 = 7 + 3 + 3 = 5 + 5 + 3).
В 30-е годы XX века группа русских математиков установила, что существует такое конечное n, что любое четное число может быть представлено в виде суммы не более чем n простых слагаемых, а также что гипотеза Гольдбаха верна для большого класса четных чисел. Однако доказательство теоремы до сих пор не найдено.
Почему математики тратят столько времени на решение таких задач, как Великая теорема Ферма или проблема Гольдбаха? Ведь в этом нет практического смысла, из их решения нельзя извлечь никакой выгоды. На мой взгляд, это очень древний и очень свойственный человеческой природе вид деятельности — поиск самоочевидной, бесспорной истины. Философы тысячелетиями ищут истину. Математики надеются обнаружить такие истины, работая с системами, построенными на чистой логике. И то, что эти доказательства столь трудно достижимы, наверное, объясняется скорее самой природой логики, невозможностью найти истину в этом ненадежном, изменчивом мире, а не свойством математики как таковой.
Немецкий математик. Родился в Кёнигсберге в Пруссии (ныне Калининград, Россия). В 1725 году стал профессором математики в Санкт-Петербурге, тремя годами позже приехал в Москву в качестве домашнего учителя для будущего царя Петра II. Во время путешествий по Европе Гольдбах познакомился со многими ведущими математиками своего времени, включая Готфрида Лейбница, Абрахама де Муавра и семью Бернулли. Многие его работы выросли из переписки с великим швейцарским математиком Леонардом Эйлером (Leonhard Euler, 1707–83). Утверждение, которую мы теперь называем проблемой Гольдбаха, впервые было выдвинуто в 1742 году в письме Гольдбаха к Эйлеру.
Читайте также:

