Теория кос в математике кратко

Обновлено: 28.06.2024

Для осуществления обозначенной цели служат следующие задачи:

1. изучить теорию кос, историю возникновения и развития;

2. изучить теорию узлов, историю возникновения и развития;

3. изучить теорему Артина и представление Бурау.

Глава 1. Теория узлов

История развития и возникновения узлов

Узел галстука, узлы корабелов и альпинистов, гордиев узел, клубок змей, петля палача. Узлы — это и обиходные предметы, и символы сложности. Узлы — точнее, математическая теория узлов — интересует многих биологов, химиков, физиков. Узлы повсеместно использовались уже со времен античности. Это объясняется их важной технологической ролью, особенно в мореходстве и строительстве. Но появление веревок и узлов произошло раньше, в доисторические времена, и предшествовало изобретению топора, лука, колеса.

Сегодня мы применяем узлы, даже не задумываясь, что их возраст исчисляется тысячелетиями. Такие узлы, как выбленочный, прямой и беседочный (рис.1), служили жителям Древнего Египта еще пять тысячелетий назад.

Например, выбленочный узел был обнаружен на двери третьего помещения гробницы фараона Тутанхамона.

Рис.1

Прямой (или квадратный) узел, хорошо известный в Древнем Египте, был широко распространен в быту древних греков и римлян.

Лучшие из узлов пережили века, переходя от поколения к поколению. Существует изображения более 700 различных узлов.

Теорией узлов занимались не только математики. Большая заслуга принадлежит здесь физикам – начиная от лорда Кельвина, предложившего описывать химические элементы узлами, и кончая Э. Виттеном – единственным физиком – лауреатом филдсовской медали. Многие инварианты узлов (полином Джонса, а также инварианты конечного порядка, называемые также инвариантами Васильева) физики пытаются использовать в своих исследованиях.

Понятие узлов.

Узел - это некая абстракция, которая рассматривается не как веревка и шнур, а как бесконечно тонкая, гибкая и растяжимая нить. При рассмотрении математического узла нужно либо как-то зафиксировать его концы, либо соединить их.

Есть много видов нетривиальных узлов, например, узел на рис.2 называется трилистником, узел на рис.3 – восьмеркой.

Рис.2 Рис.3

Дадим определение эквивалентности узлов. Узел – это ломаная. С ломаной можно производить элементарные операции: (рис.4)

1) два последовательных звена АВ и ВС ломаной заменить звеном АС;

2) звено АС заменить двузвенной ломаной АВUВС

Рис.4

Обе операции разрешены, если только треугольник АВС не пересекается (в пространстве) ни с какими другими кусками нашего узла.

Два узла называются эквивалентными, если их можно элементарными операциями превратить в совершенно одинаковые узлы.

Деформируя объемлющее пространство R 3 мы также деформируем и узел. Два узла называются изотопными, если один из них может быть продеформирован в другой посредством диффеоморфизма объемлющего пространства на себя, сохраняющего ориентацию.

Для того чтобы показать, что два узла не являются изотопными, достаточно найти инвариант узлов, который принимает разные значения на этих узлах.

Узлы кодируются следующим образом. Сначала фиксируем узел, т.е образ отображения. Рассматривает некоторую плоскость и проекцию узла на нее. Без ограничения общности можно считать, что проекция узла на плоскость представляет собой вложенный конечный четырехвалентный граф, который является образом гладкого погружения окружности в плоскость. Часть этого узла называется ветвью. Каждая вершина графа проекции, которая называется перекрестком, оснащена структурой. Пусть a и b – две ветви узла, проекции которых пересекаются в какой-либо точке. Так как a и b не пересекаются в плоскости, то два прообраза этой точки имеют различные координаты. Таким образом, мы можем сказать, какая ветвь проходит сверху, т.е. образует переход, а какая – снизу, т. е. образует проход. Ребра переходов изображаются сплошными линиями, а ребра проходов имеют разрыв в перекрестке.(рис. 5)

Такое изображение узла называется плоской диаграммой узла.

Рис.5

Четырехвалентный граф проекции без указания структуры проходов и переходов называется тенью узла. Сложностью узла называется минимальное количество перекрестков диаграмм узлов.

У каждого узла есть зеркальное отражение, т.е. узел, полученный из него отражением в некоторой плоскости. Узел называется зеркальным, если он изотопен своему зеркальному отражению.

Теорема об узлах.

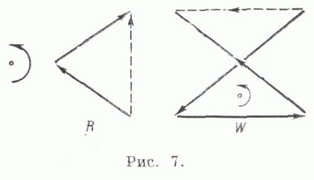
А можно ли умножать узлы? Если считать узлы кривыми, концы которых уходят в бесконечность, то произведение узлов a и b – это просто нить, на которой завязан сначала узел a, затем узел b.(рис.6)

Рис.6

Это умножение, как и умножение кос, ассоциативно: для любых узлов a,b и c

Тривиальный узел, т.е. вертикальная прямая является единичным элементом (рис.7)

Рис.7

В отличие от кос, ни один нетривиальный узел не имеет обратного: если мы завяжем на нити два узла, а затем потянем за концы, узлы не развяжутся.

Два узла, завязанных на одной веревке можно переставлять. Пусть на нити завязан сначала узел a, затем узел b (рис.8)

Рис.8

Рис.9

Потом заключим этот узелок в маленький стеклянный шарик и будем двигать его вверх по нити. (рис.10)

Рис.10

В итоге этот шарик окажется наверху, и его можно превратить опять в узел b. Таким образом, умножение узлов коммутативно:

a∙b=b∙a, отсюда следует теорема об узлах:

Узлы образуют ассоциативную и коммутативную систему относительно умножения. В этой системе есть единичный элемент, но нет обратных элементов.

Движения Рейдемейстера

Любая деформация плоскости, неизменяющая взаимное расположение перекрестков, не меняет изотопического типа зацепления. При этом существуют еще три движения, называемые движениями Рейдемейстера, которые обозначаются Ω₁, Ω₂, Ω₃. Эти движения не изменяют расположение перекрестков и не меняют изотопического типа зацепления. (рис.11)

Рис.11

Каждое из трех движений Рейдемейстера изменяет диаграмму зацепления только внутри маленькой области. Это означает, что вне этой области диаграмма зацепления остается неизменной, а внутри изменяется так, как показано на рис.11 (сверху). Теперь можно показать, что узел, показанный на рис. 11 ( снизу слева), тривиален.

Глава 2. Теория кос

История развития и возникновения кос

Коса – это какое-то количество нитей, которые переплетаются между собой.

Теория кос - наука, возникшая в 20-х годах 20-ого века. Исследования на эту тему еще не завершены.

Основания теории кос были построены благодаря азарту и настойчивости немецкого математика Эмиля Артина. Первоначально косы были предложены Артином в качестве математической модели для текстильной промышленности. Теория кос занимает важное место в комплексном анализе, комбинаторике, квантовой механике и квантовой теории поля.

Понятие кос

Можно получить узел из косы с помощью операции замыкания, которая состоит в том, чтобы присоединить верхние концы прядей к нижним концам (рис. 12 узел – трилистник)

Рис.12

Рис. 13 показывает, что не всегда таким образом можно получить узел. Замыкание косы может также оказаться зацеплением, т. е. состоять из нескольких кусков (из нескольких кривых, в отличие от узла, по определению, состоящего лишь из одной кривой).

Рис.13

Какие узлы можно получить таким образом? Ответ, полученный американским математиком Александером в 1923 г.,объясняет важность кос в теории узлов: можно получить любой узел!

Теорема Александера:

Каждый узел может быть получен как замыкание некоторой косы.

(Фактически Александер показал, что это утверждение верно для зацеплений, частным случаем которых являются узлы.) Вероятно, Александер надеялся, что его теорема послужит решающим шагом классификации узлов. Действительно, косы являются значительно более простыми объектами, чем узлы; множество кос обладает весьма прозрачной алгебраической структурой, позволяющей их классифицировать.

Следовательно, мы можем получить классификацию узлов, основываясь на классификации кос.

Вернемся к изучению кос. Прежде всего мы определим операцию произведения на множестве кос c одним и тем же количеством нитей n.

Эта операция заключается в последовательном связывании кос (соединении верхних концов нитей второй косы с нижними концами нитей первой), как на рис.14.

Рис.14

Сейчас мы убедимся, что произведение кос обладает многими свойствами обычного произведения чисел. Прежде всего, имеется единичная коса (обозначаемая e), т. е. коса, которая, как число 1, не изменяет то, что на нее умножается. Это тривиальная коса, нити которой спадают вертикально, не переплетаясь. Действительно, прикрепление снизу тривиальной косы к данной косе приводит лишь к удлинению ее нитей и не изменяет тип косы.

Во-вторых, для каждой косы b существует коса, называемая обратной 1-и обозначаемая b , такая, что ее произведение с b дает тривиальную косу,

b · 1- b = e (так же как для каждого числа n его произведение с обратным числом 1/n , равно единице.)

Эта коса получается, если взять отражение данной косы в горизонтальном зеркале.

Действительно, каждый перекресток уничтожается своим зеркальным изображением, таким образом, все перекрестки взаимно уничтожаются попарно шаг за шагом, начиная с середины косы-произведения.(рис.15)

Рис.15

Третье свойство, общее у кос и у чисел, — свойство ассоциативности произведения: всегда выполняется равенство (a · b) · c = a · (b · c).

Когда некоторое множество снабжено операцией, обладающей тремя свойствами, то это и есть группа.

Следовательно, множество кос с n нитями образует группу. Эту группу мы будем обозначать через Bn.

Отметим сразу же, что группа кос Bn (для n > 2) — в отличие от чисел — не коммутативна: произведение двух кос зависит в общем случае от порядка множителей.

Существование произведения кос позволяет заменять рисунок, изображающий косу, некоторым словом — алгебраическим представлением этой косы.

Действительно, двигаясь сверху вниз вдоль косы, наша коса — последовательное произведение кос с одним перекрестком в каждой ( рис. 16); они называются элементарными косами и обозначаются (в случае кос с n нитями) - b₁,b₂,…,b_n_-1.

Невозможные фигуры - это пленительные объекты, имеющие отношение к изобразительному искусству, психологии и математике.[1] Лайонел и Роджер Пенроузы (отец и сын) изобрели невозможный треугольник, или трибар (tribar), в 1958 году.[2] (рис. 1) Фигура называется невозможной, когда "восприятие сообщает о противоречии фигуры, но не позволяет разрешить это противоречие, представив непротиворечивую фигуру".[3] Объект, представленный на рис. 1 является невозможной фигурой, так как наш мозг пытается интерпретировать ее как трехмерную (3D) фигуру в евклидовом пространстве с прямыми ребрами и плоскими гранями, вместо, к примеру, двухмерного объекта, нарисованного на бумаге (что я является вполне возможным).

Невозможные фигуры вдохновили ученых и исследователей на написание более сотни научных статей (см. библиографию Зенона Кульпы [4]), а также голландского художника М.К. Эшера [5] на создание его знаменитых гравюр.

Рис. 2. (см. [6])

Определим мультибар как многогранник [7][8], состоящий из набора брусков прямоугольного сечения, составляющих фигуру правильного многоугольника. Одним из примеров может служить трибар Пенроузов (рис. 1). Но также из брусков могут быть составлены и другие трех-брусочные конструкции на основе правильного треугольника. Некоторые примеры таких конструкций представлены на рис. 3.

По интуиции, первые две фигуры выглядят невозможными, а третья - возможной. Рассмотрим теперь семейство фигур, производных от трибара (см. рис. 4).

Изобразим на фигурах с рис. 4 скрытые ребра пунктиром (см. рис. 5).

Сразу можно обратить внимание, что на представленных фигурах имеются ребра двух видов: продольные грани (изображены синим цветом) и поперечные (изображены зеленым цветом). Данная работа была создана под влиянием работ Т.М. Кована (T.M. Cowan) [9][10], который использовал теорию кос (braid theory) для анализа невозможных фигур. Он описывал каждую сторону невозможного многогранника как линию косы. Мы находим более естественным описывать каждое продольное ребро невозможной фигуры как линию косы. Мы намереваемся показать, что теории кос недостаточно для представления мультибара. Необходимо связать косу в узел или соединение надлежащим образом, чтобы мультибар имел только единственное представление.

Рассмотрим основные положения теории кос. n-элементная коса состоит из n линий, направленных сверху вниз. Ни одна из линий не может быть направлена вверх. Линии могут пересекаться друг с другом, и в каждом пересечении та линия, которая расположена позади другой отмечается разрывом. Мы используем обозначения, введенные П. Дехорноем (P. Dehornoy) в работе [11], используя символы в нижнем и верхнем регистре в отличие от использования обозначений s_i и s_i -1 , для обозначения пересечений (см. рис. 5).

Пересечения в косах формируются в группы посредством операции соединения при помощи следующих соотношений.

Первое соотношение (ac = ca) верно для любых двух символов расположенных друг от друга на расстоянии не менее 2 символов внутри алфавита. Второе соотношение (aba = bab) верно для любых двух последовательных символов алфавита. Также необходимо ввести правило инверсии для любой группы, то есть aA = bB = cC = тривиальность. Тривиальность n-элементной косы означает, что она соответствует косе из n непересекающихся линий.

Рассмотрим теперь один из углов многогранника с рис. 5. Соответствующая этому углу коса представлена на рис. 8.

Четырехэлементные косы, соответствующие трибару, невозможному квадрату и невозможному пентагону имеют следующий вид соответственно bacbacbac, bacbacbacbac, и bacbacbacbacbac.

Следует обратить внимание, что многогранники представленные на рис. 4 могут быть изображены и в виде, представленном на рис. 9.

Тогда один угол каждого из таких многогранников будет представлен следующей косой (см. рис. 10).

Четырехэлементные косы, соответствующие трибару, невозможному квадрату и невозможному пентагону, представленным на рис. 9, будут иметь следующий вид соответственно acbacbacb, acbacbacbacb, и acbacbacbacbacb.

Мы подошли вплотную к понятию замкнутой косы, представленной на рис. 11. Замыкание косы преобразует ее в узел (или соединение), который является представлением замкнутой линии (или нескольких линий) в трехмерном пространстве.

Теорема Маркова [12] гласит, что различные косы после замыкания соответствуют одному и тому же узлу, если они преобразуются к нему посредством конечного числа изменений двух видов:

Объединение (в случае рассмотрения цепочек пересечений мультибаров мы перемещаем пересечение b с одного конца косы в другой по линии соединения);
Изменение, при котором к косе добавляется линия, образуя пересечение между двумя крайними линиями. (Данное изменение не входит в контекст решаемой задачи, так как косы мультибаров ограничены четырьмя линиями)

Таким образом, видно, что для мультибаров, представленных на рис. 4 существует только одно представление узла, независимо от угла обзора фигуры.

Преимущество использования узлов перед использованием кос при анализе невозможных фигур более ярко видно, если мы будем рассматривать "магическую пентаграмму" (рис. 12 слева), представленную в работе Л. Саллоуса (Sallows)[13] и на последней странице книги Ф.Дж.Светца (F.J. Swetz)[14]. Представленный вариант пентаграммы в виде брусков удовлетворяет нашему определению мультибара.

Четырехэлементная коса, соответствующая пентаграмме, bacbacbacbacbac (или acbacbacbacbacb в зависимости от угла обзора) неотличима от косы невозможного пентагона с рис. 4. В противоположность узлу, соединение, соответствующее невозможной пентаграмме, значительно отличается от соединения, соответствующего невозможному пентагону, так как в этом случае принимается во внимание расположение брусков в пространстве друг относительно друга. В этом случае, необходимо рассматривать сопровождающее соединение, дружественный узел которого изображен на рис. 12 справа. Это дружественное соединение может быть нетривиальным, так как дружественный узел является нетривиальным.

Если изобразить (см. рис. 13) скрытые ребра треугольника (см. рис. 3), который является возможной фигурой, легко увидеть, что соответствующее ему соединение является тривиальным четырехэлементным соединением.

В заключение, мы подошли к формулировке критерия, в соответствии с которым, можно определить, является ли мультибар невозможной фигурой: "Если узел или соединение, соответствующее мультибару, отличается от тривиального четырехэлементного соединения, тогда мультибар является невозможной фигурой.

Большое спасибо Френсису Бейкенхауту (Francis Buekenhout), который открыл мне "невозможную пентаграмму" и побудил написать данный текст.

Глава 36. ТЕОРИЯ ГРУПП И КОСЫ

Трое программистов — Эймз, Бейкер и Кумбс — хотят решить, кому из них платить за пиво. Разумеется, они могли бы бросить монетку, но предпочитают случайный выбор, основанный на игре, которая состоит в блуждании по некоторой сети линий. На листе бумаги проведены три вертикальные линии (назовем их основой).

Один из программистов, держа лист так, чтобы его друзья не видели, что он делает, обозначает эти линии наугад буквами А, В и С (рис. 180, а).

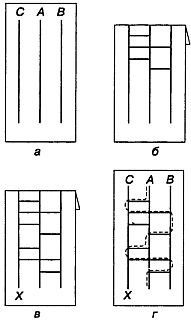
Верхний край листа он загибает так, чтобы буквы не были видны. Второй программист наугад проводит ряд горизонтальных линий (назовем их утком), каждая из которых соединяет какие-нибудь две вертикальные линии (рис. 180, б). Третий программист добавляет еще несколько горизонтальный линий, а у одной из вертикальных линий снизу ставит букву X (рис. 180,в).

Лист бумаги разворачивают. Эймз ставит свой палец в верхнюю точку линии А и начинает обводить ее сверху вниз. Дойдя до начальной или конечной точки линии утка (если точка пересечения вертикальной линии с линией утка лежит внутри горизонтального отрезка, Эймз ее пропускает и следует дальше), он поворачивает и проходит всю эту линию до другого ее конца, после чего снова поворачивает и продолжает спускаться вниз до тех пор, пока снова не встретит начальную или конечную точку другой линии утка. Так продолжается, пока он не достигнет нижней точки какой-нибудь вертикальной прямой. Если его путь (на рис. 180,г он показан пунктирной линией) заканчивается не в точке X, то за пиво платит не он. Затем точно таким же способом по сети прямых путешествуют Бейкер и Кумбс. Путь Бейкера заканчивается в точке X, поэтому за пиво приходится платить ему. Каким бы ни было число линий основы (вертикальных прямых), независимо от того, как проведены линии утка (горизонтальные прямые), пути игроков всегда заканчиваются на различных прямых, и никакие два маршрута никогда не приводят к одной и той же линии.

При более подробном рассмотрении этой игры выясняется, что в основе ее лежит одна из простейших групп — так называемая группа перестановок трех элементов. Что же такое группа? Это некая абстрактная структура, состоящая из множества элементов (а, Ь, с….), относительно природы которых не делается никаких предположений, с единственной бинарной операцией (ее мы обозначим символом о), сопоставляющей каждой паре элементов множества некоторый третий элемент. Чтобы такая структура составляла группу, должны выполняться следующие четыре условия:

(а о Ь) о с = а о (b о с).

а о е = е о а = а.

4. Для каждого элемента а существует обратный элемент а', такой, что

а о а' = а' о а = е.

Если помимо только что названных четырех условий операция подчиняется еще и коммутативному закону:

а о Ь = b о a,

то группа называется коммутативной, или абелевой.

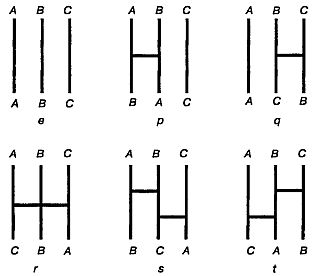
Рис. 181 Шесть элементов группы, возникающей в задаче о блуждании по сети линий.

Полное описание строения этой группы видно из рис. 182.

Рис. 182 Результаты последовательного выполнения двух преобразований из группы, возникающей в задаче о блуждании по сети линий.

Что получится, если вслед за преобразованием r проделать преобразование s? Найдем букву r среди букв, выписанных слева от таблицы, и букву s среди букв, выписанных сверху. На пересечении r-й строки и s-ro столбца стоит буква р. Иначе говоря, добавив к горизонтальным линиям преобразования r горизонтальные линии преобразования s, мы получим такую же перестановку нижних концов вертикальных линий А, В и С, какая возникает, если провести горизонтальные линии одного лишь преобразования р. Эта чрезвычайно простая группа возникает во многих местах. Например, если обозначить тремя различными буквами вершины равностороннего треугольника, а затем произвести над ним все повороты и отражения, в результате которых он совмещается с самим собой, то окажется, что различных преобразований имеется только шесть и они образуют в точности такую же группу, как только что описанная.

Не обязательно вникать в тонкости теории групп, чтобы интуитивно понять, что, блуждая по сети, никакие два игрока не могут закончить свой путь на одной и той же вертикали. Вообразим, что три вертикальные линии — это просто-напросто три веревки. Каждый раз, проводя горизонтали, мы как-то переставляем нижние концы вертикалей, но точно такого же результата мы достигнем, если перевьем две веревки так, как это делают с прядями волос при заплетании косы. Ясно, что, как бы вы ни заплетали косу и какой бы длинной она ни была, дойдя до ее конца, вы всегда сможете различить все три пряди.

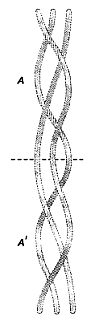
Рис. 183 Коса А — зеркальное отражение косы А'.

Теория кос имеет самое непосредственное отношение к необычной игре, изобретенной все тем же датским поэтом, писателем и математиком Питом Хейном. Вырежьте из плотного картона кусочек в форме геральдического щита (рис. 184).

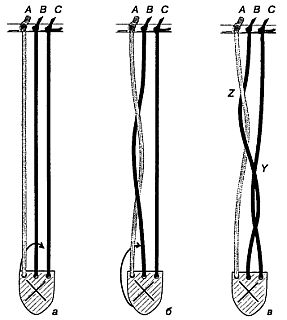
Рис. 184 Полный оборот подвески а по стрелке порождает косу б. Перевернув подвеску по стрелке еще раз, мы получим косу в.

Этот кусочек мы будем называть подвеской. Поскольку нам понадобится различать стороны подвески, их лучше всего раскрасить в разные цвета или одну из сторон пометить буквой X. У прямого края подвески проделайте три отверстия и, пропустив в каждое из них по отрезку тяжелого, но гибкого шнура длиной около 60 см, завяжите шнурки узлом (великолепно подходит для этих целей крученый шнур, из которого делают пояса). Другой конец каждого шнура привяжите к какому-нибудь неподвижному предмету, например к спинке стула.

Хейн впервые услышал об этой теореме в начале тридцатых годов на одном семинаре в Институте теоретической физики Нильса Бора, когда П. Эренфест обсуждал ее в связи с какой-то проблемой квантовой теории. С помощью ножниц, принадлежавших супруге Бора, и нескольких веревочек, привязанных к спинке стула, Хейну и другим участникам семинара удалось найти доказательство этой теоремы. Позднее Хейну пришло в голову, что вращающееся тело и окружающая его вселенная входят в задачу симметрично, поэтому симметричную модель можно было бы построить очень просто, привязав по подвеске к каждому концу шнура. Имея такую симметричную модель, можно вдвоем играть в топологическую игру. Каждый участник берет свою подвеску; между подвесками протянуты три шнура. Один из игроков заплетает косу, а второй, расплетая ее, засекает необходимое для этого время, затем игроки меняются ролями. Тот, кто расплетет косу быстрее, считается победителем.

Почему между четным и нечетным числом полных оборотов подвески существует такое различие? На этот весьма непростой вопрос трудно ответить, не вдаваясь более глубоко в теорию групп.

Некоторое представление о причинах такого различия можно получить, заметив, что два поворота в противоположных направлениях—это то же самое, что ни одного поворота. Если два оборота почти противоположны и отличаются только тем, что при совершении их подвеска была пропущена между различными парами шнуров, то косу можно расплести, продев подвеску между шнурами так, чтобы уничтожить это различие. Пользуясь теорией кос, можно доказать, что при нечетном числе оборотов подвески пряди распутать нельзя.

Заплетать косы, поворачивая подвеску наугад четное число раз, а затем быстро расплетать их — занятие увлекательное. На рис. 185 показаны три простые косы, каждая из которых заплетена лишь двумя полными оборотами подвески.

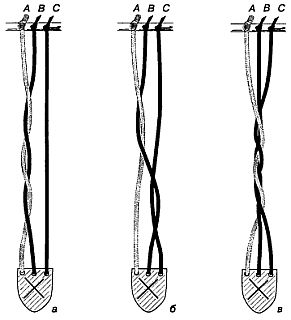
Рис. 185 Три задачи на расплетание кос.

Косу в случае а получили, дважды пропустив подвеску между шнурами В и С (оба раза от себя); в случае б — продев подвеску между шнурами В и С от себя, а затем между шнурами А и В в обратном направлении. Коса в случае в заплелась от того, что подвеску два раза повернули слева направо вокруг вертикальной оси. Читателю предоставляется самому найти лучший способ расплетания каждой из этих кос.

Вместо трех отдельных шнуров Хейн рекомендует брать один длинный шнур. Шнур нужно пропустить через первое отверстие первой подвески и привязать к ней, чтобы он не выскальзывал. Затем его нужно продеть сквозь первое отверстие второй подвески и, пропустив в обратном направлении через среднее отверстие все той же второй подвески, продеть через среднее отверстие первой подвески, после чего продеть в обратном направлении через третье отверстие первой подвески и, продев сквозь третье отверстие второй подвески, завязать свободный конец шнура узлом. Шнур свободно может проскальзывать в отверстия, что облегчает все манипуляции по сравнению с конструкцией, в которой используются три отдельных шнура. Один читатель сообщил нам, что он соединил свои подвески тремя отрезками гибкого шнура и обнаружил, что это также облегчает все манипуляции. Игру можно усложнять, вводя все новые и новые шнуры, но и при трех шнурах она весьма непроста.

Из рис. 182 видно, что описывающая танглоид группа неабелева (то есть некоммутативна). Таблицы для абелевых групп симметричны относительно диагонали, идущей из левого верхнего в правый нижний угол. Иначе говоря, треугольные части таблицы, лежащие по обе стороны этой диагонали, служат зеркальным отражением одна другой.

Ответы

1. Пропустите подвеску под шнуром С справа налево, а затем под шнурами А и В слева направо.

2. Пропустите подвеску под серединой шнура В слева направо.

3. Пропустите подвеску под всеми шнурами слева направо.

Примечания:

'American Mathematical Monthly, 64, 1957, p. 143.

Чеширский Кот — один из персонажей известной сказки Льюиса Кэрролла "Алиса в Стране Чудес"

Artin E. Theory of Braids:.Annals of Mathematics, 48, № 1, January 1947, pp. 101–126.

Представлено краткое содержание работы НОУ "Теория кос и узлов".

Вложение	Размер
Работа НОУ- диплом 1 степени городской конференции НОУ "Эврика"	710.79 КБ

Предварительный просмотр:

Китаев Дмитрий, Бурмистрова Татьяна.

Теория кос и узлов – сравнительно молодой и интенсивно развивающийся раздел математики. Математики впервые заинтересовались косами и узлами лишь в XIX веке и с того времени теория кос и узлов обрела статус самостоятельного раздела математики. Изучением кос и узлов занимались такие великие ученые, как Эмиль Артин (создатель теории кос), Дж. Конвей, Дж. Александер, В. Джонс, В. Тураев, А. Решетихин, Л. Кауфман и другие.

Объектом данного исследования является теория кос и узлов.

Одним из достоинств этой науки является доступность её предметов исследования: достаточно взять любую бечёвку и соединить её концы, получится гладкая замкнутая кривая без самопересечения - узел, а конечный набор замкнутых непересекающихся ориентированных ломаных в пространстве будет зацеплением .

В работе показано, как математические методы, позволяют решать основную проблему теории кос и узлов –проблему классификации, сравнения и распутывания кос и узлов.

Косу представим так: в верхний и нижний край вертикальной плоскости вобьем по n гвоздиков ( n =1,2,3…) – каждый из гвоздиков вертикального основания соединим нитью с одним из гвоздиков нижнего; нити попарно не пересекаются и всё время должны спускаться вниз. Получили косы: . К 1 — «девичья коса *; К 2- тривиальная коса (аналог 1), К 4 — крашеная коса; К 5 — циклическая коса. ( рис.1).

Косы с одинаковым числом нитей можно умножать: верх второй косы прикладывается к низу первой и соответствующие нити склеиваются. (рис.2). Умножение кос обладает следующими свойствами чисел :

для любых трех кос выполняется ассоциативный закон; .

для косы К верно: 1 . К=К . 1=К ; К -1 . К=К . К -1 =1, где коса К -1 - коса, обратная косе К.

Проблему классификации кос можно решать с помощью

основных соотношений теории кос:

S j S j - 1 = S j -1 S j = 1 , S j . 1=1 . S j =S j (j=1, 2,…, n-1).

S i S j =S j S i при i-j 2 (i,j=1,2,…, n-1).

Пусть S i S j = К1, К2 = S j S i при |i-j|>=2. Получаем, что в обеих косах нить, вышедшая из позиции i, попадает в позицию (i+1), из (i+1) - в i, из j - в (j+1), из (j+1) - в j, так как |i-j|>=2. Если в диаграмме одной из кос нить, выходящая из позиции i, была сверху (снизу) нити, выходящей из позиции (j+1), то и во второй косе будет то же самое, там как нить, перейдя из позиции i в (i+1) (или из j в (j+1)), не может перейти в другую позицию, потому что (i+1) не может равняться j (или (j+1) не может равняться i). Следовательно, К 1 =К 2 , что и требовалось доказать.

3. Соотношения сплетения SiSi+1Si Si+1 (i=1, 2, …, n-2).

Любая коса представляется в виде произведения элементарных кос S 1 ,S 2 ,…,S n-1 и обратных к ним, например,

K 1 =S 1 S 2 -1 S 1 S 2 -1 S 1 S 2 -1 . , K 3 =S 2 S 1 S 3 -1 S 1 -1 S 3 S 2 -1 S 1 S 3 S 1 -1 S 3 -1 .

1. Докажем, что S 1 -1 *S 2 -1 *S 1 -1 = S 2 -1 *S 1 -1 *S 2 -1.

Пусть K 1 =S 1 -1 *S 2 -1 *S 1 -1 , K 2 =S 2 -1 *S 1 -1 *S 2 -1 .

Тогда K 1 -1 =S 1 *S 2 *S 1 , K 2 =S 2 *S 1 *S 2 .

По тождеству 3 K 1 -1 =K 2 -1 . Значит, по тождеству 1 К 1 =K 2 , что и требовалось доказать.

2. Докажем, что S 1 *S 2 *S 1 *S 2 -1 *S 1 -1 = S 3 *S 1 *S 3 -1 *S 1 -1 *S 2 .

S 1 *S 2 *S 1 *S 2 -1 *S 1 -1 =S 3 *S 1 *S 3 -1 *S 1 -1 *S 2 ; S 2 *S 1 *S 2 *S 2 -1 *S 1 -1 =S 1 *S 3 *S 3 -1 *S 1 -1 *S 2 ; S 2 *S 1 *S 1 -1 =S 1 *S 1 -1 *S 2 ; S 2 =S 2 , что и требовалось доказать.

3. Докажем тривиальность косы К 3.

K3=S2(S1S3 -1 )S1 -1 S3S2 -1 S1(S3S1 -1 )S3 -1 =S2S3 -1 (S1S1 -1 )S3S2 -1 (S1S1 -1 )(S3S3 -1 )=

=S2S3 -1 . 1 . S3S2 -1 . 1 . 1 =S 2 (S 3 -1 S 3 )S 2 -1 =S 2 S 2 -1 =1, что и требовалось доказать.

Узел - замкнутая кривая без самопересечения , узел можно описать двумерной диаграммой .

Конечный набор замкнутых непересекающихся ориентированных ломаных в пространстве называется зацеплением .

Два узла называются эквивалентными , если узел, сжимая, растягивая, двигая в пространстве (без разрывов и склеек), можно превратить в другой.

Главной проблемой теории узлов является поиск инварианта, препятствующего распутыванию.

Любой узел является замыканием некоторой косы.

Возьмём косу, изогнём её дугой и склеим конец с началом, получится узел. Но замыкание разных кос не всегда приводит - к разным узлам. Например, коса из трёх нитей не совпадает с косой из двух нитей, но при замыкании тоже даёт узел "трилистник"(рис.3).

Два узла эквивалентны тогда и только тогда, когда от диаграммы одного узла к диаграмме другого можно перейти с помощью конечного числа двумерных элементарных операций 1 , 2 , 3 (рис.4).

Можно ли по любой паре диаграмм узнать, эквивалентны узлы или нет, можно ли их распутать?

Оказывается можно, для каждого узла и зацепления можно построить соответствующий ему инвариант. Инварианты позволяют не только различать неодинаковые узлы и отличать узлы от незаузленных петель, но и классифицировать косы. По-разному деформированным вариантам одного и того же узла отвечает один и тот же инвариант; узлы, соответствующие разным инвариантам различны. Но два узла с одним и тем же инвариантом необязательно эквивалентны. Если инвариант узла не равен инварианту тривиального узла, то данный узел не может быть тривиальным и его нельзя распутать. Рассмотрим самые известные инварианты и вычислим их для некоторых зацеплений.

Р L (х) - это многочлен от переменной х с целыми коэффициентами.

Для каждого узла или зацепления L полином Р L (х) существует и однозначно определяется следующими тремя аксиомами.

Эквивалентным диаграммам L и L’ отвечает один и тот же полином: Р L (х)=Р L’ (х).

Тривиальному узлу отвечает полином, равный 1:Р о (х)==1.

Трем зацеплениям L + , L - , L°, которые всюду одинаковы, кроме кружочка, где они выглядят так, как показано на рисунке 5, отвечают полиномы, связанные соотношением

Р L+ (х)-Р L -(х)=х . Р L 0(х).

Для распавшегося зацепления Р L (х) =О.

Вычислим полиномы Конвея для некоторых узлов и зацеплений.

а) Для двух незацепленных окружностей.

L + - диаграмма тривиального узла с одной двойной точкой, L°- диаграмма двух незацепленных окружностей. Из аксиом I и II следует, что Р L +(х) = 1.

Если заменить двойную точку диаграммы L + на противоположную, а затем двойную точку уничтожить (аксиома III), то мы получим диаграмму тривиального узла L - и пару незацепленных окружностей L°.

По аксиоме III, получим Р L +(х)-Р L -(х)=х . Р L 0(х), 1—1=х . Р L 0(х) , Р L 0(х)=0 .

б) Для двух зацепленных окружностей (правое зацепление):

Применяя аксиому III к правой двойной точке, получаем диаграмму L- , эквивалентную паре незацепленных окружностей, и тривиальный узел (с одной двойной точкой) L°.

Используя аксиому I и предыдущий подсчет, получаем Р L -(х)=0 .

Затем по аксиомам I и II получаем Р L 0(х)=1 .

Подставляя эти значения в соотношение аксиомы III, получим Р L +(х)=х. Для левого зацепления полином равен –х

Р L (х)=1,т.к. распутывается в тривиальный узел.
Р L 0 (х) =- х, т.к. распутывается в левое зацепление двух окружностей, значит, Р L (х) = 1 - х 2 по аксиоме 3.

г) Для восьмерки.

Р L (х) = х, так как распутывается в правое зацепление двух окружностей.
Р L (х) = 1, так как распутывается в тривиальный узел.

Поэтому P L’ (x) = 2х по аксиоме 3.

д) Для проколотой восьмерки Р L (х) = х, так как распутывается в правое зацепление двух окружностей.

Пусть зацепление L1 = L 0 .Тогда Р L1 (х)= 1. Р L1 0 (х) = х, так как распутывается в правостороннее зацепление двух окружностей.

Значит, Р L1 (х) = х 2 + 1. В итоге Р L (х) = х 3 + 2х .

Даже небольшое число проведенных вычислений показывает, что полином Конвея — достаточно тонкий инструмент, позволяющий различать узлы и зацепления и устанавливать их нетривиальность. Посчитав, например, полиномы трилистника, восьмерки, и убедившись, что эти полиномы не равны 0 или 1, мы доказали, что их нельзя распутать. Разумеется, эти доказательства верны только в том случае, если уже установлен факт существования и единственности полинома Конвея для каждого узла и зацепления.

Рассмотрим подкласс невозможных фигур, изучаемый теорией кос и узлов.

Определим мультибар как многогранник, состоящий из набора брусков прямоугольного сечения, составляющих фигуру правильного многоугольника. (рис.6).

Опишем каждую сторону многогранника как линию косы и применим к ним основные соотношения теории кос: соотношение далекой коммутативности: ac = ca и соотношение сплетения: aba = bab . (рис 7)

рис.6 рис 7 рис 8 рис.9

Четырехэлементные косы, соответствующие трибару, невозможному квадрату и невозможному пентагону имеют вид: bacbacbac , bacbacbacbac , и bacbacbacbacbac.

Замыкание косы преобразует ее в узел (рис.8, рис.9).

Следовательно, если соединение, соответствующее мультибару, отличается от тривиального четырехэлементного соединения, тогда мультибар является невозможной фигурой.

У теории кос и узлов серьезные приложения к комплексному анализу, механике и физике элементарных частиц, обнаружились глубокие связи между этой теорией и абстрактной алгеброй. Здесь оказались замешаны не только классические разделы физики (статистическая физика, например модель. льда), но и современная квантовая теория. А идея кодирования химической информации в маленьких узелках (и косах!) вновь возникла в молекулярной биологии при расшифровке аминокислот и изучении ДНК.

- раздел топологии и алгебры, изучающий косы и группы, составленные из их классов эквивалентности, и различные обобщения этих групп [1]. Коса из пнитей - объект, состоящий из двух параллельных плоскостей Р 0 и Р 1 в трехмерном пространстве R 3 , содержащих упорядоченные множества точек и из га простых дуг l 1 , . l п , пересекающих каждую параллельную плоскость P t между Р 0 и Р 1 , однократно и соединяющих точки а i > с точками

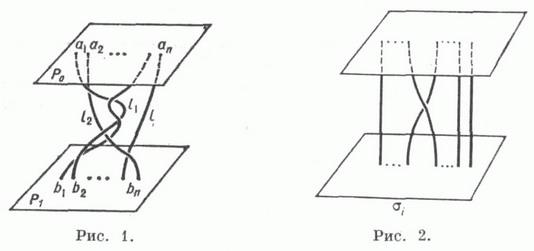
Считается, что а,- лежат на прямой L a в Р й , точки b i - на прямой L b в Р 1 , параллельной L a , причем ft,- расположены под а i для каждого г (см. рис. 1). Косы изображаются в проекции на плоскость, проходящую через эта проекция может быть приведена в общее положение так, что имеется только конечное число двойных точек, попарно лежащих в разных уровнях, и пересечения трансверсальны.

Нить l i косы w соединяет и определяет подстановку Если эта подстановка тождественна, то w наз. крашеной (или чистой) косой. Транспозиции (i i+1) отвечает простейшая коса s i (см. рис. 2).

Во множестве всех кос с пнитями и с фиксированными P 0 . P 1 , , (b i > вводится отношение эквивалентности. Оно определяется гомеоморфизмами где П - область между Р 0 и P 1 , тождественными на к-рые можно считать такими, что h(P t )=P t . Косы а и Р эквивалентны, если существует такой гомеоморфизм hи

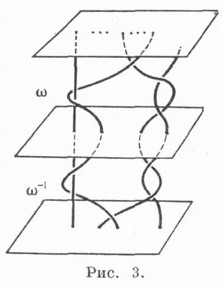
Классы эквивалентности, далее также называемые косами, образуют группу кос В(п).относительно операции, определяемой следующим образом. Экземпляр П' области П помещается над другим экземпляром П" так, чтобы совпала с а затем сжимается вдвое. Образы кос дают косу нить l i к-рой получается продолжением l i с помощью Единичная коса - класс эквивалентности, содержащий косу из n параллельных отрезков, коса w -1 , обратная косе w, определяется отражением в плоскости Р 1/2 . Условие - на рис. 3. Отображение определяет эпиморфизм В(п).на группу S(п).перестановок пэлементов, ядром к-рого является подгруппа К(п), соответствующая всем чистым косам, так что имеется точная последовательность

Группа кос В(п).имеет две основные интерпретации. Первая - пространство конфигурации - получается отождествлением плоскостей Р t с помощью вертикальной проекции на Р 0 , при к-рой образы точек при изменении tот 0 до 1 образуют след изотопии множества по причем Косе однозначно соответствует класс гомотопных петель в пространстве неупорядоченных наборов G(n).из ппопарно различных точек плоскости, и имеет место изоморфизм

Для крашеных кос аналогично строится изоморфизм

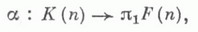
где F(п) - пространство упорядоченных наборов из га различных точек плоскости, так что К(п).можно отождествить с подгруппой, отвечающей накрытию

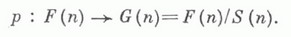
Вторая - группа гомеотопий - получается продолжениями изотонии до изотопии плоскости Р 0 тождественной вне нек-рого диска, причем При каждом tдва такие продолжения отличаются на гомеоморфизм, тождественный в точках а it . Косе однозначно соответствует компонента пространства гомеоморфизмов Y(п).плоскости, отображающих множество на себя, и имеет место изоморфизм

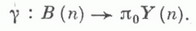
Каждому гомеоморфизму сопоставляется автоморфизм свободной группы ранга , определенный с точностью до внутреннего, к-рый в свою очередь дает гомоморфизм Элементы образа наз. Носовыми автоморфизмами свободной группы. В частности, косе s i отвечает автоморфизм

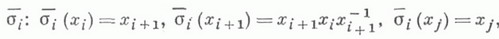
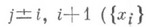
если - базис F n ). Любой носовой автоморфизм а обладает свойствами:

с точностью до внутреннего (смысл А i - ниже), эти свойства характеризуют косовые автоморфизмы. Косы являются образующими группы В (п), т. е. причем

Оказывается, что (1) - копредставление для В(п).(см. рис. 4). Имеет место расщепляющая точная последова-

тельность (получающаяся из локально тривиального расслоения со слоем

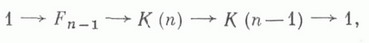
к-рая приводит к нормальному ряду

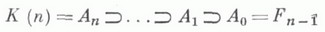
со свободными факторами причем А i имеет "дополнение" U n-i , изоморфное К( п-i-1). Каждый элемент может быть представлен единственным образом в виде где p w - выбранный представитель для в В(п), а Приведение косы к такой форме наз. ее причесыванием. Это решает проблему тождества в В(п).

Копредставление для К(п).таково: образующие (см. рис. 5)

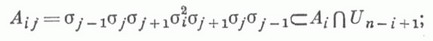
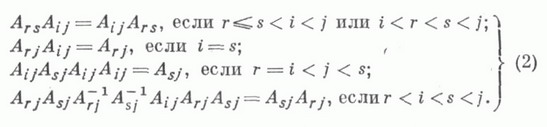
Оно может быть получено как копредставление ядра естественного гомоморфизма в S(п).абстрактной группы В (n), заданной копредставлением (1) с помощью Шрей ера системы

Центр группы B(п) - бесконечная циклич. группа, порожденная элементом Коммутант В' (п).совпадает с В" (п).при В'(3) изоморфна свободной группе ранга 2, а В'(4) -полупрямому произведению двух таких групп. Фактор по коммутанту - бесконечная циклич. группа, порожденная образами s i . Элементы конечного порядка в В(га) отсутствуют. Группа К(п).переходит в себя при эндоморфизмах с неабелевым образом. В частности, - вполне характе-ристич. подгруппа в В(n). а также и в К(п).(см. [15]).

Проблема сопряженности в В(n) решается существенно сложнее проблемы тождества. Имеется единственная нормальная по Гарсайду форма косы где - так наз. элемент Гарсайда, W - положительная, т. е. имеющая запись через s i с положительными показателями, коса. Косе w конечным числом операций, определяемых по i(сопряжение с нек-рыми элементами, выбор элементов максимальной степени и т. п.), сопоставляется нек-рое множество слов из к-рого выбирается слово в нормальной форме с минимальным Т. Это - так наз. верхняя форма косы w. Оказывается, что две косы сопряжены тогда и только тогда, когда их верхние формы совпадают (см. [7]). Представление Бурау группы кос В(п).в группу матриц над кольцом целочисленных многочленов одной переменной определяется соответствием:

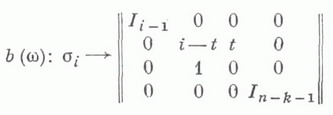
где I k - единичная матрица порядка k. Матрица есть приведенная матрица Александера (см. Александера инварианты).зацепления, полученного замыканием косы w (см. ниже). Для крашеной косы из аналогичной матрицы Гаснера получается полная матрица Александера. Проблема точности этих представлений не решена (1982) (см. [2]).

То, что пространства F(п).и G(n).асферичны, дает возможность вычислить гомологии групп кос.

Гомологии К(п).(см. [16]): гомологически К(п).совпадает с произведением букетов окружностей, в к-рых число окружностей увеличивается от одной до n-1. Кольцо когомологий изоморфно внешнему градуированному кольцу, порожденному одномерными элементами с соотношениями В качестве w rl можно взять формы

отвечающие обходу диагоналей Гомологии В(п).(см. [8], [12]): гомоморфизм может быть продолжен вложением ; индуцированный гомоморфизм в когомологиях эпиморфен, т. е. когомологии mod 2 группы В(п).порождаются классами Штифеля- Уитни.

Имеется естественное отображение G(n) в - пространство сфероидов (вокруг и точек берутся малые диски, к-рые канонически со степенью I отображаются в сферу, а все дополнение - в точку). Это отображение (см. [14]) устанавливает гомологич. эквивалентность предельного пространства (индекс означает, что берется компонента сфероидов степени 0). Относительно нестабильных групп гомологии В(п).доказано [16], что они конечны, стабилизируются с ростом и и имеется правило повторения Дано [17] описание вычисления этих групп.

Приложения и обобщения. 1) Замкнутой косой наз. зацепление (n-компонентный узел).в R 3 , каждая компонента к-рого трансверсально пересекает полуплоскости, ограниченные одной и той же прямой - осью Iзамкнутой косы (см. рис. 6). Коса порождает замкнутую косу (замыкание w) следующим образом. Цилиндр с основаниями на P 0 и P 1 , содержащий внутри себя w, изгибается в R 3 так, что образующие переходят в окружности с центрами на прямой l, а основания совмещаются и каждая точка а i , совпадает с b i . Тогда объединение нитей l i перейдет в Обратно, каждое зацепление в R 3 может быть представлено замкнутой косой. Эквивалентным косам отвечают изотопные зацепления и, более того, сопряженные косы дают изотопные зацепления. Обратное неверно, так как зацепление может быть представлено косами с разным числом нитей. Кроме того, косы не сопряжены в В(п), но отвечают изотопным зацеплениям. Если две замкнутые косы эквивалентны как зацепления, то они могут быть получены одна из другой цепочкой элементарных преобразований двух типов (см. рис. 7). Эти операции интерпретируются в терминах копредставлений группы зацеплений, что дает алгебраич. переформулировку проблемы изотопности зацеплений в виде вопроса о системе групп В(п). Копредставление группы зацепления имеет вид

где соотношения определены косовым автоморфизмом b w . Обратно, каждое такое соотношение определяет косу.

2) Если разрезать поверхность рода gспомощью gнепересекающихся сечений так, что получится сфера с 2g дырами, то гомеоморфизмы этой сферы с дырами, оставляющие на месте точки на краях дыр, определяют гомеоморфизмы поверхности, неподвижные на сечениях, и сами определяются с точностью до изотонии элементами группы K(2g). Это дает представление группы кос в группе гомеотопий поверхности. Аналогично строится и представление В(2g). Эти представления используются при изучении диаграмм Хегора трехмерных многообразий.

3) Отождествлением R 2 с комплексной прямой С 1 и сопоставлением неупорядоченному набору из " точек плоскости многочлена степени п, имеющего эти точки своими корнями, получается возможность отождествить

G(n).с пространством многочленов с ненулевым дискриминантом. Так, этот факт позволил получить ряд результатов о непредставимости алгебраич. функций суперпозицией функций от меньшего числа переменных (см. [16]).

4) Пространства конфигураций для любого пространства Xопределяются аналогично G(п).и F(п).с заменой R 2 на X. Фундаментальные группы этих пространств В(X).и К(X).наз. группами кос пространства Xи чистых кос соответственно. Для многообразия М n размерности больше , и эти группы интереса не представляют. Для двумерного многообразия имеется естественное вложение В(п).и К(п).в В n ( М 2 ).и К п ( М 2 ), индуцированное вложением Для М 2 , отличного от сферы и проективной плоскости, получается точная последовательность

для сферы гомоморфизм еявляется эпиморфизмом, полученным добавлением к (1) еще одного соотношения

5) Если есть fc-листное накрытие, то где а - петля в Y, является петлей в пространстве конфигураций X, чем определяется гомоморфизм к-рый усиливает монодромию накрытия и находит применение в алгебраич. геометрии.

6) Пусть - комплексификация действительного векторного пространства V,a W - конечная неприводимая группа, порожденная отражениями, действующая в V (и, следовательно, в ). Пусть s i - порождающие отражения в плоскостях и D - их объединение.

Пусть, наконец, - факторпространство. Группы наз. группами Брискорна, они естественно обобщают К(п).и В(п). Если , то имеет копредставление вида где число сомножителей с каждой стороны равно т/у (а/ здесь соответствует камере Вейля). Для этих групп доказано, что X W и Y W являются пространствами типа К ( п,1), решена проблема сопряженности. В алгебраич. геометрии пространства Х^г появляются как дополнения к дискриминанту версальных деформаций рациональных особенностей (см. [12],[13]).

Лит.:[1 ] А r t f п Е., "Ann. Math.", 1947, V. 48, p. 101-26, 643-49; [2] Birman J., "Ann. Math. St.", 1974, №82; [3] Burau W., "Hamburg- Abh.", 1932, Bd 9, S. 117-24; [4] Марков А. А., "Тр. Матем. ин-та АН СССР", 1945, т. 16; [5] Gassner В., "Hamburg Abh.", 1961, Bd 25, S. 10-22; [6] F a d e 1 1 E., N e u w i r t h L., "Math. Scand.", 1962, v. 10, p. 111 - 18; 17] Г а р с а и д Ф., "Математика", 1970, т. 14, № 4, с. 116-32; [8] Ф у к с Д. Б., "Функциональный анализ и его приложения", 1970, т. 4, №2, с. 62-73; [9] Арнольд В. И., там же, № 1, с. 84-85; [10] Г о р и н Е. А.. Л и н В. Я., "Матем. сб.", 1969, т. 78, с. 579-610; [11] А р н о л ь д В. И., "Тр. Моск. матем. об-ва", 1970, т. 21, с. 27-46; [12] Брискорн Э., "Математика", 1974, т. 18, №3, с. 46-59; ИЗ] Брискорн Э., Сайто К., там же, М 6, с. 56-79; S14] D е 1 i g п е P., "Invent. Math.", 1972, v. 17, № 4, p. 273-302; [15] Л и н В. Я., "Успехи матем. наук", 1974, т. 29, в. 1, с. 173-74; [16] Арнольд В. И., "Матем. заметки", 1969, т. 5, № 2, с. 227-31; [17] Л и н В. Я., в кн.: Итоги науки и техники. Алгебра. Топология. Геометрия, т. 17, М., 1979, с. 159-227. А. В. Чернавский.

Математическая энциклопедия. — М.: Советская энциклопедия . И. М. Виноградов . 1977—1985 .

Читайте также: