Теорема ферма доказательство кратко

Обновлено: 04.07.2024

уравнение не имеет решений при любых целых ненулевых числах a, b и c, если n-целое число больше двух (n > 2).

Ваша теория, что бозон Хиггса это чёрная дыра, которая ускоряется в обратную сторону сквозь время, бесподобна… Жаль только, что она не верна… - Как не верна?! Этого просто не может быть. – Вы сделали арифметическую ошибку на странице два, причём абсолютно глупую…

В конечном счёте, были найдены доказательства для всех значений n примерно до 4 миллионов, сначала вручную, а затем при помощи компьютера. Однако, не было найдено общего доказательства, которое было бы справедливым для всех возможных значений n, а также ни единого намёка на то, что такое доказательство может существовать в принципе.

Примерно в это же время, английский математик Эндрю Джон Уайлс (Andrew John Wiles) понял, что близок к решению задачи и решил уединиться для продолжения работы. Уайлс доказывал теорему в тесном семейном кругу с женой и тремя детьми, запершись на уютной даче на семь лет, с 1986 по 1993 г.г. Это представляется ещё более выдающимся подвигом, если вы вспомните на даче себя и всё это длится семь лет – кошмар, от которого невозможно проснуться.

В 1993 г. Эндрю Уайлс уже был совершенно уверен, что Великая теорема Ферма доказана. Однако, он объявил об этом не напрямую, а запросил три лекции на математической конференции в Кембридже. Причём, в заявленной теме выступления не было никакого намёка на теорему Ферма. Уайлс считался довольно серьёзным математиком, поэтому его лекции были восприняты всеми как приятный бонус, дополнительное украшение конгресса.

Тем не менее, Уайлс нашёл в себе силы и волю для продолжения борьбы. Он пригласил аспиранта Ричарда Тейлора и уже вдвоём они довели доказательство теоремы Ферма до ума. К концу 1994 г. всё было завершено.

Как писал сам Уайлс:

…утром 19 сентября 1994 г. я был на грани того, чтобы сдаться и почти смирился с тем, что потерпел неудачу…Я сидел за столом …и внезапно на меня снизошло невероятное откровение…Казалось возник истинный ответ на проблему. Это было неописуемо красиво; это было так просто и элегантно. Я не мог понять, как пропустил это и просто сидел и смотрел на расчёты в недоумении минут двадцать. Затем в течение дня я ходил и, то и дело, возвращался к столу, чтобы посмотреть, там ли они ещё. Расчёты всё ещё были там…Это был самый важный момент в моей жизни…

Говорят, на сегодняшний день в мире существует не более 1000 человек способных понять доказательство Эндрю Уайлса. Простота формулировки теоремы и, в то же время, невероятная сложность единственного известного доказательства, вдохновляют неофитов на попытки найти другое, более простое решение задачи. При этом предполагается, что оно является настолько очевидным, что вполне разрешимо на уровне знаний XVII века. Что же касается практического применения теоремы, то оно и по сей день остаётся неизвестным.

Спасибо, что дочитали до конца. Ставьте "лайки" и оставайтесь на связи. Подписывайтесь на канал "ТыжИсторик", будет ещё много интересного.

Не много идей и рассуждений занимали мысли и внимание ученых-математиков и самоучек так долго, как Великая теорема Ферма. Эта теорема – самое известное математическое утверждение, на доказательство которого понадобилось больше 380 лет. Более того, в 1908 году ажиотаж вокруг нее был накален после обещания присудить премию за ее решение.

Вся сложность доказательства этой теоремы состояла в том, что нужно было доказать отсутствие решения. Казалось, что ее суть так легко понять, но как тяжело было ее решить!

Доказательство этой единой математической теоремы тесно связано с развитием истории математики, формированием новых направлений и углублением человеческого знания об абстракциях. О том, кто доказал теорему Ферма и сколько времени на это ушло, мы поговорим в этой статье.

Наибольший научный вклад Ферма в развитие математики в том, что он обратил внимание на роль, которую занимают простые числа.

Великая теорема Ферма

Рассуждения Ферма о натуральных числах были не единственными, и даже не Пифагор первым их обосновал. История исчислений натуральных чисел была известна еще в Шумере и Древней Индии, но только Пифагор записал эти рассуждения в современной математической формуле: x 2 + y 2 = z 2 , а Ферма увеличил количество неизвестных: x n + y n = z n .

Доказать выдвинутое утверждение Ферма, что нет простого решения для уравнения, например, 3 2 +4 2 =5 2 , когда n˃2, являющегося целым числом, впоследствии смогли немногие. Сегодня известно, что Ферма доказал отсутствие решения для n = 4. А из его переписки известно, что он также осуществил и доказательство для n = 3, но найти его среди писем не удалось.

Малая теорема Ферма – это еще одно знаменитое рассуждение, которое Ферма описал в письме к своему другу в 1640 году. Читается эта теорема так: если целое число п не делится на простое число р, то п р — 1 —1 делится на число р.

Доказательство этой теоремы не заняло столько времени и усилий, как в случае с ее предшественницей, но ее роль в развитии математического мышления несомненно бесценна. Сегодня она является одной из самых важных теорем элементарной теории чисел, криптографии и современной алгебры.

Великая теорема Ферма: доказательство

Великая теорема Ферма не была детально объяснена даже самым автором. Может быть, его бумаги затерялись, но, скорее всего, в этом он сам не видел необходимости.

Другим предположением, почему Ферма не развил детальное объяснение своей теоремы, в том, что он не был профессиональным математиком, как, к примеру, Рене Декарт или Франсуа Виет, и тем более он не пытался достичь признания в этой сфере, помимо одобрения друзей и единомышленников, которое, очевидно, уже получил. Но, тем не менее, Ферма понимал оригинальность своих идеи и подходов, а также то, что его методы мышления помогают другим математикам.

Увлекаясь теорией простых чисел, Ферма понимал, что натуральные числа не являются бесконечными. Он полагал, что найденный им метод является общим, и его можно будет использовать, чтобы доказать любые теоремы натуральных чисел. Но реальность оказалась иной. Метод оказался не таким универсальным, как рассуждал Ферма. И на доказательство этого ученым понадобилось более трех столетий.

В начале 1990-х годов теорему Ферма уже доказали для показателей разных степеней вплоть до 4 000 000. Но все-таки ученые продолжали искать показатель, для которого теорема окажется ложной.

Математик из Принстонского университета Эндрю Уайлс смог доказать теорему в 1993 году, исполнив свою мечту, которая появилась у него в 10-летнем возрасте. На протяжении долгих лет он следил за многочисленными методами, с помощью которых разные ученые пытались доказать теорему Ферма. И в 1986 году, оставив все свои проекты, он сам занялся доказательством этой теории, которое заняло 7 лет.

В своем доказательстве он использовал сложные методы вычисления. Его работа опиралась на труды гигантов из разных направлений математики. Теорема Ферма – это сложная головоломка, решить которую стало возможным, сочетая поэтапно разные подходы и методы доказательства. Исписывая тысячи страниц, Уайлс смог доказать Великую теорему Ферма.

Это был долгий путь, который заключался в подсчете бесконечностей, рассмотрении всех ранее использованных подходов с целью найти собственный метод доказательства. Сначала Уайлс подсчитал все эллиптические функции, а также модулярные эллиптические функции, где как одних, так и других бесконечно много, чтобы показать, что их вычисления эквивалентны. Хотя этот подход оказался неэффективным, он помог осознать, куда двигаться дальше. Эти вычисления помогли Уайлсу понять, что нужно вместо доказательства гипотезы Таниямы-Симуры для эллиптических кривых, доказать эту же гипотезу лишь для полустабильных кривых.

Далее он обратился к теории Галуа, и с ее помощью смог определить эллиптические уравнения и доказать, что можно провести ассоциацию с элементами модулярных форм. Так Уайлсу удалось переформулировать задачу в более податливые понятия. Но это был только первый шаг, который занял два года.

Позднее он пробовал решить теорему с помощью теории Ивасавы, но ее оказалось недостаточно, поэтому Уайлс использовал еще и инструменты системы Эйлера. Однако позже он понял, что самым подходящим подходом является подход Колывагина-Флаха. И здесь новая тактика начала приносить плоды.

Окончательные результаты и первое публичное доказательство Уайлс представил на конференции в Кембридже в июне 1993 года. Для этого эму понадобилось три часа. Рукопись занимала 200 страниц. Потом решение задачи подтвердил комитет экспертов, и, после уточнения нескольких неточностей, в 1995 году теорема Ферма официально была доказана.

Вклад Пьера Ферма в развитие науки

История математики просто немыслима без вклада ученого-самоучки Пьера Ферма. Но из-за уединенного образа жизни и узкого круга общения его идеи ученые смогли оценить лишь после его смерти и благодаря его сыну Сэмюелю, который в 1870 году начал публиковать наброски и размышления отца.

Ферма и его идеи во многом стали основополагающими для развития новых математических теорий. Его сильной стороной был творческий подход и неограниченность рамками одной дисциплины: Ферма применял алгебраические методы в геометрических задачах, что заложило основания аналитической геометрии. Поэтому справедливо считать, что Ферма, наравне с Декартом, повлиял на формирование аналитической геометрии, а также то, что в своей переписке с Паскалем он заложил основы теории вероятности.

Судя по популярности запроса "теорема Ферма - краткое доказательство", эта математическая проблема действительно многих интересует. Эта теорема была впервые высказана Пьером де Ферма в 1637 году на краю копии "Арифметики", где он утверждал, что у него было ее решение, оно было слишком велико для того, чтобы поместиться на краю.

Историческая справка

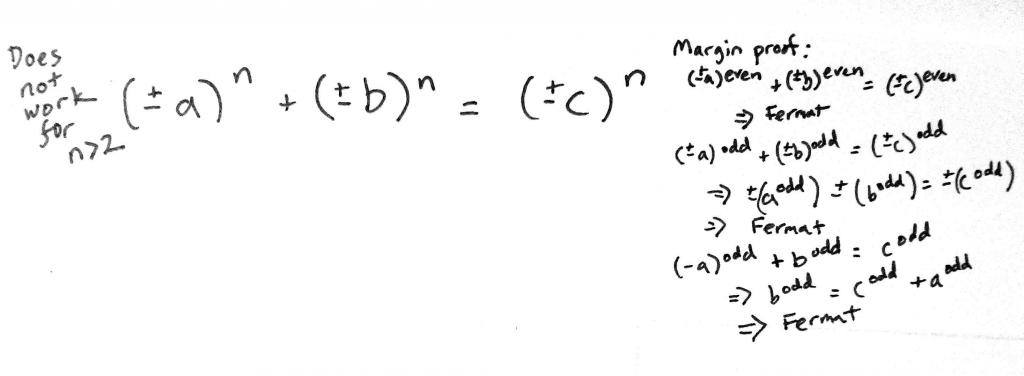
Теорема в конечном итоге стала одной из самых заметных нерешенных проблем математики. Попытки доказать это вызвали существенное развитие теории чисел, и с течением времени последняя теорема Ферма получила известность как нерешенная проблема математики.

Краткая история доказательств

Если n = 4, что доказано самим Ферма, достаточно доказать теорему для индексов n, которые являются простыми числами. В течение следующих двух столетий (1637-1839) гипотеза была доказана только для простых чисел 3, 5 и 7, хотя Софи Жермен обновляла и доказывала подход, который имел отношение ко всему классу простых чисел. В середине 19 века Эрнст Куммер расширил это и доказал теорему для всех правильных простых чисел, в результате чего нерегулярные простые числа анализировались индивидуально. Основываясь на работе Куммера и, используя сложные компьютерные исследования, другие математики смогли расширить решение теоремы, имея цель охватить все основные показатели до четырех миллионов, но док-во для всех экспонентов по-прежнему было недоступным (это означает, что математики обычно считали решение теоремы невозможным, чрезвычайно сложным, или недостижимым с современными знаниями).

Работа Шимуры и Таниямы

В 1955 году японские математики Горо Шимура и Ютака Танияма подозревали, что существует связь между эллиптическими кривыми и модульными формами, двумя совершенно разными областями математики. Известная в то время, как гипотеза Танияма-Шимура-Вейля и (в конечном счете) как теорема модульности, она существовала сама по себе, без видимой связи с последней теоремой Ферма. Она сама по себе широко рассматривалась как важная математическая теорема, но при этом считалась (как и теорема Ферма) невозможной для доказательства. В то же время доказательство великой теоремы Ферма (методом деления и применения сложных математических формул) было осуществлено лишь полвека спустя.

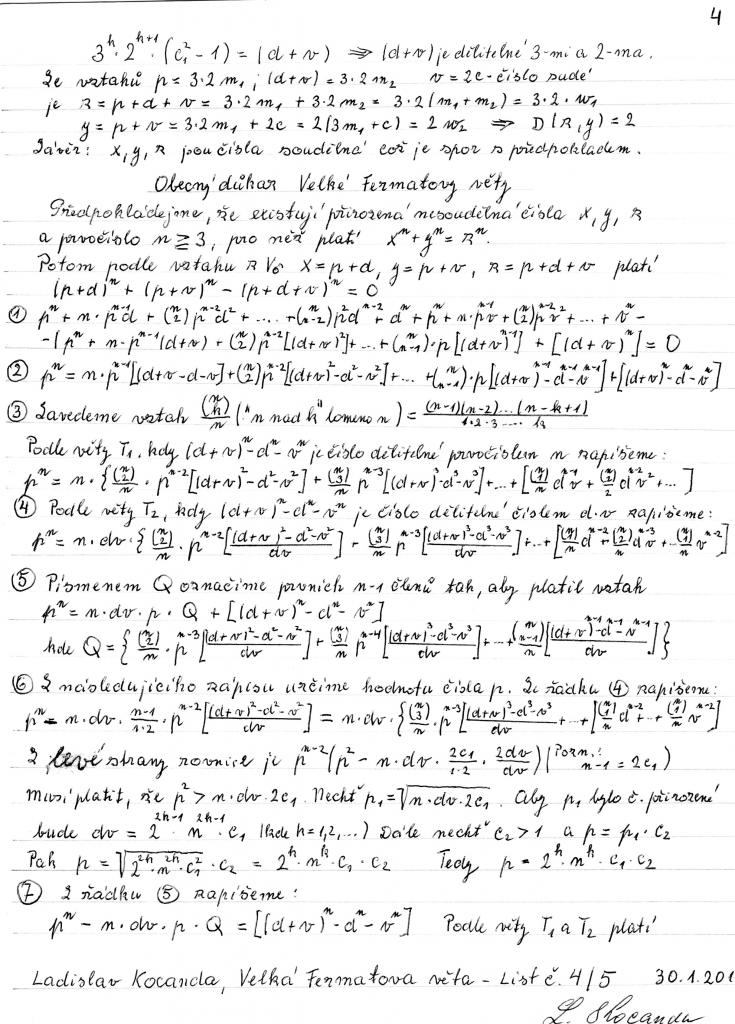
Хотя обе теоремы были сложными проблемами для математики, считающимися нерешаемыми, работа двух японцев стала первым предположением о том, как последняя теорема Ферма могла бы быть продолжена и доказана для всех чисел, а не только для некоторых. Важным для исследователей, выбравших тему исследования, был тот факт, что в отличие от последней теоремы Ферма, теорема модульности была основной активной областью исследований, для которой было разработано доказательство, а не только исторической странностью, поэтому время, затраченное на ее работу, могло быть оправдано с профессиональной точки зрения. Однако общее мнение заключалось в том, что решение гипотезы Таниямы-Шимуры оказалось нецелесообразным.

Великая теорема Ферма: доказательство Уайлса

Узнав, что Рибет доказал правильность теории Фрея, английский математик Эндрю Уайлс, с детства интересующийся последней теоремой Ферма и имеющий опыт работы с эллиптическими кривыми и смежными областями, решил попытаться доказать гипотезу Таниямы-Шимуры, как способ доказать последнюю теорему Ферма. В 1993 году, спустя шесть лет после объявления о своей цели, тайно работая над проблемой решения теоремы, Уайльсу удалось доказать смежную гипотезу, что, в свою очередь, помогло бы ему доказать последнюю теорему Ферма. Документ Уайлса был огромным по размеру и масштабу.

Недостаток был обнаружен в одной части его оригинальной статьи во время рецензирования и потребовал еще один год сотрудничества с Ричардом Тейлором, чтобы совместно решить теорему. В результате окончательное доказательство Уайлсом великой теоремы Ферма не заставило долго себя ждать. В 1995 году оно было опубликовано в куда меньшем масштабе, чем предыдущая математическая работа Уайлса, наглядно показывая, он не ошибся в своих предыдущих выводах о возможности доказательства теоремы. Достижение Уайлса было широко растиражировано в популярной прессе и популяризировано в книгах и телевизионных программах. Остальные части гипотезы Танияма-Шимура-Вейля, которые теперь были доказаны и известны как теорема о модульности, впоследствии были доказаны другими математиками, которые основывались на работе Уайлса в период между 1996 и 2001 годами. За свое достижение Уайлс был удостоен чести и получил многочисленные награды, в том числе, премию Абеля 2016 года.

Доказательство Уайлсом последней теоремы Ферма является частным случаем решения теоремы модульности для эллиптических кривых. Тем не менее, это самый известный случай столь масштабной математической операции. Вместе с решением теоремы Рибе, британский математик также получил доказательство последней теоремы Ферма. Последняя теорема Ферма и теорема о модульности почти повсеместно считались недоказуемыми современными математиками, но Эндрю Уайлс смог доказать всему научному миру, что даже ученые мужи способны заблуждаться.

Характеристика работы

Доказательство теоремы Ферма Эндрю Уайлсом использует многие методы из алгебраической геометрии и теории чисел и имеет много разветвлений в этих областях математики. Он также использует стандартные конструкции современной алгебраической геометрии, такие как категория схем и теория Ивасавы, а также другие методы XX века, которые не были доступны Пьеру Ферма.

Как это было

Одним из людей, анализировавших первоначальную рукопись Уайлса с решением теоремы, был Ник Кац. В ходе своего обзора он задал британцу ряд уточняющих вопросов, которые заставили Уайлса признать, что его работа явно содержит пробел. В одной критической части доказательства была допущена ошибка, которая давала оценку для порядка конкретной группы: система Эйлера, используемая для расширения метода Колывагина и Флача, была неполной. Ошибка, однако, не сделала его работу бесполезной - каждая часть работы Уайлса была очень значительной и новаторской сама по себе, как и многие разработки и методы, которые он создал в ходе своей работы и которые затрагивали лишь одну часть рукописи. Тем не менее в этой первоначальной работе, опубликованной в 1993 году, действительно не было доказательства великой теоремы Ферма.

Уайлс заявляет, что утром 19 сентября 1994 года он был на грани того, чтобы бросить все и сдаться, и почти смирился с тем, что потерпел неудачу. Он готов был опубликовать свою неоконченную работу, чтобы другие могли на ней основываться и найти, в чем он ошибся. Английский математик решил дать себе последний шанс и в последний раз проанализировал теорему, чтобы попытаться понять основные причины, по которым его подход не работал, как вдруг внезапно осознал, что подход Колывагина-Флака не будет работать, пока он не подключит к процессу доказательства еще и теорию Ивасавы, заставив ее работать.

История великой проблемы

Решение этой теоремы считалось самой большой проблемой в математике на протяжении многих столетий. В 1816 и в 1850 годах Французская академия наук предложила приз за общее доказательство великой теоремы Ферма. В 1857 году Академия присудила 3000 франков и золотую медаль Куммеру за исследования идеальных чисел, хотя он и не подавал заявку на приз. Еще одна премия была предложена ему в 1883 году Брюссельской академией.

Премия Вольфскеля

Лавры Ферма достались японцам

Как уже говорилось ранее, примерно в 1955 году японские математики Горо Шимура и Ютака Танияма открыли возможную связь между двумя, по-видимому, совершенно разными отраслями математики - эллиптическими кривыми и модульными формами. Полученная в результате их исследований теорема модульности (в то время известная как гипотеза Таниямы-Шимуры) гласит, что каждая эллиптическая кривая является модулярной, что означает, что она может быть связана с уникальной модулярной формой.

Теория первоначально была отклонена как маловероятная или весьма спекулятивная, но была воспринята более серьезно, когда теоретик чисел Андре Вейль нашел доказательства, подтверждающие выводы японцев. В результате гипотеза часто называлась гипотезой Таниямы-Шимуры-Вейля. Она стала частью программы Langlands, представляющей собой список важных гипотез, требующих доказательства в будущем.

Даже после серьезного внимания, гипотеза была признана современными математиками как чрезвычайно трудная или, возможно, недоступная для доказательства. Теперь именно эта теорема ждет своего Эндрю Уайлса, который смог бы удивить весь мир ее решением.

Теорема Ферма: доказательство Перельмана

Не смотря на расхожий миф, российский математик Григорий Перельман, при всей своей гениальности, не имеет никакого отношения к теореме Ферма. Что, впрочем, никак не умаляет его многочисленных заслуг перед научным сообществом.

Вели́кая теоре́ма Ферма́ (или последняя теорема Ферма) — одна из самых популярных теорем математики; её условие формулируется на понятийном уровне среднего общего образования, а доказательство теоремы искали многие математики более трёхсот лет. Окончательно доказана в 1995 году Уайлсом.

Содержание

Формулировка

Теорема утверждает, что:

$a^n+b^n=c^n\,\!$

Для любого натурального n > 2 уравнение

не имеет натуральных решений a , b и c .

История

Для случая n = 3 эту теорему в X веке пытался доказать среднеазиатский математик ал-Ходжанди, но его доказательство не сохранилось.

Наоборот, невозможно разложить куб на два куба, биквадрат на два биквадрата и вообще никакую степень, большую квадрата, на две степени с тем же показателем. Я нашел этому поистине чудесное доказательство, но поля книги слишком узки для него.

Cubum autem in duos cubos, aut quadrato-quadratum in duos quadrato-quadratos, et generaliter nullam in infinitum ultra quadratum potestatem in duas ejusdem nominis fas est dividere; cujus rei demonstrationem mirabilem sane detexi. Hanc marginis exiguitas non caperet.

Несколько позже сам Ферма опубликовал доказательство частного случая для n = 4 , что добавляет сомнений в том, что у него было доказательство общего случая, иначе он непременно упомянул бы о нём в этой статье.

Эйлер в 1770 доказал теорему для случая n = 3 , [1] Дирихле и Лежандр в 1825 — для n = 5 , Ламе — для n = 7 . Куммер показал, что теорема верна для всех простых n, меньших 100, за возможным исключением 37, 59, 67.

Над полным доказательством Великой теоремы работало немало выдающихся математиков, и эти усилия привели к получению многих результатов современной теории чисел. Считается, что теорема стоит на первом месте по количеству неверных доказательств.

В 1908 году немецкий любитель математики Вольфскель завещал 100000 марок тому, кто докажет теорему Ферма. После Первой мировой войны премия обесценилась.

В 1980-х годах появился новый подход к решению проблемы. Из гипотезы Морделла, доказанной Фальтингсом в 1983 году, следует, что уравнение a n + b n = c n при n > 3 может иметь лишь конечное число взаимно простых решений.

Первый вариант своего доказательства Уайлс опубликовал в 1993 году (после 7 лет напряжённой работы), но в нём вскоре обнаружился серьёзный пробел; с помощью Ричарда Лоуренса Тейлора пробел удалось достаточно быстро ликвидировать. [4] В 1995 году был опубликован завершающий вариант. [5]

Теорема Ферма в культуре и искусстве

См. также

Примечания

Литература

На русском

На английском

Faltings, Gerd (1995). The Proof of Fermat’s last theorem by R. Taylor and A. Wiles, Notices of the AMS (42) (7), 743—746.
Daney, Charles (2003). The Mathematics of Fermat’s last theorem. Retrieved Aug. 5, 2004.
O’Connor, J. J. & and Robertson, E. F. (1996). Fermat’s last theorem. The history of the problem. Retrieved Aug. 5, 2004.
Shay, David (2003). Fermat’s last theorem. The story, the history and the mystery. Retrieved Aug. 5, 2004.
The Moment of Proof : Mathematical Epophanies, by Donald C. Benson; Oxford University Press; ISBN 0-19-513919-4 (paperback, 1999)

Wikimedia Foundation . 2010 .

Полезное

Смотреть что такое "Ферма великая теорема" в других словарях:

Ферма великая теорема — утверждение П. Ферма о том, что диофантово уравнение (См. Диофантовы уравнения) xn + yn = zn, где n – целое число, большее двух, не имеет решений в целых положительных числах. Ф. в. т. установлена для ряда частных значений n, однако… … Большая советская энциклопедия

Ферма малая теорема — Малая теорема Ферма классическая теорема теории чисел, которая утверждает что Если p простое число и целое a не делится на p, то a p 1 ≡ 1 (mod p) (или a p 1 1 делится на p). Иная формулировка: Для любого простого … Википедия

Ферма Пьер — Ферма (Fermat) Пьер (17.8.1601, Бомон де Ломань, √ 12.1.1665, Кастр), французский математик. По профессии юрист: с 1631 был советником парламента в Тулузе. Автор ряда выдающихся работ, большинство из которых было издано после смерти Ф. его сыном … Большая советская энциклопедия

Теорема Ферма — Теоремы Ферма были сформулированы Пьером Ферма: Великая теорема Ферма Малая теорема Ферма Лемма Ферма о локальном экстремуме … Википедия

Ферма — I Ферма (Fermat) Пьер (17.8.1601, Бомон де Ломань, – 12.1.1665, Кастр), французский математик. По профессии юрист: с 1631 был советником парламента в Тулузе. Автор ряда выдающихся работ, большинство из которых было издано после смерти Ф.… … Большая советская энциклопедия

ФЕРМА ТЕОРЕМА — великая теорема Ферма, знаменитая теорема Ферма, большая теорема Ферма, последняя теорема Ферма, утверждение, что для любого натурального числа п>2 уравнение xn+yn=zn (уравнение Ферма) не имеет решений в целых ненулевых числах х, у, z. Она была… … Математическая энциклопедия

ФЕРМА — • ФЕРМА (Fermat) Пьер де (1601 65), французский математик. Вместе с Блезом ПАСКАЛЕМ сформулировал теорию вероятности и, доказав, что свет перемещается по самой короткой оптической траектории (принцип Ферма), стал основателем геометрической оптики … Научно-технический энциклопедический словарь

ТЕОРЕМА — ТЕОРЕМА, утверждение или предложение, которое доказывается логическими рассуждениями, основанными на фактах и АКСИОМАХ. см. также ВЕЛИКАЯ ТЕОРЕМА ФЕРМА … Научно-технический энциклопедический словарь

Читайте также: