Сформулируйте теорему об окружности вписанной в правильный многоугольник кратко

Обновлено: 05.07.2024

Конспект
Правильным многоугольником называется выпуклый многоугольник, у которого все углы равны и все стороны равны.
Зная, что сумма всех углов такого n-угольника равна полупроизведению числа сторон на 180 градусов, можно получить формулу для вычисления угла α_n правильного n-угольника, разделив общую сумму на число равных между собой углов: α_n = (n - 2)/n ∙ 180°
Докажем теорему об окружности, описанной около правильного многоугольника.
Около любого правильного многоугольника можно описать окружность, и притом только одну.

Пусть A₁ A₂ A₃ … A_n – правильный многоугольник, О – точка пересечения биссектрис углов A₃ и A₂.
Докажем, что отрезок OA₁ равен OA₂ равен OA₃ и так далее равен OA_n. Так как многоугольник правильный, то угол A₂ равен углу A₃, а значит, угол 1 равен углу 3. Отсюда следует, что треугольник OA₂ A₃ равнобедренный, и, следовательно, равны отрезки OA₃ и OA₂.
Треугольники OA₂ A₃ и треугольник OA₂ A₁ равны по двум сторонам и углу между ними (A₂ A₃ = A₁ A₃, A₂ O – общая сторона и угол 3 равен углу 4, следовательно, OA₃ = OA₁.
Аналогично можно доказать, что OA₄ = OA₂, OA₅ = OA₃ и так далее. Таким образом, доказали, что точка О равноудалена от всех вершин многоугольника, поэтому окружность с центром в точке О и радиусом OA₁ является описанной около многоугольника.
Докажем теорему об окружности, вписанной в правильный многоугольник.
В любой правильный многоугольник можно вписать окружность, и притом только одну.
Пусть A₁ A₂ A₃ … A_n – правильный многоугольник, О – центр описанной окружности.

В ходе доказательства предыдущей теоремы мы установили, что равны треугольники OA₂ A₃, OA₁ A₂ … OA₁ A_n. Поэтому высоты этих треугольников, проведённые из вершины О, также равны, то есть OH₁ = OH₂ = ⋯OH_n. Отсюда следует, что окружность с центром О и радиусом OH₁ проходит через точки H₁, H₂, … H_n и касается сторон многоугольника в этих точках, то есть эта окружность вписана в данный правильный многоугольник.
Докажем теперь единственность окружности. Предположим, что наряду с окружностью с центром О и радиусом OH₁ есть и другая окружность, вписанная в данный многоугольник. Тогда её центр O₁ равноудален от сторон многоугольника, то есть точка O₁ лежит на каждой из биссектрис углов многоугольника, и следовательно, совпадает с точкой О пересечения этих биссектрис. Радиус этой окружности равен расстоянию от точки О до сторон многоугольника, то есть равен OH₁. Таким образом, вторая окружность совпадает с первой. Теорема доказана.
Так как в равнобедренных треугольниках OA₂ A₃, OA₁ A₂ … OA₁ A_n проведенные высоты OH₁, OH₂, … OH_n являются и медианами, то имеет место следствие 1: окружность, вписанная в правильный многоугольник, касается сторон многоугольника в их серединах.
При доказательстве теоремы о вписанной в правильный многоугольник окружности было установлено следствие 2: центр окружности, описанной около правильного многоугольника, совпадает с центром окружности, вписанной в тот же многоугольник. Эта точка называется центром правильного многоугольника.
Докажем теперь единственность окружности. Рассмотрим какие-нибудь три вершины многоугольника, например, A₁, A₂, A₃. Так как через эти три точки проходит только одна окружность, то около многоугольника A₁ A₂ A₃ … A_n можно описать только одну окружность. Теорема доказана.
Рассмотрим задание из открытого банка ОГЭ.
ABCDEFGHI — правильный девятиугольник. Найдите угол EAI. Ответ дайте в градусах.

Найдем угол правильного девятиугольника, воспользовавшись выведенной формулой нахождения угла.
1) α_n = (n - 2)/n ∙ 180°
α₉ = (9 - 2)/9 ∙ 180° = 140°
Получаем, что угол правильного девятиугольника равен 140°.
Рассмотрим выпуклый шестиугольник AEFGHI. В нем четыре угла F, G, H, I по 140°, а оставшиеся углы равны между собой в силу того, что девятиугольник правильный.
Воспользуемся известной формулой для нахождения суммы углов выпуклого шестиугольника AEFGHI:
2) S_n = (n - 2) ∙ 180°
S₆ = (6 - 2) ∙ 180° = 720°.
Получаем, что сумма углов выпуклого шестиугольника равна 720°.
Для нахождения искомого угла нужно найти половину разности 720° и четырех углов по 140°.
3) ∠EAI = (720° - 4 • 140°)/2 = 80°
Ответ: 80°

В этом видеофрагменте мы вспомним, какую окружность называют вписанной в многоугольник. Докажем теорему об окружности, вписанной в правильный многоугольник. А также рассмотрим следствия из этой теоремы.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.

Получите невероятные возможности

Конспект урока "Окружность, вписанная в правильный многоугольник"

На этом уроке мы вспомним, какую окружность называют вписанной в многоугольник. Докажем теорему об окружности, вписанной в правильный многоугольник. А также рассмотрим следствия из этой теоремы.

Для начала давайте вспомним определение правильного многоугольника. Итак, правильным многоугольником называется выпуклый многоугольник, у которого все углы равны и все стороны равны. Так как у правильного многоугольника все углы равны, то угол правильного n-угольника можно вычислить по формуле: альфа энное равно 180 градусов умножить на эн минус два деленное на н, где n – количество сторон (углов) правильного n-угольника.

И вспомним еще определение вписанной окружности.

Определение. Окружность называется вписанной в многоугольник, если все стороны многоугольника касаются этой окружности. При этом многоугольник называется описанным около этой окружности.

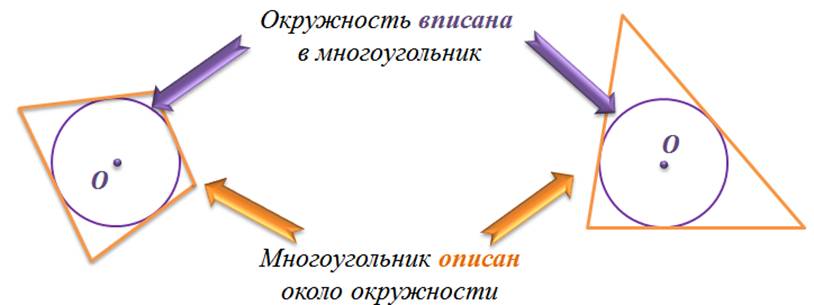
Ранее мы с вами рассматривали касание прямой и окружности.

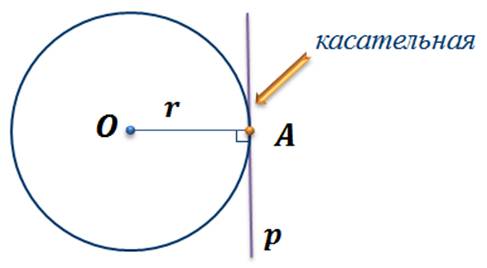
Напомню, что если задана окружность с центром в точке О и радиусом r, и точка А – общая точка прямой и окружности, то такая точка единственная. Прямая p, которая проходит через точку касания, называется касательной. Радиус OA, проведенный в точку касания, перпендикулярен касательной p.

Теорема. Отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.

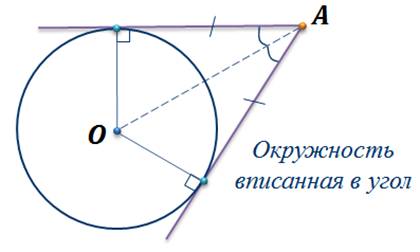
Значит, точка О – центр окружности – лежит на биссектрисе угла. Таким образом, имеем окружность, вписанную в угол.

Докажем теорему об окружности, вписанной в правильный многоугольник.

Теорема. В любой правильный многоугольник можно вписать окружность, и притом только одну.

Доказательство.

Пусть – правильный многоугольник.

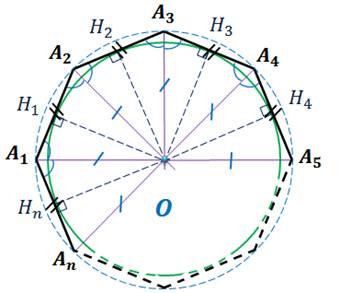
по двум сторонам и углу между ними.

Отсюда,.

Т.е. .

Следовательно, точка равноудалена от всех сторон многоугольника.

Если провести окружность с центром и , то все стороны многоугольника будут касаться окружности в этих точках.

Значит, в данный многоугольник можно вписать окружность.

Теперь докажем, что вписанная окружность только одна.

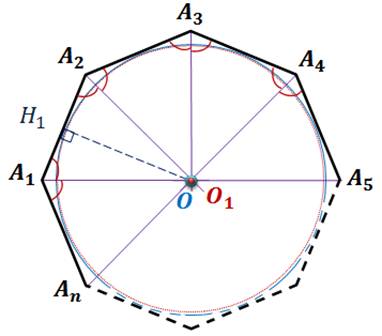
Предположим, что в то же время с окружностью с центром и радиусом существует и другая окружность.

Тогда ее центр лежит на каждой из биссектрис углов многоугольника.

Следовательно, ее центр совпадает с точкой пересечения этих биссектрис.

Радиус этой окружности равен расстоянию от точки до сторон многоугольника. Т.е. равен .Значит, вторая окружность совпадает с первой.

Теорема доказана.

Из этой теоремы вытекают следствия. Рассмотрим их.

Следствие 1. Окружность, вписанная в правильный многоугольник, касается сторон многоугольника в их серединах.

Доказательство.

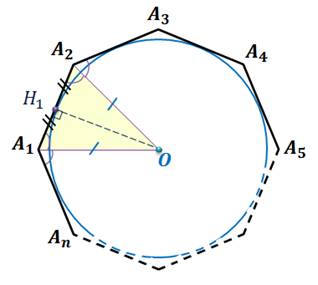
Пусть – правильный многоугольник.

– радиус вписанной в него окружности.

Рассмотрим .

Значит, – равнобедренный.

– по свойству касательной к окружности.

– высота .

– медиана по свойствам равнобедренного треугольника.

Следовательно, .

Что и требовалось доказать.

Следствие 2. Центр окружности, описанной около правильного многоугольника, совпадает с центром окружности, вписанной в тот же многоугольник.

Задача. В правильный четырехугольник вписана окружность. Определите ее радиус, если периметр правильного четырехугольника равен см.

Так как , то – квадрат.

Значит, (см).

(см).

Ответ: (см).

Подведем итоги урока. На этом уроке мы доказали теорему об окружности, вписанной в правильный многоугольник. А именно, доказали, что в любой правильный многоугольник можно вписать окружность, и притом только одну. А также вывели следствия из этой теоремы. Первое следствие: окружность, вписанная в правильный многоугольник, касается сторон многоугольника в их серединах. Второе следствие: центр окружности, описанной около правильного многоугольника, совпадает с центром окружности, вписанной в тот же многоугольник. Эта точка называется центром правильного многоугольника.

Правильный многоугольник -- выпуклый многоугольник, у которого все стороны и все углы равны между собой (Рис. 1).

Рисунок 1. Правильные многоугольники

Как мы знаем, сумма углов многоугольника находится по формуле$(n-2)\cdot ^0$

Значит, градусная мера одного угла правильного многоугольника равняется

Теорема об описанной около правильного многоугольника окружности

Около любого правильного многоугольника можно описать единственную окружность.

Доказательство.

Существование. Пусть нам дан правильный многоугольник $A_1A_2A_3\dots A_n$. Пусть биссектрисы углов $A_1\ и\ A_2$ пересекаются в точке $O$. Соединим с этой точкой все остальные вершины правильного многоугольника (Рис. 2).

Рисунок 2. Описанная вокруг правильного многоугольника окружность

Так как углы $A_1\ и\ A_2$ равны и $A_1O\ и\ A_2O$ -- биссектрисы, то угол $OA_1A_2$ равен углу $O_1$. Следовательно, треугольник $OA_1A_2$ равнобедренный, и, значит, $A_1O=A_2O$.

Так как $A_1A_2=A_2A_3$, $\angle O_1=\angle O_3$ и сторона $A_2O$ - общая, то треугольники $O_1$ и $O_3$ равны. Следовательно, $OA_2=OA_3$.

Аналогично доказывают другие равенства. В результате, будем иметь

То есть точка $O$ равноудалена от всех вершин многоугольника, а, значит, точка $O$ - центр описанной вокруг правильного многоугольника окружности.

Единственность. Рассмотрим три вершины многоугольника. Очевидно, что через них проходит только одна окружность, следовательно, вокруг правильного многоугольника можно описать только одну окружность.

Готовые работы на аналогичную тему

Теорема доказана.

Теорема вписанной в правильный многоугольник окружности

В любой правильный многоугольник можно вписать единственную окружность.

Доказательство.

Пусть нам дан правильный многоугольник $A_1A_2A_3\dots A_n$. Пусть точка $O$ - центр описанной вокруг данного многоугольника окружности (Рис. 3).

Рисунок 3. Вписанная в правильный многоугольник окружность

Так как $A_1A_2=A_2A_3$, $\angle O_1=\angle O_3$ и сторона $A_2O$ - общая, то треугольники $O_1$ и $O_3$ равны.

Аналогично доказывается равенство других треугольников. То есть, мы получим

Значит и высоты этих треугольников равны между собой

Тогда окружность с центром в точке $O$ и радиусом, равным $_1$ проходит через точки $H_1,\ H_2,\dots ,H_n$, то есть касается всех сторон данного многоугольника. Следовательно. Является вписанной для правильного многоугольника.

Единственность. Предположим противное. Пусть существует еще одна вписанная в этот многоугольник окружность. Обозначим её центр $O'$. Тогда $O'$ равноудалена от всех сторон многоугольника, а значит лежит в точке пересечения биссектрис его углов. Но тогда точка $O'$ совпадает с точкой $O$ и, следовательно, эти окружности также совпадают.

Теорема доказана.

Из этих двух теорем можно сформулировать следующие следствия:

Следствие 1: Вписанная в правильный многоугольник окружность касается его в серединах его сторон.

Следствие 2: Центр окружности, описанной около правильного многоугольника, совпадает с центром окружности, вписанной в этот же правильный многоугольник. Этот центр называется центром правильного многоугольника.

Формулы для правильного многоугольника

Дадим теперь несколько формул, относящихся к понятию правильного многоугольника (без их вывода).

Введем следующие обозначения. Пусть $S$ -- площадь правильного многоугольника, $P$ -- периметр правильного многоугольника, $a$ - сторона правильного многоугольника, $r$ - радиус вписанной в правильный многоугольник окружности, $R$ - радиус описанной около правильного многоугольника окружности. Тогда

Пример задачи на понятие правильного многоугольника

Чему равна сумма внешних углов правильного $n$-угольника. Если при каждой вершине взят только один внешний угол.

Решение.

Очевидно, что все внешние углы будут равны между собой и их количество равно $n$. Найдем один из них. Внешний угол $\beta $ многоугольника будет смежным с внутренним углом многоугольника. Используя формулу нахождения угла правильного $n$-угольника $\alpha =\frac^0(n-2)>$, получим

Правильные многоугольники

Наглядная геометрия 9 класс. Опорный конспект 4. Правильные многоугольники

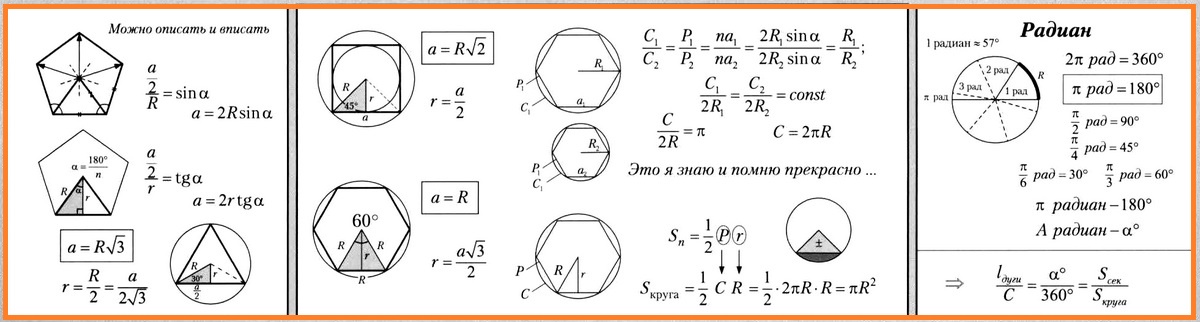
Правильный многоугольник — это такой многоугольник, у которого все стороны и все углы равны. Равносторонний треугольник и квадрат — правильные многоугольники. Если разделить окружность на п равных частей и соединить соседние точки отрезками, то получим правильный многоугольник. Вокруг всякого правильного многоугольника можно описать окружность, в него также можно вписать окружность, и центры этих окружностей совпадают.

Мы научимся строить правильный треугольник, правильный четырехугольник (квадрат) и правильный шестиугольник при помощи циркуля и линейки и выведем формулы, связывающие радиусы вписанной и описанной окружностей с длиной стороны правильного многоугольника.

Если число сторон вписанного правильного многоугольника увеличивать, то его периметр будет стремиться к длине окружности, а площадь — к площади круга. Отсюда можно получить формулы длины окружности и площади круга: С = 2πR и S = πR 2 .

Вы знаете, что углы измеряются в градусах. Градус, как известно, равен 1/180 части развернутого угла. Мы познакомимся еще с одной очень важной единицей измерения углов, которая связана с окружностью, — 1 радианом. 1 рад = 57°.

1. Правильный многоугольник. Теорема об описанной и вписанной окружностях.

Правильным называется многоугольник, у которого все стороны и углы равны.

Теорема. Вокруг всякого правильного многоугольника можно описать окружность. Во всякий правильный многоугольник можно вписать окружность. Центры этих окружностей совпадают.

Доказательство. Проведем биссектрисы двух углов правильного многоугольника. Получим равнобедренный треугольник (углы при основании равны как половины равных углов). Соединив точку пересечения биссектрис с третьей вершиной многоугольника, получим треугольник, равный 1-му (по двум сторонам и углу между ними). Продолжая соединять эту точку с остальными вершинами, получим множество равных равнобедренных треугольников. Тогда полученная точка равноудалена от всех вершин правильного многоугольника. Значит, она — центр описанной окружности. Так как высоты этих треугольников, опущенные на их основания, равны, то данная точка равноудалена и от сторон правильного многоугольника. Значит, она — центр вписанной окружности.

2. Выражение стороны а через R и r для правильного n-угольника.

Соединим центр правильного многоугольника с двумя соседними вершинами. Получим равнобедренный треугольник с углом при вершине, равным 360°/n. Половина его равна 180°/n, где n — число сторон. Из прямоугольного треугольника находим:

3. Выражение R и r через сторону а для правильного 3-угольника.

4. Выражение R и r через сторону а для правильного 4-угольника.

5. Выражение R и r через сторону а для правильного 6-угольника.

6. Формула длины окружности. Вывод.

Теорема. Длина окружности С = 2πR.

Доказательство. Рассмотрим ДВА правильных вписанных многоугольника с одинаковым числом сторон n. При увеличении числа сторон их периметры Р₁ и Р₂ будут стремиться к длинам окружностей, т. е. к С₁ и С₂. Поэтому

7. Формула площади круга. Вывод.

Теорема. Площадь круга S = πR 2 .

8. Длина дуги и площадь сектора.

Длина дуги и площадь сектора пропорциональны градусной мере дуги или центрального угла сектора:

Формулы длины дуги и площади сектора не нужно запоминать — они находятся из логически понятной пропорции:

а) длина дуги составляет от длины окружности такую же часть, какую составляет ее градусная мера от 360°;
б) площадь сектора составляет от площади круга такую же часть, какую составляет его центральный угол (его дуга) от 360°.

9. Площадь сегмента.

Площадь сегмента равна площади сектора минус или плюс площадь равнобедренного треугольника, образованного радиусами этого сектора. Минус — если центральный угол сектора меньше 180°, и плюс — если больше 180°. Если центральный угол равен 180°, то этот сегмент — полукруг, и его площадь равна πR 2 /2.

10. Радианная мера угла.

Радианом называется центральный угол, опирающийся на дугу окружности, равную 1 радиусу.

Так как длина окружности С = 2πR, то в окружности укладывается 2π радиусов (≈ 6,28 радиуса), а в полуокружности — π радиусов (≈3,14 радиуса).

2π радиан = 360°. ⇒ π радиан = 180°. ⇒ 1 радиан = 180°/π ≈ 57°

11. Перевод градусной меры угла в радианную и наоборот.

ЭТО НУЖНО ЗНАТЬ !

Читайте также: