Сформулируйте и докажите теорему выражающую третий признак подобия треугольников кратко

Обновлено: 02.07.2024

В этом уроке познакомимся с третьим признаком подобия треугольников и рассмотрим задачу на его применение.

Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого.

Число, равное отношению сходственных сторон подобных треугольников, называют коэффициентом подобия.

Третьим признаком подобия треугольников является следующее утверждение:

Tсли три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.

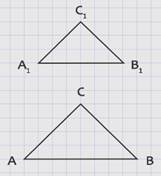
Рассмотрим АВС2, у которого ∠1 = ∠А1 , ∠2 = ∠В1.

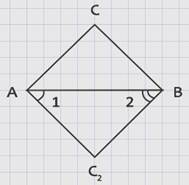
∆АВС2 и ∆А1В1С1 подобны по первому признаку подобия треугольников (так как два угла одного треугольника соответственно равны двум углам другого). Поэтому:

По условию теоремы:

Из последних двух равенств стороны ВС и ВС2; АС и АС2 равны между собой.

Рассмотрим треугольники АВС и АВС2.

Они равны по трем сторонам (АВ – общая сторона, ВС = ВС2 , АС = АС2).

Из равенства треугольников АВС и АВС2 следует, что ∠А = ∠1, а так как ∠1 = ∠А1, то ∠А = ∠А1.

Что и требовалось доказать.

В прямоугольном треугольнике АВС катет АВ = 3 см, гипотенуза АС = 5 см.

Катеты МК и КР треугольника МКР равны √27 см и 4√3 см.

Подобны ли эти треугольники?

Найдем в каждом из этих треугольников неизвестные стороны.

Оказалось, что стороны треугольника АВС пропорциональны сторонам треугольника МКР, значит, данные треугольники подобны по третьему признаку подобия.

Дано: ΔABC, ΔA₁B₁C₁,

$\frac<<AB> >> = \frac>> = \frac>>$

1) Отложим на луче A₁B₁ отрезок A₁B₂, A₁B₂=AB.

2) Через точку B₂ проведём прямую B₂С₂, параллельную прямой B₁C₁.

Из подобия треугольников следует пропорциональность соответствующих сторон:

$\frac<<A_1 B_2 > >> = \frac>> = \frac>>.$

$\frac<<AB> >> = \frac>> = \frac>>.$

Так как по условию

$\frac<<AB> >> = \frac>> = \frac>>,$

Геометрия:

Контакты

Теорема 1. Первый признак подобия треугольников. Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.

Доказательство. Пусть ABC и $А_1В_1С_1$ — треугольники, у которых $\angle A = \angle A_1 ; \angle B = \angle B_1$ , и, следовательно, $\angle C = \angle C_1$ . Докажем, что $\triangle ABC \sim \triangle A_1B_1C_1$ (рис.1).

Отложим на ВА от точки В отрезок $ВА_2$, равный отрезку $A_1B_1$ , и через точку $А_2$ проведем прямую, параллельную прямой АС. Эта прямая пересечет ВС в некоторой точке $С_2$ . Треугольники $А_1В_1С_1\text< и >А_2ВС_2$ равны: $А_1В_1 = А_2В$ по построению, $\angle В = \angle В_1$ по условию и $\angle А_1 = \angle А_2$ , так как $\angle А_1 = \angle А$ по условию и $\angle А = \angle А_2$ как соответственные углы. По лемме 1 о подобных треугольниках имеем: $\triangle A_2BC_2 \sim \triangle ABC$ , и значит, $\triangle ABC \sim \triangle A_1B_1C_1$ . Теорема доказана.

По аналогичной схеме устанавливаются теоремы 2 и 3.

Теорема 2. Второй признак подобия треугольников. Если две стороны одного треугольника соответственно пропорциональны двум сторонам другого треугольника и углы между этими сторонами равны, то треугольники подобны.

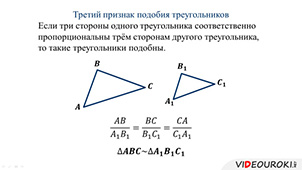
Теорема 3. Третий признак подобия треугольников. Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.

Из теоремы 1 вытекает следующее.

Следствие 1. В подобных треугольниках сходственные стороны пропорциональны сходственным высотам, т. е. тем высотам, которые опущены на сходственные стороны.

Пример 1. Подобны ли два равносторонних треугольника?

Решение. Так как в равностороннем треугольнике каждый внутренний угол равен 60° (следствие 3), то два равносторонних треугольника подобны по первому признаку.

Пример 2. В треугольниках ABC и $А_1В_1С_1$ известно, что $\angle A = \angle A_1 ; \angle B = \angle B_1 ; АВ = 5 м, ВС = 7 м, А_1В_1 = 10 м, А_1С_1 = 8 м.$ Найти неизвестные стороны треугольников.

Решение. Треугольники, определенные условием задачи, подобны по первому признаку подобия. Из подобия треугольников следует: $$ \frac = \frac = \frac \,\,\, (1) $$ Подставив в равенство (1) данные из условия задачи, получим: $$ \frac = \frac = \frac \,\,\, (2) $$ Из равенства (2) составим две пропорции $$ \frac = \frac \\ \frac = \frac \\ \text< откуда >В_1С_1 = 14 (м), АС = 4 (м). $$

Пример 3. Углы В и $В_1$ треугольников ABC и $А_1В_1С_1$ равны. Стороны АВ и ВС треугольника ABC в 2,5 раза больше сторон $A_1B_1$ и $B_1C_1$ треугольника $A_1B_1C_1$. Найти АС и $A_1C_1$ , если их сумма равна 4,2 м.

Решение. Пусть условию задачи отвечает рисунок 2.

Из условия задачи: $$ 1) \angle B = \angle B_1 ; \\ 2) \frac = \frac = 2,5 \\ 3) AC + A_1C_1 = 4,2 м. $$ Следовательно, $\triangle ABC \sim \triangle А_1В_1С_1$. Из подобия этих треугольников следует $$ \frac = 2,5\text< , или >АС = 2,5\bullet А_1С_1 $$ Так как АС = 2,5 • А₁С₁, то АС + А₁C₁ = 2,5 • А₁С₁ + A₁C₁ = 4,2, откуда A₁C₁ = 1,2 (м), АС = 3 (м).

Пример 4. Подобны ли треугольники ABC и А₁В₁С₁, если АВ = 3 см, ВС = 5 см, АС = 7 см, А₁В₁ = 4,5 см, B₁C₁ = 7,5 см, A₁C₁ = 10,5 см?

Решение. Имеем: $$ \frac = \frac = \frac \\ \frac = \frac = \frac \\ \frac = \frac = \frac $$ Следовательно, треугольники подобны по третьему признаку.

Пример 5. Доказать, что медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины.

Решение. Рассмотрим произвольный треугольник ABC. Обозначим буквой О точку пересечения его медиан $АА_1\text< и >ВВ_1$ и проведем среднюю линию $A_1B_1$ этого треугольника (рис.3).

Отрезок $A_1B_1$ параллелен стороне АВ, поэтому $\angle 1 = \angle2 \text < и >\angle 3 = \angle 4 $. Следовательно, треугольники АОВ и $A_1OB_1$ подобны по двум углам, и, значит, их стороны пропорциональны: $$ \frac = \frac = \frac $$

Но $AB = 2A_1B_1$ , поэтому $AO = 2A_1O$ и $BO = 2B_1O$ .

Аналогично доказывается, что точка пересечения медиан $BB_1\text< и >CC_1> делит каждую из них в отношении 2:1, считая от вершины, и, следовательно, совпадает с точкой О.

Итак, все три медианы треугольника ABC пересекаются в точке О и делятся ею в отношении 2:1, считая от вершины.

Замечание. Ранее отмечалось, что биссектрисы треугольника пересекаются в одной точке, серединные перпендикуляры к сторонам треугольника пересекаются в одной точке. На основе последнего утверждения устанавливается, что и высоты треугольника (или их продолжения) пересекаются в одной точке. Эти три точки и точка пересечения медиан называются замечательными точками треугольника .

Пример 6. Проектор полностью освещает экран А высотой 90 см, расположенный на расстоянии 240 см. На каком наименьшем расстоянии в см. от проектора нужно расположить экран Б, высотой 150 см, так, что бы он был полностью освещён, если настройки проектора остаются неизменными.

Видео-решение.

В этом уроке мы сформулируем и докажем третий признак подобия треугольников. Убедимся, что третий признак подобия позволяет сделать вывод о подобии треугольников по пропорциональности их сторон. А также выполним несколько практических упражнений на закрепление изученного материала.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.

Получите невероятные возможности

Конспект урока "Третий признак подобия треугольников"

Прежде, чем познакомиться с третьим признаком подобия треугольников, вспомним известные нам первый и второй.

Итак, первый признак подобия треугольников: если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.

Второй признак подобия треугольников: если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы между ними равны, то такие треугольники подобны.

Ну а теперь сформулируем третий признак подобия треугольников.

Теорема (3-й признак подобия треугольников). Если три стороны одного треугольника соответственно пропорциональны трём сторонам другого треугольника, то такие треугольники подобны.

Доказательство.

, , тогда по 1-му признаку.

Получаем, что , .

Тогда по 3-му признаку.

Следовательно, .

Так как , то .

Следовательно, .

Что и требовалось доказать.

Давайте найдём среди следующих треугольников подобные.

У каждого из треугольников известны длин трёх его сторон, а тогда воспользуемся только что доказанным третьим признаком подобия треугольников.

Посмотрим внимательно на значения их длин и заметим, что стороны треугольника а пропорциональны сторонам треугольника в, а значит, эти треугольники подобны. При этом коэффициент подобия равен 2.

Задача. Подобны ли треугольники и , если см, см, см, см, см, см?

Значит, .

Следовательно, .

Ответ: .

Задача. Докажите, что прямоугольные треугольники и подобны, если стороны и треугольника соответственно равны см и см, а стороны и треугольника соответственно равны см и см.

(см).

, ,

(см).

; ; .

Значит, .

Следовательно, по 3-му признаку.

Что и требовалось доказать.

Итак, сегодня на уроке мы познакомились с ещё одним признаком подобия треугольников: если три стороны одного треугольника соответственно пропорциональны трём сторонам другого треугольника, то такие треугольники подобны.

Читайте также: