Сформулируйте и докажите теорему о вычислении площади треугольника кратко

Обновлено: 04.07.2024

Существует несколько формул для нахождения площади треугольника. В зависимости от известных данных нужно выбрать одну из них.

Площадь треугольника через высоту и основание

Этот способ нахождения площади треугольника изучают на уроках геометрии в 8 классе и используют чаще всего.

Площадь треугольника равна половине произведения высоты на основание, к которой проведена эта высота.

где S — площадь треугольника,

а — длина основания,

h — высота, проведенная к а.

Следствия теоремы:

У прямоугольного треугольника один катет можно принять за основание, а второй — за высоту.
Если у двух треугольников высоты равны, то отношение между их площадями равно отношению между основаниями.

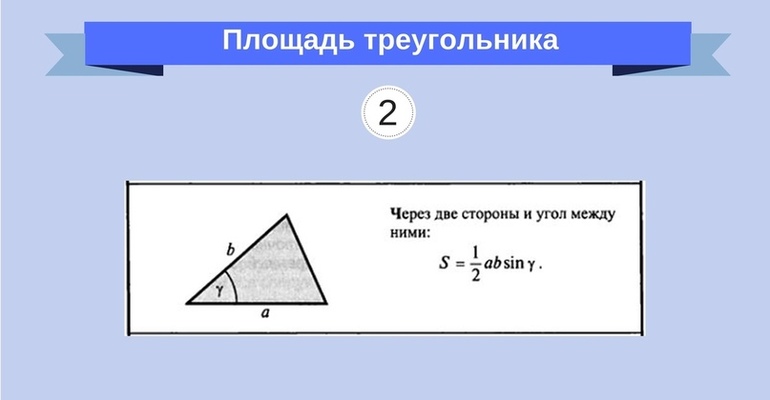
Нахождение площади треугольника по двум сторонам и углу между ними

В вычислении используется синус угла. Данный способ применяют после знакомства с этим понятием в 9 классе.

Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.

где S — площадь треугольника,

a и b — его стороны,

γ — угол между a и b.

Формула Герона

Если у треугольника известны длины трех сторон, то его площадь можно найти по формуле Герона.

S = p p - a p - b p - c

где S — площадь треугольника,

a, b, с — его стороны,

р — полупериметр, р = a + b + c 2 .

Площадь треугольника по радиусу описанной окружности

Площадь треугольника можно вычислить, зная три его стороны и радиус описанной окружности.

где S — площадь треугольника,

R — радиус окружности, описанной около данного треугольника,

a, b, c — стороны треугольника.

Также площадь треугольника можно найти, если известны радиус описанной окружности и величины трех углов треугольника.

S = 2 R 2 · s i n ∠ A · s i n ∠ B · s i n ∠ C

где S — площадь треугольника,

∠A, ∠B, ∠С — углы треугольника,

R — радиус описанной окружности.

Площадь треугольника по радиусу вписанной окружности

Площадь треугольника равна произведению полупериметра на радиус вписанной окружности.

где S — площадь треугольника,

r — радиус вписанной окружности,

р — полупериметр, вычисляем по формуле р = a + b + c 2 .

Понятие подобия треугольников

Подобные треугольники — это такие треугольники, у которых углы попарно равны, а лежащие напротив равных углов стороны пропорциональны. Эти стороны называются сходственными.

У подобных треугольников соответственно пропорциональны также медианы, высоты, биссектрисы, периметры. Соотношение между этими величинами равно коэффициенту подобия.

Коэффициент подобия — это отношение между периметрами двух подобных треугольников.

Отношение между площадями подобных треугольников равно коэффициенту подобия в квадрате.

Доказательство:

Пусть ΔDEF подобен ΔKMN, записывают ΔDEF∼ΔKMN.

Следовательно, DE:KM=EF:MN=DF:KN=k, где k — коэффициент подобия ΔDEF и ΔKMN.

Если у двух треугольников равны углы, то их площади соотносятся как произведение сторон, заключающих данные углы.

S D E F S K M N = D E × D F K M × × N = D E K M × D F K N = k · k = k 2 .

Задачи на применение теоремы для 9 класса

Рассмотрим решения задач, которые помогут в самостоятельном выполнении заданий.

Дано: два подобных треугольника. Коэффициент подобия между ними равен 2 .

Найти: отношение между площадями этих треугольников.

Решение: в соответствии с изученной теоремой о соотношении площадей подобных треугольников

S 1 S 2 = k 2 = 2 2 = 2 .

Ответ: S 1 S 2 = 2 .

Дано: Два треугольника подобны. ΔDEF∼ΔKMN. Их площади равны 500 с м 2 и 125 с м 2 . S Δ D E F = 500 с м 2 , S Δ K M N = 125 с м 2 . Сторона DE равна 18 см.

Найти: сходственную ей сторону КМ.

Решение:

Вычислим отношение между S D E F и S K M N :

S D E F S K M N = 500 125 = 4 .

Согласно теореме о соотношении площадей подобных треугольников k 2 = 4 , а k = 2 .

Из подобия треугольников следует, что D E K M = 2 ⇒ K M = D E : 2 = 18 : 2 = 9 ( с м ) .

Ответ: КМ=9 см.

Дано: треугольник Δ O P Q , S Δ O P Q равна 12 с м 2 . Параллельно стороне OQ в ΔOPQ проведена средняя линия KM.

Найти: S треугольника, образованного средней линией KM и сторонами OP и PQ треугольника OPQ, то есть площадь ΔKPM.

Решение:

ΔOPQ и ΔKPM подобны, так как равны их углы.

∠P — общий, ∠POQ=∠PKM и ∠PQO=∠PMK как соответственные углы при параллельных прямых и секущей.

Сходственные стороны ΔOPQ и ΔKPM пропорциональны, коэффициент пропорциональности равен 2, так как согласно теореме о средней линии треугольника K M = O Q 2 .

Применим теорему об отношении площадей подобных треугольников: S Δ O P Q S Δ K P M = 2 2 = 4 ,

Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.

Вывод формулы с доказательством

Для доказательства теоремы возьмем произвольный треугольник ABC.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Пусть BC = a, CA = b, S — площадь треугольника ABC.

Докажем, что \(S=\frac12ab\cdot\sin C\)

Введем координатную плоскость и впишем в нее треугольник ABC так, чтобы:

точка C совпадала с началом координат;
точка B лежала на положительной оси Cx;
точка A находилась в верхней полуплоскости.

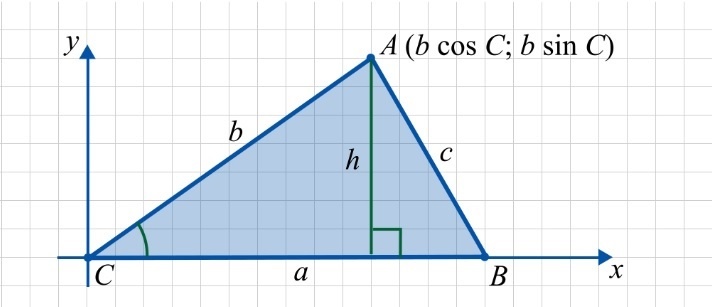
С учетом описанных условий вычисление площади треугольника можно произвести по формуле:

где h — высота треугольника. В данном случае h равна ординате точки A.

Получается, что \(h=b\cdot\sin C.\)

Это связано с тем, что \(\sin C\) равен отношению противолежащего катета (то есть h) к гипотенузе (то есть к b):

Отсюда выражаем h и получаем:

Как следствие \(S=\frac12ab\cdot\sin C\) , то есть вместо \(h\) подставляем \(b\cdot\sin C\) . Теорема геометрии доказана.

Пример решения задачи

Задача

Дан прямоугольный треугольник \(ABC\) , где \(AB = 3\) , \(AC = 4\) , \(\angle A=30\) .

Найти площадь треугольника.

Решение

Для того чтобы найти площадь треугольника, воспользуемся ранее доказанной теоремой.

В формулу \(S=\frac12AB\cdot AC\cdot\sin A\) подставляем записанные выше исходные показатели и производим расчет.

1 Расскажите, как измеряются площади многоугольников.

2 Сформулируйте основные свойства площадей многоугольников.

3 Сформулируйте и докажите теорему о вычислении площади прямоугольника.

4 Сформулируйте и докажите теорему о вычислении площади параллелограмма.

5 Сформулируйте и докажите теорему о вычислении площади треугольника. Как вычислить площадь прямоугольного треугольника по его катетам?

6 Сформулируйте и докажите теорему об отношении площадей двух треугольников, имеющих по равному углу.

7 Сформулируйте и докажите теорему о вычислении площади трапеции.
8 Сформулируйте и докажите теорему Пифагора.
9 Сформулируйте и докажите теорему, обратную теорему Пифагора.
10 Какие треугольники называются пифагоровыми? Приведите примеры пифагоровых треугольников?

1. Если многоугольник произвольный, то из одной вершины проведите все диагонали и найдите площадь каждого получившегося треугольника. Результаты сложите. Если многоугольник правильный, то существуют формулы для каждого отдельного случая. Но можно вывести и общую формулу, зависящую от количества сторон.
2. Площадь многоугольника есть положительная величина со следующими свойствами:
I. Равные многоугольники имеют равные площади.
II. Если многоугольник составлен из двух многоугольников, не имеющих внутренних общих точек, то его площадь равна сумме площадей этих многоугольников.
III.Площадь квадрата со стороной, равной единице длины, равна 1 (единице измерения площадей)
3. Площадь прямоугольника равна произведению его сторон
Док-во:
Пусть у прямоугольника длины сторон а и b. Достроим его до квадрата со стороной a+b. Т. е. его площадь (квадрата) равна (a+b)^2. С другой стороны эта площадь равна сумме квадрата со стороной а, квадрата со сторой b и двух прямоугольников со сторонами а и b (которую мы и доказаываем). Обозначим ее S и приравняем площадь квадрате со стороной a+b к сумме площадей "маленьких прямоугольников и квадратов".
(a+b)^2=S+S+a^2+b^2
a^2+b^2+2ab=a^2+b^2+2S
2ab=2S
S=ab. Доказано
4. Sabcd=a*h ( Площадь паралелограмма равна произведению его основания на высоту)
Если BF и CM - перпендикуляры к прямой AD, то треугольник ABF=треугольнику DCE
(так как AB=DC и проекция AF=DM). Поэтому площади этих треугольников равны. Площадь паралеллограмма ABCD равна сумме двух фигур: треугольника ABF (равного треугольникуDCM) и трапеции FBCD. Значит, если от площади ABCD вычесть площадь треугольника ABF, получим площадь трапеции FBCD. Тогда площадь параллелограмма ABCD равна площади прямоугольника FBCM. А стороны этого прямоугольника равны BC=AD=а и BF=h.
S ABCD = AD•BF=a•h.
5. площадь прямоугольного треугольника это половина площи прямоугольника т. е. S=ab. то Sтр=ab/2.
или ch\2. т. к. у прямоугольного треугольника произведение катетов равно произведению высоты на гипотенузу
6. Если угол одного треугольника равен углу другого треугольника, то отношение площадей этих треугольников равно отношению произведений сторон, заключающих равные углы.
7. Площадь трапеции равна произведению полусуммы оснований на высоту, проведенную к основаниям. Проведя две высоты получим прямоугольник, со сторонами a и h, и два прямоугольных треугольника, с катетами p и q, такими, что a+p+q=b. S=ah+ph/2+qh/2=(2a+p+q)h/2=(a+(a+p+q))h/2=(a+b)h/2. Quod errat demonstrandum
8. ФормулировкиТеорема Пифагора: Сумма площадей квадратов, опирающихся на катеты (a и b), равна площади квадрата, построенного на гипотенузе (c).Геометрическая формулировка: Изначально теорема была сформулирована следующим образом: Впрямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах. Алгебраическая формулировка: В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. То есть, обозначив длину гипотенузы треугольника через, а длины катетов через и :Обе формулировки теоремы эквивалентны, но вторая формулировка более элементарна, она не требует понятия площади. То есть второе утверждение можно проверить, ничего не зная о площади и измерив только длины сторон прямоугольного треугольника.

9. Теорема.
Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный.
Доказательство.
Пусть треугольнике АВС АВ^2=АС^2+ВС^2. Докажем, что угол С прямой. Рассмотрим прямоугольнй треугольник А1В1С1 с прямым углом С1, у которого А1С1=АС и В1С1=ВС. По теореме Пифагора А1В1^2=А1С1^2+В1С1^2, и, значит, А1В1^2=АС^2+ВС^2. Но АС^2+ВС^2=АВ^2, откуда А1В1=АВ
Треугольники АВС и А1В1С1 равны по трем сторонам, поэтому Айна Шихмурзаева Ученик (136) 3 года назад

В начале урока мы повторим известные нам формулы для вычисления площади треугольника, а затем выведем еще одну формулу, которая позволяет найти площадь треугольника, зная две стороны и синус угла между ними. Также получим формулу для вычисления площади параллелограмма. Рассмотрим примеры применения этих формул.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.

Получите невероятные возможности

Конспект урока "Теорема о площади треугольника"

Мы с вами уже знаем несколько формул для вычисления площади треугольника. Давайте вспомним их. Если мы знаем длину одной из сторон треугольника и длину высоты, проведенной к этой стороне, то площадь треугольника можно найти как половина произведения этих длин .

Например, найдем площадь треугольника, показанного на рисунке при h= 6, а a=5. Площадь этого треугольника .

Если треугольник прямоугольный, то его площадь находится как половина произведения катетов

Например, найдем площадь прямоугольного треугольника с катетами равными 4 и 9. Площадь .

Если нам известны длины всех сторон треугольника, то площадь можно вычислить по формуле Герона, где p – полупериметр треугольника.

Найдем, например, площадь треугольника со сторонами 13, 14 и 15 сантиметров. Полупериметр этого треугольника . Тогда площадь этого треугольника по формуле Герона
.

Сегодня на уроке мы с вами познакомимся еще с одной формулой, но сначала давайте вспомним формулу для координат произвольной точки А, расположенной в верхней полуплоскости.

Рассмотрим произвольный треугольник ABC со сторонами a, b, c и углами α, β, γ.

Докажем, что площадь треугольника вычисляется по формуле .

Расположим треугольник ABC в координатной плоскости так, чтобы точка C совпадала с началом координат, а точка B лежала на положительной полуоси Cx, а точка А имела положительную ординату, то есть располагалась в верхней полуплоскости.

Опустим из точки А высоту h. Площадь этого треугольника равна половине произведения стороны a на h. Координаты точки А равны
.

Высота h будет равна ординате точки А, то есть равна произведению длины стороны АC на синус угла γ, или .

Таким образом, мы доказали теорему. Сформулируем ее.

Теорема. Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.

Нетрудно убедиться, что если с началом координат совместить точку А, точку C расположить на положительном полуоси Ax, а точку B расположить в верхней полуплоскости, то можно записать, что площадь треугольника .

Если же с началом координат совместить точку B, точку А расположить на положительной полуоси Bx, а точку C расположить в верхней полуплоскости, тогда площадь треугольника .

Нетрудно заметить, что формула для вычисления площади прямоугольного треугольника является частным случаем этой формулы. Рассмотрим прямоугольный треугольник. Применяя общую формулу для вычисления площади треугольника, получим, что площадь этого . Угол C – прямой, его синус равен 1, то есть площадь прямоугольного треугольника равна половине произведения катетов . Мы получили, уже известную нам формулу.

Решим несколько задач.

Задача. Найти площадь треугольника если:

а) , ; б) , ;

в) , .

Запишем формулу для вычисления площади треугольника.

а)

б)

в)

Поскольку 46 – не табличное значение, то можно оставить в таком виде. Или с помощью калькулятора найти приближенное значение синуса 46°. Тогда получим, площадь треугольника приблизительно равна 40,28 сантиметрам квадратным.

Задача. . Найти , если , .

Теперь давайте рассмотрим параллелограмм ABCD.

Проведем диагональ АC. Эта диагональ делит параллелограмм на два треугольника. Легко увидеть, что эти треугольники равны по третьему признаку (стороны AB и CD, АD и BC равны по свойству сторон параллелограмма, АC – общая). Площадь треугольника ABC можно найти по формуле: . Площадь треугольника ACD можно найти по формуле: . Тогда площадь параллелограмма равна сумме площадей этих треугольников .

, .

То есть, другими словами, площадь параллелограмма равна произведению двух его смежных сторон на синус угла между ними.

И опять, как в случае с треугольником, формула для вычисления площади прямоугольника является частным случаем формулы для вычисления площади параллелограмма. Прямоугольник – параллелограмм, углы которого равны 90°.

Обратите внимание, что угол между сторонами параллелограмма можно записать так.

Задача. Найти площадь параллелограмма если:

, .

Задача. Соседние стороны параллелограмма равны , . Какой угол должен быть между ними, чтобы площадь параллелограмма была наибольшей?

Таким образом мы получили, что наибольшей будет площадь прямоугольника со сторонами a и b.

Задача. Найти площадь ромба, если его стороны равны , а один из углов равен .

Ромб – параллелограмм, значит, для вычисления площади ромба мы можем использовать формулу для вычисления площади параллелограмма.

Задача. Площадь треугольника равна . Сторона в 2 раза больше стороны . Найти .

Подведем итоги урока:

Сегодня на уроке, мы вспомнили формулы для вычисления площади треугольника, а также познакомились с новой. Мы познакомились с формулой вычисления площади параллелограмма. Рассмотрели примеры применения этих формул.

Одно из базовых понятий геометрии — это площадь фигуры. В процессе изучения курса школьной математики оно вводится весьма рано и под ним понимают область, ограниченную произвольным многоугольником. Однако найти её бывает весьма проблематично, и для упрощения задачи вначале чаще всего рассматривают не произвольные фигуры, а их частные случаи. Наглядным примером является прямоугольный треугольник.

Поиск площади

Найти площадь такого треугольника по двум сторонам не составит труда. Если это катеты, их надо перемножить и полученный результат разделить на 2. Если дана гипотенуза, придётся прибегнуть к помощи теоремы Пифагора и, используя её, сначала найти недостающий катет. Однако не всегда по условию рассматриваются частные случаи фигур: чем сложнее становится задачи, тем реже они встречаются. И при рассмотрении произвольных многоугольников обычно прибегают к теореме о площади через синус угла.

Две стороны.
Размерность угла между ними.

Сумма всех углов равна 180 градусов, это позволит, найти третий путём вычитания от 180 2 известных. Также может пригодиться определение косинуса и синуса. Косинус равен отношению прилежащего катета к гипотенузе, в то время как синус равен отношению противолежащего катета к гипотенузе.

Используя эти определения, можно найти недостающую сторону, если по условию задачи она не дана сразу.

Доказательство теоремы

Теорема остаётся просто предположением, пока не будет доказана, поэтому самое время перейти к доказательству. Площадь прямоугольного треугольника можно найти, как произведение катетов, делённое на 2. Если он таковым не является, это не помешает использовать этот факт для доказательства, но для начала нужно ввести общие обозначения.

A, B, C — вершины. При указании углов будут иметься ввиду углы при них.
a, b, c — стороны, лежащие напротив соответствующих вершин.

Очевидно, что в любом треугольнике будет хотя бы 2 острых угла, градусная мера которых меньше 90. Доказать утверждение можно от обратного. Если только один из них острый, 2 остальных должны быть равны или больше 90 градусам, то есть быть прямыми или тупыми. Тогда их сумма равна или больше 180 градусов. Что противоречит тому, что сумма всех трёх равна 180.

Вывод — предположение было неверное, следственно в любом треугольнике обязательно есть хотя бы 2 острых угла.

Следующий шаг — опустить высоту из неострого угла. Используя это дополнительное построение, можно получить 2 прямоугольных треугольника, у которых одна сторона (высота) является общей. Теперь можно найти площадь изначальной фигуры, как сумму двух полученных треугольников. Получается формула для нахождения площади — S = 0.5*a*h. Где h — высота, a — сторона, на которую она была опущена.

Теперь можно применить определение синуса и найти высоту — h = c*sin (b). Где h — проведённая ранее высота, c — одна из сторон, sin (b) — синус угла, примыкающего к основанию, на которое была опущена высота.

Полученное значение высоты нужно подставить в изначальную формулу и получить выражение: S = 0.5*a*c*sin (b). Таким образом, площадь равна половине произведения сторон на синус угла между ними. Что и требовалось доказать.

Читайте также: