Распределение максвелла и больцмана кратко

Обновлено: 05.07.2024

Мы установили функцию, описывающую распределение молекул по скоростям (распределение Максвелла), и зависимость, характеризующую распределение молекул по значениям потенциальной энергии (распределение Больцмана). Обе зависимости можно объединить в одно обобщенное распределение.

Рассмотрим бесконечно малый объем dV газа, расположенный в точке с радиусом-вектором в большой системе, представляющей идеальный газ при постоянной температуре во внешних силовых полях. Число молекул в выделенном объеме есть n( ) d 3 r. Поскольку объем невелик, в его пределах плотность частиц можно считать постоянной. Это означает, что выполнено условие справедливости распределения Максвелла. Тогда для числа молекул dN, имеющих скорости от v до v + dv и находящихся в объеме d 3 r, в результате объединения зависимостей (3.11) и (3.27), получаем следующую формулу:

Но концентрация молекул n(r) зависит от расположения этого объема во внешних силовых полях:

где n₀ — концентрация молекул в точке, где Е_p = 0. Тогда

представляет собой полную энергию частицы во внешнем потенциальном силовом поле, мы приходим к обобщенному распределению Максвелла — Больцмана по энергиям молекул:

где N — полное число частиц в системе, a dN — число частиц с координатами между r и r + dr и (одновременно) со скоростями между v и v + dv.

Средняя энергия квантового осциллятора. Распределение Максвелла — Больцмана было получено в классической физике, но оно оказалось справедливым и в квантовой механике, где были подвергнуты пересмотру многие казавшиеся незыблемыми положения. В качестве примера рассмотрим задачу о грузе массой т, закрепленном на конце пружинки с жесткостью k. Уравнение движения хорошо известно, и его решением являются гармонические колебания тела с круговой частотой

Классическая энергия системы, моделирующей колебания атомов в молекуле дается формулой (3.62) и может принимать любые значения в зависимости от амплитуды колебаний. Как нам известно из квантовой механики, энергия колебаний квантуется, то есть принимает дискретный ряд значений, определяемых формулой:

В соответствии с общими принципами статистической физики вероятность Р_n найти осциллятор в состоянии, характеризуемом неким значением n колебательного квантового числа, определяется формулой

где А — нормировочная постоянная. Для ее определения надо воспользоваться условием нормировки вероятности

Для этого в известную формулу для геометрической прогрессии

Получаем тогда вместо (2)

откуда следует выражение для постоянной А. Используя его в выражении (1), приходим к вероятности

Видно, что чем больше значение квантового числа n, тем меньше вероятность обнаружить осциллятор в таком состоянии. Чем выше температура, тем большие значения n становятся практически значимыми для системы. При

к нулю стремятся все вероятности Р_n с n > 1, и лишь

Распределение осцилляторов по энергиям в зависимости от температуры системы показано на рис. 3.9

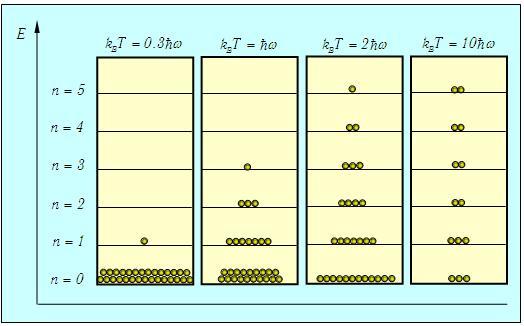
Рис. 3.9. Примерное распределение N = 30 квантовых осцилляторов по энергетическим уровням в зависимости от температуры. Показаны только основной и пять первых возбужденных уровней энергии. При Т = 0 все осцилляторы находятся в основном состоянии. По мере роста температуры становятся доступными все более высокие энергии, и распределение осцилляторов по уровням становится все более равномерным

Для наглядности мы взяли систему из небольшого (N = 30) числа осцилляторов (строго говоря, статистические законы применимы к системам с гораздо большим числом частиц).

Возникает вопрос: каково среднее значение колебательного квантового числа n при некоторой температуре T? Для ответа мы должны подсчитать сумму:

Чтобы сделать это, продифференцируем по q обе части равенства (3.67) для геометрической прогрессии:

Используя (7) при

получаем из (6) выражение для искомого среднего

Теперь легко получить среднюю энергию осциллятора

где функция cth — гиперболический котангенс определена соотношением

На рис. 3.10 сплошной линией изображена средняя энергия квантового осциллятора, измеренная в единицах ħω,

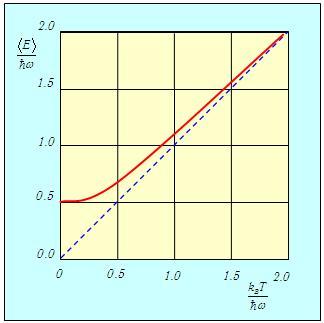
Рис. 3.10. Средняя энергия квантового осциллятора в зависимости от температуры

соответствует результату классической физики. Действительно, энергия

приходящаяся на одну степень свободы, является средним значением как кинетической, так и потенциальной энергий классического осциллятора, так что среднее значение полной энергии как раз равно

Видно, что квантовые поправки важны при низких температурах: при q 14 Гц. Этому соответствуют энергия

Средняя энергия квантового ротатора. Таким образом, привычные для нас комнатные температуры оказываются достаточно низкими с точки зрения возбуждения колебаний молекул. Посмотрим, что происходит с молекулами при температурах Т –27 кг (масса протона), а а_В = 5·10 –11 м — радиус Бора. Получаем тогда

Скорость химических реакций. У химиков есть эмпирическое правило, что при повышении температуры на 10 °С скорость реакции удваивается. Это — всего лишь грубое обобщение, из него есть множество исключений, но все же в целом оно более или менее верно. Объяснение можно и здесь дать на основе распределения Максвелла — Больцмана.

Для протекания многих химических реакций необходимо, чтобы энергия участвующих в них частиц превышала некое пороговое значение, которое мы обозначим Е₀. Чем больше таких частиц, тем выше скорость реакции. Из формул (3.28), (3.29) следует распределение частиц по энергиям. В них надо лишь выразить скорость частицы v через ее кинетическую энергию Е

Распределение (или закон) Максвелла--Больцмана описывает распределение молекул газа по координатам и скоростям при системном воздействии внешнего потенциального поля.

Это распределение выводится из распределения Гиббса ( 1 ) :

где W p – вероятность одного из состояний системы с энергией ε p (полная энергия, состоящая из кинетической и потенциальной, которая присуща частицам). Рассмотрим чаще всего используемые формы распределения Максвелла-Больцмана.

Формы распределения Максвелла-Больцмана

Формула распределения для концентрации частиц

d n ( ν ; x , y , z ) = 4 n 0 π ν ν e r 3 e x p - 1 ν ν e r ν 2 + 2 U ( x , y , z ) m 0 ν 2 d v d V ( 2 ) .

Здесь d n ( v ; x ; y ; z ) – количество частиц, присутствующих в выделенном объеме газа d V . Около точки, имеющей координаты ( x , y , z ) , скорости молекул будут находиться в интервале от v до v + d v . В указанной формуле v v e r есть наиболее вероятная скорость молекул; m 0 – является массой молекулы газа; U ( x , y , z ) – это потенциальная энергия частицы в точке с соответствующими координатами и, наконец, n 0 есть концентрация частиц газа в точке с потенциальной нулевой энергией.

Формула распределения для вероятности импульса и координаты

d w ( p x , p y , p z , x , y , z ) = = A · 1 ( 2 π m 0 k T ) 3 2 e x p - p x 2 + p y 2 + p z 2 2 m 0 k T d p x d p y d p z e x p - U ( x , y , z ) k T d x d y d z ( 3 ) .

В данном выражении d w ( p x , p y , p z , x , y , z ) – переменная, показывающая вероятность нахождения частицы в фазовом объеме d x d y d z d p x d p y d p z возле фазовой точки x , y , z , p x , p y , p z ; U ( x , y , z ) – потенциальная энергия молекулы внешнего поля. В данной формуле распределение Максвелла-Больцмана рассматривается в виде произведения двух вероятностей событий, не зависящих друг от друга: вероятность d w ( p x , p y , p z ) , что молекула имеет импульс ( p x , p y , p z ) и вероятность d w ( x , y , z ) нахождения молекулы в точке ( x , y , z ) . В таком случае выражение ( 3 ) разложится на распределение Максвелла:

d w ( p x , p y , p z ) = 1 2 πm 0 kT 3 2 e x p - p x 2 + p y 2 + p z 2 2 m 0 k T d p x d p y d p z ( 4 ) ,

и распределение Больцмана:

d w x , y , z = A e x p - U ( x , y , z ) k T d x d y d z ( 5 ) .

Таким образом, распределения Максвелла и Больцмана служат составляющими элементами распределения Гиббса. Энергия молекул, движущихся в поле тяжести вверх, получает уменьшение, но в распределении Максвелла-Больцмана по скоростям средняя энергия при этом неизменна. Сохранность средней энергии частиц, когда происходит уменьшение энергии отдельно взятой молекулы, возможно благодаря выбыванию молекул с меньшей энергией из потока при увеличении высоты. Средняя энергия молекул, движущихся вниз, постоянна из-за присоединения к потоку молекул, выбывших из потока, направленного вверх.

Сходство между распределениями Максвелла и Больцмана

Распределения Максвелла и Больцмана обладают общей чертой: и в том и в другом случае законы включают в себя экспоненту, чей показатель в числителе содержит энергию молекулы (кинетическую у Максвелла, потенциальную у Больцмана), а в знаменателе имеют величину - k T , определяющую среднюю энергию теплового движения молекул. Собственно, именно эта схожая черта и дает возможность объединять два распределения в один закон Максвелла-Больцмана.

Рассмотрим практические задачи на распределение Максвелла-Больцмана.

Пусть задан некий газ, имеющий неизменную массу, переводимый из одного равновесного состояния в другое. Необходимо определить, происходит ли изменение в распределении молекул по скоростям: 1 ) положение максимума кривой в распределении Максвелла; 2 ) площадь под этой кривой?

Решение

Составим запись распределения Максвелла по модулю скорости:

d N B d v = 4 π m 0 2 πkT 3 2 exp - m 0 v 2 2 kT v 2 .

При переводе газа из одного равновесного состояния в другое имеет место изменение температуры газа. Таким образом, положение максимума кривой Максвелла изменится.

При этом в случае, когда температура увеличивается, максимум получит сдвиг в сторону больших скоростей, а величина пика (высота по вертикальной оси) уменьшится (рисунок 1 ).

Площадь фигуры, ограниченной кривой и осью скоростей на рисунке 1 , равна единице и останется постоянной при изменении температуры.

Необходимо определить количество молекул кислорода, чьи скорости находятся в пределах от 195 м / с до 205 м / с при температуре Т = 273 К . Масса водорода ( m ) = 0 , 1 к г .

Решение

Заданный условием скоростной интервал невелик, т.е. допустимо применять теорему о среднем, и тогда:

∆ N N ≈ 4 π m O 2 2 πkT 3 2 e x p - m O 2 v 2 2 k T v 2 ∆ v ; ∆ N ≈ 4 πN m O 2 2 πkT 3 2 exp - m O 2 v 2 2 kT v 2 ∆ v ( 2 . 1 ) .

В данном выражении v = 200 м / с , Δ v = 10 м / с , m O 2 μ O 2 = 1 N A → m O 2 = μ O 2 N A , m μ O 2 = N N A → N = m N A μ O 2 .

Подставим полученное в ( 2 . 1 ) :

∆ N ≈ 4 π m N A μ O 2 μ O 2 N A 2 π k T 3 2 e x p - μ O 2 N A v 2 2 k T v 2 ∆ v ( 2 . 2 ) .

Теперь в выражении ( 2 . 2 ) применим конкретные числовые значения и осуществим расчет:

∆ N = 4 · 3 , 14 · 0 , 1 · 6 · 10 23 32 · 10 - 3 32 · 10 - 3 6 · 10 23 2 · 3 , 14 · 1 , 38 · 10 - 23 · 273 3 2 e x p - 32 · 10 - 3 6 · 10 23 · ( 200 ) 2 2 · 1 , 38 · 10 - 23 · 273

Ответ: искомое количество молекул кислорода в заданных условиях равно порядка 2 , 3 ⋅ 1022 .

Закон (или распределение) Максвелла--Больцмана устанавливает распределение молекул газа по координатам и скоростям, если на систему действует внешнее потенциальное поле. Это распределение получают из так называемого распределения Гиббса(1):

где $W_p$- вероятность одного из состояний системы с энергией $_$-- полная энергия, которой обладают частицы (кинетическая плюс потенциальная). Наиболее часто используют следующие формы распределения Максвелла-Больцмана.

Формы распределения Максвелла-Больцмана

Первая для концентрации частиц:

где $dn\left(v;x,y,z\right)$- число частиц, которые находятся в выделенном объеме газа $dV$, вблизи точки с координатами (x,y,z) и скорости этих молекул лежат в интервале от $v\ до\ v+dv;$ $v_$- наиболее вероятная скорость молекул, $m_0$- масса молекулы газа, $U\left(x,y,z\right)$- потенциальная энергия частицы в точке $\left(x,y,z\right)$; $n_0$- концентрация частиц газа в точке, которой потенциальную энергию приняли равной нулю.

Вторая для вероятности импульса и координаты:

где $dw\left(p_x,p_y,p_z,x,y,z\right)-\ \ $вероятность нахождения частицы в фазовом объеме $dxdydzdp_xdp_ydp_z$, около фазовой точки $\left(x,y,z,p_x,p_y,p_z\right)$, $U\left(x,y,z\right)$- потенциальная энергия молекулы во внешнем поле. В виде (3) распределение Максвелла-Больцмана можно рассматривать как произведение двух вероятностей независимых событий. Вероятности $dw\left(p_x,p_y,p_z\right)$того, что молекула обладает импульсом $\left(p_x,p_y,p_z\right)$ и вероятности $dw\left(x,y,z\right)$того, что она находится в точке $\left(x,y,z\right).$ Тогда уравнение (3) распадается на распределение Максвелла:

Итак, распределения Максвелла и Больцмана являются составными частями распределения Гиббса. Энергия молекул, которые движутся в поле тяжести вверх, уменьшается, однако при распределении Максвелла по скоростям средняя энергия при этом постоянна. Сохранение средней энергии частиц, при уменьшении энергии отдельно взятой молекулы осуществляется благодаря выбыванию молекул с меньшей энергией из потока при увеличении высоты. Средняя энергия молекул, которые движутся вниз, не изменяется в результате присоединения к потоку молекул, которые выбыли из потока направленного вверх.

Сходство между распределениями Максвелла и Больцмана

Между распределениями Максвелла и Больцмана имеется существенное сходство: в обоих случаях эти законы содержат экспоненту, показатель которой в числителе содержит энергию молекулы (кинетическую у Максвелла, потенциальную у Больцмана) в знаменателе имеют величину --kT, которая определяет среднюю энергию теплового движения молекул. Это сходство в том числе, и позволяет объединить эти два распределения в один закон Максвела -- Больцмана.

Готовые работы на аналогичную тему

Задание: Некоторый газ с неизменной массой переводят из одного равновесного состояния в другое. Изменяется ли в распределении молекул по скоростям: 1) положение максимума кривой в распределении Максвелла; 2) площадь под этой кривой?

Запишем распределение Максвелла молекул по модулю скорости:

Если газ переводят из одного состояния равновесия в другое, следовательно, изменяется температура газа. Соответственно, положение максимума кривой Максвелла изменится.

Причем, если температура растет, максимум сдвигается в сторону больших скоростей, причем величина пика (высота по вертикальной оси) уменьшается (рис.1).

Площадь фигуры, которая ограничена кривой и осью скоростей на рис 1., равна 1 и не изменяется при изменении температуры.

Задание: Найти число молекул кислорода, скорости которых заключены в пределах от 195 м/c до 205 м/c при температуре T=273 K. Масса водорода (m) 0,1 кг.

Интервал скоростей заданных в условии небольшой, можно использовать теорему о среднем, и тогда мы имеем:

Подставим в (2.2) численные значения, проведем расчет:

Ответ: Количество молекул кислорода при заданных условиях порядка $2,3\cdot ^.$

В равновесном состоянии параметры газа (давле­ние, объем и температура) остаются неизменными, однако микро­состояния — взаимное расположение молекул, их скорости — не­прерывно изменяются. Из-за огромного количества молекул прак­тически нельзя определить значения их скоростей в какой-либо момент, но возможно, считая скорость молекул непрерывной слу­чайной величиной, указать распределение молекул по скоростям.

Выделим отдельную молекулу. Хаотичность движения позволяет, например, для проекции скорости u_x молекулы принять нормальный закон распределения. В этом случае, как показал Дж. К. Максвелл, плотность вероятности записывается следующим образом:

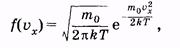(2.28)

где т₀ — масса молекулы, Т — термодинамическая температура газа, k — постоянная Больцмана.

Аналогичные выражения могут быть получены для f(u_у ) и f(u_z).

На основании формулы (2.15) можно записать вероятность то­го, что молекула имеет проекцию скорости, лежащую в интервале от u_x до u_x + du_х:

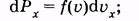
(2.29)

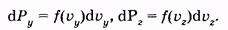(2.30)

аналогично для других осей

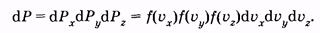(2.31)

Каждое из условий (2.29) и (2.30) отражает независимое событие. Поэтому вероятность того, что молекула имеет скорость, проекции которой одновременно удовлетворяют всем условиям, можно найти по теореме умножения вероятностей [см. (2.6)]:

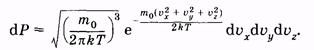(2.32)

Используя (2.28), из (2.31) получаем:

Отметим, что из (2.32) можно получить максвелловскую функ­цию распределения вероятностей абсолютных значений скорости (распределение Максвелла по скоростям):

(2.33)

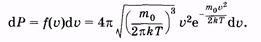(2.34)

и вероятность того, что скорость молекулы имеет значение, лежа­щее в интервале от u до u + du:

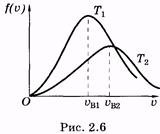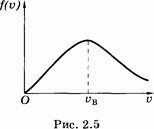
График функции (2.33) изображен на рисунке 2.5. Скорость, соответствующую максимуму кривой Максвелла, называют наивероятнейшей u_в. Ее можно определить, используя условие максимума функции:

или

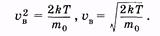(2.35)

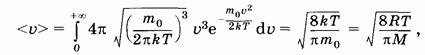(2.36)

Среднюю скорость молекулы (математическое ожидание) мож­но найти по общему правилу [см. (2.20)]. Так как определяется среднее значение скорости, то пределы интегрирования берут от 0 до ¥ (математические подробности опущены):

где М = т₀ N_A — молярная масса газа, R = k N_A— универсальная газовая постоянная, N_A — число Авогадро.

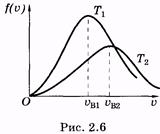
При увеличении температуры максимум кривой Максвелла смещается в сторону больших скоростей и распределение молекул по u видоизменяется (рис. 2.6; Т₁

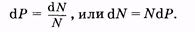(2.37)

Из (2.34) и (2.37) следует, что

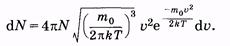(2.38)

Формула (2.38) позволяет определить число молекул, скорости которых лежат в интервале от и_: до i>₂. Для этого нужно проинтег­рировать (2.38):

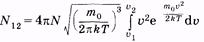(2.39)

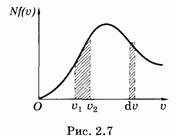
либо графически вычислить площадь криволинейной трапеции в пределах от u₁ до u₂ (рис. 2.7).

Если интервал скоростей du достаточно мал, то число молекул, скорости которых соответствуют этому интервалу, может быть рассчитано приближенно по формуле (2.38) или графически как площадь прямоугольника с основанием du.

Распределение молекул по скоростям подтверждено различны­ми опытами.

Распределение Максвелла можно рассматривать как распреде­ление молекул не только по скоростям, но и по кинетическим энергиям (так как эти понятия взаимосвязаны).

Распределение Больцмана.

Если молекулы находятся в ка­ком-либо внешнем силовом поле, например гравитационном поле Земли, то можно найти распределение по их потенциальным энергиям, т. е. установить концентрацию частиц, обладающих не­которым определенным значением потенциальной энергии.

Распределение частиц по потенциальным энергиям в си­ловых полях — гравитационном, электрическом и др. — называют распределением Больцмана.

Применительно к гравитационному полю это распределение может быть записано в виде зависимости концентрации п моле­кул от высоты h над уровнем Земли или от потенциальной энер­гии молекулы mgh:

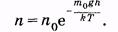(2.40)

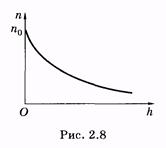
Выражение (2.40) справедливо для частиц идеального газа. Графи­чески эта экспоненциальная зависимость изображена на рис. 2.8.

Такое распределение молекул в поле тяготения Земли можно ка­чественно, в рамках молекулярно-кинетических представлений, объяснить тем, что на молекулы оказывают влияние два противо­положных фактора: гравитационное поле, под действием которого все молекулы притягиваются к Земле, и молекулярно-хаотическое движение, стремящееся равномерно разбросать молекулы по всему возможному объему.

В заключение полезно заметить некоторое сходство экспонен­циальных членов в распределениях Максвелла и Больцмана:

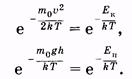
В первом распределении в показателе степени отношение кине­тической энергии молекулы к kT, во втором — отношение потен­циальной энергии к kT.

Распределение Максвелла (распределение молекул газа по скоростям).

В равновесном состоянии параметры газа (давле­ние, объем и температура) остаются неизменными, однако микро­состояния — взаимное расположение молекул, их скорости — не­прерывно изменяются. Из-за огромного количества молекул прак­тически нельзя определить значения их скоростей в какой-либо момент, но возможно, считая скорость молекул непрерывной слу­чайной величиной, указать распределение молекул по скоростям.

Выделим отдельную молекулу. Хаотичность движения позволяет, например, для проекции скорости u_x молекулы принять нормальный закон распределения. В этом случае, как показал Дж. К. Максвелл, плотность вероятности записывается следующим образом:

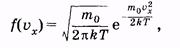(2.28)

где т₀ — масса молекулы, Т — термодинамическая температура газа, k — постоянная Больцмана.

Аналогичные выражения могут быть получены для f(u_у ) и f(u_z).

На основании формулы (2.15) можно записать вероятность то­го, что молекула имеет проекцию скорости, лежащую в интервале от u_x до u_x + du_х:

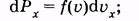
(2.29)

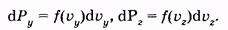(2.30)

аналогично для других осей

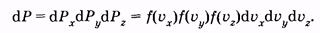(2.31)

Каждое из условий (2.29) и (2.30) отражает независимое событие. Поэтому вероятность того, что молекула имеет скорость, проекции которой одновременно удовлетворяют всем условиям, можно найти по теореме умножения вероятностей [см. (2.6)]:

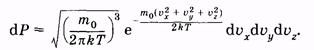(2.32)

Используя (2.28), из (2.31) получаем:

Отметим, что из (2.32) можно получить максвелловскую функ­цию распределения вероятностей абсолютных значений скорости (распределение Максвелла по скоростям):

(2.33)

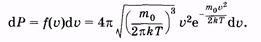(2.34)

и вероятность того, что скорость молекулы имеет значение, лежа­щее в интервале от u до u + du:

График функции (2.33) изображен на рисунке 2.5. Скорость, соответствующую максимуму кривой Максвелла, называют наивероятнейшей u_в. Ее можно определить, используя условие максимума функции:

или

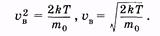(2.35)

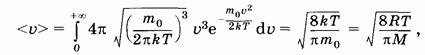(2.36)

Среднюю скорость молекулы (математическое ожидание) мож­но найти по общему правилу [см. (2.20)]. Так как определяется среднее значение скорости, то пределы интегрирования берут от 0 до ¥ (математические подробности опущены):

где М = т₀ N_A — молярная масса газа, R = k N_A— универсальная газовая постоянная, N_A — число Авогадро.

При увеличении температуры максимум кривой Максвелла смещается в сторону больших скоростей и распределение молекул по u видоизменяется (рис. 2.6; Т_{1 2}. Для этого нужно проинтег­рировать (2.38):

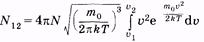(2.39)

либо графически вычислить площадь криволинейной трапеции в пределах от u₁ до u₂ (рис. 2.7).

Если интервал скоростей du достаточно мал, то число молекул, скорости которых соответствуют этому интервалу, может быть рассчитано приближенно по формуле (2.38) или графически как площадь прямоугольника с основанием du.

Распределение молекул по скоростям подтверждено различны­ми опытами.

Распределение Максвелла можно рассматривать как распреде­ление молекул не только по скоростям, но и по кинетическим энергиям (так как эти понятия взаимосвязаны).

Распределение Больцмана.

Если молекулы находятся в ка­ком-либо внешнем силовом поле, например гравитационном поле Земли, то можно найти распределение по их потенциальным энергиям, т. е. установить концентрацию частиц, обладающих не­которым определенным значением потенциальной энергии.

Распределение частиц по потенциальным энергиям в си­ловых полях — гравитационном, электрическом и др. — называют распределением Больцмана.

Применительно к гравитационному полю это распределение может быть записано в виде зависимости концентрации п моле­кул от высоты h над уровнем Земли или от потенциальной энер­гии молекулы mgh:

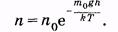(2.40)

Выражение (2.40) справедливо для частиц идеального газа. Графи­чески эта экспоненциальная зависимость изображена на рис. 2.8.

Такое распределение молекул в поле тяготения Земли можно ка­чественно, в рамках молекулярно-кинетических представлений, объяснить тем, что на молекулы оказывают влияние два противо­положных фактора: гравитационное поле, под действием которого все молекулы притягиваются к Земле, и молекулярно-хаотическое движение, стремящееся равномерно разбросать молекулы по всему возможному объему.

В заключение полезно заметить некоторое сходство экспонен­циальных членов в распределениях Максвелла и Больцмана:

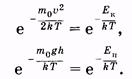
В первом распределении в показателе степени отношение кине­тической энергии молекулы к kT, во втором — отношение потен­циальной энергии к kT.

Распределение, закон Максвелла-Больцмана — распределение молекул газа по координатам и скоростям при наличии произвольного потенциального силового поля; открыто Л. Больцманом в 1871.

Рассмотрим систему частиц, находящуюся в однородном поле. В таком поле каждая молекула идеального газа обладает полной энергией

где ε_kin — кинетическая энергия её поступательного движения, u — потенциальная энергия во внешнем поле, которая зависит от её положения.

Подставим это выражение для энергии в распределение Гиббса для молекулы идеального газа:

где dw — вероятность того, что частица находится в состоянии со значениями координат q и импульсов p , в интервале dp_x dp_y dp_z dV . Имеем:

,

где интеграл состояний равен:

интегрирование ведется по всем возможным значениям переменных. Далее интеграл состояний можно написать в виде:

,

мы находим, что нормированное на единицу распределение Гиббса для молекулы газа при наличии внешнего поля имеет вид:

.

Полученное распределение, характеризующее вероятность того, что молекула имеет данный импульс и находится в данном элементе объема, называется распределением Максвелла-Больцмана.

При рассмотрении распределения Максвелла-Больцмана бросается в глаза важное свойство - его можно представить как произведение двух множителей:

.

Первый множитель есть не что иное, как распределение Максвелла. Оно характеризует распределение вероятностей по импульсам. Второй множитель зависит только лишь от координат частиц и определяется видом её потенциальной энергии. Он характеризует вероятность обнаружения частицы в объеме dV .

Согласно теории вероятности, распределение Максвелла-Больцмана можно рассматривать как произведение вероятностей двух независимых событий — данного значения импульса и данного положения молекулы.

Распределение Максвелла

Распределение Больцмана

Независимость этих двух событий даёт важный результат: данное значение импульса совершенно не зависит от данного положения молекулы и, наоборот, положение молекулы не зависит от её импульса. Это значит, что распределение частиц по импульсам (скоростям) не зависит от поля, другими словами, остается тем же самым от точки к точке пространства, в котором заключен газ. Меняется лишь вероятность обнаружения частицы или, что тоже самое, число частиц.

Читайте также:

  
• Предложение со словом спокойный кратко
  
• Утренний туалет пациента кратко
  
• Отношение к космосу эйнштейновская фкм кратко
  
• Финансовая реформа сперанского кратко
  
• Антон дельвиг интересные факты кратко