Первый замечательный предел доказательство кратко

Обновлено: 02.07.2024

Формулировка и детальное обоснование первого замечательного предела. Приведённых выкладок достаточно для любого экзамена в любом университете.

Есть ещё второй замечательный предел. Помните: это первый шаг в весёлый мир эквивалентных функций, асимптотических переходов и прочих весёлых вещей в матанализе.:)

1. Основная формула

Первый замечательный предел:

Другими словами, чем ближе $x\to 0$, тем ближе значения $\sin x$ и $x$.

2. Вывод формулы

Для вывода формулы первого замечательного предела нам потребуется:

Определение синуса и тангенса на тригонометрической окружности;
Теорема о пределе промежуточной функции — если вы сдаёте устный экзамен, преподаватель может потребовать сформулировать и доказать и эту теорему.

Чтобы доказать существование предела в точке, покажем существование правостороннего предела, левостороннего предела, а затем докажем их равенство.

1. Рассмотрим односторонний предел $\lim\limits_\frac$, т.е. будем приближаться к нулю справа. Следовательно, $x \gt 0$. Более того: поскольку $x\to 0$, достаточно рассмотреть интервал $x\in \left( 0;\frac<\pi > \right)$.

2. Отметим на тригонометрическом круге луч $OM$, соответствующий углу $x$ радиан. Проведём отрезки $AM$ и $MH\bot OA$ так, как показано на рисунке. $N$ — точка пересечения луча $OM$ с вертикальной осью тангенсов.

По определению синуса и тангенса: $\left| MH \right|=\sin x$, $\left| AN \right|=\operatornamex$. Кроме того, дуга $MA$ тоже равна $x$ (если этот момент с дугой непонятен, обязательно повторите, что такое радианная мера угла).

3. Найдём площадь треугольника $AOM$, сектора $AOM$ и треугольника $AON$:

4. Из рисунка видно, что $\Delta OMA\subset \angle AOM$ и $\angle AOM\subset \Delta AON$. Поэтому

Кроме того, поскольку $x\in \left( 0;\frac<\pi > \right)$, можно утверждать, что $\sin x \gt 0$. И последнее двойное неравенство можно переписать так:

Умножим все части неравенства на $\sin x \gt 0$ и получим:

5. Заметим, что $\lim\limits_\cos x=1$ и $\lim\limits_ 1=1$. Следовательно, по теореме о пределе промежуточной функции, имеем:

Но всё это верно лишь для $x \gt 0$.

6. Теперь положим $x \lt 0$. Имеем:

Здесь мы выполнили замену переменной: $t=-x$, что привело к смене левостороннего предела на равносторонний. Но результат тот же.

7. Итак, односторонние пределы существуют и равны 1. Следовательно, сам предел тоже существует и равен 1. Что и требовалось доказать.

3. Следствия из первого замечательного предела

По определению эквивалентных функций, мы можем записать, что $\sin x\sim x$ при $x\to 0$. Кроме того, первый замечательный предел можно переписать в другом виде:

Или в терминах эквивалентности:

\[\begin & \operatornamex\sim x\quad \left( x\to 0 \right) \\ & \arcsin x\sim x\quad \left( x\to 0 \right) \\ & \cos x\sim1-\frac^>>\quad \left( x\to 0 \right) \\ \end\]

Если вы забыли, что такое эквивалентность, обязательно повторите урок про сравнение бесконечно малых.

$\underset<x\to 0> <\mathop<\lim >>\,\frac$

$\underset<x\to 0> <\mathop<\lim >>\,\frac=1$

Доказательство первого замечательного предела

$\underset<x\to 0-0> <\mathop<\lim >>\,\frac; \quad \underset<\mathop<\lim >>\,\frac$

$\underset<x\to 0> Докажем, что каждый из этих пределов равен единице. Тогда и предел <\mathop<\lim >>\,\frac$
также будет равняться единице.

$x\in \left( 0;\ \frac<\pi > Пусть \right)$
и отложим этот угол на тригонометрической окружности (рис. 1).

Этот луч будет пересекать единичную окружность в точке , а вертикальную касательную, проведенную в точке , – в точке . Через точку обозначим проекцию точки на горизонтальную ось косинусов.

Рассмотрим треугольники и круговой сектор . Очевидно следующее двойное неравенство:

Абсцисса точки равна , а ее ордината – (равна высоте ). А тогда

$<<S> _>=\frac\cdot OA\cdot KH=\frac\cdot 1\cdot \sin x=\frac$

Здесь как радиус тригонометрической окружности.

Площадь центрального сектора круга радиуса с центральным углом равна

$<<S> _\ OAK>>=\frac^>x=\frac$

Площадь

$<<S> _>=\frac\cdot OA\cdot AL=\frac\cdot 1\cdot \text\ x=\frac<\text\ x>$

Итак, неравенство (1)перепишется в виде:

$x\in \left( 0;\ \frac<\pi > Так как для \right)$
все части этого неравенства положительны, поэтому его можно записать следующим образом:

После умножения на получаем:

Переходя во всех частях последнего неравенства к пределу при , будем иметь:

$\underset<x\to 0+0> <\mathop<\lim >>\,\frac=1$

$\underset<x\to 0-0> Вычислим теперь <\mathop<\lim >>\,\frac$
:

$\underset<x\to 0-0> <\mathop<\lim >>\,\frac\ \left[ \frac \right]\ \left\| \begin & x=-t \\ & t\to 0+0 \\ \end \right\|=\underset<\mathop<\lim >>\,\frac=\underset<\mathop<\lim >>\,\frac=$

$=\underset<t\to 0+0> <\mathop<\lim >>\,\frac\ \left\| \begin & t=x \\ & x\to 0+0 \\ \end \right\|=\underset<\mathop<\lim >>\,\frac=1$

$\underset<x\to 0-0> То есть <\mathop<\lim >>\,\frac=1$
.

$\underset<x\to 0> А, таким образом, и <\mathop<\lim >>\,\frac=1$
.

Теорема доказана.

Следствия из первого замечательного предела

$\underset<x\to 0> <\mathop<\lim >>\,\frac\ x>=1$

$\underset<x\to 0> <\mathop<\lim >>\,\frac=1$

$\underset<x\to 0> <\mathop<\lim >>\,\frac\ x>=1$

$\underset<x\to 0> <\mathop<\lim >>\,\frac^>>=\frac$

Примеры решения задач

$\underset<x\to 0> <\mathop<\lim >>\,\frac$

$\underset<x\to 0> <\mathop<\lim >>\,\frac\ \left[ \frac=\frac \right]$

$\left[ \frac Таким образом, имеем неопределенность типа \right]$
. Перепишем предел следующим образом:

$\underset <\mathop<\lim >>\,\frac\ \left[ \frac \right]=\underset<\mathop<\lim >>\,\frac<\frac>$

Предел частного равен частному пределов, если последние существуют:

$\underset <\mathop<\lim >>\,\frac\ \left[ \frac \right]=\underset<\mathop<\lim >>\,\frac<\frac>\overset<\mathop<=>>\,\frac<\underset<\mathop<\lim >>\,1><\underset<\mathop<\lim >>\,\frac>$

Предел константы равен этой константе:

$\underset<x\to 0> <\mathop<\lim >>\,1=1$

$\underset<x\to 0> а предел знаменателя есть первый замечательный предел и <\mathop<\lim >>\,\frac=1$
. Тогда, окончательно имеем, что

$\underset<x\to 0> <\mathop<\lim >>\,\frac=\frac=1$

$\underset<x\to 0> <\mathop<\lim >>\,\frac$

$\underset<x\to 0> <\mathop<\lim >>\,\frac\ \left[ \frac>>=\frac \right]$

$\left[ \frac Итак, имеем неопределенность типа \right]$
. Для нахождения предела делаем замену:

$\underset <\mathop<\lim >>\,\frac\ \left[ \frac \right]\ \left\| \begin & \arcsin x=y \\ & x=\sin y \\ & y\to 0 \\ \end \right\|=\underset<\mathop<\lim >>\,\frac$

Получили первый замечательный предел, тогда:

$\underset <\mathop<\lim >>\,\frac\ \left[ \frac \right]\ \left\| \begin & \arcsin x=y \\ & x=\sin y \\ & y\to 0 \\ \end \right\|=\underset<\mathop<\lim >>\,\frac=1$

Предел отношения синуса к его аргументу равняется единице в случае стремления аргумента к 0.

Данная лемма служит основой для вычисления производных тригонометрических функций, которые содержат синус, арксинус, тангенс и арктангенс.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

В записи тождество математического анализа имеет следующий вид:

Доказательство

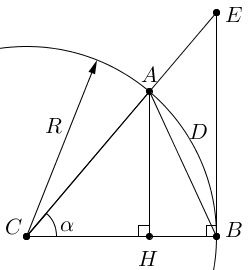
Предположим, что A и B принадлежат окружности с центром в точке С и радиусом, равным R. Отсюда следует, что |CA| = |CB| = R . Из точки А опустим перпендикуляр АН к отрезку СВ, следовательно, АН — это высота треугольника АВС. Далее проведем перпендикуляр ВЕ к стороне ВС до пересечения с прямой СА в точке Е. Обозначим угол между отрезками СА и СВ как α , выраженный в радианах:

Доказательство при 0

Так как длина стороны АВ — это самое краткое расстояние между А и В, то модуль отрезка АВ меньше модуля дуги ADB или:

Из прямоугольного треугольника АВН имеем:

Разделим на число с положительным значением Rα:

Для дальнейшего доказательства необходима лемма.

Верхняя грань множества длин всех ломанных, вписанных в дугу окружности, называется длиной этой дуги.

Согласно этому утверждению:

Подставим в это неравенство:

Выполним умножение на положительное число:

Из (а) и (б) следует, что при 0 :

Доказательство при отрицательных значениях: −π/2 0. Подставим в двойное неравенство (в) и воспользуемся четностью косинуса и нечетностью синуса:

Отсюда следует, что двойное неравенство (в) выполняется для положительных и отрицательных значений 0 \((г)\;\cos\left(\alpha\right)\;

Перейдем в неравенстве (г) к пределу α→0. Используем теорему о промежуточной функции и получим:

Теперь обозначим α буквой x и получим:

Первый замечательный предел доказан.

Примеры решений

Задача 1

Решение

В исходное выражение подставим вместо переменной x значение, равное нулю. Выполнив это, получим:

Далее выполним преобразования, чтобы применить первый замечательный предел. Для этого тангенс представим в виде отношения синуса к косинусу:

Свойства пределов позволяют вынести константу за знак предела, а также произвести замену предела произведения произведением пределов (при существовании последних):

Первый предел последнего выражения является первым замечательным пределом, который равен:

Подставим во второй предел x=0:

Второй замечательный предел

Предел, лежащий в основе нахождения производных показательной функции и логарифма, называется вторым замечательным.

Рассматриваемую лемму можно записать в виде формулы:

В данном случае х — действительное число; e — число Эйлера.

Число Эйлера — это математическая постоянная, трансцендентная величина, то есть число, которое не может являться корнем полинома с целыми коэффициентами. e≈2,7182818284.

Доказательство

Чтобы доказать указанное утверждение, будем применять факт, что последовательность

строго возрастает и ее конечный предел равен величине е:

Для начала рассмотрим правый предел:

Чтобы он существовал, необходимо существование такой окрестности +∞, где функция является определенной и имеет вид:

В конкретном случае f(x) определена при x>0. Можно выбрать любую окрестность. Для удобства примем x≥1.

Пусть n(x) — это функция, обозначающая целую часть числа x, к примеру: n(1)=1, n(1,2)=1, n(2,02)=2, n(3)=3. Указанная функция неубывающая.

Рассмотрим сложную функцию:

Приведем доказательство того, что при условии x→+∞ она имеет предел, равный числу Эйлера:

Так как последовательность

строго возрастающая, а n(x) — неубывающая, сложная функция g(x) также не убывает.

В этом случае по теореме о пределе монотонной функции данная сложная функция обладает конечным, либо бесконечным пределом при условии x→+∞:

Покажем, что А=e с применением определения предела функции по Гейне. Согласно ему: если g(x) имеет предел при x→x₀:

В этой ситуации для любой последовательности  , сходящейся к x₀, последовательность  сходится к А:

Возьмем последовательность y_n=n, которая сходится к +∞, тогда:

Поскольку последовательность  совпадает с  :

Поэтому предел данной последовательности равен:

В результате приходим к равенству А=е:

Подставим x=t+1. Отметим, что x(n)=n(t+1)=n(t)+1. Заменим переменную t на x и получим:

Далее воспользуемся условием n(x)≤x≤n(x)+1, значит:

Используем арифметические свойства предела функции и пределы (а) и (б):

Применим к (в) теорему о промежуточной функции и получим:

Далее рассмотрим левый предел:

Пусть x≤−2. Произведем подстановку x=−y и получим y≥2. При x→−∞, y→+∞.

Применим арифметические свойства предела функции:

Так как и справа, и слева существуют равные пределы, то имеет место двусторонний предел:

Второй замечательный предел доказан.

Примеры решений

Задача 1

Решение

Выражение 7−6x стремится к 1 при условии, что x→1, то есть:

Для показателя степени x/3x-3 получаем:

Таким образом, в данном случае имеет место неопределенность вида 1 в степени бесконечности. Ее возможно раскрыть с применением второго замечательного предела.

Сначала отметим, что в формуле:

x стремится к бесконечности, а в формуле:

t стремится к нулю.

В данном примере x стремится к единице, поэтому для удобства введем еще одну переменную, стремящуюся либо к бесконечности, либо к нулю, чтобы воспользоваться одной из приведенных выше формул.

Пусть новая переменная y равна разности x−1. Поскольку x стремится к 1, то x−1 стремится к нулю, то есть y→0.

Подставим x=y+1 при y→0:

Основание 1+t соответствует выражению в основании примера 1+(−6y). Исходя из формулы, показатель степени должен иметь вид 1/t, следовательно, необходимо привести показатель степени в примере к соотношению 1/−6y. Для этого умножим его на данную дробь. Компенсируем это действие с помощью дополнительного умножения на обратную дробь, то есть фактически на −6y:

Рассмотрим функцию y = , аргумент x (как всегда в математическом анализе) выражается в радианах. При x = 0 функция не определена.

Теорема. = 1 (первый замечательный предел).

Доказательство

1) Пусть a – положительный острый угол, докажем = 1. Предварительно докажем, что sina = 0 и cosa = 1.

Рассмотрим окружность радиуса R (рис. 1.12), OA = OC = R, тогда длина дуги АС равна: R×a, АВ = R×sina. Так как |AB| 2 , то на основании теорем о пределах получим:

cosa = (1 – 2sin 2 ) = 1 – 2×0 = 1.

Из рис. 1.12 видим, что

S_D_OAC 2 sina, S_{секторOAC} = R 2 ×a, S_D_ODC = R 2 tga.

Подставляя последние выражения в неравенства (*), находим:

R 2 sina 2 ×a 2 tga.

Деля все части неравенства (**) на положительное число R 2 sina, получим:

1 > cosa (***)

Применяя к неравенству (***) теорему о сжатой переменной при a ® 0 получим:

= 1 (ведь cosa = 1).

2) Пусть x 0, = = =1.

Итак, доказано, что = 1, , а потому .

С помощью этого предела находятся многие другие пределы, содержащие тригонометрические функции.

Срочно?
Закажи у профессионала, через форму заявки
8 (800) 100-77-13 с 7.00 до 22.00

Материал представлен на сайте исключительно в ознакомительных целях.
Все права принадлежат авторам этих материалов.

Читайте также: