Момент силы и момент инерции кратко
Обновлено: 07.07.2024
Основная задача динамики вращательного движения - определение угловых координат точек вращающегося тела в любой момент времени по известным начальным угловым координатам, угловым скоростям и по заданным моментам внешних сил, действующих на тело.
Твёрдое тело – тело, все части которого неизменно сохраняют своё расположение; конфигурация частей твёрдого тела не изменяется даже при действии внешних сил. В частности, неизменными остаются расстояния между его частями.
Это идеальное представление об абсолютно твёрдом теле (см. определение в § I.1.1). В реальности же все существующие в природе твёрдые тела деформируются под действием сил, однако, деформации многих твёрдых тел очень малы относительно прикладываемых к ним сил и поэтому мы можем смело пользоваться упрощённой моделью абсолютно твёрдого тела.
Абсолютно твёрдое тело, имеющее закреплённую ось вращения, без воздействия моментов внешних сил не изменяет угловой скорости вращательного движения. При этом в инерциальной системе отсчёта тело либо покоится ( ), либо вращается с постоянной угловой скоростью, одинаковой для всех точек тела и .
Вращение тела вокруг оси под действием одной силы может быть остановлено действием второй силы (рис.33). Если две силы и по отдельности вызывают вращение тела в противоположных направлениях, то при их одновременном действии тело находится в равновесии, если выполняется условие: ;
где и - радиус-вектор (плечо силы – кратчайшее расстояние от оси вращения до линии действия силы). Из рисунка 35следует, что а .
Моментом силы относительно неподвижной точки называется физическая величина, определяемая векторным произведением радиус-вектора , проведённого из точки в точку приложения силы (на рис. 33, это точки и ), на силу :
Момент силы является псевдовектором, его направление совпадает с направлением поступательного движения правого винта при его вращении от радиус-вектора к силе .
Модуль момента силы:
За единицу вращающего момента в СИ принимается момент силы в 1Н, линия действия которой находится на расстоянии 1 м от оси вращения. Эту единицу называют ньютон – метром (Н·м).
Суммарный момент нескольких сил, действующих на тело, равен алгебраической сумме моментов всех сил относительно данной оси:
Если моментам сил, вызывающим вращение тела вокруг оси по часовой стрелке, приписать положительный знак, а моментам сил, вызывающим вращение против часовой стрелки, - отрицательный знак, то условие равновесия тела, имеющего ось вращения, можно сформулировать в виде правила моментов.
Правило моментов: тело, имеющее неподвижную ось вращения, находится в равновесии, если алгебраическая сумма моментов всех приложенных к телу сил относительно этой оси равна нулю:
Общее условие равновесия тел: тело находится в равновесии, если равны нулю геометрическая сумма векторов всех приложенных к нему сил и алгебраическая сумма моментов этих сил относительно оси вращения.
Моментом инерции материальной точки относительно данной оси называется физическая величина , равная произведению массы точки на квадрат её расстояния от оси:
Рассматривая твёрдое тело как систему неизменно соединённых между собой материальных точек с массами , расположенных на расстояниях от оси вращения (рис.34). Каждая из этих точек имеет свой момент инерции ; сумму моментов инерции всех точек, составляющих данное тело, будем называть - моментом инерции тела относительно оси вращения: ; или
Исходя из формулы (I.100), можно дать следующее определение момента инерции тела.
Моментом инерции тела (механической системы) относительно неподвижной оси называется физическая величина , равная сумме произведений масс всех материальных точек тела (системы) на квадраты их расстояний до оси.
В случае непрерывного распределения масс эта сумма сводится к интегралу вида:
где - масса малого элемента объёма тела. Пределы интегрирования определяются формой и размерами тела.
Из формул (I.100) и (I.101) следует, что момент инерции тела зависит от:
§ распределения массы относительно данной оси.
Момент инерции является мерой инертности тела при вращательном движении. Он играет такую же роль, что и масса при описании поступательного движения тела. Но если масса данного тела считается величиной постоянной, то момент инерции данного тела зависит от положения оси вращения. Кроме того, на момент инерции влияют форма и размеры тела.
Согласно теореме Гюйгенса – Штейнера (теореме о переносе осей инерции): момент инерции тела (рис. 35) относительно произвольной оси равен сумме момента инерции этого тела относительно оси, проходящей через центр инерции тела (центр масс) параллельно рассматриваемой оси, и произведения массы тела на квадрат расстояния между осями:
Из теоремы Гюйгенса – Штейнера, следует, что:
q параллельное смещение оси вращения, проходящей через центр масс, приводит к увеличению момента инерции данного тела;
q момент инерции тела минимален, если ось вращения проходит через центр масс: ;
q оси, проходящие через точку и через центр масс (точку ), должны быть параллельны.
Формула (I.101), позволяет рассчитать моменты инерции тел простейшей формы относительно некоторых осей.
1. Момент инерции однородного прямого тонкого цилиндрического стержня длины и массы относительно оси проходящей через его середину и перпендикулярной к его длине:
2. Момент инерции однородного сплошного цилиндра (или диска) радиуса и массы относительно оси симметрии перпендикулярной к его плоскости и проходящей через его центр:
3. Момент инерции цилиндра радиуса , массы и высоты относительно оси, перпендикулярной к его высоте и проходящей через её середину:
4. Момент инерции шара (тонкостенной сферы) радиуса и массы относительно его диаметра (или оси проходящей через центр сферы):
5. Момент инерции стержня длины и массы , относительно оси проходящей через один из его концов и перпендикулярной к его длине:
6. Момент инерции полого тонкостенного цилиндра радиуса и массы , относительно оси цилиндра:
При изучении закономерностей поступательного движения твердого тела было установлено, что основным уравнением, описывающим данный тип движения, является второй закон Ньютона. Установлено: характеристики движения тела зависят как от выбора систем отсчета, так и от интенсивности взаимодействия тела с окружающими его телами (в инерциальных системах отсчета характеристики движения определяются только взаимодействием).
Для измерения интенсивности взаимодействий использовали величину, называемую силой, а инертность при поступательных движениях оценивали массой тела. Оказывается, для вращательных движений результат взаимодействия зависит как от силы и ее направления, так и от точки приложения. В сказанном нетрудно убедиться на следующем примере: если два человека прикладывают одинаковые усилия перпендикулярно двери, то она будет вращаться в направлении той силы, точка приложения которой наиболее удалена от оси вращения. Для вращательных движений мерой взаимодействия является момент силы.
Рассмотрим понятие момента силы относительно некоторой точки . Построим вектор силы и ее линию действия (пунктирная линия на рис. 4.1.а). Проведем перпендикуляр из точки к линии действия силы, величину которого обозначим и назовем его плечом силы.
Величиной момента силы относительно точки называется произведение величины силы на ее плечо, т.е.:
Единицы измерения момента силы в системе СИ – .
Для того, чтобы в дальнейшем интенсивно использовать аппарат векторной алгебры, введем понятие вектора момента силы.
Проведем из точки в точку приложения силы радиус–вектор , и назовем его радиус–вектор силы. Из рис. 4.1.а видно, что:
С учетом соотношения (4.2), равенство (4.1) примет вид:
Последнее соотношение позволяет записать для вектора момента силы следующее равенство:
Вращаем буравчик от вектора к вектору , тогда его поступательное движение указывает на направление вектора момента силы . Важно помнить, что направление вектора всегда перпендикулярно плоскости, в которой расположены векторы и , или и .
Если радиус–вектор силы задан в декартовой системе координат соотношением , а сам вектор силы как – , ( единичные вектора прямоугольной декартовой системы координат) то вектор момента силы находится следующим образом:
Кроме вектора момента силы, в динамике твердого тела часто пользуются проекцией этого вектора на некоторую ось , иначе эту величину называют моментом силы относительно оси. Выберем точку и построим векторы и так, как показано на рис. 4.2.
Из точки построим вектор момента силы , относительно этой точки. Выберем произвольно ось (см. рис. 4.2), и проведем перпендикуляр из конца вектора на ось , получим составляющую вектора по оси. Кроме того, построим плечо силы и отрезок, перпендикулярный оси и линии действия силы , величину которого обозначим и назовем плечом силы относительно оси .
Из рис. 4.2 видно, что длина составляющей связана с длиной вектора следующим соотношением , но . Подставляя из последнего равенства в предыдущее, имеем следующее соотношение для проекции момента силы на ось :
Таким образом, величина проекции момента силы на ось (момент силы относительно оси ) равна произведению величины силы на ее плечо относительно оси .
Важно помнить, что последнее соотношение позволяет находить только величину проекции вектора на ось . Знак проекции определяется по рисунку. Кроме того, если вектор силы параллелен оси , или ось лежит в плоскости векторов и , то проекция вектора на эту ось равна нулю.
Важной характеристикой динамики твердого тела является момент импульса. Введем понятие момента импульса материальной точки относительно заданной точки .
Рассуждая также, как делали при построении момента вектора силы, построим вектор момента импульса (см. рис. 4.3.а), где перпендикуляр, опущенный из точки на линию действия вектора импульса есть плечо этого вектора относительно точки .

Вектор момента импульса материальной точки относительно заданной точки равен векторному произведению радиус–вектора, проведенного из точки в точку приложения импульса на вектор импульса, т.е.:
Единицы измерения вектора момента импульса в системе СИ – .
Важно помнить, что направление вектора всегда перпендикулярно плоскости, в которой расположены векторы и , или и .
Если радиус–вектор импульса задан в декартовой системе координат соотношением , а сам вектор импульса как– , то вектор момента импульса находится из соотношения:
Величина вектора момента импульса материальной точки равна произведению величины вектора импульса на его плечо, т.е.:
Величина проекции момента импульса на ось (момент импульса относительно оси ) равна произведению величины импульса материальной точки на его плечо относительно оси.
Важно помнить, что последнее определение позволяет находить только величину проекции вектора на ось . Кроме того, если вектор импульса параллелен оси , или ось лежит в плоскости векторов и , то проекция вектора на эту ось равна нулю.
Введем понятие вектора момента импульса твердого тела. Момент импульса, как и большинство физических величин, является величиной аддитивной. Возьмем твердое тело и разобьем его на бесконечно малые части, такие, что размер части пренебрежимо мал по сравнению с размерами твердого тела. Определим момент импульса каждой части ( ). Момент импульса всего тела равен при этом сумме моментов всех его частей, т.е.:
Таким образом мы ввели понятие величины, которая является аналогом вектора импульса твердого тела для поступательного движения.
Для поступательных движений тел мерой инертности является масса. Способность тел сохранять состояние равномерного вращения в отсутствии моментов внешних сил зависит не только от их массы, но и от конфигурации этих тел. Очевидно, что из двух маховиков с равными массами, маховик, имеющий больший радиус, обладает большей способностью сохранять равномерное вращательное движение. Для этих целей вводится понятие момента инерции.
Введем в начале понятие момента инерции материальной точки относительно заданной точки и оси .Выберем материальную точку массой . Проведем из заданной точки радиус–вектор в данную точку, расстояние от нее до оси обозначим через (см. рис. 3.4).
Моментом инерции материальной точки относительно выбранной точки называется величина, равная произведению массы материальной точки на квадрат расстояния от нее до точки , т.е.
Моментом инерции материальной точки относительно оси называется величина, равная произведению массы точки на квадрат расстояния от материальной точки до оси , т.е.
Единицы измерения момента инерции в системе СИ – .
Введем понятия момента инерции твердого тела, используем для этого свойство аддитивности этой величины. Разобьем твердое тело на бесконечно малых частей, найдем момент инерции каждой части относительно точки ( ).
Момент инерции твердого тела относительно точки равен сумме моментов инерции бесконечно малых его частей, т.е.:
Момент инерции твердого тела относительно оси равен сумме произведений масс бесконечно малых частей на квадрат расстояний от данных частей до оси , т.е.:
Чем точнее мы хотим оценить момент инерции тела с помощью указанных сумм, тем большее число бесконечно малых частей мы должны брать, поэтому точные значения моментов инерций твердого тела относительно точки и оси будут совпадать с пределами от правых частей равенств (4.10) и (4.11) при условии, что , т.е.:
Вопросы для самоконтроля
1. Какие характеристики вращательного движения аналогичны вектору силы и вектору импульса при поступательном движении?
2. Что называется плечом вектора силы относительно точки?
3. Что называется плечом вектора силы относительно оси?
4. Дайте определение вектора момента силы относительно точки. Как вычисляется проекция момента силы на ось (величина момента силы относительно оси)?
5. В каких единицах в системе СИ измеряется момент силы?
6. Как определяется направление вектора момента силы? В каких случаях его величина равна нулю?
7. Зная, что радиус-вектор силы задан выражением , и сам вектор силы как – , запишите соотношение, по которому можно рассчитать вектор момента силы.
8. Что называется плечом вектора импульса относительно точки?
9. Что называется плечом вектора импульса относительно оси?
10. Дайте определение вектора момента импульса материальной точки относительно заданной точки. Как вычисляется проекция момента импульса материальной точки на ось (величина момента импульса относительно оси)?
11. В каких единицах в системе СИ измеряется момент силы?
12. Как определяется направление вектора момента импульса? В каких случаях его величина равна нулю?
13. Зная, что радиус-вектор импульса задан как – , и сам вектор силы как – , запишите соотношение, по которому можно рассчитать вектор момента импульса материальной точки.
14. Что понимается под свойством аддитивности?
15. Дайте определение вектора момента импульса твердого тела. Как вычисляется величина проекции момента импульса тела на ось (момент импульса относительно оси)?
16. В каких единицах в системе СИ измеряется момент импульса?
17. Что называется моментом инерции материальной точки относительно некоторой точки?
18. Дайте определение момента инерции материальной точки относительно заданной оси.
19. Сформулируйте определение момента инерции твердого тела относительно точки.
20. Как находится момент инерции тела относительно оси?
Динамика твердого тела
При изучении закономерностей поступательного движения твердого тела было установлено, что основным уравнением, описывающим данный тип движения, является второй закон Ньютона. Установлено: характеристики движения тела зависят как от выбора систем отсчета, так и от интенсивности взаимодействия тела с окружающими его телами (в инерциальных системах отсчета характеристики движения определяются только взаимодействием).
Для измерения интенсивности взаимодействий использовали величину, называемую силой, а инертность при поступательных движениях оценивали массой тела. Оказывается, для вращательных движений результат взаимодействия зависит как от силы и ее направления, так и от точки приложения. В сказанном нетрудно убедиться на следующем примере: если два человека прикладывают одинаковые усилия перпендикулярно двери, то она будет вращаться в направлении той силы, точка приложения которой наиболее удалена от оси вращения. Для вращательных движений мерой взаимодействия является момент силы.
Рассмотрим понятие момента силы относительно некоторой точки . Построим вектор силы и ее линию действия (пунктирная линия на рис. 4.1.а). Проведем перпендикуляр из точки к линии действия силы, величину которого обозначим и назовем его плечом силы.
Величиной момента силы относительно точки называется произведение величины силы на ее плечо, т.е.:
Единицы измерения момента силы в системе СИ – .
Для того, чтобы в дальнейшем интенсивно использовать аппарат векторной алгебры, введем понятие вектора момента силы.
Проведем из точки в точку приложения силы радиус–вектор , и назовем его радиус–вектор силы. Из рис. 4.1.а видно, что:
С учетом соотношения (4.2), равенство (4.1) примет вид:
Последнее соотношение позволяет записать для вектора момента силы следующее равенство:
Вращаем буравчик от вектора к вектору , тогда его поступательное движение указывает на направление вектора момента силы . Важно помнить, что направление вектора всегда перпендикулярно плоскости, в которой расположены векторы и , или и .
Если радиус–вектор силы задан в декартовой системе координат соотношением , а сам вектор силы как – , ( единичные вектора прямоугольной декартовой системы координат) то вектор момента силы находится следующим образом:
Кроме вектора момента силы, в динамике твердого тела часто пользуются проекцией этого вектора на некоторую ось , иначе эту величину называют моментом силы относительно оси. Выберем точку и построим векторы и так, как показано на рис. 4.2.
Из точки построим вектор момента силы , относительно этой точки. Выберем произвольно ось (см. рис. 4.2), и проведем перпендикуляр из конца вектора на ось , получим составляющую вектора по оси. Кроме того, построим плечо силы и отрезок, перпендикулярный оси и линии действия силы , величину которого обозначим и назовем плечом силы относительно оси .
Из рис. 4.2 видно, что длина составляющей связана с длиной вектора следующим соотношением , но . Подставляя из последнего равенства в предыдущее, имеем следующее соотношение для проекции момента силы на ось :
Таким образом, величина проекции момента силы на ось (момент силы относительно оси ) равна произведению величины силы на ее плечо относительно оси .
Важно помнить, что последнее соотношение позволяет находить только величину проекции вектора на ось . Знак проекции определяется по рисунку. Кроме того, если вектор силы параллелен оси , или ось лежит в плоскости векторов и , то проекция вектора на эту ось равна нулю.
Важной характеристикой динамики твердого тела является момент импульса. Введем понятие момента импульса материальной точки относительно заданной точки .
Рассуждая также, как делали при построении момента вектора силы, построим вектор момента импульса (см. рис. 4.3.а), где перпендикуляр, опущенный из точки на линию действия вектора импульса есть плечо этого вектора относительно точки .
Вектор момента импульса материальной точки относительно заданной точки равен векторному произведению радиус–вектора, проведенного из точки в точку приложения импульса на вектор импульса, т.е.:
Единицы измерения вектора момента импульса в системе СИ – .
Важно помнить, что направление вектора всегда перпендикулярно плоскости, в которой расположены векторы и , или и .
Если радиус–вектор импульса задан в декартовой системе координат соотношением , а сам вектор импульса как– , то вектор момента импульса находится из соотношения:
Величина вектора момента импульса материальной точки равна произведению величины вектора импульса на его плечо, т.е.:
Величина проекции момента импульса на ось (момент импульса относительно оси ) равна произведению величины импульса материальной точки на его плечо относительно оси.
Важно помнить, что последнее определение позволяет находить только величину проекции вектора на ось . Кроме того, если вектор импульса параллелен оси , или ось лежит в плоскости векторов и , то проекция вектора на эту ось равна нулю.
Введем понятие вектора момента импульса твердого тела. Момент импульса, как и большинство физических величин, является величиной аддитивной. Возьмем твердое тело и разобьем его на бесконечно малые части, такие, что размер части пренебрежимо мал по сравнению с размерами твердого тела. Определим момент импульса каждой части ( ). Момент импульса всего тела равен при этом сумме моментов всех его частей, т.е.:
Таким образом мы ввели понятие величины, которая является аналогом вектора импульса твердого тела для поступательного движения.
Для поступательных движений тел мерой инертности является масса. Способность тел сохранять состояние равномерного вращения в отсутствии моментов внешних сил зависит не только от их массы, но и от конфигурации этих тел. Очевидно, что из двух маховиков с равными массами, маховик, имеющий больший радиус, обладает большей способностью сохранять равномерное вращательное движение. Для этих целей вводится понятие момента инерции.
Введем в начале понятие момента инерции материальной точки относительно заданной точки и оси .Выберем материальную точку массой . Проведем из заданной точки радиус–вектор в данную точку, расстояние от нее до оси обозначим через (см. рис. 3.4).
Моментом инерции материальной точки относительно выбранной точки называется величина, равная произведению массы материальной точки на квадрат расстояния от нее до точки , т.е.
Моментом инерции материальной точки относительно оси называется величина, равная произведению массы точки на квадрат расстояния от материальной точки до оси , т.е.
Единицы измерения момента инерции в системе СИ – .
Введем понятия момента инерции твердого тела, используем для этого свойство аддитивности этой величины. Разобьем твердое тело на бесконечно малых частей, найдем момент инерции каждой части относительно точки ( ).
Момент инерции твердого тела относительно точки равен сумме моментов инерции бесконечно малых его частей, т.е.:
Момент инерции твердого тела относительно оси равен сумме произведений масс бесконечно малых частей на квадрат расстояний от данных частей до оси , т.е.:
Чем точнее мы хотим оценить момент инерции тела с помощью указанных сумм, тем большее число бесконечно малых частей мы должны брать, поэтому точные значения моментов инерций твердого тела относительно точки и оси будут совпадать с пределами от правых частей равенств (4.10) и (4.11) при условии, что , т.е.:
Вопросы для самоконтроля
1. Какие характеристики вращательного движения аналогичны вектору силы и вектору импульса при поступательном движении?
2. Что называется плечом вектора силы относительно точки?
3. Что называется плечом вектора силы относительно оси?
4. Дайте определение вектора момента силы относительно точки. Как вычисляется проекция момента силы на ось (величина момента силы относительно оси)?
5. В каких единицах в системе СИ измеряется момент силы?
6. Как определяется направление вектора момента силы? В каких случаях его величина равна нулю?
7. Зная, что радиус-вектор силы задан выражением , и сам вектор силы как – , запишите соотношение, по которому можно рассчитать вектор момента силы.
8. Что называется плечом вектора импульса относительно точки?
9. Что называется плечом вектора импульса относительно оси?
10. Дайте определение вектора момента импульса материальной точки относительно заданной точки. Как вычисляется проекция момента импульса материальной точки на ось (величина момента импульса относительно оси)?
11. В каких единицах в системе СИ измеряется момент силы?
12. Как определяется направление вектора момента импульса? В каких случаях его величина равна нулю?
13. Зная, что радиус-вектор импульса задан как – , и сам вектор силы как – , запишите соотношение, по которому можно рассчитать вектор момента импульса материальной точки.
14. Что понимается под свойством аддитивности?
15. Дайте определение вектора момента импульса твердого тела. Как вычисляется величина проекции момента импульса тела на ось (момент импульса относительно оси)?
16. В каких единицах в системе СИ измеряется момент импульса?
17. Что называется моментом инерции материальной точки относительно некоторой точки?
18. Дайте определение момента инерции материальной точки относительно заданной оси.
19. Сформулируйте определение момента инерции твердого тела относительно точки.

Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Что такое инерция
Согласно определению инерция в физике – это способность тел сохранять состояние покоя или движения в отсутствие действия внешних сил.
Определение момента инерции
Из школьного курса известно, что масса – мера инертности тела. Если мы толкнем две тележки разной массы, то остановить сложнее будет ту, которая тяжелее. То есть чем больше масса, тем большее внешнее воздействие необходимо, чтобы изменить движение тела. Рассмотренное относится к поступательному движению, когда тележка из примера движется по прямой.

По аналогии с массой и поступательным движением момент инерции – это мера инертности тела при вращательном движении вокруг оси.
Момент инерции – скалярная физическая величина, мера инертности тела при вращении вокруг оси. Обозначается буквой J и в системе СИ измеряется в килограммах, умноженных на квадратный метр.
Как посчитать момент инерции? Есть общая формула, по которой в физике вычисляется момент инерции любого тела. Если тело разбить на бесконечно малые кусочки массой dm, то момент инерции будет равен сумме произведений этих элементарных масс на квадрат расстояния до оси вращения.

Это общая формула для момента инерции в физике. Для материальной точки массы m, вращающейся вокруг оси на расстоянии r от нее, данная формула принимает вид:

Теорема Штейнера
От чего зависит момент инерции? От массы, положения оси вращения, формы и размеров тела.
Теорема Гюйгенса-Штейнера – очень важная теорема, которую часто используют при решении задач.
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Теорема Гюйгенса-Штейнера гласит:
Момент инерции тела относительно произвольной оси равняется сумме момента инерции тела относительно оси, проходящей через центр масс параллельно произвольной оси и произведения массы тела на квадрат расстояния между осями.

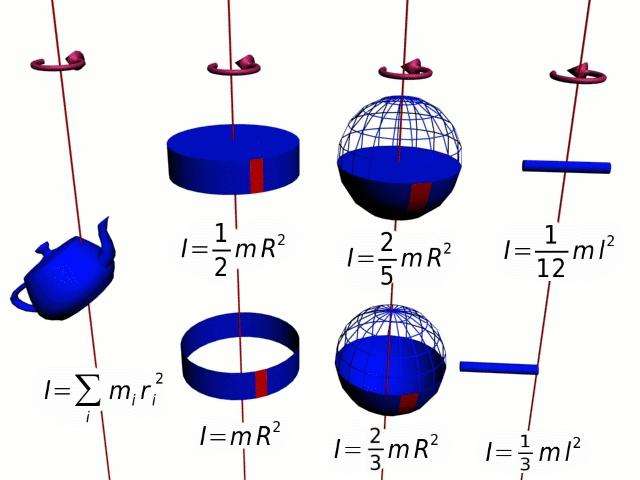
Для тех, кто не хочет постоянно интегрировать при решении задач на нахождение момента инерции, приведем рисунок с указанием моментов инерции некоторых однородных тел, которые часто встречаются в задачах:

Пример решения задачи на нахождение момента инерции
Рассмотрим два примера. Первая задача – на нахождение момента инерции. Вторая задача – на использование теоремы Гюйгенса-Штейнера.
Задача 1. Найти момент инерции однородного диска массы m и радиуса R. Ось вращения проходит через центр диска.
Разобьем диск на бесконечно тонкие кольца, радиус которых меняется от 0 до R и рассмотрим одно такое кольцо. Пусть его радиус – r, а масса – dm. Тогда момент инерции кольца:

Массу кольца можно представить в виде:

Здесь dz – высота кольца. Подставим массу в формулу для момента инерции и проинтегрируем:

В итоге получилась формула для момента инерции абсолютного тонкого диска или цилиндра.
Задача 2. Пусть опять есть диск массы m и радиуса R. Теперь нужно найти момент инерции диска относительно оси, проходящей через середину одного из его радиусов.
Момент инерции диска относительно оси, проходящей через центр масс, известен из предыдущей задачи. Применим теорему Штейнера и найдем:

Кстати, в нашем блоге Вы можете найти и другие полезные материалы по физике и решению задач.
Надеемся, что Вы найдете в статье что-то полезное для себя. Если в процессе расчета тензора инерции возникают трудности, не забывайте о студенческом сервисе. Наши специалисты проконсультируют по любому вопросу и помогут решить задачу в считанные минуты.
Если линейное перемещение тел описывают в классической механике с помощью законов Ньютона, то характеристики движения механических систем по круговым траекториям вычисляют с помощью специального выражения, которое называется уравнением моментов. О каких моментах идет речь и в чем заключается смысл этого уравнения? Эти и другие вопросы раскрываются в статье.
Момент силы
Вам будет интересно: Эмфатические конструкции в английском языке: правила составления, особенности перевода
Рисунок, поясняющий это выражение, приведен ниже.
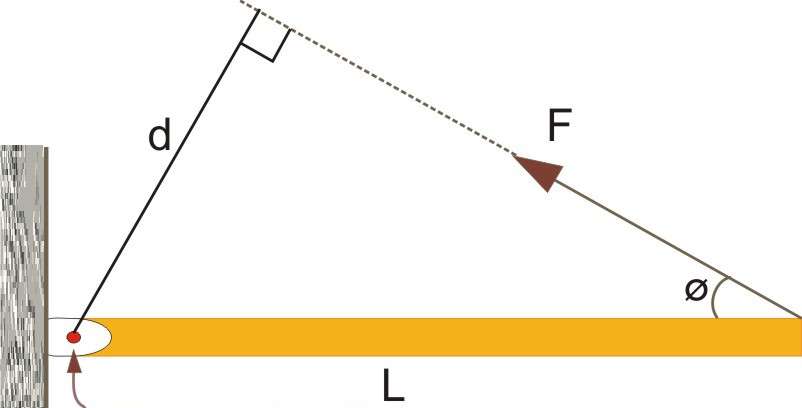
Здесь видно, что сила F¯ направлена к вектору L¯ под углом Φ. Сам же вектор L¯ полагается направленным от оси вращения (указана стрелкой) к точке приложения F¯.
Вам будет интересно: Что такое дендриты и дендритные шипики
Приведенная выше формула представляет собой произведение двух векторов, поэтому величина M¯ также является направленной. Куда будет повернут момент силы M¯? Это можно определить по правилу правой руки (четыре пальца направлены вдоль траектории от конца вектора L¯ к концу F¯, а отставленный палец большой показывает направление M¯).
На рисунке выше выражение для момента силы в скалярном виде примет форму:
Если внимательно всмотреться в рисунок, то можно увидеть, что L*sin(Φ) = d, тогда имеем формулу:
Величина d является важной характеристикой при вычислении момента силы, поскольку она отражает эффективность приложенной F к системе. Эту величину принято называть рычагом силы.
Физический смысл M заключается в способности силы совершить вращение системы. Эту способность может ощутить на себе каждый, если будет открывать дверь за ручку, толкая ее около петель, или же попробует открутить гайку коротким и длинным ключом.
Равновесие системы
Понятие о моменте силы оказывается очень полезным, когда рассматривают равновесие системы, на которую действуют несколько сил, и которая имеет ось или точку вращения. В таких случаях применяют формулу:
То есть система будет находиться в равновесии, если сумма всех моментов сил, приложенных к ней, нулевая. Заметим, что в этой формуле присутствует знак вектора над моментом, то есть при решении следует не забывать учитывать знак этой величины. Общепринятым правилом считается, что действующая сила, которая вращает систему против часовой стрелки, создает положительный Mi¯.

Ярким примером задач рассматриваемого типа являются проблемы с равновесием рычагов Архимеда.
Момент импульса
Это еще одна важная характеристика движения по окружности. В физике ее описывают произведением количества движения на рычаг. Уравнение момента импульса имеет такой вид:
Здесь p¯ - вектор импульса, r¯ - вектор, соединяющий вращающуюся материальную точку с осью.
Поясняющий это выражение рисунок приведен ниже.
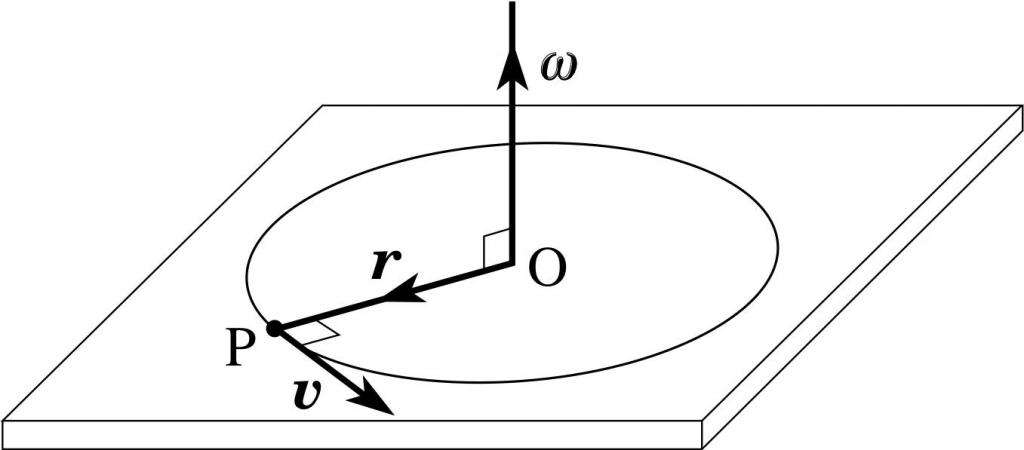
Здесь ω - угловая скорость, которая дальше появится в уравнении моментов. Заметим, что направление вектора T¯ находится по тому же правилу, что и M¯. На рисунке выше T¯ по направлению будет совпадать с вектором угловой скорости ω¯.
Физический смысл величины T¯ является таким же, как и характеристики p¯ в случае линейного движения, то есть момент импульса описывает количество вращательного движения (запасенную кинетическую энергию).
Момент инерции
Третья важная характеристика, без которой невозможно составить уравнение движения вращающегося объекта, - это момент инерции. Появляется он в физике в результате математических преобразований формулы для момента импульса материальной точки. Покажем, как это делается.
Представим величину T¯ в следующем виде:
T¯ = r¯*m*v¯, где p¯ = m*v¯
Пользуясь связью между угловой и линейной скоростями, можно переписать это выражение следующим образом:
T¯ = r¯*m*r¯*ω¯, где v¯ = r¯*ω¯
Последнее выражение запишем в виде:
Величина r2*m - это момент инерции I для точки массой m, которая совершает круговое движение вокруг оси на расстоянии от нее r. Этот частный случай позволяет ввести общее уравнение момента инерции для тела произвольной формы:
I - это аддитивная величина, смысл которой заключается в инерционности вращающейся системы. Чем больше I, тем труднее раскрутить тело, и необходимо приложить значительные усилия, чтобы его остановить.
Уравнение моментов
Мы рассмотрели три величины, название которых начинается со слова "момент". Это сделано было намеренно, поскольку все они связаны в одно выражение, получившее название уравнения 3 моментов. Выведем его.
Рассмотрим выражение для момента импульса T¯:
Найдем, как изменяется величина T¯ во времени, имеем:
Учитывая, что производная угловой скорости равна таковой для скорости линейной, деленной на r, а также раскрывая величину I, приходим к выражению:
dT¯/dt = m*r2*1/r*dv¯/dt = r*m*a¯, где a¯ = dv¯/dt - линейное ускорение.
Заметим, что произведение массы на ускорение - это не что иное, как действующая внешняя сила F¯. В итоге получаем:
Мы пришли к интересному выводу: изменение момента импульса равно моменту действующей внешней силы. Это выражение принято записывать в несколько иной форме:
M¯ = I*α¯, где α¯ = dω¯/dt - угловое ускорение.
Это равенство называется уравнением моментов. Оно позволяет рассчитать любую характеристику вращающегося тела, зная параметры системы и величину внешнего воздействия на нее.
Закон сохранения T¯
Полученный в предыдущем пункте вывод свидетельствует о том, что если внешний момент сил будет равен нулю, то момент импульса меняться не будет. В таком случае запишем выражение:
T¯ = const. или I1*ω1¯ = I2*ω2¯
Эта формула носит название закона сохранения величины T¯. То есть любые изменения внутри системы суммарный момент импульса не меняют.
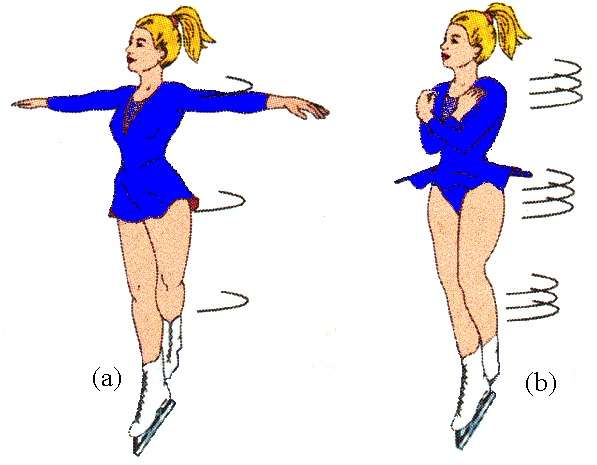
Этот факт используется фигуристами и балеринами во время их выступлений. Также его применяют, если необходимо выполнить поворот вокруг своей оси искусственного спутника, движущегося в космосе.
Читайте также:

