Модель свободных электронов в металле кратко

Обновлено: 02.07.2024

МЕТАЛЛЫ: НЕСТАЦИОНАРНЫЕ ХИМИЧЕСКИЕ СВЯЗИ И ДВА МЕХАНИЗМА ПЕРЕНОСА ЭЛЕКТРИЧЕСТВА

А.А.Гришаев, независимый исследователь

Таким образом, модели современной физики не дают нам даже элементарного понимания принципов, по которым формируются металлические структуры – а, значит, природа электропроводности металлов также остаётся неясной. В данной статье мы делаем попытку прояснить эти вопросы.

Много ли в металлах свободных электронов?

Поразительно, но на основе экспериментальных данных Толмена и Стюарта можно было определить не только знак заряда носителей электричества, которые давали регистрируемый импульс тока, и не только отношение заряда к массе у этих носителей (это авторы проделали), но и количество этих носителей в меди – а этого авторы не проделали. Восполним этот пробел.

Для силы тока I можно записать два выражения: I = Q / t , где Q - заряд, прошедший через поперечное сечение проводника за время t , а также I = en _e VS , где e - элементарный электрический заряд, n _e - концентрация носителей этого заряда, V - средняя скорость их движения, S - площадь поперечного сечения проводника. Приравнивая эти два выражения, для концентрации свободных электронов получаем

n _e =Q/( t eVS ). (1)

t = ( w _p ) -1 = (m_e/4 p n _e e 2 ) 1/2 , (2)

где m _e - масса электрона. Комбинируя (1) и (2) с учётом того, что V = V ₀/2, получаем:

Таким образом, результаты Толмена и Стюарта не только демонстрируют наличие свободных электронов в металлах, но и свидетельствуют о таком ничтожном их количестве, что концепция газа свободных электронов в металлах оказывается совершенно неадекватной реалиям. Кстати, ничтожностью количества свободных электронов в металлах тривиально объясняется, почему теплоёмкость металлов, как и у диэлектрических кристаллов, подчиняется закону Дюлонга и Пти, т.е. почему свободные электроны в металлах не дают заметного вклада в теплоёмкость [5,6].

Связи между атомами металла: предварительные замечания.

Укажем на ещё один факт, сокрушительный для концепции газа свободных электронов в металлах. Этим фактом, проливающим свет на природу связей между атомами металла, является сводка средних величин междуатомных расстояний в металлических кристаллах – которые легко рассчитать на основе справочных значений атомных масс и плотностей. В таблице приведены рассчитанные нами междуатомные расстояния d и удвоенные значения 2 r экспериментальных атомных радиусов (см., например, [7]), а также, в последнем столбце, даны отношения этих пар величин. Обращает на себя внимание то, что все эти отношения близки к единице. На наш взгляд, это свидетельствует о том, что кристаллическая решётка металла формируется при непременном участии самых внешних электронов, входящих в состав атомов – и, значит, структура решётки обусловлена не газом свободных электронов, а химическими связями, базовые принципы которых мы обсуждали в [8].

d /2 r

На первый взгляд, химические связи не могут обеспечить металлическую структуру. Ведь если у атома имеется всего один валентный электрон, то он может образовать одну химическую связь с соседним атомом, тогда как для формирования жёсткой трёхмерной решётки требуется, как минимум, три связи на атом. Конечно же, атом с единственным валентным электроном не может образовать три связи одновременно. Но мы полагаем, что он может образовывать их попеременно, связываясь с соседями по очереди. На наш взгляд, в этом и заключается главный секрет кристаллической структуры металлов: она является динамической, будучи обусловлена попеременными переключениями химических связей между соседними атомами. Тогда мы должны пояснить, как работает механизм, который обеспечивает эти переключения химических связей.

Чем обусловлены переключения химических связей в кристаллах металлов.

Рассмотрим случай металла с наименьшим возможным атомным номером – т.е. случай атома лития, у которого три электрона, из которых только один может участвовать в образовании текущей химической связи.

Некоторые приложения модели динамической структуры металлов.

Два механизма переноса электричества в металлах.

Эксперименты по измерению подвижности свободных электронов в металлах дают, что, при протекании постоянного электрического тока, скорость перемещения роя электронов составля tn миллиметры в секунду [5,17]. Теперь представим двухпроводную линию с длиной, скажем, 10 км, к дальним контактам которой присоединён конденсатор, а к ближним её контактам можно подключить источник постоянного напряжения. После замыкания рубильника, подключающего этот источник, напряжение на конденсаторе появится с задержкой во времени, которая определяется, практически, скоростью света. По традиционной логике, заряды на пластинах конденсатора могут появиться, в данном случае, лишь благодаря перемещениям по проводам свободных электронов. Но, перемещаясь, в совокупности, на миллиметры в секунду, свободные электроны никак не смогут обеспечить то молниеносное установление напряжения на конденсаторе, которое наблюдается на опыте. При таком положении дел, как может наука заявлять, что ей понятен механизм переноса электричества в металлах?

Напротив, мы предлагаем модель этого молниеносного процесса. Эта модель является развитием концепции зарядовых разбалансов [10] – волны которых распространяются в веществе именно со скоростью света [10], причём перенос вещества при этом не происходит. В вышеприведённом примере с конденсатором на конце двухпроводной линии, электрические импульсы, которые формируются зарядовыми разбалансами в атомах проводов, бегут к конденсатору, практически, со скоростью света. Добежав до конденсатора, они сразу же создают напряжение между его пластинами – несколько меньшее, чем напряжение источника, из-за падения напряжения на проводах. Таким образом происходит зарядка конденсатора, которую можно назвать реактивной – обусловленной лишь наведёнными на пластинах конденсатора зарядовыми разбалансами противоположного знака, но не притоком электронов на отрицательную пластину и оттоком их с положительной пластины. Приток-отток электронов – это вторичный эффект, который протекает гораздо медленнее, чем индуцирование зарядовых разбалансов. Но именно этот приток-отток электронов обеспечивает зарядку конденсатора, которую можно назвать активной. Характерное время, требуемое для активной зарядки, определяется постоянной RC -цепочки, т.е. произведением активного сопротивления на ёмкость. Лишь такой, активно заряженный, конденсатор способен дать мощную разрядную искру в воздухе при попытке замкнуть его выводы. Если же, в нашем случае с конденсатором на конце 10-километровой линии, отсоединить его спустя 33 мкс после подключения источника напряжения, то, испытав лишь реактивную зарядку, никакой мощной разрядной искры он не даст.

Как можно видеть, различия в электропроводности у металлов и диэлектриков обусловлены именно наличием свободных электронов в металлах, поскольку волны зарядовых разбалансов в металлах и диэлектриках ничем принципиально не различаются. Через диэлектрические провода не получается активная зарядка конденсатора, поскольку диэлектрические провода не обеспечивают притока-оттока электронов. Но переменный ток, как волны зарядовых разбалансов, проходит через диэлектрики с не меньшей эффективностью, чем через металлы – поскольку омическое сопротивление для волны зарядовых разбалансов равно нулю.

Что такое намагниченность?

Считается, что магнитное действие производят движущиеся электрические заряды, и, соответственно, стационарное магнитное действие производят стационарные движения зарядов, т.е. стационарные токи. Иногда говорят, что магнитное действие производит любой отрезок проводника с током. Это не вполне корректно: реальные токи замкнуты, и следует говорить о магнитном действии замкнутых токов.

Какие замкнутые токи могут быть, например, в намагниченном железе? О движении свободных электроном здесь не может быть и речи – их движение быстро затухло бы из-за омического сопротивления. Официальная наука полагает, что феномен намагниченности объясняется на основе гипотезы о собственном магнитном моменте электрона, т.н. спине – якобы, ориентируясь преимущественно в том или ином направлении, спины электронов в образце создают ненулевой суммарный магнитный момент. Но, на наш взгляд, гипотеза о спине электрона не выдерживает критики. Во-первых, до сих пор нет правдоподобной физической модели механизма собственного магнитного момента у электрона – предлагавшиеся модели оказывались клубками вопиющих противоречий. Во-вторых, никто на опыте не доказал, что электрону действительно присущ собственный магнитный момент. Например, никому не удалось расщепить электронный пучок надвое – в неоднородном магнитном поле. Подобные эффекты получаются с атомами – например, в известном опыте Штерна и Герлаха – причём, здесь расщепление атомного пучка надвое считают результатом действия неоднородного магнитного поля на спины атомарных электронов, имеющие две противоположные ориентации. Не странно ли: действия магнитного поля на спины электронов недостаточно, чтобы растащить эти электроны, но зато достаточно, чтобы растащить атомы, массы которых на четыре порядка больше!

Не используя сказочных представлений о спинах электронов, мы предлагаем модель намагниченности, которая логично следует из концепции зарядовых разбалансов. Мы полагаем, что порождающие намагниченность замкнутые токи обусловлены подвижками зарядовых разбалансов. Соответствующее движение электричества по замкнутым контурам, которое способно поддерживаться неопределённо долго, возможно далеко не в любом образце. Но такая возможность имеется, например, в металлических образцах – благодаря циклическим переключениям химических связей, о которых мы говорили выше. Можно сказать, что химические связи мигрируют по образцу, а вместе с ними способны мигрировать не только колебания зарядовых разбалансов, но и их постоянные составляющие, которыми имитируются ненулевые электрические заряды. Существует огромное множество возможных путей миграций химических связей в конкретном образце, но представляется логичным, что должны иметь место объёмчики, в пределах которых миграции химических связей оказываются упорядочены таким образом, что они следуют, практически, по одним и тем же путям. Соответственно, каждый такой объёмчик может обладать ненулевым суммарным магнитным моментом. Как можно видеть, границы между этими объёмчиками способны достаточно свободно перемещаться, т.е. одни объёмчики способны расти за счёт уменьшения других, откликаясь на внешнее магнитное воздействие – и это происходит без ущерба для макроструктуры образца. Фактически, мы обрисовали поведение доменов в намагничивающихся образцах. Только магнитный момент каждого домена обусловлен, на наш взгляд, не упорядоченностью спинов электронов, а упорядоченностью миграций химических связей, вместе с которыми мигрируют проимитированные электрические заряды.

А есть ли в природе сверхпроводимость?

Небольшое обсуждение.

Как мы постарались показать, главные механические, физические и химические свойства металлов находят непротиворечивое качественное объяснение на основе модели динамической структуры, обусловленной переключениями химических связей между атомами решётки.

1. R.C.Tolman, T.D.Stewart. Phys.Rev., 8 (1916) 97.

2. R.C.Tolman, L.M.Mott-Smith. Phys.Rev., 28 (1926) 794.

3. R.C.Tolman, S.Karrer, E.W.Guernsey. Phys.Rev., 21 (1933) 525.

8. А.А.Гришаев. Новый взгляд на химическую связь и не парадоксы молекулярных спектров. – Доступна на данном сайте.

9. А.А.Гришаев. Зарядовые разбалансы – отличительный признак валентных электронов. – Доступна на данном сайте.

13. S.Knoop, et al. Magnetically Controlled Exchange Process in an Ultracold Atom-Dimer Mixture. Phys.Rev.Lett., 104, 053201 (2010).

18. А.А.Гришаев. Разноимённые электрические заряды, как противофазные квантовые пульсации. – Доступна на данном сайте.

20. Я.И.Френкель. Сверхпроводимость. М.-Л., ОНТИ, 1936.

22. Т.В.Кононенко, и др. Сравнительное исследование абляции материалов фемтосекундными и пико/наносекундными лазерными импульсами. Квантовая электроника, 28, 2 (1999) 167.

23. M . R . H . Knowles , et al . Micro-machining of Metals, Silicon and Polymers using Nanosecond Lasers. International Journal of Advanced Manufactured Technology, 33, № 1-2, May 2007, p. 95-102.

1. Классическая теория электронного газа П. Друде. Формулы Друде для коэффициентов теплопроводности и электропроводности. Теплоемкость классического электронного газа.

2. Закон Видемана-Франца.

3. Квантовая теория металлов А. Зоммерфельда. Одночастичное приближение. Энергетический спектр. Плотность состояний свободных электронов.

4. Заполнение квантовых состояний электронами при абсолютном нуле температуры. Распределение Ферми-Дирака. Свойства свободных электронов при абсолютном нуле температуры. Энергия и поверхность Ферми.

5. Квантовые формулы для коэффициента теплопроводности, электропроводности и теплоемкости электронного газа.

6. Ограниченность модели идеального газа свободных электронов металла.

Одним из эффективных методов анализа свойств сложной системы заключается в ее разделении на несколько более простых подсистем, где каждая подсистема описывается с помощью собственной модели и отвечает за определенные свойства всей системы. В случае твердого тела такими подсистемами являются кристаллическая решетка, магнитные моменты электронов и атомных ядер, коллективизированные валентные электроны, отвечающие соответственно за механические, магнитные и электрические свойства кристалла.

Модель свободных электронов для описания электрических и тепловых свойств металла была предложена П. Друде в 1900г. через 3 года после экспериментального открытия электрона Дж. Дж. Томсоном в 1897г. В качестве свободных коллективизированных электронов, способных перемещаться по всему объему металла, рассматриваются валентные электроны атомов, образующих кристалл. Появление свободных электронов обусловлено взаимодействием внешних электронных оболочек соседних атомов кристаллической решетки, благодаря которому валентные электроны могут покинуть свои атомы и образовать единый коллектив обобществленных всеми ионами кристаллической решетки свободных электронов.

В своей теории П. Друде использовал результаты, полученные для идеального газа частиц, с учетом того, что идеальный газ свободных электронов находится в кристаллической решетке металла. Ионы этой решетки благодаря кулоновскому взаимодействию удерживают свободные электроны внутри металла. С другой стороны, кулоновское взаимодействие свободных электронов с ионами кристаллической решетки стабилизирует эту решетку путем компенсации взаимного отталкивания положительных ионов решетки, создавая металлический тип связи.

В своем движении свободные электроны сталкиваются с ионами кристаллической решетки и обмениваются с ними импульсом и кинетической энергией. Эти столкновения обеспечивают тепловое равновесие между подсистемой свободных электронов и решеткой, поэтому в случае теплового равновесия металла следует считать, что электронная температура T_э равна решеточной T_р, т.е. T_э = T_р = T, где T - температура металла.

Необходимо отметить, что модель идеального газа свободных электронов применима только тогда, когда средняя энергия кулоновского взаимодействия свободных электронов, приходящаяся на один электрон, много меньше средней кинетической энергии поступательного движения электрона. В классической теории электронного газа металла это условие не выполняется, тем не менее в подходе П. Друде используется именно модель идеального газа, поскольку она правильно описывает некоторые опытные факты. Только квантовая теория металлов позволяет в определенной степени обосновать справедливость применения модели идеального газа.

Вычисление на основе модели свободных электронов электропроводности и коэффициента теплопроводности металлов требует конкретизации характера столкновений электронов с ионами кристаллической решетки. П. Друде сделал следующие допущения:

1) между столкновениями с ионами электроны движутся согласно законам классической механики;

2) в каждом столкновении электрон теряет всю кинетическую энергию направленного (дрейфового) движения, приобретенную в результате действия внешней силы (кинетическая энергия теплового движения при учете большого числа столкновений в среднем сохраняется неизменной благодаря равенству температур T_э = T_р);

3) электрон сталкивается с каждым ионом кристаллической решетки, который встречается на траектории его движения, поэтому среднее время между двумя последовательными столкновениями , где d – расстояние между соседними ионами (период кристаллической решетки), – средняя скорость теплового движения электрона, Дж/К - постоянная Больцмана, кг – масса электрона.

На основе сделанных допущений была выведена следующая формула для электропроводности σ металла

где Кл – заряд электрона, n – концентрация свободных электронов (число свободных электронов в единице объема). Для хороших металлов 1/м 3 . Если в (6.1) подставить соответствующие значения этих параметров, легко получить, что для хороших металлов 1/Ом·м, что соответствует опытным данным для металлов при комнатной температуре.

Формула (6.1) может быть получена следующим образом. Во внешнем электростатическом поле функция распределения свободных электронов по скоростям отличается от максвелловской и имеет вид

где c – нормировочная постоянная, , T – температура электронов, τ - время свободного пробега электронов, в течение которого они приобретают дополнительную энергию за счет взаимодействия с внешним полем.

Данная функция распределения соответствует направленному движению электронов с плотностью тока

где n - концентрация свободных электронов, τ - среднее время свободного пробега электронов и

– электропроводность газа свободных электронов.

Среднее время τ свободного пробега электронов зависит от процессов рассеяния электронов на тепловых колебаниях кристаллической решетки, примесях и дефектах кристалла. Столкновения электронов друг с другом, а также с неподвижными ионами в узлах кристаллической решетки на электропроводность не влияют.

Для коэффициента теплопроводности χ_T газа свободных электронов П.Друде использовал выражение, полученное в кинетической теории идеального газа,

Из (6.1) и (6.2) следует соотношение

выражающее закон Видемана-Франца, полученный экспериментально для металлов в 1853г. Данное соотношение является универсальным и справедливым для всех металлов, поскольку в правую часть соотношения (6.3) входят только фундаментальные физические постоянные k и e.

Согласно классической теории теплоемкости газов молярная теплоемкость при постоянном объеме для свободных электронов

где Дж/К - универсальная газовая постоянная, не зависит от температуры и имеет одинаковую величину для всех металлов. Экспериментальные исследования показали, что линейно зависит от температуры, причем при комнатной температуре величина примерно в 100 раз оказалась меньше теоретического значения (6.4).

Возникшие противоречия в классической теории теплоемкости электронного газа металлов удалось устранить в квантовой теории металлов, разработанной А.Зоммерфельдом в 1927-28гг., где была сохранена модель свободных электронов, но движение электронов описывалось законами квантовой механики.

В одночастичном приближении задача нахождения стационарных состояний всего коллектива свободных электронов сначала решается только для одного электрона, находящегося в суммарном электрическом поле всех ионов кристаллической решетки и всех свободных электронов, исключая данный электрон. Однако решить соответствующее уравнение Шредингера практически невозможно в силу его сложности.

Для преодоления этих трудностей используется специальный прием, который заключается в учете только наиболее существенных свойств взаимодействия электрона с суммарным электрическим полем при помощи граничных условий для волновой функции электрона. Один из основных результатов взаимодействия электрона с суммарным электрическим полем заключается в том, что электрон движется в ограниченной области пространства, которая определяется размерами металла.

Этот результат нашел свое выражение в виде модели движения электрона в бесконечно глубокой потенциальной яме, имеющей для простоты прямоугольную форму. В одномерном случае соответствующее распределение потенциала U имеет вид, показанный на рисунке 6.1. Внутри потенциальной ямы потенциал U=0 и частица обладает только кинетической энергией. За пределами потенциальной ямы x L потенциальная энергия бесконечно велика, поэтому вероятность обнаружения частицы в этих областях

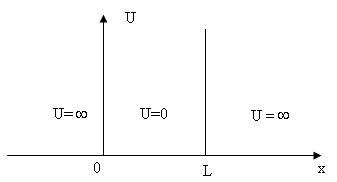
Рис. 6.1

равна нулю. Следовательно, граничные условия для волновой функции ψ частицы принимают вид: , если или .

Решение стационарного уравнения Шредингера для трехмерной бесконечно глубокой прямоугольной потенциальной ямы с линейными размерами L₁, L₂, L₃ дает дискретный энергетический спектр единичного электрона в виде

где n₁, n₂ и n₃ = 1,2,3,… – квантовые числа, Дж с – постоянная Планка, .

Если линейные размеры металла достаточно большие, то энергетический спектр (6.5) можно считать непрерывным и совпадающим с энергетическим спектром свободного электрона в неограниченной области

где - импульс электрона, - волновое число, λ - длина волны де Бройля.

Квантовый характер движения электрона проявляется в том, что оно характеризуется определенной энергетической плотностью стационарных состояний

которая дает число стационарных состояний электрона, приходящихся на единичный интервал энергии с центром в точке ε при рассмотрении единичного объема пространства. Формула (6.7) имеет асимптотический характер, когда объем металла очень большой и величина Z(ε) практически не зависит от формы кристалла и граничных условий для волновой функции на поверхности кристалла.

Теперь необходимо задать распределение электронов по энергетическим уровням стационарных состояний. Поскольку электроны имеют спин s = 1/2 и относятся к фермионам, они подчиняются статистике Ферми – Дирака и для них справедлив запрет Паули: в одном квантовом состоянии может находиться не более 1 электрона. В нашем случае энергия стационарных состояний электрона не зависит от ориентации его спина, поэтому они являются вырожденными. В результате одно стационарное состояние могут занимать 2 электрона с противоположно ориентированными спинами. Это обстоятельство учтено в (6.7).

Если свободные электроны находятся в состоянии теплового равновесия при температуре Т, то необходимо знать среднее число электронов , находящихся в квантовом состоянии с энергией ε_i. Искомое среднее число электронов определяется распределением Ферми – Дирака

Здесь μ - химический потенциал системы частиц, который находится из условий нормировки:

где N – полное число фермионов в системе, суммирование ведется по всем стационарным состояниям.

Рассмотрим основное состояние свободных электронов при абсолютном нуле температуры T=0K, когда энергия системы минимальна. В этом случае распределение Ферми – Дирака имеет прямоугольную форму, как показано на рис.6.2.

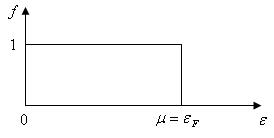
Рис. 6.2

Максимальная энергия свободных электронов металла при T=0K называется энергией Ферми, а ее величина находится с помощью условия нормировки при заданной концентрации электронов n

Другие характеристики газа свободных электронов при T=0K выражаются через энергию Ферми:

1) плотность энергии

2) средняя энергия одного электрона

3) средняя скорость движения электрона

4) давление электронного газа

В формулах (6.11) – (6.15) единственной индивидуальной характеристикой металла является концентрация n свободных электронов.

Типичные значения этих величин (если принять 1/м 3 ) следующие:

Таким образом, даже при абсолютном нуле температуры средняя скорость движения свободных электронов металла примерно на 3 порядка превышает скорость звука в металле ( м/с), а давление газа свободных электронов на 5 порядков превышает атмосферное. В формулах Друде (6.1) и (6.2) использовалась средняя скорость теплового движения электронов, которая при комнатной температуре К на порядок меньше величины фермиевской скорости . Кроме того, необходимо отметить, что именно большая величина позволяет в определенном смысле пренебречь энергией кулоновского взаимодействия электронов и использовать модель свободного электронного газа.

Важной характеристикой свободных электронов металла является поверхность Ферми, определяемая для T=0K. Эта поверхность распложена в пространстве импульсов, где вдоль осей декартовой системы координат откладываются проекции импульсов p_x, p_y, p_z свободных электронов. Изоэнергетическая поверхность (поверхность постоянной энергии)

отделяющая в пространстве импульсов состояния, занятые электронами, от незанятых, называется поверхностью Ферми. В рассмотренном выше случае поверхность Ферми для T=0K есть сферическая поверхность радиусом с центром в точке . Величина называется импульсом Ферми.

В общем случае геометрические свойства поверхности Ферми зависят от специфики взаимодействия свободных электронов с ионами кристаллической решетки и могут быть очень сложными. Для определения геометрии поверхности Ферми используются, главным образом, магнитные эффекты, связанные с взаимодействием свободных электронов вблизи этой поверхности с внешним магнитным полем. Получаемые таким способом геометрические образы позволяют сделать результаты электронной теории металлов более наглядными по сравнению с формулами.

При T>0K появляются свободные электроны за пределами поверхности Ферми, соответствующей T=0K, и имеющие энергию . В тепловых процессах основную роль играют свободные электроны с энергиями . На рис. 6.3 приведен график распределения

Рис. 6.3

Ферми-Дирака для случая T>0K, на котором штриховкой отмечена область энергий тех свободных электронов, которые играют главную роль в тепловых процессах.

Модель свободных электронов, также известна как модель Зоммерфельда или модель Друде-Зоммерфельда, — простая квантовая модель поведения валентных электронов в атоме металла, разработана Арнольдом Зоммерфельдом на основе классической модели Друде с учётом квантово-механической статистики Ферми — Дирака. Электроны металла рассматриваются в этой модели как Ферми-газ.

Отличие модели Зоммерфельда от модели Друде в том, что в кинетических процессах участвуют не все валентные электроны металла, а только те, которые имеют энергию в пределах k B T T> от энергии Ферми, где k B > — постоянная Больцмана , T — температура. Это ограничение возникает благодаря принципу Паули, запрещающему электронам иметь одинаковые квантовые числа. Как следствие при конечных температурах состояния с низкими энергиями заполнены, что препятствует электронам изменить свою энергию или направление движения.

Плотность состояний трёхмерного газа фермионов пропорциональна квадратному корню из кинетической энергии частиц.

Несмотря на свою простоту, модель объясняет много разных явлений, среди которых:

В § 78 2-го тома была изложена элементарная классическая теория свободных электронов в металле. Теперь познакомимся с основами квантовой теории.

Согласно модели свободных электронов валентные электроны атомов металла могут свободно перемещаться в пределах образца. Именно валентные электроны обусловливают электропроводность металла, и по этой причине их называют электронами проводимости.

Рассмотрим образец металла, который для простоты будем считать имеющим форму куба со стороной L. Допустим, что электроны проводимости движутся в пределах образца совершенно свободно. Положив в формуле (21.4) , получим уравнение Шрёдингера для свободного электрона:

(m — масса электрона).

Легко проверить подстановкой, что решение уравнения имеет вид

где есть волновой вектор электрона, связанный с энергией соотношением

Условие нормировки пси-функции запишется следующим образом (интегрирование производится по объему образца V, равному :

Полагая С вещественным, получим для него значение Подстановка в (51.2) дает

Пси-функция должна удовлетворять граничным условиям, которые заключаются в требовании, чтобы она была периодической по х, у, z с периодом L. Легко убедиться в том, что функция (51.4) будет удовлетворять этим условиям при значениях компонент волнового вектора, равных

где — целые числа, принимающие независимо друг от друга значения и т. д. Действительно, подстановка значений (51.5) в (51.4) дает

Замена через либо у через у + L и т. д. оставляет оункцию без изменений (появляется лишь множитель, равный.

Таким образом, значения волнового вектора квантуются. Соответственно квантуется и энергия электрона проводимости металле . Подстановка значений (51.5) в формулу (51.3) приводит к следующему выражению для энергии:

Состояние электрона проводимости определяется значением волнового вектора к (т. е. значениями ) и спиновым квантовым числом Следовательно, состояние можно задать четырьмя квантовыми числами: Энергия электрона определяется суммой квадратов квантовых чисел гц. Одной и той же сумме квадратов соответствует (кроме случая ) несколько различных комбинаций чисел т. Следовательно, уровни энергии являются вырожденными. Уровень имеет кратность вырождения, равную двум Следующий уровень реализуется при 12 различных комбинациях квантовых чисел (см. табл. 51.1), уровень — при 24 комбинациях и т. д. Таким образом, с ростом энергии увеличивается число различных состояний, отвечающих данному значению Е.

Введем воображаемое пространство, по осям которого будем откладывать значения квантовых чисел . В этом пространстве каждой паре состояний (отличающихся значениями ) соответствует точка. Поверхность равных значений энергии имеет форму сферы радиуса Число состояний энергия которых не превышает значения (см. (51.6)), равно удвоенному количеству точек, содержащихся внутри сферы радиуса . Поскольку точки расположены с плотностью, равной единице, определяется удвоенным объемом сферы:

Исключив из (51.6) и (51.7) сумму квадратов чисел получим

— объем образца металла). Полученная нами формула определяет число состояний, энергия которых не превышает значение Е.

Из соотношения (51.8) вытекает, что

Здесь есть число состояний с энергией, заключенной в интервале от до . Следовательно, плотность состояний , т. е. число состояний, приходящееся на единичный интервал энергии, равно

Пусть число свободных электронов в единице объема металла равно . Тогда в образце металла будет содержаться свободных электронов. Вследствие принципа Паули при абсолютном нуле эти электроны расположатся по одному в каждом состоянии на самых низких энергетических уровнях. Поэтому все состояния с энергией Е, меньшей некоторого значения будут заполнены электронами, состояния же с будут вакантными. Энергия называется у ров нем Ферми при абсолютном нуле. В следующем параграфе будет показано, что уровень Ферми играет роль параметра в распределении электронов по состояниям с различи ной энергией. Этот параметр слабо зависит от температуры. Величина представляет собой значение параметра при .

Изоэнергетическая поверхность в пространстве (или, что то же самое, в -пространстве; ), соответствующая значению энергии, равному носит название поверхности Ферми. В случае свободных электронов эта поверхность описывается уравнением

[(см. (51.3)) и, следовательно, имеет форму сферы. При абсолютном нуле температуры поверхность Ферми отделяет состояния, заполненные электронами, от незаполненных состояний.

Значение можно найти, положив в формуле (51.8), :

Оценим значение Концентрация электронов проводимости в металлах лежит в пределах от до Взяв для среднее значение получим

Найдем среднюю энергию электронов при абсолютном нуле. Суммарная энергия электронов, заполняющих состояния с энергиями от Е до , определяется выражением

Суммарная энергия всех электронов проводимости равна

Разделив эту энергию на полное число электронов, равное , получим среднюю энергию одного электрона:

Подстановка выражения (51.9) для дает

Для мы получили значение порядка 5 эВ. Следовательно, средняя энергия электронов проводимости при абсолютном нуле составляет примерно 3 эВ. Это огромная величина. Чтобы сообщить классическому электронному газу такую энергию, его нужно нагреть до температуры порядка 25 тысяч кельвин.

Теперь можно объяснить, почему электронный газ вносит очень малый вклад в теплоемкость металлов. Средняя энергия теплового движения, равная по порядку величины составляет при комнатной температуре . Такая энергия может возбудить только электроны, находящиеся на самых верхних уровнях, примыкающих к уровню Ферми. Основная масса электронов, размещенных на более глубоких уровнях, останется в прежних состояниях и поглощать энергию при нагревании не будет. Таким образом, в процессе нагревания металла участвует лишь незначительная часть электронов проводимости, чем и объясняется малая теплоемкость электронного газа в металлах.

На рис. 51.1 показан график функции (51.9). Заштрихованная площадь дает число состояний, заполненных электронами при абсолютном нуле. Нагревание металла сопровождается переходом электронов с уровней, примыкающих к уровню Ферми, на уровни, лежащие выше . В результате резкий край заштрихованной фигуры на рис. 51.1 будет размыт. Кривая заполнения уровней электронами примет в этой области вид, показанный пунктирной линией. Площадь под этой кривой остается той же, какой она была при абсолютном нуле (площадь равна ). Область размытия имеет ширину порядка Следовательно, в процессе нагревания металла будет участвовать доля электронов, равная приблизительно где

— величина, называемая температурой Ферми.

В результате теплоемкость электронов составит

При комнатной температуре примерно в 100 раз меньше классического значения ().

Читайте также: