Корень n ой степени и его свойства кратко

Обновлено: 03.07.2024

Чтобы успешно использовать на практике операцию извлечения корня, нужно познакомиться со свойствами этой операции.
Все свойства формулируются и доказываются только для неотрицательных значений переменных, содержащихся под знаками корней.

Теорема 1. Корень n-й степени (n=2, 3, 4. ) из произведения двух неотрицательных чипсел равен произведению корней n-й степени из этих чисел:

1. Теорема 1 остается справедливой и для случая, когда подкоренное выражение представляет собой произведение более чем двух неотрицательных чисел.

Теорема 2. Если, и n - натуральное число, большее 1, то справедливо равенство

Краткая (хотя и неточная) формулировка, которую удобнее использовать на практике: корень из дроби равен дроби от корней.

Теорема 1 позволяет нам перемножать только корни одинаковой степени, т.е. только корни с одинаковым показателем.

Теорема 3. Если , k - натуральное число и n - натуральное число, большее 1, то справедливо равенство

Иными словами, чтобы возвести корень в натуральную степень, достаточно возвести в эту степень подкоренное выражение.
Это — следствие теоремы 1. В самом деле, например, для к = 3 получаем: Точно так же можно рассуждать в случае любого другого натурального значения показателя к.

Теорема 4. Если , k, n - натуральные числа, большее 1, то справедливо равенство

Иными словами, чтобы извлечь корень из корня, достаточно перемножить показатели корней.
Например,

Будьте внимательны! Мы узнали, что над корнями можно осуществлять четыре операции: умножение, деление, возведение в степень и извлечение корня (из корня). А как же обстоит дело со сложением и вычитанием корней? Никак.
Например, вместо нельзя написать В самом деле, Но ведь очевидно, что

Теорема 5. Если показатели корня и подкоренного выражения умножить или разделить на одно и то же натуральное число, то значение корня не изменится, т.е.

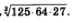
Пример 1. Вычислить

Решение. Воспользовавшись первым свойством корней (теорема 1), получим:

Пример 2. Вычислить
Решение. Обратим смешанное число в неправильную дробь.
Имеем Воспользовавшись вторым свойством корней (теорема 2), получим:

Пример 3. Вычислить:

(показатели корня и подкоренного выражения разделили на 4);

(показатели корня и подкоренного выражения разделили на 3);

(показатели корня и подкоренного выражения умножили на 2).
решении примера 5, где требовалось выполнить умножение корней с разными показателями:

Пример 5. Вычислить

Решение. Вот как обычно рассуждают в подобных случаях.
1) По теореме 5 в выражении можно и показатель корня (т.е. число 2) и показатель подкоренного выражения (т.е. число 1) умножить на одно и то же натуральное число. Воспользовавшись этим, умножим оба показателя на 3; получим:
2) По теореме 5 в выражении можно и показатель корня (т.е. число 3) и показатель подкоренного выражения (т.е. число 1) умножить на одно и то же натуральное число. Воспользовавшись этим, умножим оба показателя на 2; получим:
3) Поскольку получили корни одной и той же 6-й степени, то можно их перемножить:

Задание № 1
Скачай задание из Приложений к странице. Распечатай, выполни предложенные задания, отсканируй и отошли учителю

Задание № 2
Скачай задание из Приложений к странице. Распечатай, выполни предложенные задания, отсканируй и отошли учителю .
Упростите:

Задание № 3
Скачай задание из Приложений к странице. Распечатай, выполни предложенные задания, отсканируй и отошли учителю .
Избавьтесь от иррациональности в знаменателе:

Задание № 4
Скачай задание из Приложений к странице. Распечатай, выполни предложенные задания, отсканируй и отошли учителю .

Задание № 5
Скачай задание из Приложений к странице. Распечатай, выполни предложенные задания, отсканируй и отошли учителю .

Задание № 6
Скачай задание из Приложений к странице. Распечатай, выполни предложенные задания, отсканируй и отошли учителю .

Задание № 7
Скачай задание из Приложений к странице. Распечатай, выполни предложенные задания, отсканируй и отошли учителю .

Определение корня n-й степени из действительного числа

Корнем n-й степени ($n=2, 3, 4, 5, 6… $) некоторого числа $a$ называют такое неотрицательное число $b$, которое при возведении в степень $n$ дает $a$:

Число $n$ при этом называют показателем корня.

Если $n=2$, то перед вами корень 2-й степени или обычный квадратный корень.

Если $n=3$, то корень 3-й степени и т.д.

Операция извлечения корня n-й степени является обратной к операции возведения в n-ю степень.

Кубический корень из числа 27 равняется 3. Действительно, если число 3 возвести в 3-ю степень, то мы получим 27.

Корень 4-й степени из 16-и равен 2. Двойка в 4-й степени равна 16.

Если извлечь корень n-й степени из 0, всегда будет 0.

Мы не можем в уме подобрать такое число, которое при возведении в 3-ю степень даст 19. Если посчитать на калькуляторе, то получим $2,668…$ – иррациональное число с бесконечным количеством знаков после запятой.

Обычно, в математике, когда у вас получается иррациональное число, корень не считают и оставляют так как есть $\sqrt[3]$.

Что же делать, если под рукой нет калькулятора, а нужно оценить, чему равен такой корень. В этом случае нужно подобрать справа и слева такие ближайшие числа, корень из которых посчитать можно:

$$ \sqrt[3] \le \sqrt[3] \le \sqrt[3] $$ $$ 2 \le \sqrt[3] \le 3 $$

Получается, что наш корень лежит между числами 2 и 3.

Корень четной и нечетной степени

Надо четко различать правила работы четными и нечетными степенями. Дело в том, что корень четной степени можно взять только из положительного числа. Из отрицательных чисел корень четной степени не существует.

Корень нечетной степени можно посчитать из любых действительных чисел. Иногда в школьной программе встречаются задания, в которых требуется определить имеет ли смысл выражение:

Данное выражение имеет смысл, так как корень нечетной степени можно посчитать из любого числа, даже отрицательного.

Так как корень четной степени, а под корнем стоит отрицательное число, то выражение не имеет смысла.

Свойства корня n-й степени

Пусть есть два неотрицательных числа a и b, для них будут выполняться следующие свойства:

Данная статья представляет собой совокупность детальной информации, которая касается темы свойства корней. Рассматривая тему, мы начнем со свойств , изучим все формулировки и приведем доказательства. Для закрепления темы мы рассмотрим свойства n -ой степени.

Свойства корней

Мы поговорим о свойствах .

Свойство умноженных чисел a и b , которое представляется как равенство a · b = a · b . Его можно представить в виде множителей, положительных или равных нулю a 1 , a 2 , … , a k как a 1 · a 2 · … · a k = a 1 · a 2 · … · a k ;
из частного a : b = a : b , a ≥ 0 , b > 0 , он также может записываться в таком виде a b = a b ;
Свойство из степени числа a с четным показателем a 2 · m = a m при любом числе a , например, свойство из квадрата числа a 2 = a .

В любом из представленных уравнений можно поменять части до и после знака тире местами, например, равенство a · b = a · b трансформируется как a · b = a · b . Свойства для равенства часто используются для упрощения сложных уравнений.

Доказательство первых свойств основано на определении квадратного корня и свойствах степеней с натуральным показателем. Чтобы обосновать третье свойство, необходимо обратиться к определению модуля числа.

Первым делом, необходимо доказать свойства квадратного корня a · b = a · b . Согласно определению , необходимо рассмотреть, что a · b - число, положительное или равное нулю, которое будет равно a · b при возведении в квадрат. Значение выражения a · b положительно или равно нулю как произведение неотрицательных чисел. Свойство степени умноженных чисел позволяет представить равенство в виде ( a · b ) 2 = a 2 · b 2 . По определению квадратного корня a 2 = a и b 2 = b , то a · b 2 = a 2 · b 2 = a · b .

Аналогичным способом можно доказать, что из произведения k множителей a 1 , a 2 , … , a k будет равняться произведению квадратных корней из этих множителей. Действительно, a 1 · a 2 · … · a k 2 = a 1 2 · a 2 2 · … · a k 2 = a 1 · a 2 · … · a k .

Из этого равенства следует, что a 1 · a 2 · … · a k = a 1 · a 2 · … · a k .

Рассмотрим несколько примеров для закрепления темы.

3 · 5 2 5 = 3 · 5 2 5 , 4 , 2 · 13 1 2 = 4 , 2 · 13 1 2 и 2 , 7 · 4 · 12 17 · 0 , 2 ( 1 ) = 2 , 7 · 4 · 12 17 · 0 , 2 ( 1 ) .

Необходимо доказать свойство арифметического квадратного корня из частного: a : b = a : b , a ≥ 0 , b > 0 . Свойство позволяет записать равенство a : b 2 = a 2 : b 2 , а a 2 : b 2 = a : b , при этом a : b является положительным числом или равно нулю. Данное выражение и станет доказательством.

Например, 0 : 16 = 0 : 16 , 80 : 5 = 80 : 5 и 3 0 , 121 = 3 0 , 121 .

Рассмотрим свойство квадратного корня из квадрата числа. Его можно записать в виде равенства как a 2 = a Чтобы доказать данное свойство, необходимо подробно рассмотреть несколько равенств при a ≥ 0 и при a 0 .

Очевидно, что при a ≥ 0 справедливо равенство a 2 = a . При a 0 будет верно равенство a 2 = - a . На самом деле, в этом случае − a > 0 и ( − a ) 2 = a 2 . Можно сделать вывод, a 2 = a , a ≥ 0 - a , a 0 = a . Именно это и требовалось доказать.

Рассмотрим несколько примеров.

5 2 = 5 = 5 и - 0 , 36 2 = - 0 , 36 = 0 , 36 .

Доказанное свойство поможет дать обоснование a 2 · m = a m , где a – действительное, а m –натуральное число. Действительно, свойство возведения степени позволяет заменить степень a 2 · m выражением ( a m ) 2 , тогда a 2 · m = ( a m ) 2 = a m .

Это то же самое, что и корень $n$ -ой степени, но разница в том, что арифметический корень из неотрицательного числа есть неотрицательное число!

Арифметическим корнем $n$ -ой степени из числа $a$ называют неотрицательное число, $n$ -я степень которого равна $a$ .

Пример 1. $\sqrt=9 \ (9^2=81); \ \sqrt[\large 3\normalsize] = 3 \ (3^3=27);\ \sqrt[\large 4\normalsize] = 5 \ (5^4=625)$ .

Если $n$ – нечетное число, то существует единственный корень $n$ -й степени из любого числа (положительного или отрицательного). Например, $\sqrt[\large 3\normalsize]=-2; \ \sqrt[\large 3\normalsize]=2$ .

Если $n$ – четное число, то существует два корня $n$ -й степени из любого положительного числа. Например, корень четвертой степени из числа 625 – это числа –5 и 5. Так как $(5)^4=625 \ и \ (-5)^4=625$ .

Корень четной степени из отрицательного числа не существует. Например, $\sqrt[\large 2\normalsize]$ – не имеет смысла.

Для корней нечетной степени справедливо равенство $\sqrt[\large n\normalsize]=-\sqrt[\large n\normalsize]$ .

Основные свойства корней

Извлечением корня $n$ -ой степени называется действие, с помощью которого отыскивается корень $n$ -ой степени. Извлечение корня $n$ -ой степени является обратным действием к возведению в $n$ -ую степень.

Извлечение корня из степени: $\sqrt[\large n\normalsize]>> = >>$ .
Двойное извлечение корня: $\sqrt[\large m\normalsize]<<\sqrt[\large n\normalsize]>> = \sqrt[<\large mn\normalsize>]$ .

Формулы сложных радикалов:

Решение: Запишем показатели степеней рациональными числами и преобразуем их: $\sqrt[\large 3\normalsize]>>>=(a^\cdot b^)^\frac13=(a^6\cdot b^3)^\frac13=(a^6)^\frac13\cdot (b^3)^\frac13=a^\frac63\cdot b^\frac33=a^2b$ .

Пример 3. Освободиться от иррациональности в знаменателе дроби: $\frac1<\sqrt[\large 3\normalsize]<2>-1>$ .

Решение: Имеем иррациональность 3-й степени, поэтому и числитель, и знаменатель умножим на неполный квадрат суммы чисел $\sqrt2$ и 1, тогда в знаменателе получим разность кубов, которая и ликвидирует иррациональность.

Ответ: $\sqrt[\large 3\normalsize]+ \sqrt[\large 3\normalsize]+1$ .

$5\sqrt[\large 3\normalsize]>-3\sqrt[\large 3\normalsize]>-11\sqrt[\large 6\normalsize]+2\sqrt[\large 3\normalsize]>$

Корнем n-ой степени из неотрицательного числа a (n=2, 3, 4. ) называют такое неотрицательное число, при возведении которого в степень n получается число a.

Число a называют подкоренным числом, число n — показателем корня. Важно, что корень четной степени существует только из положительных чисел, а корень нечетной — как из положительных, так и отрицательных, поэтому выражение - 27 4 не имеет смысл, а тот же корень третьей степени имеет — - 27 3 = - 3 .

В алгебре корни нужны для более сокращенных и точных подсчетов, т.к самый простой корень из числа 3 будет равен длинной десятичной дроби, округлив которую получим лишь приблизительное значение. Такие числа называются иррациональными и намного удобнее представить их в виде радикала.

Знак радикала как раз и используют для обозначения корня.

Основные свойства

Основные свойства корня n-ой степени с примерами:

( a n ) n = a , n - ч е т н о a , n - н е ч е т н о Корень n-ой степени и возведение в эту же степень, эти операции являются взаимопоглощающими, поэтому при извлечении корня и возведении значения в степень, получаем искомое число a. Пример: вычислите значение выражения ( - 5 , 8 3 ) 3 . По свойству получаем значение выражения равному -5,8.
a b n = a n * b n , a ≥ 0 , b ≥ 0 . Пример: найти значение выражения: 25 3 * 5 3 = 25 * 5 = 125 3 3 = 25 .
a b n = a n b n , a ≥ 0 , b > 0 . Пример: найти значение выражения 27 8 3 = 27 3 8 3 = 3 2 .
( a n ) k = a n k . Пример: найти значение выражения: ( 2 3 ) 6 = 2 3 6 = 64 3 = 4 .
a k n = a n k , a ≥ 0 . Пример: найти значение выражения: 729 2 3 = 729 3 * 2 = 729 6 = 3 .
a k p n p = a k n , a ≥ 0 . Пример: найти значение выражения: 8 6 9 = 8 3 * 2 3 * 3 = 8 2 3 = 64 3 = 4 .
- a n = - a n , n - н е ч е т н о . Пример: найти значения корня: - 27 3 = - 27 3 = - 3

Область определения корня, пояснение на примерах

Под областью определения в математике понимают множество допустимых для конкретного выражения значений неизвестной переменной (x).

Для корня n-ой степени область определения меняется в зависимости от значения показателя корня.

Если n — четное число, где, n = 2m, где m ∈ N, то область определения — это множество всех действительных неотрицательных чисел D ( x 2 * m ) = [ 0 ; + ∞ ) .

Если показатель корня нечетное число больше единицы, то есть, n = 2m+1, то область определения корня — множество всех действительных чисел D ( x 2 * m + 1 ) = ( - ∞ ; + ∞ ) .

Рассмотрим несколько примеров на определение области определения выражений содержащих корень:

Найти область определения функции f ( x ) = 1 x 2 + 4 x + 3 . Решение: т.к. подкоренное выражение с корнем четной степени (n=2) должно быть положительным, то необходимо решить неравенство x 2 + 4 x + 3 > 0 . Неравенство является строгим, потому что знаменатель дроби не может быть равен нулю. После результатам решения неравенства получим область определения D ( f ) = ( - ∞ ; - 3 ) ∪ ( - 3 ; + ∞ ) .
Найти область определения функции y = 12 - 2 x 6 . Решение: подкоренное выражение из корня четной степени должно быть больше или равно нулю, отсюда следует 12 - 2 x ≥ 0 , о т к у д а x ≤ 6 .
Найти область определения функции y = 3 x - 6 - 25 - x 3 . Решение: функция содержит два выражения под корнем и областью определения будет пересечения областей определения каждого подкоренного выражения, однако подкоренное выражение s q r t [ 3 ] 25 - x может любое значение (т.к показатель степени у корня нечетный). Значит для определения области определения всего выражения будет достаточно только указать область определения выражения для подкоренного выражения 3 x - 6 . Получим 3 x - 6 ≥ 0 , j n r e l f x ≥ 2 .

Метод оценки значения

Не из всех чисел можно извлечь челочисленный корень, в таком случае необходимо приблизительно оценить значение этого корня. Методом оценки значения корня является метод подбора левой и правой границ, т.е. целочисленных значений, корень из которых мы можем извлечь.

Рассмотрим пример: оценить значение 19 . Найдем ближайшие числа большие и меньшие 19, из которых извлекается целочисленный корень, это соответственно 25 и 16, тогда имеем: 16 19 25 , значит 4 19 5 . Значение корня извлеченного из 19 находится в промежутке между 4 и 5.

Рассмотрим еще один пример: оценить значение выражения 19 3 . Найдем ближайшие целочисленные границ, из которых можем извлечь кубический корень, получим: 8 3 19 3 27 3 , значит 2 19 3 3 . Значение кубического корня, извлеченного из числа 19 находится в промежутке между 2 и 3.

Задания для самопроверки

Выполним ряд заданий для проверки и закрепления работы с корнями n-ой степени.

Найти значение выражения 121 * 64 .

Решение: применим свойство произведения корней a b n = a n * b n , получим 121 * 64 = 11 * 8 = 88 .

Решить неравенство ( x - 2 ) 2 ≤ 4 .

Решение: применим свойство корня , тогда неравенство примет вид: ( x - 2 ) ≤ 4 или - 4 ≤ x - 2 ≤ 4 , решая двойное неравенство получим — - 2 ≤ x ≤ 6 .

Найти значение выражения 16 81 4 .

Решение: применим свойство корня a b n = a n b n , получим 16 4 81 4 = 2 3 .

Указать имеет ли смысл выражение - 27 3 .

Решение: вспомним какие числа являются область определения для корня нечетной степени, эти числа — любые, отсюда следует, что выражение - 27 3 имеет смысл.

Указать при каких значениях переменной у имеет смысл выражение 1 y - 1 .

Решение: чтобы определить все допустимые значения переменной необходимо обеспечить выполнение двух условий.

Подкоренное выражение из корня четной степени принимает неотрицательные значения, второе в дроби знаменатель не может быть равен нулю, тогда получим систему: y ≥ 0 y - 1 ≢ 0

Решая эту систему, получим y ≥ 0 y ≢ 1 . Значит выражение имеет смысл при всех у больше или равных нулю, исключая единицу.

Оцените значение выражения 124 4 .

Решение: Найдем ближайшие левую и правую границы, из которых можно извлечь целочисленный корень четвертой степени, получим 81 4 124 4 256 4 или 3 124 4 4 .

Читайте также: