Каково направление равнодействующей силы в силовом многоугольнике кратко

Обновлено: 05.07.2024

ПССС- это система сил, линии действия которых лежат в одной плоскости и пересекаются в одной точке. ПССС можно сложить геометрическим способом, который называется способом силового многоугольника.

Последовательно вычерчивают векторы сил, заданной системы один за другим и получают ломаную линию, которую необходимо замкнуть. Замыкающий вектор соединяет начало первого вектора с концом последнего и направлен ему навстречу.

Полученный многоугольник АВСDEK называется – силовым многоугольником.

Геометрическая сумма всех сил данной системы называется главным вектором этой системы F_гл.

Замыкающая сторона (АК) полученного силового многоугольника является равнодействующей данной системы сил. Следовательно- равнодействующая ПССС равна главному вектору этой системы сил.

ГЕОМЕТРИЧЕСКОЕ УСЛОВИЕ РАВНОВЕСИЯ:

Система СС уравновешена тогда и только тогда, когда силовой многоугольник замкнут, т.е. равнодействующая равна нулю.

Проекция силы на ось. Правило знаков. Определение силы по ее проекциям.

Проекция силы на ось – взятый со знаком + или – отрезок оси, заключенный между двумя перпендикулярными опущенными из начала и конца силы на ось.

Проекция силы на ось это скалярная алгебраическая величина.

Проекция силы на ось положительная при одинаковом направлении вектора силы и оси и отрицательная при противоположном направлении вектора силы и оси.

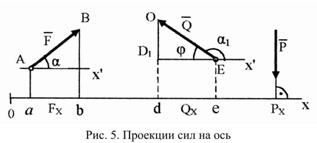
Проекция силы на ось это произвольная модуля силы на соS угла между силой и полож. направлением оси.

Модуль силы определяется по теореме Пифагора

Направление силы F определяется при помощи направляющих косинусов. Это cos угла между вектором силы и положительным направлением оси. (5)

Теорема о проекции геометрической суммы векторов на ось.

Проекция геом. Суммы векторов на какую либо ось равна алгебраической сумме проекций, составляющих сил (векторов) на ту же ось.

Из теоремы следует, что проекция равнодействующей системы сходящихся сил на какую либо ось равна алгебраической сумме проекций, составляющих сил на ту же ось.

Аналитическое определение равнодействующей плоской системы сходящихся сил.

Система сходящихся сил (ССС) – это система, образованная силами, линии действия которых пересекаются в одной точке (рис. 1.1).

ССС эквивалентна одной силе, которая равна геометрической сумме всех сил, входящих в эту систему, и проходит через точку пересечения этих сил. Эта сила называется - равнодействующей данной ССС или главным вектором. Систему сил, изображённую на (рис 1.1), можно заменить эквивалентной системой, где силы F1, F2, F3, F4 перенесены вдоль линии их действия в точку О пересечения этих линий (рис. 1.2). Сложить силы геометрически можно, используя способ построения силового многоугольника (рис. 1.3) или последовательных параллелограммов. При построении силового многоугольника каждый последующий вектор откладывается от конца предыдущего. Вектор силы, соединяющий начало первой отложенной силы с концом последней, является вектором равнодействующей силы R.

Так как данный способ является графическим, то для его реализации необходимо задать масштабный коэффициент F для изображения векторов сил. Длина вектора силы Fi на плане определится по формуле:

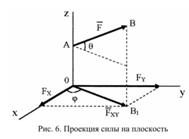
Аналитический способ задания силы. Для задания силы аналитическим способом необходимо выбрать систему координатных осей Охуz, по отношению к которой будет определяться направление силы в пространстве и задать отдельно точку приложения силы А ее координатами x, у, z. Для решения задач механики удобнее задавать силу ее проекциями Fx, Fy, Fz на координатные оси (рис. 6). Зная эти проекции, можно определить модуль силы F и углы α, β, γ, которые она образует с координатными осями Оx, Оу, Оz, по формулам:

Способы сложения и разложения сил.Величину, равную геометрической сумме сил системы, называют главным вектором этой системысил. Это понятие не следует отожествлять с понятием о равнодействующей.

1. Сложение двух сил. Геометрическая сумма R двух сил F1 и F2 , находится по правилу параллелограмма (рис. 7, а) или построением силового треугольника (рис. 7, б). Если угол между силами равен , то модуль R определяется по формулам:

2. Сложение системы сил. Геометрическая сумма (главный вектор) любой системы сил (рис..9, а) определяется построением силового многоугольника. Для этого откладываем от произвольной тючки О (рис. 9, б) вектор Oa , изображающий в выбранном масштабе силу F1 , от точки а — вектор ab , изображающий силу F2 , и т. д. Соединяя начало первого вектора с концом последнего, получаем вектор On= R изображающий геометрическую сумму или главный вектор слагаемых сил:

9. Геометрическое и аналитическое условие равнодействующей плоской системы сходящихся сил.

Геометрическое условие равновесия. ССС уравновешена, когда силовой многоугольник замкнут. Чтобы уравновесить ССС, изображенную на (рис. 1.2), надо добавить к ней силу Fур, равную по величине равнодействующей, но противоположную ей по направлению (рис. 1.3). Сила которая уравновешивает данную ССС, называется уравновешивающей.

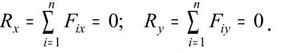
Аналитическое условие равновесия. Плоская ССС уравновешена, когда суммы проекций всех сил на каждую из двух координатных осей равны нулю:

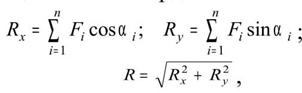
Для определения равнодействующей плоской ССС можно использовать метод сложения проекции сил на координатные оси:

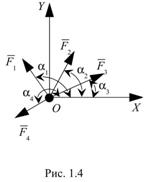
где ai ─ угол между положительным направлением оси x и направлением силы Fi (рис. 1.4).

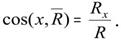
Направление равнодействующей R определится направляющим косинусом:

Пара сил. Момент пары сил.

Парой сил называется система двух равных по модулю, параллельных и направленных в противоположные стороны сил, действующих на абсолютно твердое тело (рис. 12, а). Плоскость, проходящая через линии действия сил пары, называется плоскостью действия пары. Кратчайшее расстояние d между линиями действия сил пары называется плечом пары. Действие пары сил на твердое тело сводится к вращательному эффекту и характеризуется моментом пары.

Векторный момент пары сил. Момент пары сил - это вектор М , модуль которого равен произведению модуля одной из сил пары на ее плечо (М = ±Fd) и который направлен перпендикулярно плоскости действия пары в ту сторону, откуда пара видна стремящейся повернуть тело против хода часовой стрелки. Но, в отличие от момента силы вектор m , как будет показано ниже, может быть приложен в любой точке (такой вектор называется свободным).

Момент пары сил относительно точки равен взятому с соответствующим знаком произведению модуля одной из сил пары на плечо пары: M₀(F) = ±F a

Точка О, относительно которой берется момент силы, называется центром момента.

Плечо силы(а) –это перпендикуляр, опущенный из центра момента (точка О) на линию действия сил.

Момент силы относительно точки – является скалярной алгебраической величиной.

Правило знаков такое же, что и для момента силы относительно центра.

Измеряется момент пары, как и момент силы, в ньютон -метрах.

Свойства момента силы относительно точки:

1.Момент силы относительно данной точки не меняется при переносе силы вдоль её линии действия, так как при этом не изменяется ни модуль силы, ни её плечо.

2. Момент силы относительно данной точки равен нулю, если линия действия силы проходит через эту точку, так как в этом случае плечо силы равно нулю: а=0

Свойства пар сил.

1.Теорема 1: алгебраическая сумма моментов сил пары относительно любой точки в плоскости действия этой пары- величина постоянная для данной пары и равна её моменту.

2. Пару сил можно перемещать в плоскости её действия.

3. У данной пары можно произвольно менять модули сил и длину плеча, сохраняя неизменным их произведение, т.е. момент.

4. Теорема2. Эквивалентность пар сил: две пары сил, имеющие равные моменты, эквивалентны, т.е. оказывают на тело одинаковое действие.

© 2014-2022 — Студопедия.Нет — Информационный студенческий ресурс. Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав (0.006)

Если к твердому телу приложены три сходящиеся силы, не лежащие в одной плоскости, то их равнодействующая приложена в точке пересечения линий действия сил и изображается диагональю параллелепипеда, построенного на этих силах (рис. 2.9).

Правило сложения трех сходящихся сил в пространстве называется правилом параллелепипеда сил.

Сходящиеся силы уравновешиваются в случае, если их равнодействующая равна нулю, т.е. многоугольник сил замкнут(рис. 2.10):

В замкнутом многоугольнике сил все силы направлены по контуру многоугольника в одну сторону по обходу многоугольника.

Аналитическая форма

Равнодействующая сходящихся сил (рис. 2.11) равна геометрической сумме этих сил:

Проекция равнодействующей на каждую из координатных осей равна алгебраической сумме проекций всех составляющих:

здесь проекции сил вычисляются по формулам:

Формулам (3) можно придать вид

причем i=1,2,…,n.

Вычислив проекции равнодействующей X, У и Z, найдем модуль и направление равнодействующей по формулам (2.8) и (2.9):

Если силы взаимно уравновешиваются, их равнодействующая равна нулю.

Для сходящихся сил в пространстве имеем следующие три уравнения равновесия:

Для сходящихся сил, расположенных в одной плоскости, получаем два уравнения равновесия:

Теорема о трех непараллельных силах

Правило сложения трех сходящихся сил в пространстве называется правилом параллелепипеда сил.

Аналитическая форма

Равнодействующая сходящихся сил (рис. 2.11) равна геометрической сумме этих сил:

здесь проекции сил вычисляются по формулам:

Формулам (3) можно придать вид

причем i=1,2,…,n.

Если силы взаимно уравновешиваются, их равнодействующая равна нулю.

Для сходящихся сил в пространстве имеем следующие три уравнения равновесия:

Для сходящихся сил, расположенных в одной плоскости, получаем два уравнения равновесия:

Системой сходящихся сил называют группу двух, трех и более сил, приложенных к телу, линии действия которых пересекаются в некоторой точке.

Пусть, к абсолютно твердому телу приложена система N сил (F₁, F₂, … F_N), расположенных в пространстве так, что их линии действия пересекаются в одной точке О (рисунок 1).

Такую систему сил называют системой сходящихся сил. Упростим систему сходящихся сил, т.е. решим первую задачу статики.

Приведение к равнодействующей

Докажем, что данная система сил эквивалентна одной силе, т.е. приводится к равнодействующей силе.

В самом деле, так как сила есть вектор скользящий, то все силы данной системы можно перенести вдоль линий их действия в точку О.

Далее, по четвертой аксиоме, силы F₁ и F₂ можно заменить их равнодействующей R_1,2 (рисунок 1), которая определяется диагональю параллелограмма, построенного на этих силах как на сторонах, и направленной по этой диагонали, т.е.

Далее можно записать аналогичные соотношения для полученной равнодействующей силы R * _1,2 и силы F₃, тогда

Для системы N сил окончательно будем иметь

На рисунке 2, a показано построение равнодействующей указанным способом на примере системы, состоящей из четырех сил. Однако процесс определения равнодействующей удобнее вести иным путем, с помощью построения так называемого силового многоугольника.

Силовой многоугольник

Из конца вектора силы F₁ (точки В) проводим вектор ВС, геометрически равный силе F₂. Из конца этого вектора (точки С) проводим вектор СD равный силе F₃. Из конца этого вектора (точки D) проводим вектор DE, равный силе F₄.

Полученный многоугольник ABCDE называется силовым многоугольником. Процесс его построения хорошо виден на рисунке 2, б. Стороны силового многоугольника называются составляющими силами.

Вектор АЕ, соединяющий начало А первой силы с концом Е последней силы и направленный навстречу составляющим силам, называется замыкающей стороной силового многоугольника.

Следовательно, равнодействующая системы сходящихся сил изображается в выбранном масштабе замыкающей силового многоугольника, построенного на составляющих силах.

Нахождение равнодействующей системы сходящихся сил по правилу силового многоугольника называется векторным или геометрическим сложением сил.

Таким образом, мы доказали, что система сходящихся сил в общем случае эквивалентна одной силе, т.е. равнодействующей, которая приложена в точке пересечения линий действия всех сил и равна их геометрической сумме.

Вычисление равнодействующей

Для аналитического определения равнодействующей найдем ее проекции R_x, R_y, R_z на оси декартовой системы координат. Имеем

Тогда величина равнодействующей определится следующей формулой:

Для определения направления равнодействующей R* воспользуемся обычными выражениями для направляющих косинусов:

Здесь α , β , γ — углы между положительным направлением осей координат и равнодействующей.

Равенства (2)-(5) позволяют определить модуль и направление равнодействующей по заданным проекциям составляющих сил.

В случае плоской системы сходящихся сил оси координат можно взять в плоскости действия сил и тогда формулы (2)-(5) упрощаются.

Равнодействующая системы сходящихся сил приложена в точке пересечения линий действия всех сил и равна их геометрической сумме.

Система сходящихся сил

Приведение к равнодействующей

Докажем, что данная система сил эквивалентна одной силе, т.е. приводится к равнодействующей силе.

Далее можно записать аналогичные соотношения для полученной равнодействующей силы R * _1,2 и силы F₃, тогда

Для системы N сил окончательно будем иметь

Силовой многоугольник

Вычисление равнодействующей

Тогда величина равнодействующей определится следующей формулой:

Здесь α , β , γ — углы между положительным направлением осей координат и равнодействующей.

Законы сложения сил в механике

При воздействии на одно тело нескольких сил одновременно тело начинает двигаться с ускорением, являющимся векторной суммой ускорений, которые бы возникли под воздействием каждой силы по отдельности. К действующим на тело силам, приложенным к одной точке, применяется правило сложения векторов.

Векторная сумма всех сил, одновременно воздействующих на тело, это сила равнодействующая, которая определяется по правилу векторного сложения сил:

R → = F 1 → + F 2 → + F 3 → + . . . + F n → = ∑ i = 1 n F i → .

Равнодействующая сила действует на тело также, как и сумма всех действующих на него сил.

Правило параллелограмма и правило многоугольника

Для сложения 2 -х сил используют правило параллелограмма (рисунок 1 ).

Рисунок 1 . Сложение 2 -х сил по правилу параллелограмма

Выведем формулу модуля равнодействующей силы с помощью теоремы косинусов:

R → = F 1 → 2 + F 2 → 2 + 2 F 1 → 2 F 2 → 2 cos α

При необходимости сложения более 2 -х сил используют правило многоугольника: от конца
1 -й силы необходимо провести вектор, равный и параллельный 2 -й силе; от конца 2 -й силы необходимо провести вектор, равный и параллельный 3 -й силе и т.д.

Рисунок 2 . Сложение сил правилом многоугольника

Конечный вектор, проведенный от точки приложения сил в конец последней силы, по величине и направлению равняется равнодействующей силе. Рисунок 2 наглядно иллюстрирует пример нахождения равнодействующей сил из 4 -х сил: F 1 → , F 2 → , F 3 → , F 4 → . Причем суммируемые векторы совсем необязательно должны быть в одной плоскости.

Результат действия силы на материальную точку будет зависеть только от ее модуля и направления. У твердого тела есть определенные размеры. Потому силы с одинаковыми модулями и направлениями вызывают разные движения твердого тела в зависимости от точки приложения.

Линией действия силы называют прямую, проходящую через вектор силы.

Рисунок 3 . Сложение сил, приложенных к различным точкам тела

Если силы приложены к различным точкам тела и действуют не параллельно по отношению друг к другу, тогда равнодействующая приложена к точке пересечения линий действия сил (рисунок 3 ). Точка будет находиться в равновесии, если векторная сумма всех сил, действующих на нее, равняется 0 : ∑ i = 1 n F i → = 0 → . В данном случае равняется 0 и сумма проекций данных сил на любую координатную ось.

Разложение вектора силы по направлениям

Разложение сил на две составляющие – это замена одной силы 2 -мя, приложенными в той же точке и производящими на тело такое же действие, как и эта одна сила. Разложение сил осуществляется, как и сложение, правилом параллелограмма.

Задача разложения одной силы (модуль и направление которой заданы) на 2 , приложенные в одной точке и действующие под углом друг к другу, имеет однозначное решение в следующих случаях, когда известны:

направления 2 -х составляющих сил;
модуль и направление одной из составляющих сил;
модули 2 -х составляющих сил.

Необходимо разложить силу F на 2 составляющие, находящиеся в одной плоскости с F и направленные вдоль прямых a и b (рисунок 4 ). Тогда достаточно от конца вектора F провести 2 прямые, параллельные прямым a и b . Отрезок F A и отрезок F B изображают искомые силы.

Рисунок 4 . Разложение вектора силы по направлениям

Второй вариант данной задачи – найти одну из проекций вектора силы по заданным векторам силы и 2 -й проекции (рисунок 5 а ).

Рисунок 5 . Нахождение проекции вектора силы по заданным векторам

Во втором варианте задачи необходимо построить параллелограмм по диагонали и одной из сторон, как в планиметрии. На рисунке 5 б изображен такой параллелограмм и обозначена искомая составляющая F 2 → силы F → .

Итак, 2 -й способ решения: прибавим к силе силу, равную — F 1 → (рисунок 5 в ). В итоге получаем искомую силу F → .

Три силы F 1 → = 1 Н ; F 2 → = 2 Н ; F 3 → = 3 Н приложены к одной точке, находятся в одной плоскости (рисунок 6 а ) и составляют углы с горизонталью α = 0 ° ; β = 60 ° ; γ = 30 ° соответственно. Необходимо найти равнодействующую силу.

Решение

Рисунок 6 . Нахождение равнодействующей силы по заданным векторам

Нарисуем взаимно перпендикулярные оси О Х и O Y таким образом, чтобы ось О Х совпадала с горизонталью, вдоль которой направлена сила F 1 → . Сделаем проекцию данных сил на координатные оси (рисунок 6 б ). Проекции F 2 y и F 2 x отрицательны. Сумма проекций сил на координатную ось О Х равняется проекции на данную ось равнодействующей: F 1 + F 2 cos β — F 3 cos γ = F x = 4 — 3 3 2 ≈ — 0 , 6 Н .

Точно также для проекций на ось O Y : — F 2 sin β + F 3 sin γ = F y = 3 — 2 3 2 ≈ — 0 , 2 Н .

Модуль равнодействующей определим с помощью теоремы Пифагора:

F = F x 2 + F y 2 = 0 , 36 + 0 , 04 ≈ 0 , 64 Н .

Направление равнодействующей найдем при помощи угла между равнодействующей и осью (рисунок 6 в ):

t g φ = F y F x = 3 — 2 3 4 — 3 3 ≈ 0 , 4 .

Сила F = 1 к Н приложена в точке В кронштейна и направлена вертикально вниз (рисунок 7 а ). Необходимо найти составляющие данной силы по направлениям стержней кронштейна. Все необходимые данные отображены на рисунке.

Решение

Рисунок 7 . Нахождение составляющих силы F по направлениям стержней кронштейна

Дано:

F = 1 к Н = 1000 Н

Пускай стержни прикручены к стене в точках А и С . На рисунке 7 б изображено разложение силы F → на составляющие вдоль направлений А В и В С . Отсюда понятно, что

F 1 → = F t g β ≈ 577 Н ;

F 2 → = F cos β ≈ 1155 Н .

Ответ: F 1 → = 557 Н ; F 2 → = 1155 Н .

ПроСопромат.ру

Технический портал, посвященный Сопромату и истории его создания

Задача

Укажите, какой вектор силового многоугольника является равнодействующей силой:

Равнодействующая сила в силовом многоугольнике всегда направлена от начала первого слагаемого вектора к концу последнего. Так как векторы ОА, АВ, ВС,СD направлены последовательно один за другим, то ни один из них не может быть равнодействующей силой.

Равнодействующей силой является вектор ОD.

Читайте также: