Формула тейлора доказательство кратко

Обновлено: 05.07.2024

Формула Тейлора с остаточным членом в форме Лагранжа.

Если функция $f(x)$ имеет в точке $x_$ производную n-го порядка, то существует многочлен $P_(x)$ степени не выше n такой, что
$$
P_n(x_0)=f(x_),\ P_^(x_)=f^(x_),\ k=\overline.\label
$$
Этот многочлен представляется в виде
$$
P_n(x)=f(x_)+\frac(x-x_0)+\frac(x-x_0)^2+\ldots+\frac(x_0)>(x-x_0)^n.\label
$$

$\circ$ Пусть $\varphi(x)=(x-x_0)^m$, где $m\in\mathbb$. Тогда $\varphi(x_0)=0$,
$$
\varphi^(x_)=\left\
0, & если \ k\neq m,\\
k!, & если \ k=m.
\end\right.\label
$$
Из \eqref следует, что многочлен $P_n(x)$, заданный формулой \eqref, удовлетворяет условиям \eqref. Этот многочлен называют многочленом Тейлора n-го порядка для функции $f(x)$ в точке $x_$. $\bullet$

Пусть функции $f(x)$ и $\psi(x)$ определены в $\delta$-окрестности точки $x_0$ и удовлетворяют следующим условиям:

для каждого $x\in U_(x_0)$ существуют $\varphi^(x)$ и $\psi^$;
$$
\begin
\varphi(x_0)=\varphi'(x_0)=\ldots=\varphi^(x_0)=0,\\
\psi(x_0)=\psi'(x_0)=\ldots=\psi^(x_0)=0;
\end\label
$$
$\psi(x)\neq 0$, $\psi^(x)\neq 0$ для $x\in \dot_(x_)$ и для $k=\overline$.

Тогда для каждого $x\in\dot_(x_)$ существует точка $\xi$, принадлежащая интервалу с концами $x_0$ и $x$ такая, что
$$
\frac<\psi(x)>=\frac(\xi)><\psi^<(n+1)>(\xi)>.\label
$$

$\circ$ Пусть, например, $x\in(x_0,x_0+\delta)$. Тогда, применяя к функциям $\varphi$ и $\psi$ на отрезке $[x_0,x]$ теорему Коши и учитывая, что $\varphi(x_0)=\psi(x_0)=0$ в силу условий \eqref, получаем
$$
\frac<\psi(x)>=\frac<\psi(x)-\psi(x_0)>=\frac<\varphi'(\xi_1)><\psi'(\xi_1)>\quad x_0 Теорема 1.

Пусть существует $\delta >0$ такое, что функция $f(x)$ имеет в $\delta$-окрестности точки $x_0$ производные до $(n+1)$-го порядка включительно.

Тогда для любого $x\in\dot_\delta(x_0)$ найдется точка $\xi$, принадлежащая интервалу $\Delta$ с концами $x_$ и $x$, такая, что
$$
f(x)=f(x_0)+\frac(x-x_0)+\ldots+\frac(x_)>(x-x_0)^n+\frac(\xi)>(x-x_)^.\label
$$

$\circ$ Пусть $x\in\dot_\delta(x_0)$, $P_n(x)=\displaystyle \sum_^\frac(x_)>(x-x_0)^k$ — многочлен Тейлора для функции $f(x)$. Обозначим
$$
r_(x)=f(x)-P_n(x).\label
$$
Так как многочлен $P_(x)$ удовлетворяет в силу леммы 1 условиям \eqref, то из равенства \eqref следует, что
$$
r_n(x_0)=r_n'(x_0)=\ldots=r_^(x_)=0.\label
$$
Рассмотрим функции $\varphi(x)=r_n(x)$, $\psi(x)=(x-x_0)^$. Эти функции удовлетворяют условиям леммы 2, и поэтому для них выполняется равенство \eqref, то есть
$$
\frac<\psi(x)>=\frac<(x-x_0)^>=\frac(\xi)>=\frac(\xi)>,\quad\xi\in\Delta,\label
$$
так как $P_n^(x)\equiv 0,\ \psi^(x)=(n+1)!$ Из равенств \eqref и \eqref следует формула \eqref. $\bullet$

Функцию $r_n(x)=\displaystyle \frac(\xi)>(x-x_0)^$ называют остаточным членом формулы Тейлора в форме Лагранжа. Формула \eqref справедлива и при $x=x_$.

Если функции $\varphi$ и $\psi$ дифференцируемы $n$ раз при $x\geq x_$ и удовлетворяют условиям $\varphi^(x_)=\psi^(x_)$, $k=\overline$, $\varphi^(x)>\psi^(x)$ при $x > x_0$, то $\varphi(x) > \psi(x)$ при $x > x_$.

$\circ$ Для $n=1$ утверждение доказано ранее (следствие 4 из теоремы Лагранжа). Обозначим $f(x)=\varphi(x)-\psi(x)$. Тогда $f^(x_)=0$ при $k=\overline0$, и по формуле \eqref получаем
$$
f(x)=\frac(x-x_)^f^(\xi).\nonumber
$$
Если $ x> x_$, то $\xi > x_0$, $f^(\xi)=\varphi^(\xi)-\psi^(\xi) > 0$, и поэтому $f(x) > 0$, то есть $\varphi(x) > \psi(x)$ при $x > x_$. $\bullet$

$|\sin t-t|\leq\displaystyle\frac$ для $t\in\mathbb$;
$$
x-\frac>0.\label
$$

$\triangle$ Применяя формулу \eqref при $n=2$ и $x_0=0$ к функции $f(t)=\sin t$, получаем $\sin t=t-\displaystyle\frac<\sin<\xi>>t^2$, откуда следует, что $|\displaystyle \sin t-t|\leq\frac>,\;t\in\mathbb$.
Если $f(x)=\sin x$, то $f(0)=f^(0)=f^(0)=0$, $f'(0)=1,\ f^(0)=-1$, $f^(x)=(\sin x)^=\displaystyle\sin\left(x+n\frac<\pi>\right)$. Применяя формулу \eqref при $n=5$, $x_0=0$, получаем
$$
\sin x=x-\frac>+\frac>\sin(\xi+5\frac<\pi>),\nonumber
$$
откуда следует правое неравенство \eqref, так как, очевидно, $\left|\displaystyle \frac>\sin\left(\xi+5\frac<\pi>\right)\right|\leq\displaystyle\frac>$ при $x >0$. Используя формулу \eqref для $f(x)=\sin x$ при $n=3$, $x_0=0$, докажем левое неравенство \eqref. $\blacktriangle$

Формула Тейлора с остаточным членом в форме Пеано.

Из существования $f^(x_0)$ следует, что функция $f(x)$ определена и имеет производные до $(n-1)$-го порядка включительно в $\delta$-окрестности точки $x_0$. Обозначим $\varphi(x)=r_n(x)$, $\psi(x)=(x-x_0)^n$, где функция $r_n(x)$ определяется формулой \eqref. Функции $\varphi(x)$ и $\psi(x)$ удовлетворяют условиям леммы 2, если заменить номер $n+1$ на номер $n-1$ (см. равенства \eqref). Используя лемму 2 и учитывая, что $r_n^(x_0)=0$, получаем
$$
\frac=\frac)>,\label
$$
где $\xi=\xi(x)$ и
$$
x_0 Замечание 2.

Формулу \eqref часто называют формулой Тейлора с остаточным членом в форме Пеано или локальной формулой Тейлора.

Разложить функцию $f(x)$ по формуле Тейлора в окрестности точки $x_0$ до $o((x-x_0)^n)$ — значит представить ее в виде \eqref.

$\circ$ По теореме 2 справедлива формула \eqref, и так как по условию выполняется равенство \eqref, то
$$
a_0+a_1(x-x_0)+\ldots+a_n(x-x_0)^n+o((x-x_0)^n)=\\=f(x_)+f'(x_)(x-x_0)+\ldots+f^(x_)\frac<(x-x_)^>+o((x-x_0)^n).\label
$$
Переходя к пределу при $x\rightarrow x_$ в равенстве \eqref, получаем $a_=f(x_)$. Отбросив в левой и правой частях этого равенства одинаковые слагаемые $a_$ и $f(x_)$ и разделив обе части полученного равенства на $x-x_0$, имеем
$$
a_1+a_2(x-x_0)+\ldots+a_n(x-x_0)^+o((x-x_0)^)=\\=f'(x_0)+\frac(x-x_0)+\ldots+\frac(x-x_0)^+o((x-x_0)^).
$$
Переходя в этом равенстве к пределу при $x\rightarrow x_0$, находим $f'(x_)=a_$. Продолжая эти рассуждения, получаем равенства \eqref. $\bullet$

Теорема 3 означает, что представление в виде \eqref функции, имеющей в точке $x_$ производную $n$-го порядка, единственно: коэффициенты разложения \eqref выражаются по формулам \eqref.

Разложить функцию $\displaystyle \frac$ по формуле Тейлора в окрестности точки $x_=0$ до $o(x^)$.

$\triangle$ Воспользуемся равенством $(1+x+\ldots+x^)(1-x)=1-x^$, откуда $\displaystyle \frac=1+x+\ldots+x^n+r_n(x)$, где $r_n(x)=\displaystyle \frac=o(x^)$ при $x\rightarrow 0$. Таким образом,
$$
\frac=1+x+\ldots+x^n+o(x^n).\label
$$
Так как функция $\displaystyle \frac$ бесконечно дифференцируема при $x\neq 1$ (имеет производные любого порядка), то по теореме 3 формула \eqref дает искомое разложение. $\blacktriangle$

Разложение основных элементарных функций по формуле Тейлора.

Если $x_=0$ и существует $f^(0)$, то равенство \eqref принимает вид
$$
f(x)=\sum_^\frac>x^k+o(x^n),\ x\rightarrow 0.\label
$$
Формулу \eqref называют формулой Маклорена.

Пусть, функция $f(x)$ бесконечно дифференцируема на интервале $(-l,l)$. Если эта функция является четной, то ее производная — нечетная функция, и, наоборот, производная нечетной функции — четная функция (мы уже разбирали этот пример). Отсюда следует, что для нечетной функции $f$ выполняются условия $f^(0)=0$, $k\in\mathbb$, а для четной функции $f$ — условия $f^(0)=0$, $k\in\mathbb$, так как любая непрерывная нечетная функция принимает при $x=0$ значение нуль.

Поэтому формулу \eqref для бесконечно дифференцируемой четной функции можно записать в виде
$$
f(x)=\sum_^\frac(0)>x^+o(x^),\quad x\rightarrow 0,\label
$$
а для нечетной функции — в виде
$$
f(x)=\sum_^\frac(0)>x^+o(x^),\quad x\rightarrow 0,\label
$$
В формуле \eqref остаточный член записан в виде $o(x^)$, а не в виде $о(x^)$, так как для четной функции $f$ выполняется условие $f^(0)=0$, и поэтому член многочлена Тейлора, который следует за слагаемым $\displaystyle\frac(0)>x^$ равен нулю. Аналогично рассматривается вопрос о записи остаточного члена формулы \eqref.

Показательная функция.

Гиперболические функции.

Так как $\operatornamex=\displaystyle \frac-e^>$, $\operatornamex=\displaystyle \frac+e^>$, то формулы \eqref и \eqref можно получить, используя равенство \eqref и равенство $e^=\displaystyle \sum_^\fracx^>+о(x^),\ x\rightarrow 0$.

Используемая в математике формула Тейлора предназначена для поэтапного разложения функции в бесконечную сумму степенных значений. Достижения талантливого учёного были доступны ещё до официальной публикации. Ряд Тейлора был востребован в Индии в середине XIV века. Описываемая формула активно использовалась при аппроксимации функции многочленами. Качественная линеаризация конкретных уравнений может быть выполнена только в результате разложения в ряд Тейлора.

Краткое описание
Ключевые особенности
Аналогичность функций
Практическое применение
Основные примеры
Интересные факты

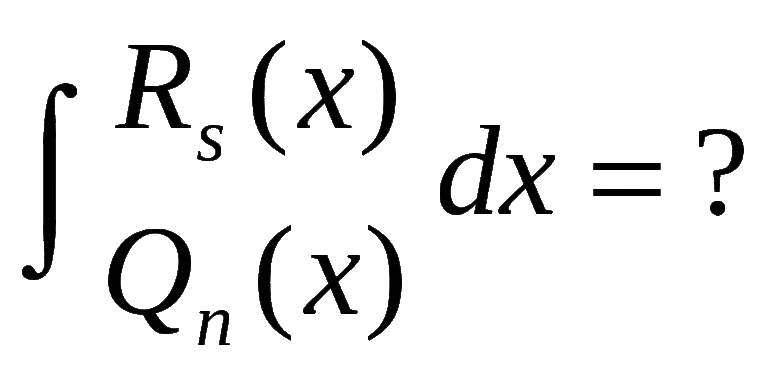
Краткое описание

Существует теория приближения функций, которая на практике является неотъемлемым элементом математики. Для подробного изучения этой темы крайне важно понимать, что под приближением функции подразумевают замену по действующим нормам одной функции другой, которая максимально приближена к исходным данным в том или ином смысле. Необходимость выполнять перечисленные действия возникает в том случае, когда конкретную функцию нужно заменить на более простую и понятную для всех дальнейших математических расчётов.

Применение формулы Тейлора в онлайн-режиме пользуется большим спросом, так как в этом случае можно избежать грубых ошибок. Это математическое направление активно используется для поэтапного разложения функций в степенной ряд Фурье. Но некоторые трудности могут возникнуть на этапе вычисления интегралов. Существенно упростить поставленную задачу позволяет только замена данных степенным рядом.

Правильное нахождение показателей стандартных и обратных тригонометрических, а также логарифмических функций может быть сведено к нахождению значений соответствующих многочленов. Классический метод решения поставленных задач подразумевает предварительное изучение всех правил и математических примеров.

Ключевые особенности

К настоящему моменту изложено достаточно много частей дифференциального исчисления, но практически у всех учеников возникает верное представление о том, что чем больше присутствует производных, которые совпадают в определённой точке сразу у двух функций, тем лучше они аппроксимируют друг друга в окрестностях этой точки. Особым спросом пользуется приближение функции в пределах конкретной точки с помощью элементарного многочлена: Bn (x) = Bn (x0; x) = s0+s1 (x—x0) +…+ Sn (x—x0) n .

Элементарная функция d (x) обладает всеми необходимыми производными до n+1. Если функцию или корень квадратный можно разложить в ряд Тейлора в некоторой нулевой точке, то предварительно нужно удостовериться в том, что функция является аналитической в конкретной точке. В противном случае получится самый обычный ряд, который не равен своей функции. Ряд Тейлора можно с уверенностью назвать степенным рядом, так как он имеет в качестве области сходимости круг для случая комплексной переменной, а также обычный интервал для вещественной переменной.

Используемые сегодня математические формулы являются плодом многолетних трудов учёного, а вот современным людям остаётся только отыскать в многочисленных комбинациях ту, которая максимально подойдёт для конкретной ситуации. Математика считается той наукой, которая кажется незаметной, но она сопровождает человека в течение всей его жизни. В процессе естественной эволюции формула Маклорена (Тейлора) была подвержена незначительным изменениям, а связано это с изменением понимания назначения самой формулы.

Чтобы получить наиболее точное значение функции при наименьшем количестве членов разложения, надо в качестве параметра А выбрать такое число, которое достаточно близко к значению х, и значение функции от этого числа легко вычисляется. К примеру, нужно правильно вычислить значение sin20 0 . Предварительно нужно перевести имеющееся значение в радианы.

В четырёхзначных таблицах Брадиса для существующего синуса этого угла указано значение 0,3420. Большим спросом также пользуется расширенный список эквивалентности элементарных функций. На элементарном графике можно отобразить изменение значений разложения в ряд (в зависимости от реального количества членов разложения). Если ограничится только тремя членами разложения, то в итоге будет достигнуто значение 0,0002.

Аналогичность функций

Основные примеры формулы Тейлора позволяют учащимся разобраться во всех нюансах, без которых правильно решить задачу просто невозможно. Стоит представить некоторую функцию h (x), которую нужно правильно разложить в ряд х = b. Нужно убедиться, что функция является аналитической. На примере функции Коши можно увидеть, что любая функция может быть дифференцируемой в точке b неограниченное количество раз. Ряд Тейлора с параметром b может быть сходящимся, но при этом итог часто не соответствует своей функции.

Обязательным условием аналитичности функции всегда считается сходимость ряда Тейлора в определённой непрерывной области. Если ряд сходится исключительно в одной точке, то она будет равна формуле х = b. Но в такой ситуации сформированный ряд будет соответствовать функции h (x) только в конкретной точке. Полученный результат будет служить подтверждением того, что функция не будет аналитической.

Экспертами доказано, что в ряд Тейлора с остаточным членом может быть разложена абсолютно любая функция, которая в окрестности точки b до бесконечности дифференцируется. Если был задан предел для каждой из двух существующих последовательностей, то итоговый результат будет равен сумме этих же пределов.

В такой ситуации данные для всех неизвестных из окрестности b по формуле Тейлора примут весьма непредвиденный вид. Логически можно отметить тот факт, что функция h (x) является аналитической в точке b исключительно в том случае, если в описанной окрестности точки b была выявлена непрерывная область Х. Остаточный член разложения по формуле Тейлора стремится к абсолютному нулю с ростом m. Для более результативного изучения этой темы следует рассмотреть экспоненциальную функцию g x .

Ряд Тейлора сходится по всей оси х для любых параметров b. При помощи математических приёмов ученику необходимо доказать аналитичность функции во всех точках b. Последние символы указывают на некоторое число, которое заключено между x и b. После всех выполненных манипуляций можно получить правильный результат.

Если всё проанализировать, то в итоге можно определить, что на фиксированном промежутке экспонента ограничена определённым числом М. А вот предел остаточного члена равен нулю для имеющихся x и b.

Практическое применение

Универсальная формула Тейлора для функции нескольких переменных активно используется в математике. Талантливыми учёными было доказано, что для элементарной программы можно ограничиться шестью либо семью членами ряда для числа p в степени x, а также пятью членами ряда для логарифма натурального типа. Специалистам отлично известна связь формулы с десятичным логарифмом. Самостоятельное написание программы для вычисления десятичных логарифмов гораздо упрощается. Благодаря такому подходу можно в автоматическом режиме высчитать значение натурального логарифма, а потом получить достоверный результат в десятичном виде.

Многогранность формулы Тейлора для косинусов позволяет правильно разработать логическую структуру программы. Вложенные циклы используются для большей наглядности, что существенно упрощает эксплуатацию. Программа построена таким образом, что пользователю необходимо ввести только правильный номер требуемой функции и аргумент x для конкретной функции.

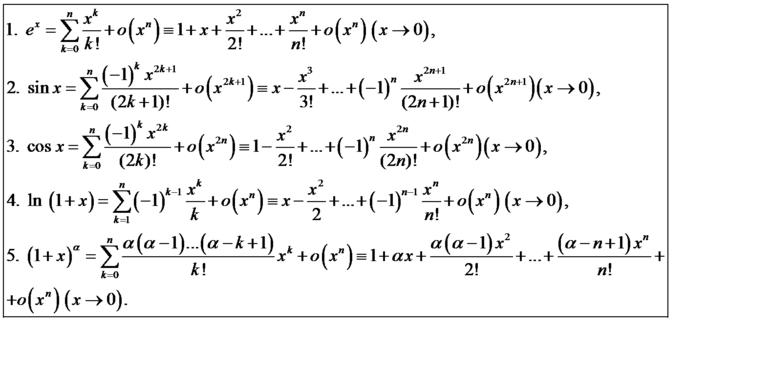
На финальном этапе разработки универсальной программы происходит перевод результатов из экспоненциальной формы конкретного числа в наиболее привычную форму вещественного числа. Но даже в этом случае действуют свои правила. Программа имеет определённые ограничения в использовании, так как реальное значение функции и полученное автоматическим путём значение не сходится.

Даже самое тщательное разложение по формуле талантливого Тейлора с ограниченным рядом членов в итоге даёт минимальные погрешности при малых значениях аргумента. Для расширения возможностей программы следует существенно увеличить длину ряда. Аналогичный подход можно встретить в инновационных калькуляторах и ЭВМ. Большим спросом пользуется табличное разложение обычного тангенса и арктангенса.

Основные примеры

Элементарное доказательство формулы Тейлора позволяет решать даже самые сложные математические задачи. Достижения талантливого учёного используются при аппроксимации функции элементарными многочленами. Даже линеаризация уравнений может быть осуществлена путём разложения в ряд и последующего отсечения абсолютно всех существующих членов первого порядка. Изучаемая формула также активно используется при математическом доказательстве большого количества теорем в своеобразном дифференциальном исчислении.

В качестве примера следует разложить в ряд следующую функцию: l (x)=1/x. Следует учесть, что в окрестности точки x 0 приравнивается к единице. Для решения задачи следует задействовать замену:

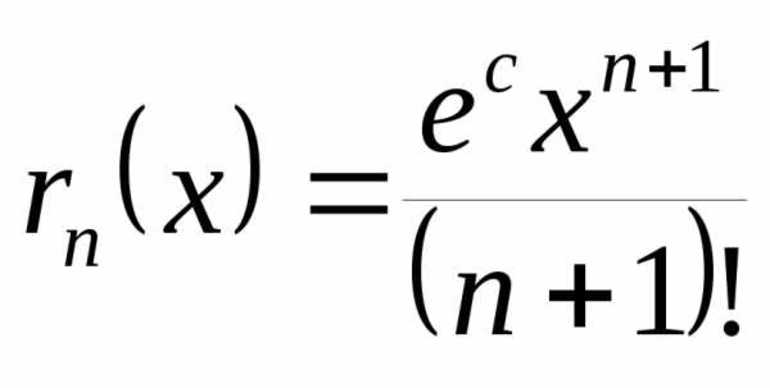
x—x0 = x — 1 = r.
Благодаря этому функция сводится к следующему виду: l (x)= l (r+1) = 1/1+ r.

Полученный результат лучшим образом демонстрирует разложение по степеням двучлена (х-1).

Многие спорные моменты также может разрешить следующий пример, в соответствии с которым происходит разложение математического уравнения d (x) = (x+1) tr (x2+2x+2). Окрестности точки х 0 = -1 с точностью до 0 ((х+1) 7 ).

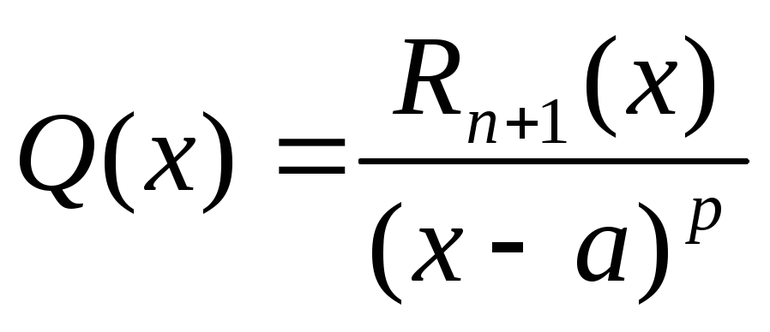
Если выполнить замену переменной, то в итоге можно получить следующий результат:

x-x 0 =x+1=q;
w (q)=qtr (1+q2);
q (w)=q (w2/1!)−(w 2 ) 2 /2!+(w 2 ) 3 /3!+o ((w 2 ) 3 )=w3−w 5 /2+w 7 /6+o (w 7 ).

На финальном этапе остаётся только выполнить обратную замену переменной. Правильное решение поставленной задачи выглядит следующим образом: d (x)=(x+1) 3 −(x+1) 5 /2+(x+1) 7 /6+o ((x+1) 7 ).

Интересные факты

Тейлор Брук был талантливым английским математиком, членом почётного Лондонского королевского общества. Благодаря своей целеустремлённости он получил общую формулу разложения функций в своеобразный степенной ряд. Тейлор также положил начало математическому изучению задачи о колебаниях струны. Этот математик является автором работ о полёте снарядов, тесном взаимодействии магнитов, центров качания. До своих последних дней Тейлор Брук усердно занимался изучением философских вопросов.

Но многие математики руководствовались исключительно своим опытом, из-за чего у них было большое сомнение по поводу того, что абсолютно любая непрерывная функция распадается в бесконечный ряд. Только в XIX веке Коши смог дать действительно интересный пример функции. Благодаря этому многие вспомнили, что именно Тейлор впервые разработал универсальные основы нормирования труда, а также смог внедрить в практику научные подходы к подбору квалифицированного персонала. Система Тейлора заложила основы научной организации труда через создание формул и законов.

Ряд Тейлора — разложение функции в бесконечную сумму Брука Тейлора .

$<\displaystyle f(x)> Пусть функция$
бесконечно дифференцируема в некоторой окрестности точки " width="" height="" />
, тогда ряд

$<\displaystyle f(x)=f(a)+\sum _<k=1> ^<\infty >(a) \over k!>(x-a)^>$

$<\displaystyle f> называется рядом Тейлора функции$
в точке " width="" height="" />
.

$<\displaystyle a=0> В случае, если$
, этот ряд иногда называется рядом Маклорена.

Если " width="" height="" />
есть аналитическая функция, то её ряд Тейлора в любой точке " width="" height="" />
области определения " width="" height="" />
сходится к " width="" height="" />
в некоторой окрестности " width="" height="" />
.

Содержание

Формула Тейлора

Формула Тейлора используется при доказательстве большого числа теорем в дифференциальном исчислении. Говоря нестрого, формула Тейлора показывает поведение функции в окрестности некоторой точки.

Это формула Тейлора с остаточным членом в общей форме (форме Шлемильха — Роша).

Различные формы остаточного члена

В форме

Ослабим предположения:

Интересные факты

Несмотря на то, что фамилия Тейлор правильно произносится с ударением на первом слоге, некоторые преподаватели старой закалки любят говорить Тейлóр и таким образом проверять кто же из студентов ходил на лекции, а кто нет. В некоторых случаях подобный трюк проделывают с фамилией Банаха.

Ряд назван в честь английского математика Тейлора, хотя ряд Тейлора был известен задолго до публикаций Тейлора — его использовали ещё в XVII веке Грегори, а также Ньютон.

Ряды Тейлора применяются при аппроксимации функции многочленами. В частности, линеаризация уравнений происходит путём разложения в ряд Тейлора и отсечения всех членов выше первого порядка.

Содержание

Определение

Пусть функция f(x) бесконечно дифференцируема в некоторой окрестности точки a . Формальный ряд

$\sum_<k=0> ^\infty (a) \over k!> (x - a)^k$

называется рядом Тейлора функции f в точке a .

Связанные определения

В случае, если a = 0 , этот ряд также называется рядом Макло́рена.

Свойства

$f(x)= \left\< \begin <ul> <li>Если f есть аналитическая функция, то её ряд Тейлора в любой точке a области определения f сходится к f в некоторой окрестности a .</li> <li>Существуют бесконечно дифференцируемые функции, ряд Тейлора которых сходится, но при этом отличается от функции в любой окрестности a . Например: 0,&\ \ x=0\\ e^ &\ \ x\not=0 \end \right.,\ \ a=0.$

Формула Тейлора

тогда: точка при x или при x > a :

$f(x) = f(a) + \sum_<k=1> ^n (a) \over k!> (x - a)^k + \left(\right)^p<(x - \xi)^<n+1>\over n! p>f^(\xi)$

Это формула Тейлора с остаточным членом в общей форме (форма Шлёмильха — Роша).

Различные формы остаточного члена

$R_<n+1> (x) = <(x - a)^<n+1>\over (n+1)!>f^ [a + \theta(x - a)] \qquad p = n+1$

$R_<n+1> (x) = <(x - a)^<n+1>(1 - \theta)^n \over n!>f^ [a + \theta(x - a)] \qquad p = 1$

Пусть функция f(x) имеет n − 1 производную в некоторой окрестности точки a
И n производную в самой точке a , тогда:

Ряды Маклорена некоторых функций

$\mathrm<e> ^ = 1 + x + \frac + \frac + \cdots = \sum^<\infin>_ \frac,\forall x$

+ \frac - \cdots = \sum^<\infin>_ \frac> = \sum^<\infin>_ \frac<(- 1)^x^n>," width="" height="" />
для всех

_ x^n," width="" height="" />
для всех и всех комплексных где

$<\alpha\choose n> = \prod_^n \frack = \frac\! = \frac\!$

+ \frac - \cdots\ = \sum^<\infin>_ \frac x^,\forall x" width="" height="" />
+ \frac - \cdots = \sum^<\infin>_ \frac x^,\forall x" width="" height="" />
x = x + \frac + \frac + \cdots = \sum^<\infin>_ \frac x^," width="" height="" />
для всех " width="" height="" />
_ \frac<(-1)^n E_> x^" width="" height="" />
для всех " width="" height="" />
_ \frac x^" width="" height="" />
для всех x = \sum^<\infin>_ \frac x^" width="" height="" />
для всех

\left(x\right) = x + \frac + \frac + \cdots = \sum^<\infin>_ \frac x^,\forall x" width="" height="" />
\left(x\right) = 1 + \frac + \frac + \cdots = \sum^<\infin>_ \frac x^,\forall x" width="" height="" />
\left(x\right) = \sum^<\infin>_ \frac x^" width="" height="" />
для всех " width="" height="" />
\left(x\right) = \sum^<\infin>_ \frac x^" width="" height="" />
для всех \left(x\right) = \sum^<\infin>_ \frac x^" width="" height="" />
для всех

Читайте также: