Фазовая и групповая скорости кратко

Обновлено: 04.07.2024

Сигнал можно передать, используя импульс света. По теореме Фурье его можно разложить в ряд с частотами в интервале $\triangle \omega .$ Совокупность волн, которые различаются друг с другом, частотой в пределах малого интервала $\triangle \omega $ называют волновым пакетом (группой волн). Аналитически волновой пакет можно представить как:

где индекс $\omega $ у величин $A,\ k,\ \alpha $ показывает, что они относятся к разным частотам. В пределах пакета плоские волны усиливают друг друга, вне пакета происходит взаимное гашение волн. Для того чтобы сумму волн, которую описывает выражение (3), можно было считать пакетом, должно выполняться условие: $\triangle \omega \ll <\omega >_0.$

Групповая скорость

При отсутствии дисперсии все плоские волны в пакете распространяются с фазовой скоростью $v$. При таких условиях скорость распространения группы волн совпадает с фазовой скоростью, форма пакета постоянна. В веществе при наличии дисперсии пакет со временем ширина пакета увеличивается. При малой дисперсии, скорость перемещения центра пакета (точка, в которой максимальна величина $E$) называют групповой скоростью $(u).$ Групповая скорость характеризует импульс, и соответствует скорости распространения энергии поля этого импульса или скорость перемещения амплитуды.

При наличии дисперсии групповая и фазовая скорость различны:

Готовые работы на аналогичную тему

Если пакет представлен двумя составляющими, то групповую скорость можно найти как:

Групповая скорость пакета волн, который задан уравнением (3) может быть определена как:

если в разложении функции $k_<\omega >=k_0+<\left(\frac\right)>_0\left(\omega -<\omega >_0\right)+\dots \left(7\right)$ пренебречь членами высоких порядков. В выражении $<\left(\frac\right)>_0$- производная в точке $<\omega >_0$. В формуле (6) индекс $0$ опущен, так как не требуется. В таком приближении форма пакета волны постоянна во времени. Если в разложении (7) учесть следующие члены, то пакет волны будет расплываться.

Выражение для групповой скорости (6) можно записать в виде:

Связь групповой и фазовой скоростей (формула Рэлея)

Выражение для групповой скорости можно записать в виде:

Формула (9) называется формулой Рэлея. В том случае, если $\frac >0$ имеют дело с нормальной дисперсией, и $uv$. Выражение (9) можно представить как:

Выражение (10) показывает зависимость групповой скорости от характеристик вещества.

При введении понятия групповой скорости используют случай, когда дисперсия не велика. В противном случае пакет волн быстро деформируется и само понятие групповой скорости не имеет смысла. К примеру, около полосы поглощения среды, в области существенного изменения фазовой скорости в зависимости от частоты формула (9) может дать величину $u$ больше, чем скорость света в вакууме, или отрицательное значение. То есть в такой области формула Рэлея не применима.

Задание: Представьте групповую скорость в виде функции от показателя преломления и длины волны. Чему равна групповая скорость волн в воде, если $<\lambda >_1$=656,3 нм. Считайте, что при $t=20$ показатель преломления для этой длины воны $n_1=1,3311$, для $<\lambda >_2=643,8$ нм $n_=1,3314.$

Решение:

За основу решения задачи примем определение групповой скорости:

Зная, что круговая частота связана с длинной волны соотношением:

Волновой вектор можно записать как:

Подставим выражения (1.2) и (1.3) в (1.1), получим:

Подставим данные из условий задачи, проведем вычисления:

Ответ: $u\left(n,\lambda \right)=\frac\left(1+\frac<\lambda >\frac\right)=2,28\cdot ^8\frac.$

Задание: Найдите выражение групповой скорости ($u$), если фазовая скорость ($v$) представлена выражением: $v=a<\lambda >^q,$ где $a=const,\ q

Решение:

В качестве основы для решения задачи используем формулу Рэлея, определяющую групповую скорость вида:

Используя уравнение изменения фазовой скорости, заданное в условиях задачи найдем $\frac$, имеем:

Производная от расстояния по времени - это не что иное, как скорость перемещения фазы в пространстве, т.е. фазовая скорость . С учетом того, что , получаем

Таким образом, скорость, входящая в уравнение бегущей волны, – это фазовая скорость.

В общем случае фазовая скорость зависит от частоты волны, т.е. волны разных частот в одной и той же среде распространяются с разной скоростью. Это явление называется дисперсией.

Если волны, образующие волновой пакет, не обладают дисперсией, то картинка наложения волн, перемещаясь в пространстве, не изменяет своей формы.

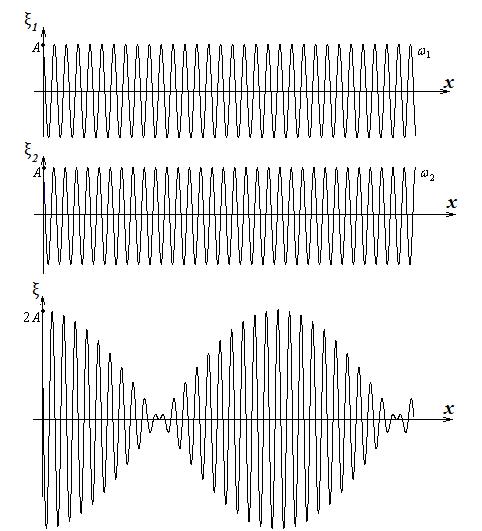
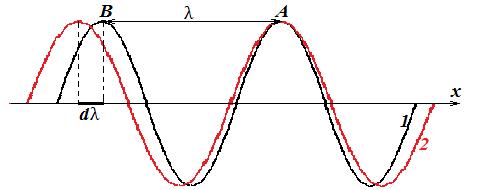
В рассмотренном примере вторая, более длинная волна, распространялась быстрее первой, более короткой волны ( ). Этот случай называют нормальной дисперсией. Групповая скорость в этом случае оказывается меньше фазовой.

Если более короткие волны в пакете будут бежать быстрее длинных ( ), то групповая скорость окажется больше фазовой. Это так называемая аномальная дисперсия.

В жизни практически всегда приходится сталкиваться не с бесконечной монохроматичной волной, а с волновым пакетом. Поэтому скорость волны, измеряемая на практике, это чаще всего групповая скорость.

В дальнейшем мы будем рассматривать в основном идеальный случай – бесконечную синусоидальную волну. Поэтому всюду, если это не оговорено особо, под скоростью волны будем понимать фазовую скорость.

Уточним введенное ранее понятие скорости волны.

Таким образом, скорость, входящая в уравнение бегущей волны, – это фазовая скорость.

Рассмотрено физическое содержание понятий фазовая скорость, групповая скорость и скорость переноса энерги и. Показано следующее.

Фазовая скорость есть скорость перемещения силовой характеристики поля (например, напряженности электрического поля).

Групповая скорость есть скорость перемещения интерференционной картины , образованной группой волн различных частот, распространяющихся в одном направлении. Групповая скорость не имеет никакого отношения к переносу энерги и этими волнами.

Скорость переноса энерги и монохроматической волной всегда совпадает по направлению с фазовой скоростью. В однородной безграничной среде она всегда равна по величине фазовой скорости. Показано, что при наличии граничных условий (например, в диэлектрическом или металлическом волноводах, в замедляющих структурах и т.д.) скорость переноса энерги и имеет простую связь с фазовой скоростью, но никогда не может превышать скорость света.

Введение

Движение электромагнитного поля, созданного системой зарядов или электромагнитной волной, связано с переносом электромагнитной энерги и и с перемещением вектора напряженности этого поля. Как известно, напряженность электрического поля числено равна силе, которая действует на единичный положительный точечный заряд, покоящийся в системе отсчета наблюдателя. Напряженность электрического поля перемещается с фазовой скоростью. Поэтому фазовую скорость мы можем назвать скоростью перемещения силовой характеристики этого поля.

Скорость переноса энерги и характеризует движение энерги и электрического или магнитного полей. Необходимость введения этого понятия возникла из-за широкого использования в радиоэлектронике линий передач энерги и и информации с дисперсионными свойствами. Это волноводы, замедляющие структуры, которые используются в электронных приборах СВЧ, в антеннах поверхностных волн, ускорителях и т.д.

В физике используется понятие групповой скорости. Групповая скорость это скорость перемещения волнового пакета, т.е. пакета, образованного группой волн. Поскольку электромагнитная энерги я сосредоточена в этом пакете, групповая скорость стала интерпретироваться как скорость переноса энерги и и начала играть ее роль. Однако применение понятия групповой скорости к монохроматической волне приводит к парадоксам. Мы начнем анализ с изложения доказательства, в котором вводится это понятие.

1. Групповая скорость

2. Парадокс

3. Вектор Пойнтинга

4. Проблемы определения скорости переноса энерги и

5. Скорость переноса энерги и ТЕ и ТМ волн

Левич В.Г. Курс теор етической физики. Т.1. – М.: Физматгиз, 1962.
Umov N.A. Beweg-Gleich. Energie in contin. Kopern, Zeitschriff d. Math. und Phys., v.XIX, Slomilch, 1874.
Кулигин В.А., Кулигина Г.А., Корнева М.В. Парадоксы релятиви стской механики и электродинамика / Воронеж. ун-т. – Воронеж, 1990. – 23 с. – Деп. в ВИНИТИ 24.07.90 №4180 – В90.
Вайнштейн Л.А. Электромагнитные волны. – М.: Сов. радио, 1957.

Об авторе:
Этот материал взят из источника в свободном доступе интернета. Вся грамматика источника сохранена.

Чем важнее ген, тем реже он мутирует
Изучение большого массива данных по мутагенезу у модельного растения Arabidopsis thaliana показало, что в разных участках генома мутации возникают с разной частотой. В результате получается, что частота возникновения новых мутаций связана обратной зависимостью с функциональной важностью данного участка генома и с силой действующего на него очищающего отбора. Иначе говоря, в наиболее важных участках новые мутации не только активнее вычищаются отбором, но и реже возникают.

Рассмотрим волновое движение в однородной и изотропной среде. Наиболее простым типом волны является плоская монохроматическая волна

которая представляет колебание с длиной волны распространяющееся в направлении волнового вектора с постоянной скоростью. Скорость, о которой идет речь, есть скорость перемещения плоскости равной фазы, или фазовая скорость

Согласно нашей гипотезе каждая частота соответствует вполне определенной энергии частицы

Естественно поэтому сопоставить волну (1) прямолинейному равномерному движению с энергией Е в направлении

Изучение классического приближения позволит нам связать с импульсом частицы. Для этого следует сопоставить частице волну конечной протяженности. Волна (1), конечно, не удовлетворяет этому требованию, но ему можно удовлетворить, если воспользоваться суперпозицией волн с близкими волновыми векторами. Это значит, что следует рассмотреть волновой пакет

Ради простоты рассмотрим вначале волновой пакет в одном измерении

тогда есть интеграл от произведения функции А, имеющей резкий максимум в области шириной окружающей точку и осциллирующей функции Если осцилляции функции в области достаточно многочисленны, то вклады различных частей области аннулируют друг друга, так что величина оказывается крайне малой. Наибольшие абсолютные значения получаются в том случае, когда фаза остается почти постоянной в области , т. е. (символ означает производную по когда Следует потребовать, чтобы имела не более одной осцилляции в области

волна практически локализована в области с размерами

Эта точка равномерно движется со скоростью

которая называется групповой скоростью волны Именно эта скорость а не фазовая скорость должна быть отождествлена со скоростью частицы в классическом приближении предельной локализации пакета:

Из условия и соотношения (2) находим соотношение де Бройля

Это рассуждение без труда обобщается на волновой пакет в трех измерениях: центр пакета равномерно перемещается со скоростью

причем групповая скорость должна быть отождествлена со скоростью частицы

Последнее сотношение вместе с соотношением (2) позволяет найти связь между динамическими переменными частицы и величинами, характеризующими ассоциированную ей волну:

Эти соотношения идентичны соотношениям (1.4), полученным для случая фотона.

В заключение рассмотрим полученные результаты с точки зрения принципа относительности.

В нерелятивистском приближении энергия Е определяется только с точностью до некоторой постоянной; изменить начало отсчета энергии значит добавить к частоте некоторую постоянную частоту (уравнение (2)), т. е. умножить функцию на фазовый фактор Это не меняет предшествующих результатов, касающихся движения волнового пакета, и соотношений (5), которые из них вытекают.

Однако полученные результаты ни в коей мере не зависят от нерелятивистского приближения. Принцип относительности позволяет определить точную энергию и соответствующую ей частоту со. Энергия Е и импульс являются компонентами одного -вектора (принимаем ). То же самое можно сказать относительно частоты и волнового вектора Соотношения (5) удовлетворяют принципу относительности: они означают, что -векторы пропорциональны друг другу.

3. Уравнение плоской бегущей волны в комплексном виде.

4. Разность фаз колебаний.

6. Фазовая и скорость.

7. Групповая скорость.

8. Связь фазовой и групповой скорости.

9. Нахождение групповой скорости методом Эренфеста.

10. Уравнение сферической волны.

11. Вывод уравнения стоячей волны.

12. Координаты узлов и пучностей.

13. Энергия волн.

Длина волны и волновое число

Длиной волны – называют расстояние между ближайшими точками, колеблющимися в одинаковой фазе.

Формулы длины волны легко получить из аналогии по формуле пути:

Если период равен , (3)

Если из (2) выразить период и приравнять его к (3), получим:

Физический смысл отношения заключается в том, что оно показывает сколько длин волн умещается в единицах длины. Отношение обозначается и называется волновым числом, т.е.

Вывод уравнения плоской бегущей волны

Бегущие волны – волны, которые переносят в пространстве энергию.

Плоские волны – волны, волновые поверхности которых – есть совокупность параллельных плоскостей, перпендикулярных направлению распространения волны.

Лучи в этом случае – параллельные прямые, совпадающие с направлением скорости распространения волны.

Пусть плоская бегущая волна распространяется вдоль оси X, т.е. вдоль одного направления из точки А в точку В как показано на рисунке:

Пусть источник колебаний в начальный момент времени находится в точке О.

Запишем уравнение колебания:

Рассмотрим распространение волны от точки М до точки В. Из рисунка видно, что время , затраченное на этот путь равно , где - это время, за которое волна распространилась от источника колебаний до точки М.

Перейдем от уравнения колебаний к уравнению плоской бегущей волны:

Т.к. за время волна распространилась на расстояние , тогда

Будем считать начальную фазу .

Тогда согласно уравнению (6), получаем: (14)

Если в уравнении (14) , а , то получим четвертый вид уравнения плоской бегущей волны (при ):

- первый вид уравненияплоской бегущей волны

- второй вид уравненияплоской бегущей волны

- третий вид уравненияплоской бегущей волны

- четвертый вид уравненияплоской бегущей волны

- смещение точек среды с координатой x в момент времени t.

Уравнение плоской бегущей волны в комплексном виде.

Уравнение плоской бегущей волны можно представить в комплексном виде, используя формулу Эйлера:

Т.к. физический смысл имеет только реальная часть, получаем:

Получаем уравнение плоской бегущей волны комплексном виде:

- уравнения плоскойбегущей волны в комплексном виде

Разность фаз колебаний

Фаза рассчитывается из определения углового перемещения:

Виды волн

Основное свойство всех волн – перенос частицами среды энергии без переноса вещества.

Различают продольные и поперечные волны.

Волны, в которых частицы среды колеблются вдоль их распространения, называются продольными.

Волны, в которых частицы среды колеблются в плоскостях, перпендикулярных к направлению распространения волны, называются поперечными.

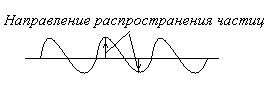
Продольные волны распространяются в жидкостях и газах

В твердой среде возникают как продольные, так и поперечные

Фазовая скорость

Пусть в волновом процессе фаза = const, т.е.

После дифференцирования, получим:

Вывод: скорость распространения волны есть скорость перемещения фазы волны, поэтому ее называют фазовой скоростью и обозначают: :

Дисперсией называется зависимость фазовой скорости в среде от частоты распространение волн (дисперсия всегда связана с поглощением энергии средой)

Групповая скорость

Рассмотрим простейшую группу волн, которая получается при наложении двух плоских волн с одинаковыми амплитудами и близкими частотами и близкими волновыми числами :

Это волна отличается от гармонической тем, что ее амплитуда есть медленно изменяющаяся функция координаты от времени, т.е. является негармонической.

- амплитуда группы волн

Групповая скорость– скорость распространения группы волн,

Групповая скорость– скорость максимума огибающей группы волн или скорость движения центра волнового пакета.

- групповая скорость

Связь групповой и фазовой скорости.

Групповая скорость определяется выражением:

Определим отдельно выражения для и :

Из выражения выразим угловую скорость: (33)

Продифференцируем это выражение по k: (34)

Выражения продифференцируем по :

Подставим выражения (34) и (35) в выражение для групповой скорости (32), получим:

- связь фазовой и групповой скорости

Из (38) следует, что может быть как больше, так и меньше фазовой в зависимости от знака .

Если в среде не наблюдается дисперсия волн, то , тогда фазовая и групповая скорости совпадают .

Понятие групповой скорости очень значимо, т.к. именно она фигурирует при измерении дальности радиолокации, в управлении космическими объектами.

Но , а для ограничений нет.

9. Нахождение групповой скорости методом Эренфеста

Зависимость групповой скорости от длины волны позволяет определить значение групповой скорости.

Для этого нужно провести касательную к точке с координатами и . Можно найти отрезок, отсекаемый касательной на оси ординат, равный значению групповой скорости.

Читайте также: