Евклидова геометрия и неевклидова геометрия кратко

Обновлено: 04.07.2024

Статья написана в легком развлекательном стиле. И попытки разобраться в каких-то математических определениях могут вызвать некоторый интерес.

Правила в природе есть, обязательно и непреложно, хоть у песчинки, хоть у капли воды, а человек только правила обнаруживает и их осмысливает. Причем, поиски решений многовариантны, как и сама Природа и пути развития. Да Вы и сам в конце статьи это признаете.
Поэтому, два плюс три будет равно пяти - это следствие действий законов природы, по которым функционируют мозг, органы чувств и симпатическая система человека. Опять же, если не понимать смысла почему умножение выполняется в первую очередь, то зачем вообще браться за эту тему? Еще и интегрирование гении придумали для простоты применения в хозяйственной деятельности.
Вот чего в Природе точно нет, так это прямых линий.

Странно, чем четырехмерное пространство имеет бОльшую ограниченность, чем трехмерное?

Опять же, чтобы, как вы выразились, перейти к реальному положению вещей в природе до построения точки в плоской математической модели, мы сначала определяем пространство, которое хотим изучать. Точка - это уже объект. И эта точка как объект описывается как минимум одной функцией. Если это сложный объект, то точка имеет очень много функций. Но математически она может лежать как в двухмерном изображении, так и в любом многомерном изображении. Смотря какое пространство, какой процесс, среду или объект вы рассматриваете. Проведенная через точку прямая - это тоже функция. Как "считает земная логика" - это исключительно субъективное восприятие. Главное, что для человека существует по его интеллектуальной природе определенные взаимосвязи в познании от простого к сложному. Интеллект делится условно по качеству: 1. кристаллизующийся из накопленного опыта и навыков, отвечает за извлечение знаний и применение их в привычных условиях от частного - к общему, где не требуется включения подвижного интеллекта, основывается на вербальных процессах; 2. подвижный отвечает за построение сложных образных конструктов и раскрытие причинно-следственных связей, дедуктивное мышление от общего - к частному, оперирование с массивами информации.

/Опять же, если не понимать смысла почему умножение выполняется в первую очередь, то зачем вообще браться за эту тему?/
Опять же, если предъявляете непонимание по какому-то вопросу, и не приводите оснований, то зачем вообще спрашивать?
/Странно, чем четырехмерное пространство имеет бОльшую ограниченность, чем трехмерное?/
Это где Вы нашли у меня такое?

Роман, Вы же пишете: ". бОльшая ограниченность всегда получается зависимой от меньшей. Т.е., сначала идёт более многомерное пространство, а затем менее многомерное. " Поэтому, я интересуюсь аргументами из вашего залючения: "чем четырехмерное пространство имеет бОльшую ограниченность, чем трехмерное?

Большая ограниченность зависима от меньшей – значит то, что больше ограничено, зависимо от того, что ограничено меньше. 3хмерка больше ограничена, значит, она зависима от того, что ограничено меньше – 4хмерки. Не наоборот.

Портал Проза.ру предоставляет авторам возможность свободной публикации своих литературных произведений в сети Интернет на основании пользовательского договора. Все авторские права на произведения принадлежат авторам и охраняются законом. Перепечатка произведений возможна только с согласия его автора, к которому вы можете обратиться на его авторской странице. Ответственность за тексты произведений авторы несут самостоятельно на основании правил публикации и законодательства Российской Федерации. Данные пользователей обрабатываются на основании Политики обработки персональных данных. Вы также можете посмотреть более подробную информацию о портале и связаться с администрацией.

На этот вопрос можно ответить несколькими разными способами.

1) От всякой точки до всякой точки можно провести прямую.

2) Ограниченную прямую можно непрерывно продолжать по прямой.

3) Из всякого центра всяким радиусом может быть описан круг.

4) Все прямые углы равны между собой.

5) Если прямая, пересекающая две прямые, образует внутренние односторонние углы, меньшие двух прямых, то, продолженные неограниченно, эти две прямые встретятся с той стороны, где углы меньше двух прямых.

Второй способ - геометрический. Евклидова геометрия естественным образом реализуется на плоскости. Если же в качестве поверхности взять не плоскость, а другую поверхность, то на ней мы получим неевклидову геометрию. К сожалению, в трёхмерном пространстве нельзя представить такую двумерную поверхность, которой бы соответствовала бы плоскость Лобачевского. Но есть поверхности, на которых реализуется геометрия Лобачевского. Такая поверхность должна иметь постоянную отрицательную кривизну. Простейший пример - псевдосфера. В качестве прямых на поверхности выступают геодезические линии. Углы между ними определяются как углы между соответствующими касательными проведёнными к соответствующим геодезическим, например. И т.д. Можно рассмотреть геометрию на сфере: сумма углов любого треугольника будет больше pi (в то время как сумма углов любого треугольника в плоскости лобачевского строго меньше pi). Геометрией на сфере пользуются авиакомпании для прокладывания кратчайших маршрутов, например=)

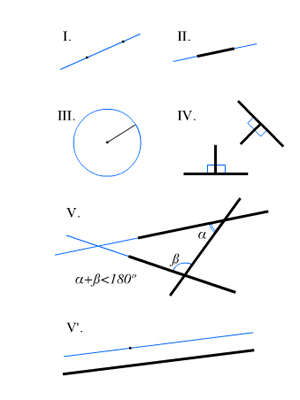
От всякой точки до всякой точки можно провести прямую.
Ограниченную прямую можно непрерывно продолжать по прямой.
Из всякого центра всяким раствором может быть описан круг.
Все прямые углы равны между собой.
Если прямая, пересекающая две прямые, образует внутренние односторонние углы, меньшие двух прямых, то, продолженные неограниченно, эти две прямые встретятся с той стороны, где углы меньше двух прямых.

Тщательное изучение аксиоматики Евклида во второй половине XIX века показало её неполноту. В 1899 году Д. Гилберт предложил первую строгую аксиоматику евклидовой геометрии. Впоследствии еще не раз ученые предпринимали попытки усовершенствовать аксиоматику евклидовой геометрии. Кроме аксиоматики Гилберта, известными считаются: аксиоматики Тарского и аксиоматики Биргофа, которая состоит всего лишь из 4 аксиом.

В современной трактовке система аксиом Евклида может быть разделена на пять групп:

Аксиомы сочетания. Во-первых, через каждые две точки можно провести прямую и притом только одну. Во-вторых, на каждой прямой лежат по крайней мере две точки. При этом существуют хотя бы три точки, которые не лежат на одной прямой. В-третьих, через каждые три точки, не лежащие на одной прямой, можно провести плоскость и притом только одну. В-четвертых, на каждой плоскости есть по крайней мере три точки, а также существуют хотя бы четыре точки, не лежащие в одной плоскости. В-пятых, если две точки данной прямой лежат на данной плоскости, значит и сама прямая лежит на этой плоскости. В-шестых, если две плоскости имеют общую точку, то, следовательно они имеют и общую прямую.
Аксиомы порядка. Во-первых, если точка В лежит между А и С, то все три лежат на одной прямой. Во-вторых, для каждых точек А, В существует такая точка С, что В лежит между А и С. В-третьих, из трёх точек прямой только одна лежит между двумя другими. В-четвертых, если прямая пересекает одну сторону треугольника, значит она пересекает при этом и другую его сторону или проходит через вершину (отрезок AB определяется как множество точек, лежащих между А и В; аналогично определяются стороны треугольника).
Аксиомы движения. Во-первых, движение ставит в соответствие точкам точки, прямым прямые, плоскостям плоскости, сохраняя принадлежность точек прямым и плоскостям. Во-вторых, два последовательных движения вновь дают движение, и для всякого движения есть обратное. В-третьих, если даны точки А, A’ и полуплоскости A, A‘, ограниченные продолженными полупрямыми а, а’, которые исходят из точек А, A’, то существует единственное движение, переводящее А, а, A в A’, a’, A’ (полупрямая и полуплоскость легко определяются на основе понятий сочетания и порядка).
Аксиомы непрерывности. Во-первых, как гласит аксиома Архимеда, всякий отрезок можно перекрыть любым отрезком, откладывая на первом его достаточное количество раз (откладывание отрезка осуществляется движением). Во-вторых, согласно аксиоме Кантора: если дана последовательность отрезков, вложенных один в другой, то все они имеют хотя бы одну общую точку.
Аксиома параллельности Евклида: через точку А вне прямой а в плоскости, проходящей через А и а, можно провести лишь одну прямую, не пересекающую а.

Евклидова геометрия стала результатом систематизации и обобщения наглядных представлений человека об окружающем мире. Углубленное проникновение в суть геометрии привело к более абстрактному пониманию науки. Более поздние достижения и открытие показали, что наши представления о пространстве являются априорными, то есть чисто умозрительные. Таким образом было поставлено под сомнение существование единственной геометрии. бурное развитие физики и астрономии, доказало, что евклидова геометрия описывает структуру окружающего пространства, но вовсе не способна описать свойства пространства, связанные с перемещениями тел со скоростями, близкими к световой. Русский математик Н. И. Лобачевский разработал новую неевклидову геометрию, которая приблизилась к реальному описанию физического пространства.

НЕЕВКЛИДОВА ГЕОМЕТРИЯ, геометрия, сходная с геометрией Евклида в том, что в ней определено движение фигур, но отличающаяся от евклидовой геометрии тем, что один из пяти ее постулатов (второй или пятый) заменен его отрицанием. Отрицание одного из евклидовых постулатов (1825) явилось значительным событием в истории мысли, ибо послужило первым шагом на пути к теории относительности.

Из этих пересмотренных постулатов следовало, что сумма углов треугольника, равная 180 ° в евклидовой геометрии, больше 180 ° в эллиптической геометрии и меньше 180 ° в гиперболической геометрии.

История.

В 1854 Б.Риман (1826–1866) заметил, что из неограниченности пространства еще не следует его бесконечная протяженность. Смысл этого утверждения станет яснее, если представить, что в неограниченной, но конечной вселенной астроном в принципе мог бы увидеть в телескоп, обладающий достаточно высокой разрешающей способностью, свой собственный затылок (если отвлечься от небольшой детали, связанной с тем, что свет, отраженный от затылка, достиг бы глаза астронома через тысячи миллионов лет). В своем доказательстве того, что внешний угол при любой вершине треугольника больше внутреннего угла при любой из двух остальных вершин, Евклид неявно использовал бесконечную длину прямой. Из этой теоремы тотчас же следует теорема о том, что сумма любых двух углов треугольника меньше суммы двух прямых углов. Если отказаться от бесконечной длины прямой, то гипотеза Саккери о тупом угле становиться верной и из нее следует, что сумма углов треугольника больше суммы двух прямых. Такое положение дел было давно известно в сферической тригонометрии, где стороны треугольника являются дугами больших кругов. Риман внес эпохальный вклад, распространив представление о конечном, но неограниченном пространстве с двух на три и большее число измерений.

Эллиптическая плоскость.

Геометрия порядка.

Абсолютная геометрия.

Гиперболическая плоскость.

П(x) = 2arctg e –x .

Евклидовы модели неевклидовых геометрий.

А.Пуанкаре (1854–1912) открыл представление гиперболического пространства с помощью конформной модели, в которой геометрическое место концов имеет вид плоскости W в евклидовом пространстве, а сферам с центрами в W соответствуют плоскости гиперболического пространства. Заменив сферы полусферами, Пуанкаре получил возможность представить все гиперболическое пространство с помощью половины евклидова пространства, а именно всеми точками, лежащими по одну сторону от W . Один пучок концентрических орисфер представлен плоскостями, параллельными W ; можно доказать, что евклидовы расстояния в такой плоскости пропорциональны соответствующим геодезическим на орисфере, что полностью согласуется с наблюдением Вахтера.

Рассматривая сечение трехмерной модели Пуанкаре плоскостью, перпендикулярной W , мы получим модель аналогичную модели Пуанкаре для гиперболической плоскости. В этой модели геометрическое место концов имеет вид евклидовой прямой. В другой модели геометрическое место концов имеет вид окружности w , а прямые на гиперболической плоскости – дуг окружностей, ортогональных w . Две параллельные дуге r, проходящие через точку B, – просто дуги, проходящие через точку B и касающиеся дуги r в ее концах, как на рис. 5.

Читайте также: