Элементы фурье оптики кратко

Обновлено: 02.07.2024

Преобразование Фурье в оптике обладает физической реализацией. Так, каждая оптическая система при дифракции в когерентных волнах создает соответствие между освещенным объектом и его изображением на плоскости. Эта плоскость определяется законами геометрической оптики. Изображение -- двумерный фурье образ, определяют законы дифракции. Формирование изображений и преобразования Фурье -- проявления явления дифракции.

В задачах оптики интерес вызывает пространственная структура светового поля, которая задается в плоскости в виде функции от координат. Эта функция -- комплексная амплитуда поля.

Спектральное разложение на основании преобразований Фурье дает возможность представить любое поле света как суперпозицию плоских монохроматических волн. Вследствие линейности волнового уравнения каждая волна распространяется независимо от других. Такая ситуация позволяет привести анализ преобразования сложного поля к преобразованию простой волны. Суммарное поле находят как суперпозицию волн, прошедших через дифракционную систему.

Фраунгоферова дифракция как пространственное преобразование Фурье

Допустим, что световая волна плоская, но имеет в поперечном сечении участки с полем равным нулю. Она распространяется и достигает экрана. Пусть поле, которое было бы сзади экрана, если бы строго соблюдались законы геометрической оптики, обозначается $E_0$. Часть плоскости поперечного сечения волны на которой $E_0\ne 0$ будет обозначена $S$. Так как любая такая плоскость будет волновой поверхностью плоской волны, то $E_0=const$ вдоль всей площади $S$. Следует отметить, что волна с ограниченной площадью поперечного сечения не может быть абсолютно плоской. В ее пространственное разложение Фурье войдут компоненты с волновыми векторами разных направлений (именно это является источником дифракции).

Сделаем разложение поля $E_0$ в двумерный интеграл Фурье по координатам y,z в плоскости поперечного сечения волны. Компоненты Фурье имеют вид:

где $q$ -- постоянный вектор в плоскости $YZ$. Фактически интегрирование в (1) ведется по части $S$ плоскости $YZ$, где $E_0\ne 0.$ В том случае, если $\overrightarrow-\ $волновой вектор падающей волны, то полевой компоненте $E_qe^$ отвечает вектор, определяемый как:

Готовые работы на аналогичную тему

Получаем, что вектор $\overrightarrow$ определяет изменение волнового вектора при дифракции. Так как абсолютные значения векторов $k'=k=\frac<\omega >$, малые углы дифракции $_y,\ _z$ в плоскостях $XY$ и $XZ$ определены как:

В случае малых отклонений от геометрической оптики (малые углы отклонения от первоначального направления лучей) составляющие разложения поля $E_0$ можно считать такими же, как компоненты истинного света подвергшегося дифракции, так что формула (1) определяет распределение по направлениям интенсивности дифрагированного света на больших расстояниях от экрана.

Линза как элемент, который реализует преобразование Фурье

Тонкая линза выполняет такое преобразование фазы плоской волны, что она преобразуется в сферическую сходящуюся или расходящуюся волну. При этом распределение амплитуд в фокальной плоскости линзы есть образ Фурье распределения амплитуд на входе в линзу. Точность при этом достаточно велика (масштабные и фазовые множители). Этот факт определен тем, что дифракционная картина в фокальной плоскости линзы описывается формулой:

$n$ -- показатель преломления вещества линзы, $_0$ -- максимальная толщина линзы, $\Psi'\left(x',y'\right)-\ $амплитуда волны на входе в линзу, $f$ -- фокусное расстояние линзы.

Задание: Поясните, что такое коэффициент пропускания линзы, как он связан с фокусным расстоянием линзы и коэффициентом преломления вещества, из которого линза изготовлена.

Решение:

Запишем выражение для фазы волны, если $n$ -- показатель преломления вещества линзы, $_0$ -- максимальная толщина линзы, в таком случае полная фаза изменения волны при прохождении пути от левой одной плоскости линзы до другой равно:

\[\varphi \left(x,y\right)=kn\triangle \left(x,y\right)+k\left[\triangle_0-\triangle \left(x,y\right)\right]=k\triangle_0+k(n-1)\triangle (x,y)\left(1.1\right),\]

$\triangle \left(x,y\right)$- функция толщины линзы.

Величина $\tau \left(x,y\right)$ определяемая как:

называется коэффициентом пропускания линзы. Используя (1.1) получим, что:

Для линзы коэффициент пропускания исключительно фазовый. Для фокусного расстояния линзы имеется соотношение вида:

где $R_1$, $R_2$ -- радиусы кривизны линзы. При расчете функции толщины линзы считаем, что радиус кривизны выпуклой поверхности по ходу луча считают положительным, радиус кривизны вогнутой поверхности -- отрицательным. Для $\triangle \left(x,y\right)$ можно записать:

Тогда выражение для $\varphi (x,y)$ получит вид:

В таком случае выражение для $\tau \left(x,y\right)\ $примет вид:

Задание: На основании результатов, полученных в предыдущем примере, поясните какие величины в выражении для коэффициента пропускания линзы отвечают за преобразование плоской волны в сферическую. При каких условиях волна является расходящейся, при каких сходится?

Решение:

Рассмотрим выражение для коэффициента пропускания линзы, которое представлено как:

Множитель $e^_0>$ в выражении (2.1) не ведет к искажению формы фронта плоской волны, когда свет проходит через линзу. Множитель $e^>$ переводит плоскую волну в сферическую. Эта волна может быть сходящейся или расходящейся. Это обстоятельство зависит от знака экспоненты. Если $f>0$, вторая экспонента в выражении (2.1) отрицательна, то периферические части волны терпят меньшую задержку фазы, чем центр волны в ходе прохождения линзы. Как результат - сходящаяся сферическая волна.

-раздел оптики, в к-ром преобразование световых полей оптич. системами исследуется с помощью фурье-анализа (спектрального разложения) и теории линейной фильтрации. Начало использования в оптике идей спектрального разложения связано с именами Дж. Рэлея (J. Rayleigh) и Э. Аббе (Е. Abbe). Первые работы, к-рые легли в основу совр. Ф.-о., принадлежат Мандельштаму [1], Горелику [2], Рытову [3]. В последней проводится аналогия между задачами радиоэлектроники и теории связи, с одной стороны (в к-рых речь идёт о преобразовании сигналов-ф-ций времени-изменяющихся токов, напряжений и т. д. и о системах радиоэлектроники, регистрирующих эти преобразования), и задачами оптики- с другой, в к-рых рассматривается преобразование световых полей-ф-ций координат-оптич. системами.

Общность методов исследования систем, служащих для преобразования сигналов - ф-ций времени (временных фильтров), и оптич. систем, служащих для преобразования световых полей - ф-ций координат (пространств. фильтров), обусловлена общностью закономерностей, управляющих процессами в системах радиоэлектроники и оптики, общностью, заложенной в универсальности максвеллов-ских ур-ний электродинамики. И тем и другим системам присущи (в достаточно широкой области применений) такие фундаментальные свойства, как линейность и инвариантность. Это позволяет удобно и просто описывать их поведение единым образом, используя универсальный аппарат теории линейной фильтрации и преобразования Фурье.

Основные понятия и соотношения Ф.-о. В радиоэлектронике систему, преобразующую сигналы, принято изображать в виде схемы (рис. 1, а), где внеш. воздействие f(t) есть входной сигнал фильтра, а результат этого воздействия g(t) - выходной сигнал (или отклик) фильтра. Примером временного фильтра является колебат. контур (рис. 1, б), в к-ром внеш. эдс - входной сигнал, а возникающие изменения напряжения на обкладках конденсатора- отклик фильтра. Тот факт, что ф-ция g(t )является откликом на входное воздействие f(t), записывают в виде операторного равенства

Волновые (в частности, оптические) явления характеризуются как временной зависимостью, так и пространственной, т. е. зависимостью от координат. В Ф.-о. интерес представляет именно пространств. структура волны, к-рая описывается (в случае гармонич. волн фиксированной частоты w) комплексной амплитудой волны f(x, у, z), являющейся решением ур-ния Гельмгольца:

(k = w/c- волновое число). [Комплексная амплитуда, определяющая распределение амплитуд и фаз колебаний является входным и выходным сигналом когерентной оптич. системы. При некогерентном освещении говорят о картинах интенсивности (а не об амплитудах) во входной и выходной плоскостях.]

В процессе распространения волны через оптич. систему её пространств. структура изменяется. Такая система рассматривается как пространственный фильтр, преобразующий входной сигнал (комплексную амплитуду волны во входной плоскости оптич. системы) в выходной сигнал (комплексную амплитуду волны в выходной плоскости оптич. системы). На рис. 2 представлена схема пространств. фильтра ( а )и пример простейшей оптич. системы ( б), где f(x, у) - комплексная амплитуда волны во входной плоскости П 0 , g(x, у) - комплексная амплитуда в выходной плоскости П 1 . Соответствующее операторное равенство имеет вид

В радиоэлектронике свойства линейного фильтра характеризуются импульсным откликом h(t, t) - откликом фильтра на входной d-импульс:

Здесь h(t,t) - ф-ция времени t, параметр t указывает, что речь идёт об отклике на d-импульс, возникающий на входе в момент времени t = t.

Аналогом d-импульса, возбуждающего колебания в линейном фильтре, в задачах пространств. фильтрации является точечный источник света d(x -x, у -h), расположенный в точке x = x, у =hвходной плоскости ху. При этом в выходной плоскости возникает нек-рое световое поле с комплексной амплитудой h(x, у;x, h), являющейся ф-цией координат х, у ввыходной плоскости. Поле h(x, у;x, h) наз. ф у н к ц и е й р а с с е я н и я т о ч к и и является аналогом импульсного отклика линейного временного фильтра.

Т. о., выражение (11) есть представление произвольной волны, заданной в нек-рой плоскости z = const, в виде суперпозиции плоских волн, как бегущих, так и неоднородных.

Плоская волна ехр[i(ux + uy)] в задачах пространств. фильтрации является аналогом гармонич. колебания ехр iwt. Поэтому пару чисел и,uназ. пространственными частотами.

Пространственная модуляция. В радиоэлектронике модуляция сигнала записывается как операция перемножения модулируемого колебания f(t) и модулирующего сигнала m(t), в результате к-рой на выходе модулятора имеем модулированный сигнал g(t)=f(t)m(t). Различают два вида модуляции: амплитудную, когда m(t) - действительная положит. ф-ция a(t), и фазовую: m(t) = ехр ij(t). Если несущее (модулируемое) колебание - гармонич. ф-ция f(t) = = ехр iwt, то в первом случае на выходе имеем амплитуд-но-модулированное колебание g(t) = a(t)exp iwt, а во втором- колебание, модулированное по фазе g(t) = = ехрi[wt+j(t)]>. Операцию модуляции изображают символически с помощью блок-схемы (рис. 4, а).

Пространств. модуляция осуществляется в оптике с помощью тонких пластинок-транспарантов,- обладающих в разных точках разл. поглощательной способностью и (или) показателем преломления. При освещении пластинки плоской волной expi(ux +uy )это приводит к тому, что амплитуда волны на выходе из пластинки оказывается различной в разных точках (в соответствии с изменением поглощат. способности), т. е. имеем амплитудную модуляцию волны:

Если пластинка имеет различный в разных точках показатель преломления п(х, 1 и Л 2 с общей фокальной плоскостью Ф; входной плоскостью П 0 (где размещается предмет) служит передняя фокальная плоскость линзы Л 1 , а выходной плоскостью, где возникает изображение,- задняя фокальная плоскость линзы Л 2 - плоскость П t .

Формирование изображения в оптич. системе, согласно теории Аббе,- двухэтапный процесс. Первый этап (первая "дифракция")-это распространение света от входной плоскости до плоскости Ф, где формируется пространств. спектр предметной волны. На этом этапе линза Л 1 осуществляет первое пространств. фурье-преобразова-ние. Второй этап (вторая дифракция) - распространение света от плоскости Ф (к-рая наз. фурье-плоскостью оптич. системы) до плоскости изображения. На этом этапе линза Л 2 осуществляет ещё одно преобразование Фурье. В результате двух последоват. преобразований Фурье возникает перевёрнутое изображение-поле с комплексной амплитудой g(x,y)=f(-x, -у), тождественное с точностью до инверсии предметному полю f (х, у).

В действительности же оптич. система вносит искажения. Принципиальными являются дифракц. искажения, обусловленные конечностью размеров линз. Влияние конечных размеров линз моделируется диафрагмой, расположенной в фурье-плоскости оптич. системы (рис. 6) (диаметр диа-

фрагмы D равен диаметру меньшего из объективов). В формировании изображения в такой модели принимают участие лишь те плоские волны, к-рые фокусируются линзой Л 1 внутрь диафрагмы, т. е. волны с пространств. частотами

Эти волны приходят к плоскости изображения П 2 без искажений по амплитуде и фазе. Все прочие волны, задерживаясь диафрагмой, не достигают плоскости изображения, т. е. оптич. система имеет частотную характеристику:

(т. н. дифракционно-ограниченная система). Ф-ция рассеяния [обратное фурье-преобразование ф-ции (15)] имеет вид

Принцип корреляционной фильтрации. Т. к. плоские волны разных пространств. частот, фокусируясь линзой Л 1 в разные точки фурье-плоскости, пространственно разделяются, то можно избирательно воздействовать на разл. пространств. гармоники. Если маленькую пластинку-транспарант, вносящую определ. поглощение и (или) определ. фазовую задержку, поместить в точку ( х, у )фурье-плоскости, то эта пластинка изменит амплитуду и (или) фазу только той плоской волны, к-рая в эту точку фокусируется (т. е. волны с частотой u= kx/f,u=ky/f). При этом все др. волны достигают плоскость изображения без искажений по амплитуде и фазе. Помещая в фурье-плоскость разл. маски-транспаранты, можно непосредственно влиять на пространств. спектр изображения.

Маска с ф-цией пропускания т(х, k (w) = F k (w)|H(w)| 2 , где H(w)-частотная характеристика фильтра. Аналогичное равенство справедливо для решения задачи фильтрации спекл-полей в оптич. (пространств.) фильтрах:

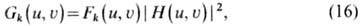
где G k (u, u)и F k (u,u) - пространств. спектры мощности (фурье-образы автокорреляц. ф-ций) спекл-полей во входной и выходной плоскостях оптич. системы.

В соответствии с (16) управление характеристиками системы для фильтрации спекл-полей осуществляется с помощью амплитудных транспарантов.

Некогерентные оптические системы. В некогерентных системах входным и выходным сигналами являются интенсивности света I вx ( х, у )и I вых ( х, у )во входной и выходной плоскостях. Связь между ними определяется равенством

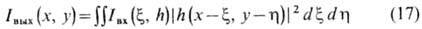
(при выполнении условия изопланатичности).

Из (17) следует связь между нормированными спектрами (фурье-преобразованиями) ф-ций I вх ( х, у )и I вых ( х, у):

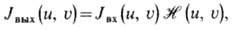
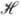
где J вх (u, u)и J вых (u, u)-фурье-образы ф-ций J вх (x, у )и I вых (x, y); (u, u)- п е р е д а т о ч н а я ф у н к ц и я оптич. системы, определяющая свойства некогерентной оптич. системы.

Связь между когерентной частотной характеристикой H (и,u)и передаточной ф-цией оптич. системы ( и, u)для одномерного случая имеет вид

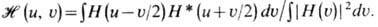
Возможности использования идей и методов Ф.-о. существенно расширяются с применением динамически управляемых ячеек и транспарантов, располагаемых в фурье-плоскости оптич. системы: жидких кристаллов, ультразвуковых ячеек, эл.-оптич. ячеек Керра и т. д.

Лит.: Горелик Г. С., Колебания и волны, 2 изд., М., 1959; Рытов С. М., О методе фазового контраста в микроскопии, "УФН", 1950, т. 41, в. 4, с. 425; О'Нейл Э., Введение в статистическую оптику, пер. с англ., М., 1966; Строук Дж., Введение в когерентную оптику и голографию, пер. с англ., М., 1967; Гудмен Дж., Введение в фурье-оптику, пер. с англ., М., 1970; его же, Статистическая оптика, пер. с англ., М., 1988; Сороко Л. М., Основы голографии и когерентной оптики, М., 1971; Папулис А., Теория систем и преобразований в оптике, пер. с англ., М., 1971; Мандельштам Л. И., Лекции по оптике, теории относительности и квантовой механике, М., 1972; Зверев В. А., Радиооптика, М., 1975; Юу Ф., Введение в теорию дифракции, обработку информации и голографию, пер. с англ., М., 1979. Г. Р. Лакшин.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия . Главный редактор А. М. Прохоров . 1988 .

Оптика Фурье (названная в честь Джозефа Фурье ), является полем волновой оптики на основе концепции преобразования Фурье .

Резюме

Основной инструмент: дифракция Фраунгофера.

Волновая оптика в основном использует принцип Гюйгенса-Френеля для достижения таких результатов, как щели Юнга или пятно Эйри . Эти расчеты относительно сложны, и для их упрощения можно поместить себя в рамки определенных приближений. Например, дифракция Фраунгофера предполагает, что дифракционная картина наблюдается на очень большом расстоянии от дифрагирующего объекта.

Формула фраунгофера

Эти приближения позволяют появиться преобразованию Фурье в формуле дифракции: где:
E ( Икс , y , z ) ∝ F [ В я т ] ( ж Икс , ж y ) > _ _ t \ right]> \ left (f_ , f_ \ right)>

Дифракционная диаграмма, полученная в условиях Фраунгофера для квадратной апертуры. Мы узнаем двумерный кардинальный синус.

Главное следствие

Приведенная выше формула позволяет получить следующий результат: плоская волна при нормальном падении на объект сформирует до бесконечности свое преобразование Фурье. Точнее, он образует преобразование Фурье коэффициента пропускания объекта.

Действительно, для плоской волны при нормальном падении амплитуда однородна в плоскости падения, что позволяет исключить ее из преобразования Фурье. Это листья: . В я _ > E ( Икс , y , z ) ∝ F [ т ] ( ж Икс , ж y ) > _ \ left (f_ , f_ \ right)>

Одно из основных последствий можно увидеть на примере камеры. Диафрагмы оптической системы действует как дифрагирующую поверхность , и изображение точки представляет собой преобразование Фурье этого элемента.

Говорят, что такая оптическая система ограничена дифракцией и действует как фильтр по отношению к пространственным частотам фотографируемой сцены. Таким образом, оптика Фурье позволяет понять, что при любом качестве оптики невозможно сфотографировать слишком высокие пространственные частоты.

Практическая реализация

Дифракция Фраунгофера действительна только на бесконечности , но вместо того, чтобы помещать ее на бесконечность , мы предпочитаем использовать собирающую линзу . В самом деле, можно показать, что дифракция фраунгофера действительна также в фокальной плоскости изображения линзы. Это позволяет вернуть преобразование Фурье исследуемого объекта на конечное расстояние.

Таким образом, мы можем наблюдать преобразование Фурье различных объектов следующим способом (см. Диаграмму): мы помещаем объект на путь луча света и добавляем собирающую линзу после объекта. Поместив экран в фокальную плоскость этой линзы, наблюдаемая фигура будет преобразованием Фурье объекта. Например, если объект представляет собой круглое отверстие, результирующее изображение будет пятном Эйри .

Дифракция света на объекте создает его преобразование Фурье либо на бесконечности, либо в фокальной плоскости линзы, называемой плоскостью Фурье .

Фокальная плоскость линзы, где формируется преобразование Фурье объекта, называется плоскостью Фурье .

Интерпретация пространственной частоты

Преобразование Фурье часто используется для анализа спектров , например, в акустике . Действительно, это преобразование позволяет перейти от изучения волны по ее эволюции во времени к изучению ее по частотам . Эти частоты поэтому называются временными , потому что они связаны со временем .

В оптике Фурье преобразование Фурье осуществляется не по времени, а по пространству, а точнее по координатам и в плоскости объекта (определено выше). Поэтому мы определили пространственные частоты, сопряженные с этими координатами. Икс Y

Существует сильная аналогия между временными частотами и пространственными частотами . Например, мы можем получить пространственный спектр, подобный обычному временному спектру : этот пространственный спектр, порождающий пространственные частоты, является пространственным преобразованием Фурье падающей волны. Таким образом, предыдущая часть показывает нам, что плоскость Фурье раскрывает этот спектр. Таким образом, мы визуализируем пространственные частоты в плоскости Фурье .

Таким образом, центр этой плоскости соответствует нулевой пространственной частоте, и чем дальше от этого центра, тем выше соответствующая пространственная частота.

Приложения

Основное применение оптики Фурье - пространственная фильтрация , которая заключается в удалении некоторых пространственных частот с целью изменения изображения объекта. Это приводит к нескольким методам, таким как стриоскопия , лазерная очистка и т. Д.