Доказательство первого признака подобия треугольников 8 класс кратко

Обновлено: 05.07.2024

Дано: АВС и А₁В₁С₁, А = А₁, В = В₁

Доказать: АВСА₁В₁С₁

Доказательство:

По теореме о сумме углов треугольника А +В +С = 180 0 и А₁ +В₁ +С₁ = 180 0 , другими словами, С = 180 0 - А -В и С₁ = 180 0 - А₁ -В₁, и, значит, С = С₁. Таким образом,углы треугольника АВС соответственно равны углам треугольника А₁В₁С₁.

Докажем, что стороны треугольника АВС пропорциональны сходственным сторонам треугольника А₁В₁С₁. Так как А = А₁ и С = С₁, то ,

Так как А = А₁ и В = В₁, то

Итак, стороны треугольника АВС пропорциональны сходственным сторонам треугольника А₁В₁С₁. Теорема доказана.

I. Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.

II. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то такие треугольники подобны.

III. Если три стороны одного треугольника пропорциональны трём сторонам другого, то такие треугольники подобны.

Признаки подобия позволяют сделать вывод о подобии треугольников, не используя при этом все элементы треугольников. На этом уроке мы рассмотрим первый признак подобия треугольников, который позволяет сделать вывод о подобии треугольников по двум равным углам. Также мы докажем этот признак подобия и решим с помощью него несколько типовых задач.

На этом уроке мы сформулируем и докажем первый признак подобия треугольников. Убедимся, что прямая, параллельная одной из сторон треугольника, отсекает от него треугольник, подобный данному. А также, что прямоугольные треугольники подобны по острому углу. Кроме этого решим задачи на закрепление нового материала.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.

Получите невероятные возможности

Конспект урока "Первый признак подобия треугольников"

Вспомним, что подобными называются треугольники, у которых углы соответственно равны, а сходственные стороны пропорциональны.

На одном из предыдущих уроков мы отмечали, что подобие треугольников можно установить, проверив только некоторые из равенств. И сейчас мы познакомимся с первым признаком подобия треугольником.

Теорема (1-й признак подобия треугольников). Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.

Доказательство.

, .

, , ,

, следовательно, .

Так как , то .

, .

Так как , то .

, .

Выше мы доказали, что соответственные углы этих треугольников равны, а значит, они треугольники подобны.

Что и требовалось доказать.

Из доказанной теоремы следует, что прямая, параллельная одной из сторон треугольника, отсекает от него треугольник, подобный данному.

Давайте возьмём некоторый треугольник ABC и проведём прямую MN, параллельную стороне AC.

как соотв. при и секущей ,

Также из доказанного признака следует, что прямоугольные треугольники подобны по острому углу.

А теперь давайте посмотрим на следующие треугольники и найдём среди них подобные.

Итак, треугольники а и в подобны по первому признаку, так как два угла одного треугольника соответственно равны двум углам другого треугольника.

Треугольники д и е являются подобными, так как они прямоугольные и у них острые углы равны.

И у нас остались треугольники б и г. Так как сумма углов треугольника равна ста восьмидесяти градусам, то несложно найти градусную меру третьего угла треугольника б. Она равна 40º. А тогда эти треугольники подобны по двум углам, то есть по первому признаку.

Задача. На стороне параллелограмма отмечена точка . Прямые и пересекаются в точке . Найдите и , если см, см, см, см.

Рассмотрим и .

как вертикальные, как внутр. накрест лежащие при и секущей .

, то есть .

, , (см).

Ответ: см; см.

Задача. На рисунке см, см, см, а . Найдите .

Рассмотрим и .

по условию задачи, – общий.

, , (см).

Итак, на уроке мы доказали первый признак подобия треугольников: если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.

Убедились, что прямая, параллельная одной из сторон треугольника, отсекает от него треугольник, подобный данному. А также, что прямоугольные треугольники подобны по острому углу.

Определение 1. Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого треугольника.

Определение 2. Сходственными называются стороны подобных треугольников, лежащих напротив равных углов.

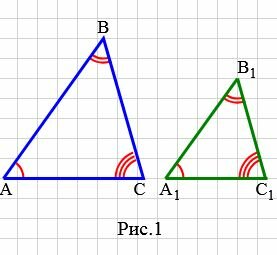На рисунке 1 углы треугольников \( \small ABC \) и \( \small A_1B_1C_1 \) соответственно равны:

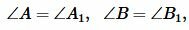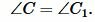(1)

Тогда стороны \( \small AB \) и \( \small A_1B_1 \), \( \small BC \) и \( \small B_1C_1 \), \( \small AC \) и \( \small A_1C_1 \) называются сходственными.

Определение 1 можно понимать так: два треугольника подобны, если для них можно ввести обозначения и (Рис.1) так, что

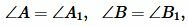Если два треугольника и подобны, то это обозначают так:

Коэффициент подобия треугольников

Коэффициентом подобия треугольников k − это число, равное отношению сходственных сторон (см. формулу (2)).

Перый признак подобия треугольников

Теорема 1. Если два угла одного треугольника соответсвенно равны двум углам другого треугольника, то такие треугольники подобны.

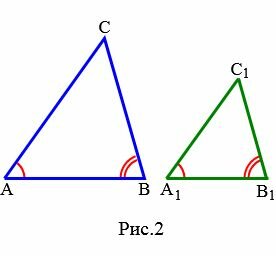Доказательство. Пусть заданы два треугольника и и пусть , . Докажем, что (Рис.2).

Поскольку сумма углов треугольника равна 180°, то можно записать:

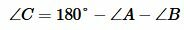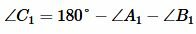и, так как , , получим:

Таким образом углы треугольника соответственно равны углам треугольника . Покажем, теперь, что стороны одного треугольника пропорциональны сходственным сторонам другого треугольника, т. е. выполнено равенство (2).

Площади треугольников и по двум сторонам и углу между ними можно вычислить формулами:

Из (3) и (4), и из следует:

С другой стороны:

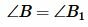
Из (6) и (7), и из следует:

Левые части уравнения (5) и (8) равны. Следовательно равны и правые части:

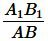
Умножая левую и правую части уравнения (9) на , получим:

Продолжая аналогичные рассуждения, получим:

Сравнивая (8) и (11), получим:

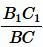
Умножая левую и правую части уравнения (12) на , получим:

Из (10) и (13), получим:

То есть стороны треугольника пропорциональны сходственным сторонам треугольника . Что и требовалось доказать.

Второй признак подобия треугольников

Теорема 2. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы между этими сторонами равны, то такие треугольники подобны.

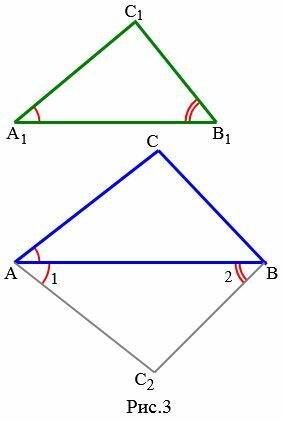Доказательство. Пусть заданы два треугольника и и пусть , . Докажем, что (Рис.3).

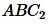
Рассмотрим треугольник у которого

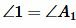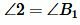(15)

Из условия (15) следует, что треугольники и подобны (по первому признаку подобия треугольников). Следовательно:

Но по условию теоремы . Поэтому . Треугольники и равны по двум сторонам и углу между ними (сторона AB общая, , (поскольку и )). Следовательно и поскольку , то .

Получили, что и . Тогда по первому признаку подобия треугольников .

Третий признак подобия треугольников

Теорема 3. Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.

Доказательство. Пусть стороны треугольников пропорциональны:

Докажем, что . Рассотрим треугольник у которого , (Рис.3). Треугольники и подобны по первому признаку подобия треугольников. Тогда выполнено следующее равенство:

Сравнивая равенства (16) и (17) получаем: , .

Из этих рассуждений следует, что треугольники и равны по трем сторонам (см. статью Треугольники. Признаки равенства треугольников). Тогда , а поскольку , то . Следовательно, по второму признаку подобия треугольников, треугольники и подобны: .

Отношение площадей подобных треугольников

Теорема 4. Отношение площадей подобных треугольников равно квадрату коэффициента подобия.

Доказательство. Пусть треугольники и подобны. Тогда

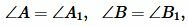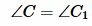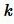
где -коэффициент подобия.

Читайте также: