Частные производные высших порядков кратко
Обновлено: 07.07.2024
На данном уроке мы продолжим знакомство с функцией двух переменных и рассмотрим, пожалуй, самое распространенное тематическое задание – нахождение частных производных первого и второго порядка, а также полного дифференциала функции. Студенты-заочники, как правило, сталкиваются с частными производными на 1 курсе во 2 семестре. Причем, по моим наблюдениям, задание на нахождение частных производных практически всегда встречается на экзамене.
Быстренько повторим понятие функции двух переменных, я постараюсь ограничиться самым минимумом. Функция двух переменных обычно записывается как , при этом переменные , называются независимыми переменными или аргументами.
Пример: – функция двух переменных.
Иногда используют запись . Также встречаются задания, где вместо буквы используется буква .
Для частных производных справедливы все правила дифференцирования и таблица производных элементарных функций. Есть только пара небольших отличий, с которыми мы познакомимся прямо сейчас:
Найти частные производные первого и второго порядка функции
Сначала найдем частные производные первого порядка. Их две.
Комментарии к выполненным действиям:
(1) Первое, что мы делаем при нахождении частной производной – заключаем всю функцию в скобки под штрих с подстрочным индексом.
Далее данный шаг комментироваться не будет, все сделанные замечания справедливы для любого примера по рассматриваемой теме.
(3) Используем табличные производные и .
(1) Используем те же правила дифференцирования , . В первом слагаемом выносим константу за знак производной, во втором слагаемом ничего вынести нельзя поскольку – уже константа.
В чём смысл частных производных?
! Примечание: здесь подразумеваются направления, которые параллельны координатным осям.
Систематизируем элементарные прикладные правила:
1) Когда мы дифференцируем по , то переменная считается константой.
2) Когда же дифференцирование осуществляется по , то константой считается .
3) Правила и таблица производных элементарных функций справедливы и применимы для любой переменной (, либо какой-нибудь другой), по которой ведется дифференцирование.
Шаг второй. Находим частные производные второго порядка. Их четыре.
Со второй производной нет никаких проблем. Говоря простым языком, вторая производная – это производная от первой производной.
Для удобства я перепишу уже найденные частные производные первого порядка:
Сначала найдем смешанные производные:
В практических примерах можно ориентироваться на следующее равенство:
Таким образом, через смешанные производные второго порядка очень удобно проверить, а правильно ли мы нашли частные производные первого порядка.
Следует отметить, что при нахождении , нужно проявить повышенное внимание, так как никаких чудесных равенств для их проверки не существует.
Вторые производные также находят широкое практическое применение, в частности, они используются в задаче отыскания экстремумов функции двух переменных. Но всему своё время:
Вычислить частные производные первого порядка функции в точке . Найти производные второго порядка.
Набиваем руку на более сложных примерах:
Найти частные производные первого порядка функции . Проверить, что . Записать полный дифференциал первого порядка .
Решение: Находим частные производные первого порядка:
(1) Выносим все константы за знак производной. В данном случае и , а, значит, и их произведение считается постоянным числом.
(2) Не забываем, как правильно дифференцировать корни.
(1) Выносим все константы за знак производной, в данной случае константой является .
(2) Под штрихом у нас осталось произведение двух функций, следовательно, нужно использовать правило дифференцирования произведения .
(3) Не забываем, что – это сложная функция (хотя и простейшая из сложных). Используем соответствующее правило: .
Теперь находим смешанные производные второго порядка:
, значит, все вычисления выполнены верно.
Запишем полный дифференциал . В контексте рассматриваемого задания не имеет смысла рассказывать, что такое полный дифференциал функции двух переменных. Важно, что этот самый дифференциал очень часто требуется записать в практических задачах.
Полный дифференциал первого порядка функции двух переменных имеет вид:
В данном случае:
То есть, в формулу нужно тупо просто подставить уже найденные частные производные первого порядка. Значки дифференциалов и в этой и похожих ситуациях по возможности лучше записывать в числителях:
И по неоднократным просьбам читателей, полный дифференциал второго порядка.
Он выглядит так:
Ничего страшного, если что-то показалось трудным, к производным всегда можно вернуться позже, после того, как поднимите технику дифференцирования:
Найти частные производные первого порядка функции . Проверить, что . Записать полный дифференциал первого порядка .
Это пример для самостоятельного решения. Полное решение и образец оформления задачи – в конце урока.
Рассмотрим серию примеров со сложными функциями:
Найти частные производные первого порядка функции .
Записать полный дифференциал .
(1) Применяем правило дифференцирования сложной функции . С урока Производная сложной функции следует помнить очень важный момент: когда мы по таблице превращаем синус (внешнюю функцию) в косинус, то вложение (внутренняя функция) у нас не меняется.
(2) Здесь используем свойство корней: , выносим константу за знак производной, а корень представляем в нужном для дифференцирования виде.
Запишем полный дифференциал первого порядка:
Найти частные производные первого порядка функции .
Записать полный дифференциал .
Это пример для самостоятельного решения (ответ в конце урока). Полное решение не привожу, так как оно достаточно простое
Довольно часто все вышерассмотренные правила применяются в комбинации.
Найти частные производные первого порядка функции .
(1) Используем правило дифференцирования суммы
Для тех читателей, которые мужественно добрались почти до конца урока, расскажу старый мехматовский анекдот для разрядки:
Однажды в пространстве функций появилась злобная производная и как пошла всех дифференцировать. Все функции разбегаются кто куда, никому не хочется превращаться! И только одна функция никуда не убегает. Подходит к ней производная и спрашивает:
– А почему это ты от меня никуда не убегаешь?
На что злобная производная с коварной улыбкой отвечает:
Найти частные производные первого порядка функции .
Это пример для самостоятельного решения. Полное решение и образец оформления задачи – в конце урока.
Ну вот почти и всё. Напоследок не могу не обрадовать любителей математики еще одним примером. Дело даже не в любителях, у всех разный уровень математической подготовки – встречаются люди (и не так уж редко), которые любят потягаться с заданиями посложнее. Хотя, последний на данном уроке пример не столько сложный, сколько громоздкий с точки зрения вычислений.
Дана функция двух переменных . Найти все частные производные первого и второго порядков.
Это пример для самостоятельного решения. Полное решение и образец оформления где-то рядом.
Что дальше? Дальше знакомимся с родственной темой – частными производными функции трёх переменных. После этого я рекомендую ДОБРОСОВЕСТНО (жить будет легче ;)) отработать технику дифференцирования на уроках Производные сложных функций нескольких переменных, Как проверить, удовлетворяет ли функция уравнению? и Частные производные неявно заданной функции. И, наконец, обещанная вкусняшка – Производная по направлению и градиент функции. Стратегия и тактика знакомы – сначала учимся решать, затем вникаем в суть!
Решения и ответы:
Пример 4: Ссылка для просмотра или скачивания ниже.
Автор: Емелин Александр
(Переход на главную страницу)
cкидкa 15% на первый зaкaз, при оформлении введите прoмoкoд: 5530-hihi5

Чтобы понять частные производные, сначала нужно разобраться с обычными. И не нужно ничего искать: в нашей отдельной статье мы уже подготовили все для того, чтобы у вас это получилось. А сейчас речь пойдет о частных производных.
Функция двух и более переменных
Прежде чем говорить о частных производных, нужно затронуть понятие функции нескольких переменных, без которого нет смысла в частной производной. В школе мы привыкли иметь дело с функциями одной переменной:
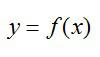
Производными таких функций мы и считали раньше. График функции одной переменной представляет собой линию на плоскости: прямую, параболу, гиперболу и т.д.
А что, если добавить еще одну переменную? Получится такая функция:
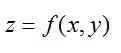
Это – функция двух независимых переменных x и y. График такой функции представляет собой поверхность в трехмерном пространстве: шар, гиперболоид, параболоид или еще какой-нибудь сферический конь в вакууме. Частные производные функции z по иксу и игреку соответственно записываются так:
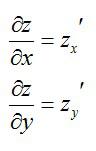
Существуют также функции трех и более переменных. Правда, график такой функции нарисовать невозможно: для этого понадобилось бы как минимум четырехмерное пространство, которое невозможно изобразить.
Частная производная первого порядка
Запоминаем главное правило:
При вычислении частной производной по одной из переменных, вторая переменная принимается за константу. В остальном правила вычисления производной не меняются.
То есть, частная производная по сути ничем не отличается от обычной. Так что, держите перед глазами таблицу производных элементарных функций и правила вычисления обычных производных. Рассмотрим пример, чтобы стало совсем понятно. Допустим, нужно вычислить частные производные первого порядка следующей функции:
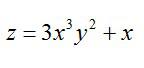
Сначала возьмем частную производную по иксу, считая игрек обычным числом:
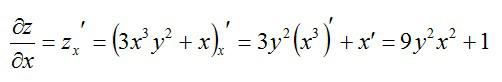
Теперь считаем частную производную по игреку, принимая икс за константу:
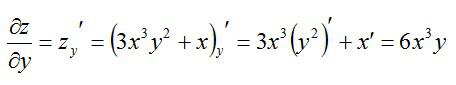
Как видите, ничего сложного в этом нет, а успех с более сложными примерами – лишь дело практики.
Частная производная второго порядка
Как находится частная производная второго порядка? Так же, как и первого. Чтобы найти частные производные второго порядка, нужно просто взять производную от производной первого порядка. Вернемся к примеру выше и посчитаем частные производные второго порядка.
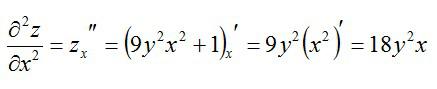
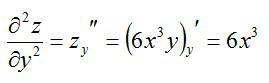
Частные производные третьего и высших порядков не отличаются по принципу вычисления. Систематизируем правила:
- При дифференцировании по одной независимой переменной, вторая принимается за константу.
- Производная второго порядка – это производная от производной первого порядка. Третьего порядка – производная от производной второго порядка и т.д.
Частные производные и полный дифференциал функции
Частый вопрос в практических заданиях – нахождение полного дифференциала функции. Для функции нескольких переменных полный дифференциал определяется, как главная линейная часть малого полного приращения функции относительно приращений аргументов.
Определение звучит громоздко, но с буквами все проще. Полный дифференциал первого порядка функции нескольких переменных выглядит так:
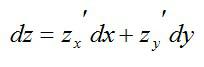
Зная, как считаются частные производные, нет никакой проблемы вычислить и полный дифференциал.
Частные производные – не такая уж и бесполезная тема. Например, дифференциальные уравнения в частных производных второго порядка широко используются для математического описания реальных физических процессов.
Здесь мы дали лишь общее, поверхностное представление о частных производных первого и второго порядка. Вас интересует эта тема или остались конкретные вопросы? Задавайте их в комментариях и обращайтесь к экспертам профессионального студенческого сервиса за квалифицированной и скорой помощью в учебе. С нами вы не останетесь один на один с проблемой!
Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.
Пусть во всех точках открытого множества \(G\subset R^3\) существует частная производная \(\partial f(x)/\partial x_i\). Эта производная как функция \(x\) может иметь в некоторой точке \(x^0\) производную
$$
\frac<\partial><\partial x_j>\left(\frac<\partial f><\partial x_i>\right)_,\nonumber
$$
которая называется частной производной второго порядка и обозначается одним из символов
$$
\frac<\partial^2 f><\partial x_i \partial x_j>(x^0),\quad f_(x^0),\quad D_(x^0), \frac<\partial^2 f(x^0)><\partial x_i \partial x_j>.\nonumber
$$
Если \(i=j\), то для частной производной применяется обозначение
$$
\frac<\partial^2 f(x^0)><\partial x_i^2>.\nonumber
$$
Производные \(f_(x,y)\) и \(f_(x,y)\) называют смешанными. Вообще говоря, они могут быть неравны.
Покажем, что \(f_(0,0)\neq f(yx)(0,0)\).
Теорема о смешанных производных.
Если обе смешанные производные \(f_(x,y)\) и \(f_(x,y)\) определены в некоторой окрестности точки \((x_0,y_0)\) и непрерывны в этой точке, то \(f_(x_0,y_0)=f_(x_0,y_0)\).
\(\circ\) Пусть смешанные производные определены в прямоугольнике \(\Pi=\
Поскольку для функции \(n\) переменных \(f(x_1,\ldots,x_n)\) при вычислении смешанных производных \(\partial^2 f/\partial x_i \partial x_j\) и \(\partial^2 f/\partial x_j \partial x_i\) все переменные, кроме \(x_i\) и \(x_j\), фиксируются, то фактически рассматривается функция только двух переменных и обе смешанные производные в точке \(x^0\) равны, если они в этой точке непрерывны.
По индукции легко доказать, что если производная \eqref и все производные порядка \(m\), которые получаются при помощи всевозможных перестановок индексов \(i_1,i_2,\ldots,i_m\), определены в окрестности точки \(x^0\) и непрерывны в точке \(x^0\), то все эти производные равны в точке \(x^0\). Если вспомнить, что транспозицией называется такая перестановка, которая переставляет два соседних элемента, а все остальные оставляет на своих местах, то легко понять, что две производные \(m\)-го порядка, полученные при помощи транспозиции индексов, будут равны по теореме 1 о смешанной производной. В курсе алгебры доказывается, что все перестановки можно упорядочить таким образом, что каждая последующая перестановка получается из предыдущей при помощи транспозиции. Упорядочивая таким же образом и все производные \(m\)-го порядка, получающиеся перестановкой индексов, заключаем, что все они равны.
Дифференциалы высших порядков.
Пусть функция \(u(x)\) имеет в области \(G\subset R^n\) непрерывные частные производные первого и второго порядков. Тогда дифференциал
$$
du(x)=\sum_^n\frac<\partial u><\partial x_i>(x)dx_i,\qquad x\in G,\nonumber
$$
есть функция \(2n\) переменных, а именно \(x_1,…,x_n\) и \(dx_1,…,dx_n\).
Если фиксировать переменные \(dx_1,…,dx_n\), то дифференциал \(du(x)\) будет функцией \(x\), имеющей в области \(G\) непрерывные частные производные. \(du(x)\) как функция \(x\) имеет в каждой точке \(x\in G\) дифференциал \(d(du)\). Если приращения независимых переменных обозначить через \(\delta x_1,…,\delta x_n\), то
$$
d(du(x))=\sum_^n\frac\partial<\partial x_k>(du(x))\delta x_k=\sum_^n\sum_^n\frac<\partial^2u(x)><\partial x_k\partial x_i>dx_i\delta x_k.\label
$$
Выражение \(d(du(x))\) есть билинейная форма относительно приращений \(dx_1,\delta x_1,…,dx_n,\delta x_n\). Полагая в этой билинейной форме \(dx_1=\delta x_1,…,dx_n=\delta x_n\), получаем квадратичную форму, которая называется вторым дифференциалом функции \(u(x)\) в точке \(x\) и обозначается через \(d^2u(x)\). Таким образом,
$$
d^2u(x)=\sum_^n\sum_^n\frac<\partial^2u(x)><\partial x_i\partial x_k>dx_i d x_k.\label
$$
Аналогично, предполагая, что все частные производные третьего порядка непрерывны, можно вычислить первый дифференциал от \(d^2u(x)\), после чего положить \(\delta x_i=dx_i\) и полученную однородную форму третьего порядка назвать третьим дифференциалом функции \(u(x)\). Третий дифференциал обозначается через \(d^3u(x)\). Таким образом,
$$
d^3u(x)=\sum_^n\sum_^n\sum_^n\frac<\partial^3u(x)><\partial x_i\partial x_j\partial x_k>dx_i \ d \ x_j \ dx_k.\nonumber
$$
По индукции определяется дифференциал \(m\)-го порядка в предположении, что все частные производные \(m\)-го порядка непрерывны в точке \(x\). Если дифференциал \(d^u(x)\) вычислен как однородная форма порядка \(m-1\) относительно \(dx_1,…,dx_n\) с коэффициентами, являющимися функциями \(x\), то, вычисляя первый дифференциал от \(d^u(x)\) и полагая затем \(\delta x_i=dx_i\) при \(i=\overline\), получим, что \(d^u(x)\) есть однородная форма порядка \(m\), то есть
$$
d^u(x)=\sum_^n\ldots\sum_^n\frac<\partial^u(x)><\partial x_\ldots\partial x_>dx_\ldots dx.\nonumber
$$
Покажем, что дифференциал второго порядка уже не обладает свойством инвариантности относительно замены переменных. Пусть \(f(x)=f(x_1,\ldots,x_n), \ x_i=\varphi_i(u), \ u\in R^m\), функции \(f(x)\) и \(\varphi(u)\) имеют все непрерывные частные производные до второго порядка включительно и сложная функция \(f(\varphi(u),\ldots,\varphi(u))\) определена в некоторой окрестности точки \(u\). Тогда в силу инвариантности формы первого дифференциала получаем равенство
$$
df(x(u))=\sum_^n\frac<\partial f><\partial x_i>(x)dx_i(u).\nonumber
$$
Пользуясь правилом нахождения дифференциала произведения и суммы, получаем
$$
d^2f(x(u))=\sum_^nd\left(\frac<\partial f><\partial x_i>(x(u))dx_i(u)\right)=\sum_^n\sum_^n\frac<\partial^2f(x(u))><\partial x_i\partial x_j>dx_idx_j+\sum_^n\frac<\partial f(x(u))><\partial x_i>d^2x_i.\label
$$
Формула (\eqref отличается от формулы \eqref наличием суммы
$$
\sum_^n\frac<\partial f(x)><\partial x_i>d^2x_i.\nonumber
$$
которая обращается в нуль, если \(x_1,\ldots,x_n\) — независимые переменные.
Если замена переменных линейная, то \(d^2x_i=0, \ i=\overline\). Таким образом, второй дифференциал \(d^2f(x)\) инвариантен относительно линейной замены переменных. То же самое справедливо и для дифференциалов всех порядков.
Если ввести формально дифференциальный оператор
$$
d=\sum_^dx_i\frac<\partial><\partial x_i>,\label
$$
то выражения для дифференциалов можно записать в удобной символической форме:
$$
\begind^2u(x)=(d^2)u(x)=\displaystyle\left(\sum_^ndx_i\frac\partial<\partial x_i>\right)^2u(x),\\d^mu(x)=(d^m)u(x)=\displaystyle\left(\sum_^dx_i\frac\partial<\partial x_i>\right)^mu(x).\end\nonumber
$$
Под произведением дифференциальных операторов понимается их последовательное применение. Например, если \(D_i=\partial/\partial x_i\), то
$$
(D_iD_j)u=D_i(D_ju)=\frac\partial<\partial x_i>\left(\frac<\partial u><\partial x_j>\right)=\frac<\partial^2u><\partial x_j\partial x_i>,\quad D_iD_j=\frac<\partial^2><\partial x_j\partial x_i>.\label
$$
При перемножении дифференциальных операторов вида \eqref нужно пользоваться правилом \eqref. При этом дифференциалы независимых переменных \(dx_1,…,dx_n\) перемножаются как вещественные числа.
Рассмотрим функцию двух переменных n =2, . Предположим, что функция имеет частные производные
которые являются функциями двух переменных. Их называют частными производными первого порядка. Предположим, что они дифференцируемы.
Определение 1. Частные производные от частных производных первого порядка называются частными производными второго порядка.
Две последние называют смешанными производными.
Если полученные функции являются дифференцируемыми, то частные производные от них называются частными производными третьего порядка. Например:
Определение 2. Частной производной n-го порядка называется частная производная от частной производной (n-1)-го порядка. Частных производных n-го порядка от функции двух переменных 2 n штук.
Частная производная порядка р функции имеет вид
Теорема. Если частные производные первого порядка некоторой функции непрерывно дифференцируемы, то результаты смешанного дифференцирования равны.
Читайте также:

