Выбор точки из фигуры на плоскости конспект
Обновлено: 02.07.2024
Цель урока: ввести определение геометрической вероятности
Задачи: рассмотреть определение геометрической вероятности при выборе точки из фигуры на плоскости, при выборе точки из отрезка, из дуги окружности, при выборе точки из числового отрезка; добиться качественного понимания этого определения; научиться применять его при решении задач.
Тип урока: лекционно-семинарский
Формы работы учащихся: фронтальная, индивидуальная
Организационный момент формулирование темы урока
Постановка задачи (этап – “интрига”)
Учитель просит учеников дать классическое определение вероятности и предлагает задачу.
Задача о монете.
На тетрадный лист в линейку наудачу бросается рублевая монета. Расстояние между линейками равно 8 мм, диаметр монеты 20 мм. Какова вероятность того, что монета пересечет
а) две линии б) три линии?
Ученики должны рассмотреть все возможные элементарные события в этом опыте и убедиться, что монета пересекает 2 или 3 линии. Важно подвести учеников к мысли, что исходы опыта можно связать с расстоянием от центра монеты до ближайшей линейки.
Результатом работы с этой моделью должно быть, что количество возможных исходов (элементарных событий) в этом опыте бесконечно много! Это числа из отрезка [0; 4]. Благоприятствующих элементарных событий, соответствующих а) и б) тоже бесконечно много…
КАК ПОСЧИТАТЬ ВЕРОЯТНОСТЬ?
Геометрическое определение вероятности при выборе точки из фигуры на плоскости
Ученикам предлагается рассмотреть следующую задачу (фронтальная работа с обсуждением, причем учителю следует вводить определение после попыток учеников самостоятельно ответить на вопрос задачи).
Точку наудачу бросают в область F на плоскости. Какова вероятность того, что точка попадет в некоторую область G, которая содержится в фигуре F?
Если предположить, что попадание в любую точку области F равновозможно, то вероятность попадания случайной точки в область G будет равна отношению площадей области G и области F, то есть
Такое определение вероятности называется геометрическим.
Заметим, что площадь фигуры G не больше, чем площадь фигуры F, поэтому P (A)≤1.
Имеет смысл после введения определения поработать над качественным пониманием его, предложив следующий пример:
Выберем на географической карте мира случайную точку (зажмурили глаза и показали указкой).
- Какова вероятность что эта точка окажется в России? (Для ответа на вопрос нужно знать какую часть всей карты занимает Россия)
- Какова вероятность попасть в Гринвичский меридиан (Как ни странно, придется положить ее равной 0, так как площадь меридиана равна 0 – попасть указкой точно в меридиан невозможно)
4. Решение задач
Точку наудачу бросают в квадрат, сторона которого равна 1. Какова вероятность того, что расстояние от этой точки до ближайшей стороны квадрата не больше, чем
Решение этой задачи провести при фронтальном обсуждении его. У доски может работать ученик или учитель (зависит от подготовленности аудитории)
SF=1 (площадь исходного квадрата)
Точка удалена от границы квадрата не более чем на , если она попала в заштрихованную на рисунке фигуру G.
SG = SF – SABCD = 1 - =
Ученикам предлагается самостоятельно по вариантам решить следующие задачи:
В квадрате случайным образом берется точка. Найдите вероятность того, что эта точка не принадлежит вписанному в этот квадрат кругу.
В круге случайным образом берется точка. Найдите вероятность того, что эта точка принадлежит вписанному в этот круг квадрату.
После решения эти задачи необходимо проверить и обсудить решения (слайд презентации, или подготовленная запись решения на откидной доске)
Пусть сторона квадрата равна a, тогда r = a
SA – площадь заштрихованной области квадрата
SA = Sкв - Sкр = a2 - πa2 = a2
Пусть радиус круга равен a.
Если темп урока позволяет, имеет смысл задать дополнительные вопросы по этим задачам (вероятности попадания в другие, указанные учителем, области)
Геометрическое определение вероятности при выборе точки из отрезка, дуги окружности; при выборе точки из числового отрезка
Пусть отрезок CD содержится в отрезке MN. Нас интересует событие A, состоящее в том, что выбранная точка X принадлежит отрезку CD.
Аналогично определению геометрической вероятности данному выше имеем
Учителю стоит обратить внимание учеников на аналогию рассматриваемого примера с приведенным выше. Отличие состоит только в мерности объектов. И опять следует подчеркнуть, что P (A) – число неотрицательное и не превосходящее 1, как и полагается для вероятности случайного события. Далее предлагается пример для фронтальной работы с ним. Пример предлагается ученикам как задача. Цель работы с ним – качественное понимание данного определения. Не стоит давать рисунок вместе с текстом, так как в нем содержится подсказка.
Внутри отрезка MN случайным образом выбирается точка X. Найдите вероятность того, что точка X ближе к N чем к M.
Пусть O – середина отрезка MN. Обозначим указанное событие через A. Это событие наступит только тогда, когда точка X лежит внутри отрезка ON. То есть P (A) = =
Ничего не меняется, если точка X выбирается не из отрезка, а из дуги некоторой кривой линии. Например, можно случайным образом выбирать точку X на окружности.
Пример: в окружность вписан квадрат ABCD. На окружности случайным образом выбирается точка M. Найдите вероятность того, что эта точка лежит на:
а) меньшей дуге AB
б) большей дуге AB
Учитель предлагает ученикам самостоятельно решить эту задачу. Проверка с помощью слайда или рисунка, заранее подготовленного на откидной доске.
A – указанное событие
5.3 Геометрическую вероятность можно применять к числовым промежуткам. Предположим, что случайным образом выбирается число x, удовлетворяющее условию
m ≤ x ≤ n. Этот опыт можно заменить опытом, в котором из отрезка [m; n] на числовой прямой выбирается точка с координатой x.
Рассмотрим событие, состоящее в том, что точка с координатой x выбирается из отрезка
[a; b], содержащегося в отрезке [m; n].
Это событие обозначим (a ≤ x ≤ b). Его вероятность равна отношению длин отрезков [a; b] и [m; n].
Найти вероятность того, что точка, случайно выбранная из отрезка [0; 1], принадлежит отрезку []
Учитель подводит итог на этом этапе урока, задавая ученикам следующие вопросы:
- с какой вероятностью познакомились на этом уроке?
- для каких случаев была рассмотрена эта вероятность?
Учитель еще раз обращает внимание учеников на аналогичность определения геометрической вероятности во всех случаях и возвращает к началу урока, к задаче о монете, предлагая ученикам теперь ее решить.
Решение задачи о монете
Вспомним, что положение монеты договорились оценивать по расстоянию от центра монеты до ближайшей линейке. Если обозначить это расстояние x, то множество всех исходов соответствует 0 ≤ x 4. Монета бросается на лист наудачу, это значит что все значения x из отрезка [0; 4] будут равновозможными.
Учебно-методические пособия и материалы для учителей, 2015-2022
Все материалы взяты из открытых источников сети Интернет. Все права принадлежат авторам материалов.
По вопросам работы сайта обращайтесь на почту [email protected]
- Для учеников 1-11 классов и дошкольников
- Бесплатные сертификаты учителям и участникам
Конспект урока по теме : Геометрическая вероятность.
Выбор точки из фигуры на плоскости.
Цели урока :
Развивающие : развитие зрительной памяти, математически грамотной речи, логического мышления, сознательного восприятия учебного материла, закрепление интереса к предмету, мотивации к учению;
Воспитательные : воспитание познавательной активности, культуры общения, культуры диалога.
Оборудование:
Ход занятия.
I. Организационный момент:
цели и задачи занятия, исходная мотивация, психологический настрой учащихся на занятие и личность учителя, план урока.
II. Изучение нового материала.
Этот этап урока можно провести в форме фронтального опроса .
Вопрос. Чему равна вероятность?
Ответ. Вероятность равна отношению благоприятных исходов к общему числу исходов.
Вопрос. Рассмотрим ситуацию. Точку наудачу бросают в фигуру В на плоскости. Как вы думаете, как определить вероятность попадания точки в область А по данному чертежу ?
Ответ. Вероятность попадания точки в область А равна отношению площадей области А к области В.
Учитель. В этой задаче речь идёт о так называемой геометрической вероятности. Задачи, в которых используется данная вероятность, относятся к разным направлениям человеческой деятельности. Это астрономия и сельское хозяйство, геология и военное дело, и т.д.
III. Первичная проверка понимания нового материала.
Вопрос. Рассмотрим несколько устных задач. Чему будет равна вероятность попадания точки в область А в предложенных заданиях?
Испытанием называется осуществление определенных действий.
Под событием понимают любой факт, который может произойти в результате испытания.
Любой результат испытания называется исходом.
Достоверным называют событие, которое в результате испытания обязательно произойдёт.
Невозможным называют событие, которое заведомо не произойдёт в результате испытания.
Геометрической вероятностью некоторого события называется отношение P(A) = g/G, где G – геометрическая мера, выражающая общее число всех равновозможных исходов данного испытания, а g – мера, выражающая количество благоприятствующих событию A исходов
Основная литература:
Виленкин Н. Я., Ивашев-Мусатов О. С., Шварцбурд С. И. Алгебра и математический анализ для 11 класса: Учеб. пособие для учащихся шк. и классов с углубл. изуч. математики. - 4-е изд. - М.: Просвещение, 1995. - 288 с.: ил. - ISBN 5-09-0066565-9. сс.253-259.
Открытые электронные ресурсы:
Теоретический материал для самостоятельного изучения
Вероятность наступления некоторого события A в испытании равна P(A) = g/G, где G – геометрическая мера, выражающая общее число всех равновозможных исходов данного испытания, а g – мера, выражающая количество благоприятствующих событию A исходов.

Рисунок 1 - иллюстрация геометрической вероятностей
Пусть отрезок l составляет часть отрезка L. На отрезок L наудачу поставлена точка. Вероятность попадания точки на отрезок l равна P(A) = |l|/|L|.
Пусть пространственная фигура d составляет часть фигуры D. В фигуру D наудачу ставится точка. Вероятность попадания точки в фигуру d равна P(A) = V(d)/V(D).
Пример использования геометрического определения вероятности при решении задачи.
Два друга договорились встретиться в определенном месте между 12 и 13 часами. Пришедший первым ждет другого в течении 20 минут, после чего уходит. Чему равна вероятность встречи друзей, если приход каждого из них может произойти
наудачу в течении указанного часа и моменты прихода независимы?
х - момент прихода первого друга
y - момент прихода второго друга

Рисунок 2 - Иллюстрация к задаче
S=60 2 –2·1/2·40 2 =2000
P(A) = 2000/60 2 = 5/9.
Ответ: вероятность встречи 5/9.
Примеры и разбор решения заданий тренировочного модуля
Пример 1. Метровый шнур случайным образом разрезают ножницами. Найти вероятность того, что длина обрезка составит не менее 80 см.
Общему числу исходов соответствует длина шнура 1 м. Чтобы длина обрезка составила не менее 0,8 м, можно отрезать не более 0,2 м. Такие отрезы можно выполнить с любой стороны шнура, их суммарная длина равна 0,2+0,2=0,4 м. По геометрическому определению:
Пример 2. В шар брошена случайная точка.
2а) С какой вероятностью она попадёт в центр шара?
Объём одной точки (центра шара) равен нулю, значит и искомая вероятность равна 0
2б) С какой вероятностью она попадёт на какой-нибудь диаметр шара?
Любая точка шара всегда попадает на какой-нибудь диаметр. Поэтому вероятность равна единице.
2в) С какой вероятностью она попадёт в одно, определённое, полушарие?
При решении этой задачи используем отношение объемов фигур. Пусть весь объём шара равен V. Все точки шара - трёхмерная фигура Ω. Искомая вероятность равна отношению объёма полушария V(A) к объёму шара V:


Пример 3. В круг радиуса см вписан равнобедренный прямоугольный треугольник. В круг наудачу ставится точка. Найдите вероятность того, что она не попадёт в данный треугольник. При необходимости в расчетах используйте значение π с точностью до целых.

Площадь круга равна

Гипотенуза прямоугольного треугольника, вписанного в круг, равна диаметру круга (прямой угол опирается на диаметр), то есть .
Поскольку треугольник равнобедренный, его катеты равны между собой, и по теореме Пифагора каждый катет равен . Площадь такого треугольника будет равна (можно найти площадь треугольника, не вычисляя длины катета: рассмотрим квадрат со стороной, равной гипотенузе нашего треугольника, площадь такого квадрата в четыре раза больше площади треугольника
Вероятность попадания точки в треугольник равна отношению площадей треугольника и круга:
За окном ранние осенние деньки, и жёлтая листва на деревьях навевает лирическое и немного грустное настроение…. Но впереди ещё целый учебный год и в такие моменты нужно обязательно настроиться на плодотворную работу! Спешу обрадовать всех хандрящих читателей своим фирменным рецептом, позволяющим быстро повысить тонус своего организма. Для этого достаточно немножко вспомнить геометрию… …нет, я согласен, что иногда она усыпляет, но в небольших дозах – исключительно бодрит! И, главное, очень действенно – как только начинаешь принимать живительные порции знаний, так сразу никакой сезонной депрессии!
Ещё на первом уроке по теме мы познакомились с классическим определением вероятности появления некоторого события в испытании и простейшей формулой , где – общее число всех возможных равновозможных, элементарных исходов данного испытания, а – кол-во элементарных исходов, благоприятствующих событию .
Возникли затруднения с терминологией и/или пониманием? Пожалуйста, начните с основ теории вероятностей.
Едем дальше: классическое определение вероятности оказывается эффективным для решения целого спектра задач, но с другой стороны, обладает и рядом недостатков. Даже правильнее сказать, не недостатков, а ограничений. Одним из таких ограничений является тот факт, что оно неприменимо к испытаниям с бесконечным количеством исходов. Простейший пример:
Всё очень похоже: вероятность наступления некоторого события в испытании равна отношению , где – геометрическая мера, выражающая общее число всех возможных и равновозможных исходов данного испытания, а – мера, выражающая количество благоприятствующих событию исходов. На практике в качестве такой геометрической меры чаще всего выступает длина или площадь, реже – объём.
Рассмотрим событие: – брошенная на отрезок точка, попала в промежуток . Очевидно, что общее число исходов выражается длиной бОльшего отрезка: , а благоприятствующие событию исходы – длиной вложенного отрезка: По геометрическому определению вероятности:
Слишком просто? Как и в случае с классическим определением, это обманчивое впечатление. Обстоятельно и добросовестно разбираемся в практических примерах:
Метровую ленту случайным образом разрезают ножницами. Найти вероятность того, что длина обрезка составит не менее 80 см.
Поскольку ленту можно разрезать где угодно, то общему числу исходов соответствует её длина: Благоприятствующие событию участки разреза отмечены на рисунке красным цветом и их суммарная длина равна: По геометрическому определению:
Ответ: 0,4
Какой можно сделать вывод? Даже если задача кажется вам очень простой, НЕ СПЕШИТЕ. Импульсивность вообще штука скверная – это ошибки, ненужные покупки, испорченные кожные покровы отношения и т.д.… но не будем о грустном!
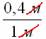
При оформлении задач следует обязательно указывать размерность (единицы, метры, квадратные единицы, квадратные метры и т.д.). Кстати, обратите внимание, что на финальном этапе вычислений геометрическая мера сокращается. Так в рассмотренном примере, сократились метры: , в результате чего получилась привычная безразмерная вероятность.
Разминочная задача из сборника Рябушко:
После бури на участке между 40-м и 70-м километрами телефонной линии произошёл обрыв провода. Какова вероятность того, что он произошёл между 50-м и 55-м километрами линии?
Краткое и решение и ответ в конце урока.
Значительно чаще встречаются примеры, в которых фигурируют площади:
В треугольник со сторонами вписан круг. Точка произвольно ставится в треугольник. Найти вероятность того, что точка попадёт в круг.
Напоминаю, что вписанный круг лежит внутри треугольника и касается его сторон в 3 точках
Решение: поскольку точка ставится в треугольник, а круг лежит внутри, то общему числу исходов соответствует площадь треугольника, а множеству благоприятствующих исходов – площадь вписанного круга. Что тут сказать? Ищем площади:
Если даны длины сторон треугольника, то его площадь удобно найти по формуле Герона:
, где – длины сторон треугольника, а – полупериметр.
Сначала вычислим полупериметр треугольника: , а затем его площадь:
Методику вынесения множителей из-под корня я освещал ещё в древние-древние времена на вводном уроке по аналитической геометрии.
Площадь вписанного круга найдём по формуле , где – его радиус.
Откуда брать геометрические формулы? Нужные формулы можно найти в школьном учебнике или другом источнике информации. При этом нет никакой необходимости специально их разучивать, лично я вспомнил только , а всё остальное в считанные минуты нашёл в Википедии. И через считанные минуты всё это благополучно забуду =)
Итак, площадь вписанного круга:
По геометрическому определению:
– вероятность того, что точка попадёт во вписанный круг.
Ответ:
Более простой пример для самостоятельного решения:
В круге радиуса 10 см находится прямоугольный треугольник с катетами 12 и 7 см. В круг наудачу ставится точка. Найти вероятность того, что она не попадёт в данный треугольник.
Следует отметить, что в этой задаче треугольник вовсе не обязан как-то касаться окружности, он просто расположен внутри круга и всё. Будьте внимательны!
А теперь рассмотрим широко известную задачу о встрече:
Две грузовые машины могут подойти на погрузку в промежуток времени от 19.00 до 20.30. Погрузка первой машины длится 10 минут, второй – 15 минут. Какова вероятность того, что одной машине придется ждать окончания погрузки другой?
Решение: сначала выясняем длительность временнОго промежутка, на котором может состояться встреча. В данном случае, как уже отмечено выше, это полтора часа или 90 минут. При этом здесь не имеют особого значения фактические временнЫе рамки – погрузка автомобилей, может состояться, например, утром с 8.30 до 10.00, и решение будет точно таким же.
Вычисления допустимо проводить как в долях часа, так и в минутах. На мой взгляд, в большинстве случаев удобнее работать с минутами – меньше путаницы.
На первом шаге изобразим прямоугольную систему координат, где в подходящем масштабе построим квадрат размером 90 на 90 единиц; при этом одна из вершин квадрата совпадает с началом координат, а его смежные стороны лежат на координатных осях.
Общему множеству исходов будет соответствовать площадь данного квадрата: Размерность лучше указать в квадратных единицах, поскольку квадратные минуты смотрятся как-то неудачно.
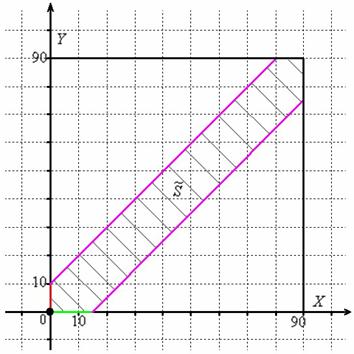
Далее по оси от начала координат откладываем время погрузки одного автомобиля (зелёная линия), а по оси – время погрузки другого автомобиля (красная линия) (можно наоборот, это не повлияет на решение):
Теперь из правого конца зелёного отрезка и из верхнего конца красного отрезка под углом 45 градусов проводим две линии внутри квадрата (малиновые отрезки).
И бесхитростный заключительный манёвр: из площади квадрата вычитаем площади треугольников, получая тем самым благоприятствующую площадь:
По геометрическому определению:
– вероятность того, что одной машине придется ждать окончания погрузки другой.
Ответ:
Если в разобранной задаче встреча была явно нежелательна, то в следующей – скорее, наоборот =) Романтичный эпизод для самостоятельного изучения:
Студенты случайным образом приходят в столовую с 14.00 до 15.00, при этом обед каждого из них занимает примерно 20 минут. Найти вероятность того, что: а) Коля встретится с Олей во время обеда, б) данная встреча не состоится.
Оставшиеся примеры статьи посвящены не менее распространённой задаче на геометрическое определение вероятности. Для начала заманивающий пример:
В квадрат с вершинами наудачу брошена точка . Найдите вероятность того, что координаты этой точки удовлетворяют неравенству.
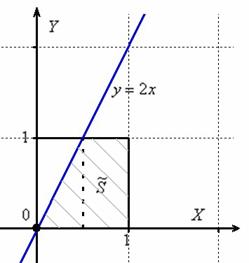
Решение: изобразим на чертеже искомый квадрат и прямую :
Общему множеству исходов соответствует площадь квадрата
Прямая делит квадрат на треугольник и трапецию. Как определить фигуру, которая удовлетворяет условию ? Вспоминаем линейные неравенства: нужно взять любую точку, не принадлежащую прямой , например, точку и подставить её координаты в неравенство:
Получено верное неравенство, значит, множеству благоприятствующих исходов соответствует площадь трапеции. Рассчитаем данную площадь как сумму площадей прямоугольного треугольника и прямоугольника:
По геометрическому определению:
– вероятность того, что координаты брошенной в данный квадрат точки удовлетворяют неравенству.
Ответ:
…я так и знал, что вы соскучились по неравенствам =) А они бывают не только линейными:
Загадываются два числа и в промежутке от 0 до 5. Какова вероятность, что ?
Схема решения уже знакома: коль скоро загадываются 2 произвольных числа от нуля до пяти (они могут быть и иррациональными), то общему количеству исходов соответствует площадь квадрата
Уточним нижний предел интегрирования аналитически (найдём точку пересечения гиперболы и прямой ):
На отрезке прямая расположена не ниже гиперболы ,
по соответствующей формуле:
По геометрическому определению:
– вероятность того, что произведение двух загаданных в промежутке от 0 до 5 чисел окажется больше двух.
Ответ:
Аналогичный пример для самостоятельного решения:
Загадываются два числа и в промежутке от 0 до 10. Какова вероятность, что ?
Данная задача (как, собственно, и предыдущая) допускает несколько способов расчёта площади, подумайте, какой путь более рационален. Моя версия решения совсем близко.
В заключение следует отметить, что геометрическое определение вероятности тоже обладает своими недостатками. Один из них заключается в своеобразном парадоксе, давайте вспомним демонстрационный пример с отрезком , на который случайным образом падает точка. Возможно ли, что точка попадёт, например, на самый край отрезка? Да, такое событие возможно, но по геометрическому определению, его вероятность равна нулю! И то же самое можно сказать о любой точке отрезка! Дело в том, что с позиций геометрии размеры отдельно взятой точки равны нулю, и поэтому геометрическое определение вероятности здесь не срабатывает.
Надеюсь, ваше настроение значительно улучшилось и теперь вы обязательно справитесь со всеми учебными и внеучебными трудностями. …Не улучшилось?! Дополнительные задачи по теме можно найти в архиве готовых решений по сборнику Чудесенко =) =)
Везения в главном!
Решения и ответы:
Задача 2: Решение: используем геометрическое определение вероятности. Общему числу исходов соответствует участок длиной , благоприятствующему количеству исходов – участок длиной . Таким образом:
– вероятность того, что обрыв провода произошёл между 50-м и 55-м километрами линии.
Ответ:
Задача 4: Решение: общему количеству исходов соответствует площадь круга:
Площадь прямоугольного треугольника равна полупроизведению его катетов:
По условию поставленная в круг точка не должна попасть в треугольник, поэтому благоприятствующее число исходов выражается разностью
По геометрическому определению:
– вероятность того, что поставленная в круг точка не попадёт в треугольник.
Ответ:
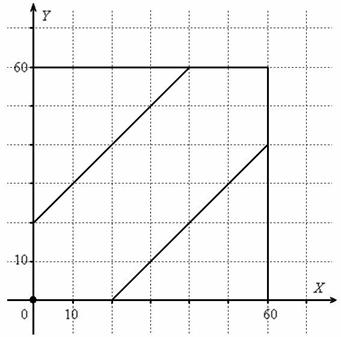
Задача 6: Решение: Оля и Коля могут встретиться в течение 60 минут. Выполним чертёж:
Площадь квадрата соответствует общему числу исходов.
Рассмотрим противоположные события:
– Оля и Коля встретятся во время обеда;
– данной встречи не состоится.
Вычислим суммарную площадь двух треугольников:
– данное значение благоприятствует событию .
По геометрическому определению вероятности:
Противоположные события образуют полную группу, поэтому:
Ответ:
Автор: Емелин Александр
(Переход на главную страницу)
cкидкa 15% на первый зaкaз, при оформлении введите прoмoкoд: 5530-hihi5

Тип урока: урок обобщения и систематизации знаний.
Методы: словесные, наглядные, парные, самостоятельной работы, фронтального опроса, контроля и оценки
Оборудование: интерактивная доска, карточки для самостоятельной работы
Цель: закрепить навыки нахождения координат отмеченных точек и строить точки по заданным координатам. Задачи урока:
- развитие вычислительных навыков обучающихся;
- развитие логического мышления;
- развитие математически грамотной речи, кругозора учащихся;
- развитие умения самостоятельной работы.
- воспитание дисциплинированности при организации работы на уроке;
- воспитание аккуратности при выполнении построений.
Тема "Координатная плоскость. Построение на плоскости точек по заданным координатам".
Абабакарова М.С.
учитель математики
МКОУ «Уркарахская многопрофильная
Тип урока: урок обобщения и систематизации знаний.
Методы: словесные, наглядные, парные, самостоятельной работы, фронтального опроса, контроля и оценки
Оборудование: интерактивная доска, карточки для самостоятельной работы
Цель: закрепить навыки нахождения координат отмеченных точек и строить точки по заданным координатам.
Задачи урока:
Образовательные:
промежуточный контроль знаний и умений учащихся.
Развивающие:
развитие вычислительных навыков обучающихся;
развитие логического мышления;
развитие математически грамотной речи, кругозора учащихся;
развитие умения самостоятельной работы.
Воспитательные:
воспитание дисциплинированности при организации работы на уроке;
воспитание аккуратности при выполнении построений.
Структура урока:
Проверка домашнего задания.
Актуализация опорных знаний.
Диагностика усвоения знаний и умений учащихся.
Подведение итогов урока.
1. Организационный момент
2. Проверка домашнего задания
- А сейчас проверим, как вы выполнили домашнее задание. По заданным координатам вы должны были построить фигуру, соединяя, по мере построения, соседние точки друг с другом. В результате выполнения работы у вас должна была получиться фигура:

3. Актуализация опорных знаний
1. Две координатные прямые образуют координатную … (плоскость)
2. Координатные прямые - это координатные … (оси)
3. Какой угол образуется при пересечении координатных прямых? (прямой)
4. Как называется пара чисел, определяющих положение точки на плоскости? (координата)
5. Как называется первая координата? (абсцисса)
6. Как называется вторая координата? (ордината)
7. Как называется отрезок от 0 до 1? (единичный)
8. На сколько частей делится координатная плоскость координатными прямыми? (четыре)

4. Диагностика усвоения знаний и умений учащихся
На координатной плоскости отметьте точки:
А(-3; 0); В(2; -3); С(-4; 2); D(0; 4); E(1; 3); О(0; 0)

А теперь перейдем к построению фигуры с помощью точек на координатной плоскости. Даны координаты точек. Построить фигуру, соединяя, по мере построения, соседние точки друг с другом.
Читайте также:

