Вписанные и описанные треугольники конспект

Обновлено: 07.07.2024

Цели урока: научить учащихся анализировать теоретические знания, методы и приёмы с точки зрения их применимости к данной в задаче ситуации, прививать интерес к предмету, развивать мышление учащихся.

Организационный момент: учитель сообщает учащимся цели и задачи урока.

I. Учащимся предлагается отыскать основные способы вычисления радиуса вписанной окружности при решении следующей задачи:

В равнобедренном треугольнике основание равно 16 см, боковая сторона – 10 см. вычислите радиусы вписанной и описанной окружностей треугольника.

Учащиеся могут найти три способа:

1. использовать свойство радиуса окружности, проведенного в точку касания, и подобие треугольников,
2. применить формулу
3. учесть, что центр вписанной окружности – точка пересечения биссектрис, и использовать свойство биссектрисы треугольника.

После отыскания способов решения, учащимся предлагается решить задачу одним из способов, обязательно устанавливается, что все три способа выбраны для решения. На решение задачи отводится 10 минут. Далее все три способа решения записываются на доске.

Решение задачи: В

Дано: ∆ АВС, АВ = ВС = 10, К

Решение: опустим высоту ВМ на основание треугольника, АО – биссектриса ∠ ВАС, О – центр вписанной окружности, КО = ОМ = r.

1) ∆ ВОК ∞ ∆ ВАМ по двум углам ( ∠ В – общий, ∠ КОВ = ∠ МАВ = )

2) ∆ АВМ: , АВ = 10, АМ = 8, ВМ =

3) , 48 – 8r = 10r, 18r = 48, r =

1) Найдем площадь треугольника АВС по формуле Герона, либо по формуле S =

Используем свойство биссектрисы: биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные двум другим сторонам. Имеем: ,

Далее проводится точно такая же работа по отысканию способов вычисления радиуса описанной окружности. Устанавливается, что радиус описанной окружности можно найти следующими способами:

1. из подобия треугольников;
2. по свойству отрезков хорд окружности, проходящих через одну точку;
3. учитывая, что центр описанной окружности равноудалён от всех вершин треугольника;
4. по формуле

Дано: ∆ АВС, АВ = ВС = 10,

1) О – центр описанной окружности, ОК ⊥ АВ,

тогда АК=КВ=5 А С

2) ∆ АВМ ∞ ∆ ОВК по двум углам ( ∠ В – общий,

Используем данные, полученные при решении задачи о вписанной окружности:

1) Используем свойство пересекающихся хорд:

2) АМ = МС = АС : 2 = 8

3) ВМ = 6, МД = 2R – ВМ =2R – 6

4) 8 ∙ 8 = 6 ∙ (2R – 6), 2R – 6 = , 2R = , Д

1) О – центр окружности, точка О равноудалена от всех

вершин ∆ АВС, т.е. ∆ АОВ – равнобедренный.

2) Пусть МО = х, тогда ВО = АО = 6 + х А С

3) ∆ АМО – прямоугольный, АМ = 8, АО = 6 + х.

(х+6-х) ∙ (х+6+х) = 64, х = , R = х + 6 =

Найдём площадь ∆ АВС и используем формулу

III. Домашнее задание:

1. ОГЭ 3000 задач: № 2148, 2146, 2156, решить задачу несколькими способами.
2. П.77-78, вписанная и описанная окружности.

По теме: методические разработки, презентации и конспекты

Конспект урока "Применение подобия треугольников для решения практических задач"

Урок повторения и обобщения знаний по теме: "Подобие треугольников". В ходе урока учащиеся расширяют знания о признаках подобия треугольников, определяют области применение подобия треугольников.

Конспект урока "Решение практических задач по теме "Треугольники""

Урок систематизации и обобщения материала по теме "Треугольники", направленный на повторение, подготовке к экзамену и умению решать задачи с практическим содержанием.

Открытый урок: "Применение подобия треугольников при решении практических задач"

Технологическая карта урока "Решение практических задач по теме "Длина окружности.Площадь круга""

Описывает возможное проведение урока по данной теме.

Тест по теме "Вписанная и описанная окружности треугольника" по геометрии 7 класс к учебнику Мерзляк А. Г.

Презентация к уроку геометрии в 8 классе "Описанная и вписанная окружности четырёхугольника"

Презентация к уроку геометрии в 8 классе "Описанная и вписанная окружности четырёхугольника".

Технологическая карта урока-исследования в 7 классе на тему: Применение признаков равенства треугольников к решению практических задач.

Тип урока: урок-исследование.Форма работы учащихся: фронтальная, групповая, индивидуальная.Виды деятельности: работа с текстом, решение практических задач на производстве, в технике, в науке.Использов.

Описанные и вписанные окружности

Наглядная геометрия 9 класс. Опорный конспект 2 Описанные и вписанные окружности

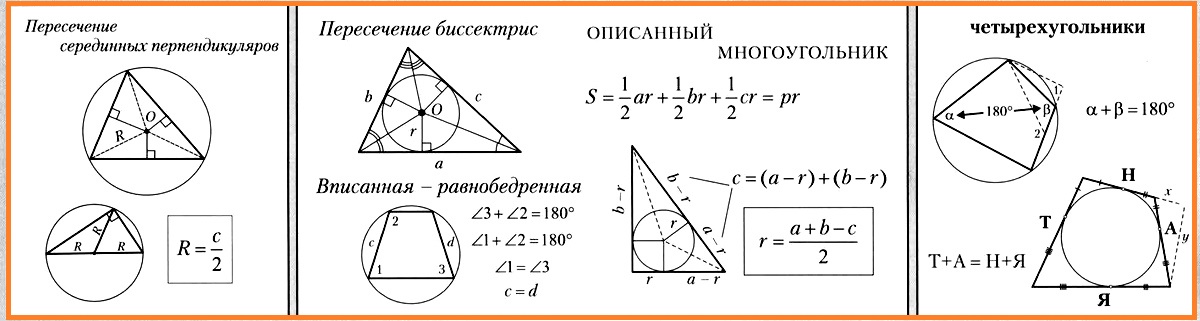
Около любого треугольника можно описать окружность. Она проходит через все вершины треугольника. Вы уже знаете, что точка пересечения серединных перпендикуляров равноудалена от вершин треугольника. Она и является центром описанной окружности.

В любой треугольник можно вписать окружность. Она касается всех сторон треугольника. Вы также знаете, что точка пересечения биссектрис треугольника равноудалена от сторон треугольника. Она и является центром вписанной окружности.

А можно ли описать окружность около любого параллелограмма? Если попробовать это сделать, то окажется, что около параллелограмма можно описать окружность, только если он — прямоугольник. Мы узнаем, каким свойством обладают вписанные и описанные четырехугольники и какие признаки позволяют судить о том, можно ли около данного четырехугольника описать и можно ли в него вписать окружность.

И вдобавок мы познакомимся с одной важной формулой площади треугольника S = рr.

1. Окружность, описанная около треугольника.

Окружность называется описанной около треугольника, если она проходит через все его вершины.

Теорема. Вокруг любого треугольника можно описать окружность, и только одну. Ее центр лежит на пересечении серединных перпендикуляров к сторонам треугольника.

Доказательство. Точка пересечения серединных перпендикуляров к сторонам треугольника равноудалена от его вершин (доказано нами в 7 классе). Поэтому она является центром описанной окружности, расстояние от этой точки до любой из вершин равно радиусу.

Если существует еще одна описанная окружность, то ее центр равноудален от всех трех вершин и поэтому совпадает с точкой пересечения серединных перпендикуляров, а радиус совпадает с радиусом первой окружности. Окружности совпадают.

2. Окружность, описанная около прямоугольного треугольника.

Теорема. Центр окружности, описанной около прямоугольного треугольника, лежит на середине гипотенузы, а радиус окружности равен половине гипотенузы.

Доказательство. Мы знаем, что медиана прямоугольного треугольника, проведенная из вершины прямого угла, равна половине гипотенузы (доказано нами в 7 классе). Поэтому середина гипотенузы является центром описанной окружности, а ее радиус равен половине гипотенузы, т. е. R = c/2.

3. Окружность, вписанная в треугольник.

Окружность называется вписанной в треугольник, ест она касается всех сторон треугольника.

Теорема. В любой треугольник можно вписать окружность, и только одну. Ее центр лежит на пересечении биссектрис треугольника.

Доказательство. Точка пересечения биссектрис треугольника равноудалена от сторон треугольника (доказано нами в 7 классе). Если из этой точки опустить перпендикуляры на стороны и провести окружность радиусом, равным перпендикуляру, то стороны треугольника будут касаться окружности по признаку касательной.

Если существует еще одна вписанная окружность, то ее центр равноудален от всех трех сторон и поэтому совпадает с точкой пересечения биссектрис, а радиус совпадает с радиусом первой окружности. Окружности совпадают.

4. Формула площади S = рr.

Теорема. Площадь треугольника S = рr, где р — полупериметр треугольника, r — радиус вписанной окружности.

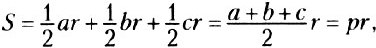
Доказательство. Соединим центр вписанной окружности с вершинами треугольника, стороны которого равны а, b и с. Получим три треугольника, для которых радиусы вписанной окружности, проведенные в точки касания, являются высотами. Площадь данного треугольника равна сумме площадей этих треугольников:

где p — полупериметр треугольника.

Данная формула справедлива для любого многоугольника, в который можно вписать окружность, т. е. для любого описанного многоугольника. Доказательство аналогично.

5. Окружность, вписанная в прямоугольный треугольник.

Теорема. Радиус окружности, вписанной в прямоугольный треугольник, находится по формуле r = (а + b – c)/2.

Доказательство. Проведем радиусы в точки касания. Получим квадрат со стороной r (четырехугольник, у которого все углы прямые и две соседние стороны равны по r) и отрезки катетов, равные r и а – r для катета а, r и b – r для катета b. Так как отрезки касательных, проведенных из одной точки, к окружности равны, то гипотенуза равна сумме отрезков (a – r) и (b – r). Так как с = (а – r) + (b – r), то r = (а + b – c)/2.

6. Свойство вписанного четырехугольника.

Теорема (свойство вписанного четырехугольника). Если четырехугольник вписан в окружность, то суммы его противоположных углов равны по 180°.

Доказательство. Противоположные углы α и β являются вписанными. Они опираются на дуги, которые дополняют друг друга до окружности. Окружность содержит 360°. Так как вписанный угол равен половине дуги, на которую он опирается, то сумма углов α и β равна 180°.

7. Признак вписанного четырехугольника.

Теорема (признак вписанного четырехугольника). Если сумма противоположных углов четырехугольника равна 180°, то вокруг него можно описать окружность.

Доказательство. Через три вершины четырехугольника всегда можно провести окружность (это вершины некоторого треугольника). Если четвертая вершина будет лежать внутри окружности или вне ее, то угол при этой вершине будет больше или меньше угла β, по свойству внешнего угла треугольника, т. е. 1 8. Свойство вписанной трапеции.

Теорема. Вписанная трапеция является равнобедренной.

Доказательство. 1-й способ. ∠1 + ∠2 = 180° как внутренние односторонние при параллельных прямых и секущей, ∠3 + ∠2 = 180° по свойству вписанного четырехугольника. Тогда ∠1 = ∠3 и трапеция равнобедренная по признаку равнобедренной трапеции.

2-й способ. Параллельные прямые отсекают равные дуги. Равные дуги стягиваются равными хордами. Поэтому боковые стороны трапеции равны.

9. Свойство описанного четырехугольника.

Теорема (свойство описанного четырехугольника). Если в четырехугольник можно вписать окружность, то суммы его противоположных сторон равны.

Доказательство. Отрезки касательных, проведенных из одной точки к окружности, равны. Обозначим равные отрезки соответственно одной черточкой, двумя, тремя и четырьмя. Убеждаемся, что суммы противоположных сторон равны: Т + А = Н + Я.

10. Признак описанного четырехугольника.

Теорема (признак описанного четырехугольника). Если у четырехугольника суммы противоположных сторон равны, то в него можно вписать окружность.

Доказательство. Пусть окружность касается только трех сторон. Повернув четвертую сторону вокруг вершины так, чтобы она касалась окружности, получим описанный четырехугольник.

Т + А = Н + Я — по свойству описанного четырехугольника,
Т + y = (Н + х) + Я — по условию.

Тогда y = А + х. А это противоречит неравенству треугольника у ЭТО НУЖНО ЗНАТЬ !

Вписанный треугольник — треугольник, все вершины которого лежат на окружности. Тогда окружность называется описанной вокруг треугольника.

Очевидно, расстояние от центра описанной окружности до каждой из вершин треугольника одинаково и равно радиусу этой окружности.

Вокруг любого треугольника можно описать окружность, причем только одну.

Окружность вписана в треугольник, если она касается всех его сторон. Тогда сам треугольник будет описанным вокруг окружности. Расстояние от центра вписанной окружности до каждой из сторон треугольника равно радиусу этой окружности.

В любой треугольник можно вписать окружность, причем только одну.

Попробуйте сами описать окружность вокруг треугольника и вписать окружность в треугольник.

Как вы думаете, почему центр вписанной окружности — это точка пересечения биссектрис треугольника, а центр описанной окружности — точка пересечения серединных перпендикуляров к его сторонам?

В задачах ЕГЭ чаще всего встречаются вписанные и описанные правильные треугольники.

Есть и другие задачи. Для их решения вам понадобятся еще две формулы площади треугольника, а также теорема синусов.

Вот еще две формулы для площади.
Площадь треугольника равна половине произведения его периметра на радиус вписанной окружности.

— радиус окружности, вписанной в треугольник.

Есть и еще одна формула, применяемая в основном в задачах части :

где — стороны треугольника, — радиус описанной окружности.

Для любого треугольника верна теорема синусов:

Ты нашел то, что искал? Поделись с друзьями!

. Радиус окружности, вписанной в равнобедренный прямоугольный треугольник, равен . Найдите гипотенузу c этого треугольника. В ответе укажите .

Треугольник прямоугольный и равнобедренный. Значит, его катеты одинаковы. Пусть каждый катет равен . Тогда гипотенуза равна .

Запишем площадь треугольника АВС двумя способами:

Приравняв эти выражения, получим, что . Поскольку , получаем, что . Тогда .

В ответ запишем .

. Сторона АС треугольника АВС с тупым углом В равна радиусу описанной около него окружности. Найдите угол В. Ответ дайте в градусах.

По теореме синусов,

Получаем, что . Угол — тупой. Значит, он равен .

. Боковые стороны равнобедренного треугольника равны , основание равно . Найдите радиус описанной окружности этого треугольника.

Углы треугольника не даны. Что ж, выразим его площадь двумя разными способами.

, где — высота треугольника. Ее найти несложно — ведь в равнобедренном треугольнике высота является также и медианой, то есть делит сторону пополам. По теореме Пифагора найдем . Тогда .

Задачи на вписанные и описанные треугольники особенно необходимы тем, кто нацелен на решения задания .

Например, на рисунке 8.106 .

Так, окружность можно вписать в квадрат и в ромб, но нельзя вписать в параллелограмм и в прямоугольник.

.

Так, окружность можно описать около квадрата и прямоугольника, но нельзя описать около параллелограмма и ромба.

а) в равностороннем треугольнике центром окружности является точка пересечения высот, биссектрис, медиан треугольника (центры вписанной и описанной окружностей совпадают (рис. 8.108);

б) в равнобедренном треугольнике центр окружности расположен на биссектрисе, проведенной из вершины треугольника к его основанию (рис. 8.109);

3) если треугольник прямоугольный, то центр окружности расположен на середине гипотенузы (рис. 8.110);

3) в равностороннем треугольнике центром окружности является точка пересечения высот, биссектрис, медиан треугольника.

Радиус окружности, описанной около многоугольника, как правило, обозначают , а радиус окружности, вписанной в многоугольник, обозначают :

1) для равностороннего треугольника со стороной :

, (8.34)

; (8.35)

2) для произвольного треугольника со сторонами и площадью :

; (8.37)

3) для прямоугольного треугольника с катетами и гипотенузой :

, (8.38)

4) для квадрата со стороной и диагональю :

, (8.40)

; (8.41)

5) для прямоугольника с диагональю :

; (8.42)

6) для ромба с высотой :

; (8.43)

7) для трапеции с высотой , при условии, что в трапецию можно вписать окружность:

. (8.44)

Если около трапеции можно описать окружность, то, проведя диагональ трапеции и рассмотрев один из полученных треугольников со сторонами и площадью , по формуле " height="" />
найдем радиус окружности описанной около треугольника, а значит и около трапеции (рис. 8.116);

8) для правильного шестиугольника со стороной :

, (8.45)

Правильный шестиугольник состоит из шести правильных треугольников (рис. 8.117) и точка является центром вписанной в него и описанной около него окружностей.

Пример 1. Найдите сторону квадрата, если известно, что разность между площадью квадрата и площадью вписанного в него круга равна .

Решение. Так как площадь круга радиуса находят по формуле 8.32 , а площадь квадрата со стороной находят по формуле " height="" />
, то согласно условию задачи запишем: -S_=12" height="" />
, -a^=2\pi -8" height="" />
.

.

Пример 2. Площадь прямоугольника равна 4, а разность длин его смежных сторон рана 3. Найдите радиус окружности, описанной около этого прямоугольника.

Решение. Площадь прямоугольника со смежными сторонами и находят по формуле .

Пусть , тогда (рис. 8.118).

Получим: , +3x-4=0" />
, откуда , следовательно, , .

По теореме Пифагора найдем диагональ прямоугольника: =1+16=17" />
, " />
. Согласно формуле 8.42 " />
.

.

=\left (\frac> \right )^+\left ( \frac \right )^" />
, =3^+4^" />
, .

По формуле d_d_" />
найдем площадь ромба: \cdot 6\cdot 8=24" />
.

Но площадь ромба можно найти и по формуле , а так как , то . Тогда , а .

.

Решение. Площадь правильного треугольника со стороной находят по формуле: a^>" />
.

Зная площадь треугольника, найдем его сторону: a^>=4\sqrt" />
, =16" />
, .

.

.

.

Пример 5. Радиус окружности, описанной около равнобедренного прямоугольного треугольника равен 2. Найдите радиус окружности, вписанной в этот треугольник.

Решение. Радиус окружности, описанной около прямоугольного треугольника с гипотенузой находят по формуле 8.38 . Тогда .

Так как треугольник равнобедренный, то его катеты и раны и по теореме Пифагора =2a^" height="" />
, откуда <\sqrt>" height="" />
, <\sqrt>=2\sqrt" height="" />
.

Радиус окружности, вписанной в прямоугольный треугольник, находят по формуле 8.39. В нашем случае " />
, -4>=2\sqrt-2" />
.

.

Пример 6. Один из катетов прямоугольного треугольника равен 8, а радиус окружности, вписанной в треугольник равен 3. Найдите площадь треугольника.

Решение. Рассмотрим прямоугольный треугольник . Точка является центром вписанной в треугольник окружности (рис. 8.120).

Так как радиусы вписанной в треугольник окружности перпендикулярны сторонам треугольника в точках касания, то имеем квадрат со стороной 3. Если катет , а сторона квадрата , то .

Пусть отрезок . По свойству касательных и .

Тогда по теореме Пифагора =AC^+AB^" height="" />
или =64+9+6x+x^" height="" />
, откуда , .

Найдем катет : .

Найдем площадь треугольника: =\frac\cdot AC\cdot AB" />
, =\frac\cdot 8\cdot 15=60" />
.

Пример 7. Окружность, центр которой расположен на большей стороне треугольника, делит эту сторону на отрезки 4 и 8 и касается двух других его сторон, длина одной из которых равна 6. Найдите радиус окружности, вписанной в этот треугольник (рис.8.121).

Решение. Согласно свойству биссектрисы треугольника запишем: =\frac" />
, откуда .

В свою очередь по формуле Герона " />
найдем площадь треугольника. Так как , то =9\sqrt" />
.

.

.

Пример 8. В прямоугольную трапецию вписана окружность радиуса 3, которая в точке касания делит ее боковую сторону на отрезки 4 и 5. Найдите площадь трапеции.

Решение. Согласно условию задачи и рисунку 8.122, запишем: , .

По свойству четырехугольника, описанного около окружности, получим: , , .

Согласно формуле (a+b)h" />
найдем площадь трапеции: \cdot 15\cdot 6=45" />
.

Пример 9. Длины оснований равнобедренной трапеции относятся как , а длина ее высоты равна 17. Вычислите площадь круга, описанного около трапеции, если известно, что средняя линия трапеции равна ее высоте.

Решение. Рассмотрим равнобедренную трапецию (рис. 8.123) и проведем диагональ трапеции .

Радиус окружности, описанной около треугольника , найдем по формуле 8.36 :

>=\frac\cdot AD\cdot BN>" />
, " />
.

Зная, что и вводя коэффициент пропорциональности , получим , .

Так как длина средней линии трапеции равна высоте трапеции, то (5k +12k)=17" />
, откуда . Тогда , .

Поскольку четырехугольник является прямоугольником, то , тогда (24-10)=7" height="" />
.

+ND^>" />
, +17^>=17\sqrt" />
.

По формуле 8.36 найдем радиус окружности, описанной около треугольника , а, следовательно, и около трапеции :

.

Согласно формуле 8.32 найдем площадь круга: .

Ответ: .

.

.

По формуле 8.46 найдем радиус окружности, вписанной в этот шестиугольник. Так как " />
, то " />
.

Площадь круга находят по формуле 8.32. Тогда =3\pi" />
, а =\frac<9\pi>" />
.

Найдем площадь кольца: =S_-S_" />
, =3\pi -\frac<9\pi >=\frac<3\pi >" />
.

Ответ: .

1. В любой треугольник можно вписать окружность и около любого треугольника можно описать окружность.

2. Не во всякий четырехугольник можно вписать окружность. Например, окружность можно вписать в ромб и квадрат, но нельзя вписать в параллелограмм и прямоугольник.

3. Не около всякого четырехугольника можно описать окружность. Например, окружность можно описать около квадрата и прямоугольника, но нельзя описать около параллелограмма и ромба.

4. Не во всякую трапецию можно писать окружность и не около всякой трапеции можно описать окружность. Описать окружность можно только около равнобедренной трапеции.

5. Если многоугольник правильный (все его стороны и все его углы равны между собой), то в него всегда можно вписать окружность и около него всегда можно описать окружность. Причем, центры этих окружностей совпадают.

Длину окружности радиуса находят по формуле:

. (8.30)

Площадь круга радиуса находят по формуле:

. (8.32)

Читайте также:

  
• Чтение рассказа житкова как я ловил человечков в старшей группе конспект
  
• Конспект игра драматизация курочка ряба
  
• Конспект урока по окружающему миру дыхание и кровообращение 3 класс
  
• Конспект урока по математике 3 класс самостоятельная работа 3 четверть
  
• Конспект дубровский 6 класс