Релейно контактные схемы конспект

Обновлено: 07.07.2024

Булевы функции широко применяются при описании работы дискретных управляющих систем (контактных схем, схем из функциональных элементов, логических сетей и т.д.), при исследовании некоторых электрических цепей, так называемых релейно-контактных схем.

Идея применения. Под релейно-контактной схемой понимается Устройство из проводников и двухпозиционных контактов. Оно может быть предназначено, например, для соединения (или разъединения) полюсов источника тока с некоторым потребителем. Контакты релейно-контактной схемы могут быть двух типов: замыкающие и размыкающие. Каждый контакт подключен к некоторому реле (переключателю). К одному реле может быть подключено несколько контактов — как замыкающих, так и размыкающих. Технически реле представляет собой катушку с металлическим сердечником (магнитопроводом), вблизи которого находится соответствующий контакт.

Когда через катушку пропускается электрический ток, металлический сердечник намагничивается и замыкает все находящиеся при нем замыкающие контакты. Одновременно все размыкающие контакты, относящиеся к данному реле, размыкаются. Поскольку замыкающие контакты при отсутствии в реле электрического тока разомкнуты, то они называются также нормально разомкнутыми. Аналогично, размыкающие контакты называются также нормально замкнутыми. При обесточивании обмоток реле (т.е. когда реле отключается) все замыкающие контакты снова размыкаются, а все размыкающие, замыкаются.

Каждому реле ставится в соответствие своя булева переменная или , или , которая принимает значение 1, когда реле срабатывает, и принимает значение 0 при отключении реле. На чертеже все замыкающие контакты, подключенные к реле . Это означает, что при срабатывании реле не проводят электрический ток и им сопоставляется значение 0. При отключенном реле замкнуты, т. е. в этот момент им сопоставляется (другими словами, переменная принимает) значение 1.

Всей релейно-контактной схеме тогда ставится в соответствие булева переменная , зависящая от булевых переменных , сопоставленным тем реле, которые участвуют в схеме. Если при данном наборе состояний реле (некоторые из этих реле находятся в рабочем состоянии под током, остальные отключены, т.е. "обесточены") вся релейно-контактная схема проводит электрический ток, то переменной ставится в соответствие (другими словами, переменная принимает) значение 1. Если же при этом наборе состояний реле схема не проводит электрический ток, то считаем, что переменная у принимает значение 0. Поскольку каждый набор состояний реле характеризуется набором, составленным из нулей и единиц и имеющим длину от , которые соответствуют тем состояниям реле , при которых данная схема проводит электрический ток. Такая булева функция называется функцией проводимости данной релейно-контактной схемы.

Таким образом, теория булевых функций предоставляет математические модели реальных физических релейно-контактных схем.

Рассмотрим некоторые релейно-контактные схемы и найдем их функции проводимости. Первая схема состоит из двух последовательно соединенных контактов , т. е. контактов, связанных с двумя независимыми реле , каждое из которых срабатывает независимо от другого:

Ясно, что данная схема проводит электрический ток тогда и только тогда, когда оба контакта замкнуты, т. е. только тогда, когда оба переменных принимают значение 1. Булева функция от двух аргументов , удовлетворяющая такому условию, нам хорошо известна. Это конъюнкция . Таким образом, функцией проводимости релейно-контактной схемы, состоящей из двух последовательно соединенных контактов , является конъюнкция . Говорят, что последовательное соединение двух контактов реализует конъюнкцию соответствующих этим контактам булевых переменных.

Вторая релейно-контактная схема состоит из двух параллельно соединенных контактов

Ясно, что эта схема проводит электрический ток в том и только в том случае, когда по меньшей мере один из контактов () замкнут, т.е. лишь в случае, когда хотя бы одна из булевых переменных () принимает значение 1. Булева функция от двух аргументов , удовлетворяющая этому условию, также хорошо нам известна. Это, дизъюнкция . Таким образом, функцией проводимости релейно-контактной схемы, состоящей из двух параллельно соединенных контактов , является дизъюнкция . Говорят, что параллельное соединение двух контактов реализует дизъюнкцию соответствующих этим контактам булевых переменных.

Итак, с помощью релейно-контактных схем можно реализовывать булевы функции: конъюнкцию, дизъюнкцию и отрицание. Возможна ли аналогичная реализация и других булевых функций? Ответ на поставленный вопрос позволяет дать теорема 10.5. Поскольку всякая булева функция на основании этой теоремы может быть выражена через конъюнкцию, дизъюнкцию и отрицание, причем отрицание стоит лишь непосредственно около переменных и не стоит ни около каких внутренних скобок, а конъюнкция, дизъюнкция и отрицание, как показано только что, реализуются на релейно-контактных схемах, то и всякая булева функция может быть реализована с помощью релейно-контактной схемы , т. е. может быть построена такая схема, для которой данная булева функция служит функцией проводимости.

Реализуем, например, в виде релейно-контактных схем булевы функции — импликацию и эквивалентность. Для этого выразим их через конъюнкцию, дизъюнкцию и отрицание. Такие выражения известны (см. теорему 9.5):

Предлагается самостоятельно нарисовать схему, реализующую функцию . Релейно-контактная схема, реализующая функцию , будет состоять из двух последовательно соединенных ветвей, первая из которых реализует булеву функцию , а вторая — булеву функцию . В свою очередь, первая из ветвей будет состоять из двух параллельных участков, один из которых содержит контакт , а второй — контакт . Аналогично, вторая ветвь также будет состоять из двух параллельных участков, один из которых содержит контакт . Изображаем полученную релейно-контактную схему (чтобы упростить рисунки, не будем изображать сами контакты, а ограничимся символом булевой переменной, соответствующей данному контакту):

Две основные задачи теории релейно-контактных схем

Составление релейно-контактных схем с заданными условиями работы называется задачей синтеза релейно-контактных схем и является первой важной задачей, состоящей в том, что требуется построить схему, которая проводила бы электрический ток лишь при вполне определенных задаваемых условиях.

Естественно было бы выбирать для каждой булевой функции самую простую или одну из самых простых реализующих ее релейно-контактных схем. Поэтому упрощение релейно-контактных схем называется задачей анализа таких схем и является второй важной задачей теории релейно-контактных схем. Две релейно-контактные схемы, составленные из одних и тех же реле, называются равносильными, если одна из них проводит ток тогда и только тогда, когда другая схема проводит ток. Другими словами, две схемы, составленные из одних и тех же реле, равносильны, если они обладают одинаковыми функциями проводимости, зависящими от одних и тех же переменных. Из двух равносильных схем более простой считается та, которая содержит меньшее число контактов. Задача упрощения релейно-контактной схемы состоит в нахождении более простой равносильной ей схемы. Обычно она решается следующим образом. Для данной релейно-контактной схемы записывается ее функция проводимости. Затем эта функция с помощью тождественных преобразований, использующих известные свойства булевых функций, упрощается, т.е. сводится к функции, имеющей меньшее число вхождений переменных, нежели исходная функция. Наконец строится релейно-контактная схема, отвечающая упрощенной булевой функции.

Автоматические устройства подразделяются на устройства дискретного и устройства непрерывного действия. К первому относятся, например, цифровые вычислительные машины. Работа устройств первого типа характеризуется прерывной, скачкообразной сменой конечного числа состояний. Примером устройств непрерывного действия являются моделирующие или аналоговые машины. Для них характерно непрерывное плавное изменение состояний. Физическая природа автоматических устройств определяется электротехническими, механическими и другими характеристиками элементов, которые их составляют. Кроме физических свойств, составляющие элементы имеют функциональные характеристики, которые учитывают назначение каждого элемента. Эти функциональные характеристики образуют логическую структуру устройства.

Логическим синтезом схемы дискретного действия называется определение логической структуры устройства по заданным условиям его работы. Логическим анализом схемы дискретного действия называется определение условий работы устройства по его известной логической структуре.

Оказалось, что имеется глубокое сходство между элементами такого типа и высказываниями. Это и послужило основой для применения алгебры высказываний к синтезу и анализу схем дискретного действия.

Впервые идея о возможности такого применения была высказана в 1910 г. голландским физиком Паулем Эренфестом.

2. Представление произвольной функции алгебры логики посредством параллельно-последовательной релейной контактной схемы.

В схемах применяются замыкающиеся и размыкающиеся контакты. Первые в рабочем состоянии замыкают, а в не рабочем размыкают ее. Вторые наоборот. Одинаковыми большими буквами мы будем обозначать контакты, замыкаемые или размыкаемые одним и тем же управляющим устройством (реле, выключателем и т. п.).

Применение алгебры высказываний к синтезу и анализу контактных
схем основано на возможности интерпретировать булеву алгебру в терминах электрических цепей.

Дизъюнкции AvB соответствует схема, составленная из двух параллельно-соединенных контактов А и В. Действительно, схема, состоящая из двух параллельно соединенных контактов, пропускает ток тогда и только тогда, когда замкнут хотя бы один из контактов.

Конъюнкции А&В соответствует схема, составленная из двух последовательно соединенных контакт А и В. Действительно, схема, состоящая из двух последовательно соединенных контактов, пропускает ток тогда и только тогда, когда замкнуты оба контакта.

Отрицанию высказывания А соответствует размыкающий контакт А, управляемый тем же устройством, что и контакт А.

Под переключаемой схемой понимают схематическое изображение некоторого устройства, состоящее из элементов:

1) переключателей, которые могут быть механическими устройствами, электромагнитное реле и т.д.;

2) соединяющих их проводников;

3) входов в схему и выходов из нее (клеммы, на которые подается электрическое напряжение). Они называются полюсами.

Через 1 обозначим такое состояние электрической цепи, при котором та проводит ток, через 0 – состояние, при котором она ток не проводит.

Рассмотрим зависимости между шинами соединения переключателей и состояниями цепи.

Ответ: A&B v C v D

3. Задачи на анализ и синтез релейно-контактных схем.

I. Упростить релейно-контактную схему и произвести ее анализ работы.

а) Для упрощения схемы записываем ее структурную формулу.
б) Затем полученную формулу упрощаем равносильным образом доминимального числа вхождения букв.
в) По полученной формуле восстанавливаем соответствующую ей схему. Эта схема работает также как первоначальная, но проще ее, т.к. содержит меньшее число контактов.

Первое преобразование правило поглощения для каждой скобки, второе – применение распределительного закона, третье – группируем первую и третью конъюнкции и применяем распределительный закон, четвертое – применяем закон исключения третьего (в скобках), а затем тавтологию тавтологии.

Строим для полученной формулы схему:

Анализ работы схемы можно произвести по первоначальной формуле, соответствующей этой схеме, но лучше работать с упрощенной формулой, т.к. это сопряжено с меньшими вычислениями. Для формулы составляется таблица истинности, которая показывает, при каких положениях контактов схема пропускает ток, а при каких нет.

Для учеников 1-11 классов и дошкольников
Бесплатные сертификаты учителям и участникам

Релейно-контактные схемы — это схемы выполненные с помощью электромагнитных или твердотельных реле. Рассмотрим их как логические устройства.

Для этих устройств характерно использование двух групп логических переменных отличающихся формой их представления.

Логические переменные представлены здесь:

1. Уровнем электрического напряжения подаваемого на катушку реле. Переменные этой группы истинны, если уровень напряжения достаточен для срабатывания реле (H-уровень) и ложны (L-уровень) если недостаточен.

2. Состоянием электрических цепей образованных либо отдельными контактами реле, либо двухполюсниками, полученными при соединении этих контактов. Переменные этой группы истинны, если соответствующие цепи замкнуты и ложны, если разомкнуты.

В конкретной релейно-контактной схеме переменные обеих групп обычно связаны друг с другом т.к. катушки реле управляют состоянием контактов, а контакты в свою очередь могут подавать напряжение на катушки. Логические переменные, действующие в релейно-контактных устройствах, будем обозначать на принципиальных схемах малыми латинскими буквами, заключенными в скобки. Так логические переменные описывающие работу реле К1 с замыкающим и размыкающим контактами следует обозначить на схеме следующим образом:

Легко видеть, что эти переменные связаны соотношениями

Таким образом, замыкающий контакт реле повторяет логическую переменную, поступающую на его катушку, а размыкающий контакт инвертирует эту переменную .

Рассмотрим далее двухполюсники X и Y образованные последовательным и параллельным соединением контактов реле К1 и К2. Построим для них таблицы истинности, считая, что входные логические переменные a и b представлены здесь состоянием этих контактов. Пусть схема двухполюсника имеет вид:

Очевидно, что цепь двухполюсника X замкнута (X=1), если одновременно будут замкнуты оба контакта И К1 И К2. Таблица истинности этого двухполюсника имеет вид:

Таблица истинности двухполюсника совпадает с таблицей истинности логического элемента И. Таким образом, последовательное соединение контактов в контактном двухполюснике реализует операцию логического умножения переменных представленных состоянием этих контактов .

Для двухполюсника Y имеем следующую принципиальную схему:

Очевидно, что цепь двухполюсника Y будет замкнута (Y=1), если будут замкнуты ИЛИ контакт К1 ИЛИ контакт К2 ИЛИ оба контакта одновременно. Таблица истинности двухполюсника имеет вид:

Таблица истинности этого двухполюсника совпадает с таблицей истинности логического элемента ИЛИ .

Таким образом, параллельное соединение контактов в контактном двухполюснике реализует операцию логического сложения переменных представленных состоянием этих контактов .

Рассмотренные правила позволяют вести анализ логических функций простейших релейно-контактных схем.

Остальные типы функций, реализуемых с помощью реле, основываются на придании контактной группе дополнительных свойств. Функции и типы контактов реле показаны на рисунке ниже.

1 — катушка реле (управляющая цепь), 2 — нормально открытый контакт, 3 — нормально закрытый контакт, 4 — нормально открытый контакт с замедлителем при срабатывании, 5 — нормально открытый контакт с замедлителем при возврате, 6 — нормально открытый контакт импульсный, 7 — нормально открытый контакт без самовозврата, 8 — нормально закрытый контакт без самовозврата, 9 — нормально закрытый контакт с замедлителем при срабатывании, 10 — нормально закрытый контакт с замедлителем при возврате.

Среди технических средств автоматизации значительное место занимают устройства релейно-контактного действия. Они широко используются в технике автоматического управления, в электронно-вычислительной технике и т.д.

Эти устройства (их в общем случае называют переключательными схемами) содержат сотни реле, электронных ламп, полупроводников и электромагнитных элементов. Описание и конструирование таких схем в силу их громоздкости весьма затруднительно.

Еще в 1910 году физик П. С. Эренфест указал на возможность применения аппарата алгебры логики при исследовании релейно-контактных схем (РКС). Однако его идеи стали реализовываться значительно позже, когда создание общей теории конструирования РКС стало остро необходимым.

Использование алгебры логики в конструировании РКС оказалось возможным в связи с тем, что каждой схеме можно поставить в соответствие некоторую формулу алгебры логики, и каждая формула алгебры логики реализуется с помощью некоторой схемы.

Это обстоятельство позволяет выявить возможности заданной схемы, изучая соответствующую формулу, а упрощение схемы свести к упрощению формулы.

С другой стороны, до построения схемы можно заранее описать с помощью формулы те функции, которые схема должна выполнять.

Рассмотрим, как устанавливается связь между формулами алгебры логики и переключательными схемами.

Под переключательной схемой понимают схематическое изображение некоторого устройства, состоящего из следующих элементов:

1) переключателей, которыми могут быть механические действующие устройства (выключатели, переключающие ключи, кнопочные устройства и т. д.), электромагнитные реле, электронные лампы, полупроводниковые элементы и т.п.;

2) соединяющих их проводников;

3) входовв схему и выходовиз нее (клемм, на которые подается электрическое напряжение). Они называются полюсами схемы.

Сопротивления, конденсаторы и т.д. на схемах не изображаются.

Если принять во внимание не смысл высказывания, а только его значение, то можно считать, что любому высказыванию может быть поставлена в соответствие переключательная схема 1.

Формулам, включающим основные логические операции, также могут быть поставлены в соответствие переключательные схемы.

Конъюнкция двух высказываний р и q будет представлена двухполюсной схемой с последовательным соединением двух переключателей Р и Q (схема 2) .

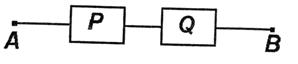
Эта схема пропускает ток тогда и только тогда, когда истинны и р, и q одновременно, то есть истинна конъюнкция р& q.

Дизъюнкция двух высказываний р и q изобразится двухполюсной схемой с параллельным соединением двух переключателей Р и Q (схема 3).

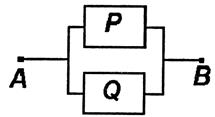
Эта схема пропускает ток в случае, если истинно высказывание р или истинно высказывание д, то есть истинна дизъюнкция p q .

Если высказывание р есть отрицание высказывания р, то тождественно истинная формула р p изображается схемой, которая проводит ток всегда (схема 4), а тождественно ложная формула р&р изобразится схемой, которая всегда разомкнута (схема 5).

Из схем 1, 2 и 3 путем последовательного и параллельного их соединения могут быть построены новые двухполюсные переключательные схемы, которые называют П-схемами.

Как было показано, всякая формула алгебры логики путем равносильных преобразований может быть представлена в виде формулы, содержащей только две операции: конъюнкцию и отрицание или дизъюнкцию и отрицание. Из этого следует, что всякая формула алгебры логики может быть изображена П-схемой и, обратно, для любой П-схемы может быть записана формула, которая изображается этой схемой.

Пример 1. Формуле соответствует схема 6:

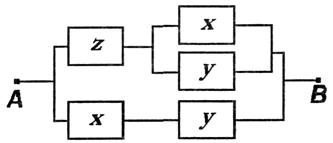
Пример 2. Для П-схемы 7

соответствующая формула алгебры логики имеет вид:

Упростим эту формулу следующим образом:

Последней формуле соответствует П-схема 8:

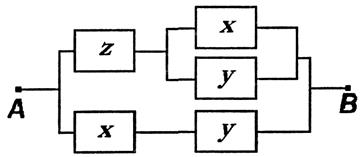
Из примера 2 следует, что для некоторых РКС путем равносильных преобразований соответствующей формулы алгебры логики можно получить РКС, содержащую меньшее число переключателей. Проблема решения этой задачи носит название проблемы минимизации.

Приведем пример построения РКС по заданным условиям с оценкой числа контактов.

Пример 3. Построить контактную схему для оценки результатов некоторого спортивного соревнования тремя судьями при следующих условиях: судья, засчитывающий результат, нажимает имеющуюся в его распоряжении кнопку, а судья, не засчитывающий результат, кнопки не нажимает. В случае, если кнопки нажали не менее двух судей, должна загореться лампочка (положительное решение судей принято простым большинством голосов).

Решение. Ясно, что работа нужной РКС описывается функцией Буля трех переменных F(x, у, z) , где переменные высказывания х, у, z означают:

Таблица истинности функции F(x, у, z) , очевидно, имеет вид:

F(x,y,z)

В связи с этим СКНФ формулы (функции) F(x,y,z) запишется в виде

А этой формуле соответствует РКС, изображенная на схеме 7, которая содержит двенадцать переключателей.

Но как было показано, в результате равносильных преобразований формула F(x, у, z) может быть приведена к виду:

которому соответствует РКС, изображенная на схеме 8, содержащей пять переключателей.

Читайте также: