Приращение функции конспект кратко

Обновлено: 06.07.2024

При изучении поведения функции y = f ( x ) около конкретной точки x 0 , необходимо знать, как меняется значение функции при изменении значения аргумента. Введём следующие понятия.

Пусть функция y = f ( x ) определена в точках x 0 и x 1 . Разность x 1 − x 0 называют приращением аргумента (при переходе от точки x 0 к точке x 1 ), а разность f ( x 1 ) − f ( x 0 ) называют приращением функции .

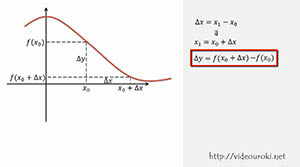
Итак, x 1 − x 0 = Δ x , значит, x 1 = x 0 + Δ x .

f ( x 1 ) − f ( x 0 ) = Δ y , значит, Δ y = f ( x 0 + Δ x ) − f ( x 0 ) .

Функция y = f ( x ) непрерывна в точке $x=a$, когда в этой точке выполняется условие: если Δ x → 0 , то Δ y → 0 ,

Урок на тему: "Приращение аргумента, приращение функции"

Что будем изучать:

1.Определение приращения аргумента, приращения функции.
2. Непрерывная функция и приращение.
3. Примеры.

Определение приращения аргумента и приращения функции

Ребята, мы с вами научились находить пределы функции в точке. Важным остается вопрос, как изменяется значение функции при изменении значения аргумента около этой точки?
Математики ввели такое понятие – приращение аргумента и функции. Давайте запишем определение.

Определение: Пусть функция $y=f(x)$ определена в точках $x_0$ и $x_1$. Разность $x_1-x_0$ называют приращением аргумента, а разность $f(x_1)-f(x_0)$–приращением функции.
Иначе говоря, узнаем прирост точки $x_0$ в точке $x_1$. Приращение аргумента обозначают как $Δx$, читается как дельта x.
Приращение функции обозначают, как $Δy$ или $Δf(x)$.
Из нашего определения следует: $x_1-x_0=Δx$ => $x_1= Δx+x_0$ и $f(x_1)-f(x_0)=Δy$. Тогда получаем важное равенство: $Δy=f(x_0+ Δx)-f(x_0)$. Приращение функции может быть как положительным, так и отрицательным.

Давайте рассмотрим пример.
Найти приращение функции $y=х^3$ при переходе от $x_0=2$ к точке:
а) $x=2,1$; б) $x=1,9$.

Решение:
Обозначим $f(x)=х^3$.
Имеем: $f(2)=2^3=8$.

а) Воспользуемся формулой $Δy=f(x_0+ Δx)-f(x_0)$.
Нам надо найти значение $f(2,1)$.
$f(2,1)=2,1^3=9,261$.
$Δy= f(2,1)- f(2)= 9,261-8=1,261$.
б) $f(2)=8$.
$f(1,9)=1,9^3=6,859$.
$Δy= f(1,9)- f(2)= 6,859-8=-1,141$.

Ответ: а) $1,261$; б) $-1,141$.

Непрерывная функция и приращение

Ребята, давайте вернемся к определению непрерывной функции, и посмотрим на него с помощью приращений.
Вспомним определение непрерывной функции.
Определение. Функцию $y=f(x)$ называют непрерывной в точке $x=a$, если выполняется тождество: \[\lim_f(x)=f(a)\] Обратим внимание: $x →a$, тогда $(x-a) →0$ т.е. $Δx → 0$.

Также заметим: $f(x) → f(a)$ , значит $f(x) - f (a) → 0$ т.е. $Δy → 0$.

Определение непрерывности функции в точке можно записать так.
Функция $y=f(x)$ непрерывна в точке $x=a$, если в этой точке выполняется следующее условие: если $Δx→0$, то $Δy → 0$.

Примеры

1. Для функции $y=kx+b$ найти:
а) приращение функции при переходе от фиксированной точки $x$ к $x+ Δx$;

б)предел отношения приращения функции к приращению аргумента при условии, что приращение аргумента стремится к нулю.

а) $f(x)= kx+b$.
$f(x+ Δx)=k(x+Δx)+b$;
$Δy= f(x+ Δx)-f(x)= k(x+Δx)+b-( kx+b)= kx+kΔx+b – kx-b= kΔx$.

2. Для функции $y=x^3$ найти:
а) приращение функции при переходе от фиксированной точки $x$ к $x+ Δx$.

а) $f(x)= x^3$.
$f(x+ Δx)=(x+Δx)^3=x^3+3x^2Δx+3xΔx^2+Δx^3$.
$Δy= f(x+Δx)-f(x)= x^3+3x^2Δx+3xΔx^2+Δx^3-x^3=3x^2Δx+3xΔx^2+Δx^3$.

Задачи для самостоятельного решения:

1) Найти приращение функции $y=x^4$ при переходе от $x_0=3$ к точке:
а) $x=3,2$;
б) $x=2,8$.

2) Для функции $y=3x+5$ найти приращение функции при переходе от фиксированной точки $x$ к $x+ Δx$.

3) Для функции $y=x^2$ найти приращение функции при переходе от фиксированной точки $x$ к $x+ Δx$.

4) Для функции $y=2x^3$ найти приращение функции при переходе от фиксированной точки $x$ к $x+ Δx$.

Для учеников 1-11 классов и дошкольников
Бесплатные сертификаты учителям и участникам

3.Правило нахождения производной.

I. Производная произведения.

II . Производная дроби.

4 .Производная сложной функции.

5 . Производная тригонометрических функций.

6 . Метод интервалов.(повторение)

7 . Признак возрастания( убывания) функции.

8.Критические точки функции, максимумы, минимумы.

9. Исследование функции с помощью производной..

10. Наибольшее и наименьшее значение функции..

11 . Уравнение касательной.

12. Производная в физике и технике.

Основное назначение данного пособия состоит в том, чтобы помочь студенту преодолеть трудности при решении практических работ по математике.

При самостоятельном решении задач многие студенты нуждаются в постоянных консультациях относительно приемов и методов их решения. Такие консультации студент может получить при изучении этого пособия.

Такая форма изложение позволяет студенту сначала познакомиться с приемами решения типовых задач и оформлением записи их решений, а затем приступить к выработке навыков при решении практических работ.

Производная и ее применение

Тема 1. Приращение функции

Пусть нам дана какая- то функция y = f ( x ).

Проведем произвольную кривую линию и будем считать, что это график нашей функции.

Возьмем на оси ОХ первоначальное значение аргумент обозначим его Хо. Найдем графически соответствующее ему значение функции y ₀ = f ( x ₀ ) .

Возьмем на оси ОХ новое значение аргумента, обозначим его x . Разность между новым значением аргумента x и первоначальным x ₀ – это и есть приращение аргумента ∆ x (дельта x ).

Определение . Разность между новым значением аргумента и первоначальным называются приращение аргумента

∆ х = х – х ₀ – приращение аргумента ( дельта икс равно икс минус икс нулевое).

Из этого равенства следует, что

Найдем графически значение функции в точке x , то есть в точке x ₀ + ∆ x .

Определение . Разность между новым значением функции и первоначальным называется приращением функции.

Записывается так: ∆ f = f ( x ₀ +∆ x ) – f ( x ₀ ).

f ( x ₀ + ∆ x ) – новое значение функции (эф от икс нулевое плюс дельта икс).

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.

Получите невероятные возможности

Конспект урока "Приращение аргумента, приращение функции"

· познакомиться с понятием непрерывной функции;

· познакомиться с понятием предел функции в точке;

· рассмотреть примеры использования данных понятий для решения задач.

Прежде чем приступить к изучению нового материала, давайте выполним упражнение.

Не всегда нам надо знать точные значения тех или иных параметров. Иногда нам достаточно знать, как они изменяются. Например, если мы в течение одного дня выйдем на улицу, то нам не важно, на сколько именно изменилась температура воздуха, а нам важно похолодало или потеплело. Или при движении автомобиля нам, не важно, знать точную скорость, а важно определить разгоняется автомобиль или тормозит.

Причём, если на улице потеплело, то изменения будут со знаком плюс и наоборот если похолодало, то изменения будут со знаком минус.

Если автомобиль разгоняется, то изменения будут со знаком плюс, если тормозит – то со знаком минус.

Для описания таких изменений было введено понятие приращение.

Определение.

Пусть функция y = f(x) определена в точках x₀ и x₁. Разность x₁ – x₀ называют приращением аргумента, а разность f(x₁) – f(x₀) называют приращением функции.

Приращение аргумента обозначают так:

Приращение функции обозначают так:

Давайте рассмотрим, что же такое приращение аргумента и функции на графике.

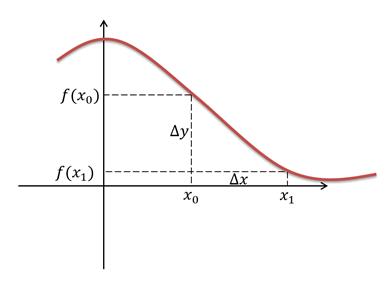
Рассмотрим ещё один пример.

Давайте вспомним определение непрерывной функции, которое мы формулировали ранее.

Определение непрерывности функции в точке x = a выглядит так:

Определение непрерывности функции в точке можно записать так:

Когда мы вводили определение непрерывной функции, то мы говорили, что функция непрерывна на промежутке X, если она непрерывна в каждой точке промежутка. Давайте уточним, что означает непрерывность функции в концевых точках промежутка, например, как понимать непрерывность функции в точках a и b отрезка [a; b].

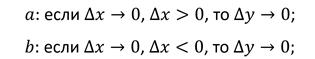
Давайте изобразим график линейной функции. Отметим приращение аргумента и функции. И найдём чему равно отношение приращения аргумента к приращению функции.

Читайте также: