Приближенное вычисление интегралов конспект

Обновлено: 07.07.2024

В тех случаях, когда при вычислении определенного интеграла невозможно найти первообразную или она очень сложна для вычислений, используют формулы приближенного вычисления.

Геометрический смысл определенного интеграла – площадь криволинейной трапеции, ограниченной осью кривой и прямыми Разобьем отрезок на равных частей точками Получим элементарных криволинейных трапеций.

Формулы прямоугольников.Площадь каждой элементарной трапеции можно приближенно вычислить как площадь прямоугольника.

Если построить прямоугольник, используя левую границу элементарной трапеции, получим формулу левых прямоугольников:

Очевидно, что чем больше тем точнее будет найдено значение интеграла.

Если построить прямоугольник, используя правую границу элементарной трапеции, получим формулу правых прямоугольников:

Для повышения точности вычисления можно построить прямоугольник, со стороной, равной значению подынтегральный функции в середине элементарного отрезка, получим формулу центральных прямоугольников:

На практике при вычислении определенного интеграла численными методами часто требуется обеспечить точность вычисления

Для оценки точности выполняют два расчета с числом разбиений и Вычисления заканчиваются, если при невыполнении неравенства число разбиений удваивается и вновь производится сравнение результатов.

Пример 1: Вычислить определенный интеграл используя формулы левых, правых и центральных прямоугольников. Обеспечить точность вычисления

Вводим отрезок интегрирования (рис. 28), (С2), (D2). Вычисляем значения подынтегральной функции на концах отрезка (B4, C4).

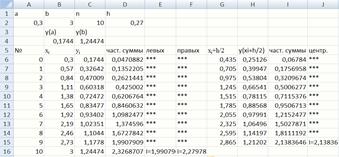
Рис. 28. Численное интегрирование по формулам прямоугольников

Заполнить блок А6:С16 самостоятельно.

Для заполнения ячейки D6используется формула =$D$2*C6. Для заполнения ячейки D7используется формула =$D$2*C7+D6, далее она протягивается вниз и заполняем весь столбец D.

Для заполнения ячейки Е6используется формула (рис. 29).

Для заполнения ячейки F6используется формула (рис. 30).

Рис. 29. Формула для заполнения ячейки Е6

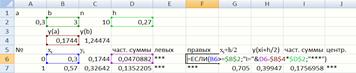
Рис. 30. Формула для заполнения ячейки F6

Далее они протягиваются вниз и заполняют столбцы EиF.

Заполнить блок G6:I15 самостоятельно.

Для заполнения ячейки J6используется формула (рис. 31).Далее она протягивается вниз и заполняет столбец J.

Рис. 31. Формула для заполнения ячейки J6

Выполняем вычисление определенного интеграла для

Оценку точности рассмотрим на примере формулы центральных прямоугольников.

Формула трапеций. Площадь каждой элементарной криволинейной трапеции можно приближенно вычислить как площадь трапеции, получим формулу трапеций:

Очевидно, что чем больше тем точнее будет найдено значение интеграла.

Пример 2: Вычислить определенный интеграл используя формулу трапеций. Обеспечить точность вычисления

Вводим отрезок интегрирования (рис. 32), (С2), (D2). Вычисляем значения подынтегральной функции на концах отрезка (B4, C4).

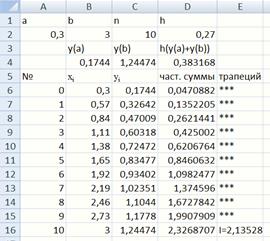
Рис. 32. Численное интегрирование по формуле трапеций

Заполнить ячейку D4 и блокА6:C16 самостоятельно.

Для заполнения ячейки Е6используется формула (рис. 33).Далее она протягивается вниз и заполняет весь столбец E.

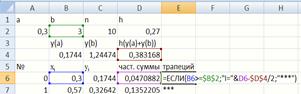
Рис. 33. Формула для заполнения ячейки E6

Выполняем вычисление определенного интеграла для

Формула Симпсона. Разобьем отрезок интегрирования на четное число элементарных отрезков точками

Подынтегральная функция на каждом элементарном отрезке двойной длины заменяется параболой. Значение интеграла приближенно вычисляется по формуле Симпсона:

Очевидно, что чем больше тем точнее будет найдено значение интеграла.

Пример3: Вычислить определенный интеграл используя формулу Симпсона. Обеспечить точность вычисления

Вводим отрезок интегрирования , (С2), заполняем ячейку D2(рис. 33). Вычисляем значения подынтегральной функции на конце отрезка (C4).

Рис. 33. Формула для заполнения ячейки E6

Заполнить блокА6:C16 самостоятельно.

Для заполнения ячейки D6используется формула =C6. Для заполнения ячейки D7используется формула =ЕСЛИ(ОСТАТ(A7;2)=0;D6+2*C7;D6+4*C7), далее она протягивается вниз и заполняем весь столбец D(рис. 34).

Для заполнения ячейки Е6используется формула (рис. 35).Далее она протягивается вниз и заполняет весь столбец E.

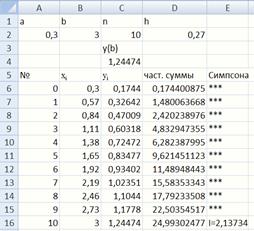
Рис. 34. Численное интегрирование по формуле Симпсона

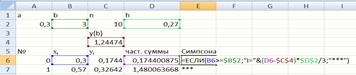
Рис. 35. Формула для заполнения ячейки E6

Выполняем вычисление определенного интеграла для

Задания для самостоятельного выполнения.

Из таблицы 5 приложения взять исходные данные своего варианта. Вариант определяется по порядковому номеру в списке группы. Выполнить численное интегрирование по формулам прямоугольников, трапеций и Симпсона. Обеспечить точность вычисления

Контрольные вопросы

1. Формулы прямоугольников.

2. Погрешность формул численного интегрирования

3. Формула трапеций.

4. Формула Симпсона.

Очевидно, что чем больше тем точнее будет найдено значение интеграла.

Рис. 28. Численное интегрирование по формулам прямоугольников

Заполнить блок А6:С16 самостоятельно.

Для заполнения ячейки Е6используется формула (рис. 29).

Для заполнения ячейки F6используется формула (рис. 30).

Рис. 29. Формула для заполнения ячейки Е6

Рис. 30. Формула для заполнения ячейки F6

Далее они протягиваются вниз и заполняют столбцы EиF.

Заполнить блок G6:I15 самостоятельно.

Для заполнения ячейки J6используется формула (рис. 31).Далее она протягивается вниз и заполняет столбец J.

Рис. 31. Формула для заполнения ячейки J6

Выполняем вычисление определенного интеграла для

Оценку точности рассмотрим на примере формулы центральных прямоугольников.

Очевидно, что чем больше тем точнее будет найдено значение интеграла.

Пример 2: Вычислить определенный интеграл используя формулу трапеций. Обеспечить точность вычисления

Рис. 32. Численное интегрирование по формуле трапеций

Заполнить ячейку D4 и блокА6:C16 самостоятельно.

Для заполнения ячейки Е6используется формула (рис. 33).Далее она протягивается вниз и заполняет весь столбец E.

Рис. 33. Формула для заполнения ячейки E6

Выполняем вычисление определенного интеграла для

Формула Симпсона. Разобьем отрезок интегрирования на четное число элементарных отрезков точками

Очевидно, что чем больше тем точнее будет найдено значение интеграла.

Пример3: Вычислить определенный интеграл используя формулу Симпсона. Обеспечить точность вычисления

Рис. 33. Формула для заполнения ячейки E6

Заполнить блокА6:C16 самостоятельно.

Для заполнения ячейки Е6используется формула (рис. 35).Далее она протягивается вниз и заполняет весь столбец E.

Рис. 34. Численное интегрирование по формуле Симпсона

Рис. 35. Формула для заполнения ячейки E6

Выполняем вычисление определенного интеграла для

Задания для самостоятельного выполнения.

Для учеников 1-11 классов и дошкольников
Бесплатные сертификаты учителям и участникам

ТЕМА: Приближенные методы вычисления определенных интегралов.

ЦЕЛЬ: рассмотреть приближенные методы вычисления интегралов на основании геометрического смысла интеграла.

образовательные:

- изучение приближенных методов вычисления определенных интегралов: метода прямоугольников и метода трапеций, параболических трапеций ;

- формирование умений и навыков вычисления определенных интегралов методами прямоугольников и трапеций, параболических трапеций ;

воспитательные :

– воспитание самостоятельности, инициативности, решительности, уверенности в себе, стремления к творческому поиску и исследовательской деятельности;

развивающие :

– развитие концентрации внимания, абстрактно-логического мышления,

ТИП: урок новых знаний.

МЕТОДЫ ОБУЧЕНИЯ: проблемное изложение учебного материала.

ВНУТРИДИСЦИПЛИНАРНЫЕ СВЯЗИ

Дифференциал функции и его приложение к приближенным вычислениям.

и определенный интегралы, методы их решений.

МЕЖДИСЦИПЛИНАРНЫЕ СВЯЗИ

Современные естественнонаучные знания о мире.

2.5. Вещество и поле, их взаимодействие.

Отражение результатов производства.

МАТЕРИАЛЬНОЕ ОБЕСПЕЧЕНИЕ: презентация, раздаточный материал.

Студент должен

знать:

формулы приближенного вычисления определенного интеграла:

- формулой параболических трапеций ( формула Симпсона) .

уметь:

- вычислять определенные интегралы приближенно методами прямоугольников и трапеций, параболических трапеций .

ХОД ЗАНЯТИЯ

1. Организационный момент

Решение многих технических задач сводится к вычислению определённых интегралов, точное выражение которых сложно, требует длительных вычислений и не всегда оправдано практически. Здесь бывает вполне достаточно их приближённого значения.

Очень часто приходится вычислять определённые интегралы, для которых невозможно найти первообразную. В этом случае применяют приближённые методы вычисления определённых интегралов. Иногда приближённый метод применяют и для “берущихся” интегралов, если вычисление по формуле Ньютона-Лейбница не рационально.

Преподаватель объявляет тему занятия, привлекает студентов к постановке целей и задач занятия.

3. Мотивация

Чтобы вдохновиться на изучение нового материала, вспомним о полезности интеграла.

Выясним, в чем состоит экономический смысл интеграла:

Экономический смысл интеграла

Z(t) — функция производительности труда от времени

V(t) — функция объема произведенной продукции от времени

V(t) — первообразная Z(t)

Объем произведенной продукции есть первообразная производительности труда

Применение интеграла в естествознании.

Перемещение за ограниченный интервал времени – это определенный интеграл скорости по времени:

Для нахождения работы необходимо найти определенный интеграл функции силы по перемещению:

4. Актуализация опорных знаний.

а) фронтальный опрос.

Что называют неопределенным интегралом функции ?

Что называют определенным интегралом от a до b функции ?

В чем состоит геометрический смысл определенного интеграла?

4) Какие два метода интегрирования вы знаете?

5) Какие вопросы можно задать об этих двух методах? (выбранный студент опрашивает группу о том, на чем основан метод непосредственного интегрирования и в каких случаях применяется метод замены переменной).

6) Что называют прямоугольником? Начертите изображение прямоугольника и запишите формулу его площади.

7) Выполните те же задания, но для трапеции.

б) тестирование по теме “Интеграл”.

Ответ : а) 27 б) 24 в) 18 г) 21

Ответ : а) -2 б) 2 в) -3 г) 3

Ответ : а) 26/3 б) 28/3 в) 15/2 г) 47/6

2) Найдите интеграл:

Ответ : а) 1.5 б) 2/3 в) -2/3 г) не существует.

3) При каком значении “а” выполняется равенство ?

Ответы : а) 2/3 б) 8/3 или -2 в) 2 или -1/3 г) -3

4) Вычислите площадь фигуры, ограниченной графиками функций: у=f(x), y=0, Y=-x 2 +x+2

Ответы : а) 13/3 б) 29/6 в) 16/3 г) 4,5

Ответы : а) 25/3 б) 28/3 в) 26/3 г) 29/3

Ответы : -3.5 б) 1.5 в) -1.5 г) -3.5

Ответ : а) 22/9 б) -14/9 в) -22/9 г) 14/9

2) Найдите интеграл.

Ответ : а) 0 б) -12 в) не существует. Г) 12

3) При каком значении “а” выполняется равенство ?

Ответы : а) 2, -13/3 б) -4 в) 4, -5/2 г) -3,9/4

Вычислите площадь фигуры, ограниченной графиками функций: у=f(x), y=0, Y=-x 2 +4x-3

Ответы : а) 4/3 б) -1,5 в) 11/6 г)7/6

5. Формирование новых знаний и способов действий

Организация деятельности

Предполагается, проводить работу 3-мя группами.

1-я группа – работает над формулой приближенного интегрирования — формулой прямоугольников

2-я группа – работает над формулой приближенного интегрирования – формулой трапеций

3-я группа – работает над формулой приближенного интегрирования – формулой параболических трапеций ( формула Симпсона)

Описание

Под непосредственным интегрированием понимают такой способ интегрирования, при котором данный интеграл путем тождественных преобразований подынтегральной функции и применения свойств неопределенного интеграла приводится к одному или нескольким табличным интегралам. Но вычислить интеграл непосредственным интегрированием удается далеко не всегда, а иногда это связано с большими трудностями. В этих случаях вычисление определенного интеграла по формуле Ньютона – Лейбница либо невозможно, либо затруднительно, поэтому прибегают к различным методам приближенного интегрирования.

Вычислить интеграл точно по формуле Ньютона – Лейбница с целью оценки погрешности при приближенном вычислении этого же интеграла.

Все три группы одновременно вычисляют интеграл :

Разделим интервал интегрирования на равных частей (частичных интервалов) и заменим данную трапецию ступенчатой фигурой, состоящей из прямоугольников, опирающихся на частичные интервалы, причем высоты этих прямоугольников равны значениям функции в начальных или конечных точках частичных интервалов. Значение площади этой фигуры и будет давать приближенное значение искомого интеграла .

Если обозначить значения функции в точках деления через , то будем иметь следующую формулу — формулу прямоугольников :

Оставим разбиение интервала прежним, но заменим теперь каждую дугу линии , соответствующую частичному интервалу . хордой, соединяющей конечные точки этой дуги. Таким образом, заменяем данную криволинейную трапецию прямолинейными. Площадь каждой трапеции, построенной на частичном интервале, равна полусумме площадей , соответствующих этому интервалу прямоугольников. Суммируя все эти площади, получим формулу трапеций :

Разобьем интервал на равных частей , но предположим, что – четное число: . Заменим дугу линии , соответствующую интервалу , дугой параболы, ось которой параллельна оси ординат и которая проходит через следующие три точки дуги: начальную точку дуги , среднюю точку , конечную точку . Площадь данной трапеции приближенно равна сумме площадей получающихся параболических трапеций и выражается формулой :

Решает пример 1 по формуле прямоугольников : при

Решает пример 1 по формуле трапеций : при

Решает пример 1 по формуле параболических трапеций : при

Занесем итоги расчета в таблицу и сравним:

Вывод : гипотеза о том, что с помощью формул численного интегрирования можно вычислять определенные интегралы подтвердилась. Однако, при одном и том же значении формула Симпсона дает лучшее приближение.

6. Закрепление материала

Пример 1. Вычислить по формуле прямоугольников . Найти абсолютную и относительную погрешности вычислений.

Разобьём отрезок [a, b] на несколько (например, на 6) равных частей. Тогда а = 0, b = 3 ,

х k = a + k х

х0 = 2 + 0* = 2 х1 = 2 + 1* = 2,5 х2 = 2 + 2* =3

х3 = 2 + 3 * = 3,5 х4 = 2 + 4* = 4 х5 = 2 + 5 * = 4,5

f (x 1 ) = 2 ,5 2 = 6,25

f (x 3 ) = 3,5 2 = 12,25

f (x 4 ) = 4 2 = 16

f (x 5 ) = 4,5 2 = 20,25

х 2 2,5 3 3,5 4 4,5

у 4 6,25 9 12,25 16 20,25

Для того, чтобы вычислить относительную погрешность вычислений, надо найти точное значение интеграла:

Пример 2 .Вычислить приближенно определенный интеграл по формуле трапеций. Результаты округлить до трёх знаков после запятой.

а) Разбив отрезок интегрирования на 3 части.
б) Разбив отрезок интегрирования на 5 частей.

Решение:
а)
По условию отрезок интегрирования нужно разделить на 3 части, то есть .
Вычислим длину каждого отрезка разбиения: . Параметр , напоминаю, также называют шагом.

Сколько будет точек (узлов разбиения)? Их будет на одну больше, чем количество отрезков:

Ну а общая формула трапеций сокращается до приятных размеров:

Для расчетов можно использовать обычный микрокалькулятор:

Обратите внимание, что, в соответствии с условием задачи, все вычисления следует округлять до 3-го знака после запятой.

б) Разобьём отрезок интегрирования на 5 равных частей, то есть . Увеличивая количество отрезков, мы увеличиваем точность вычислений.

Если , то формула трапеций принимает следующий вид:

Найдем шаг разбиения:
, то есть, длина каждого промежуточного отрезка равна 0,6.

При чистовом оформлении задачи все вычисления удобно оформлять расчетной таблицей:

Как формируется вторая строка– сначала записываем нижний предел интегрирования , остальные значения получаем, последовательно приплюсовывая шаг .

Если для 3 отрезков разбиения приближённое значение составило , то для 5 отрезков . Таким образом, с большой долей уверенности можно утверждать, что, по крайне мере .

Вычислить приближенно определенный интеграл по формуле Симпсона с точностью до 0,001. Разбиение начать с двух отрезков

Решение: Начинаем решать. Если у нас два отрезка разбиения , то узлов будет на один больше : . И формула Симпсона принимает весьма компактный вид:

Вычислим шаг разбиения:

Заполним расчетную таблицу:

Во второй строке сначала пишем нижний предел интегрирования , а затем последовательно приплюсовываем шаг .

В третью строку заносим значения подынтегральной функции. Например, если , то . Сколько оставлять знаков после запятой? Действительно, в условии опять об этом ничего не сказано. Принцип тот же, что и в методе трапеций, смотрим на требуемую точность: 0,001. И прибавляем дополнительно 2-3 разряда. То есть, округлять нужно до 5-6 знаков после запятой.

Первичный результат получен. Теперь удваиваем количество отрезков до четырёх: . Формула Симпсона для данного разбиения принимает следующий вид:

Вычислим шаг разбиения:

Заполним расчетную таблицу:

Таким образом:

Найдём абсолютное значение разности между приближениями:

Рассмотрим другое решение, где придётся сделать дополнительный шаг: так как больше требуемой точности: , то необходимо еще раз удвоить количество отрезков: .

Формула Симпсона растёт, как на дрожжах:

И снова заполним расчетную таблицу:

Погрешность меньше требуемой точности: . Осталось взять наиболее точное приближение , округлить его до трёх знаков после запятой и записать:

Ответ: с точностью до 0,001

Приведенные правила численного интегрирования помогают решать прикладные задачи.

Прикладная задача

Ширина реки равна 20м; промеры глубины в некотором поперечном ее сечении через каждые 2м дали следующую таблицу :

При решении физических и технических задач приходится находить определенные интегралы от функций, первообразные которых не выражаются через элементарные функции. Это привело к необходимости вывода приближенных формул вычисления определенных интегралов. Познакомимся с двумя из них: формулой трапеций и формулой парабол.

Время (минута)

Действия преподавателя

Действия обучающихся

Учебные материалы и ресурсы

Приветствовать обучающихся, отметить отсутствующих.

Проверить подготовленность обучающихся к учебному занятию.

Подготовится к учебному занятию.

Проверка выполнения домашнего задания

Ответы на вопросы по домашнему заданию (решение примеров)

Контроль усвоения материала.

Ответить на вопросы

Показать д-е задание.

Подготовка обучающихся к работе на основном этапе

Цели урока: Обучающая: вычисление площадей фигур; вычислять определенные интегралы и площади плоских фигур, проверка сформированности умений и навыков при решении примеров на их применение;

Развивающие: - содействовать развитию у учащихся мыслительных операций: умение анализировать, синтезировать, сравнивать;

Воспитывающая: воспитание дисциплины и норм поведения, творческого отношения к изучаемому предмету; стимулировать активность учащихся, повышать мотивацию к изучению математики. Тип урока: комбинированный, включающий освоение новых знаний.

Приближенное вычисление ОИ.

Формула трапеций.

Формула парабол.

Подготовить тетради и ручки.

Алгебра и начала математического анализа.

Формирование новых знаний и способов деятельности

Консультация Приближенное вычисление определенных интегралов

1. Формула трапеций.

Пусть требуется вычислить интеграл

, где f(x) - непрерывная функция. Для простоты рассуждений ограничимся случаем, когда f(x)³0. Разобьем отрезок [a, b] на n отрезков точками a=x₀ ₁ ₂ _k-1 _k _n =b и с помощью прямых х=х_k построим n прямолинейных трапеций (эти трапеции заштрихованы на рис. 1). Сумма площадей трапеций приближенно равна площади криволинейной трапеции, т.е.

Где f(x_k-1 ) и f(x_k ) - соответственно основания трапеций; x_k - x_k-1 = (b-a)/n - их высоты.

Таким образом, получена приближенная формула

которая и называется формулой трапеций. Эта формула тем точнее, чем больше n.

Рассмотрим в качестве примера интеграл

. Точное значение этого интеграла находится просто:

Вычислим теперь по формуле трапеций его приближенное значение. Пусть n=5. Тогда имеем: a=x₀ =0, x₁ =0,2, x₂ =0,4, x₃ =0,6, x₄ =0,8, x₅ =1=b и соответственно f(x₀ )=0, f(x₁)=0,04, f(x₂ )=0,16, f(x₃ )=0,36, f(x₄ )=0,64, f(x₅ )=1. Следовательно,

Точное значение интеграла равно 0,3333. поэтому абсолютная ошибка меньше 0,007. Во многих технических задач эта точность достаточна.

Если увеличить число n, то точность будет большей. Так, например, при n=10

т.е. абсолютная ошибка меньше 0,002.

В более полных курсах высшей математики доказывается, что если функция f(x) имеет на [a, b] непрерывную вторую производную, то абсолютная величина погрешности формулы трапеций не больше, чем

где k -наибольшее значение на отрезке [a, b].

Следует отметить, что с увеличением n увеличивается не только точность вычисления определенного интеграла, но и объем вычислительной работы. Однако здесь на помощь приходят ЭВМ.

Вычислим по формуле трапеции интеграл

при n=10. Разобьем отрезок [0, 1] на 10 равных частей точками х₀ =0, х₁ =0,1, . х₉ =0,9, х₁₀ =1. Вычислим приближенно значения функции f(x)=

в этих точках: f(0)=1,0000, f(0,1)=0.9091, f(0,2)=0,8333, f(0,3)=0.7692, f(0,4)=0,7143, f(0,5)=0,6667, f(0,6)=0,6250, f(0,7)=0,5882, f(0,8)= 0,5556, f(0,9)=0,5263, f(1)=0,5000.

По формуле трапеций получаем

Оценим погрешность полученного результата. Так как f(x)=1/(1+x), то

На отрезке [0, 1] имеем

. Поэтому погрешность полученного результата не превосходит величины

Вычислим точное значение данного интеграла по формуле Ньютона-Лейбница:

Абсолютная ошибка результата, полученного по формуле трапеций, меньше 0,0007. Это находится в соответствии с данной выше оценкой погрешности.

Идею, которая была использована при построении формулы трапеций, можно использовать для получения более точных приближенных формул для вычисления определенного интеграла

Внимательно слушать консультацию. Записывать важные информации.

Алгебра и начала математического анализа.

Первичная проверка понимания изученного материала

Составить диаграмму Венна на определенный и неопреленный интегралы.

Закрепление новых знаний и способов деятельности

2. Формула парабол. Докажем предварительно две леммы.

Лемма 1.1. Через любые три точки М₁(х₁ ; у₁ ), М₂(х₂ ; у₂ ), М₃(х₃ ; у₃ ) с различными абсциссами можно провести единственную кривую вида

Доказательство. Подставляя в уравнение параболы (1) координаты точек М₁ , М₂, М₃, получаем систему трех уравнений первой степени с тремя неизвестными А, В, С:

Так как числа х₁ , х₂ , х₃ различны, то определитель этой системы отличен от нуля:

Следовательно, данная система имеет единственное решение, т.е. коэффициенты А, В, С определяются однозначно. g

Отметим, что если А¹0, то кривая (1) является параболой, если А=0, то прямой.

Лемма 1.2. Площадь s криволинейной трапеции, ограниченной кривой у=Ах 2 +Вх+С, проходящей через точки М₁ (- h; y₁ ), M₂(0, y₂ ), M₃ (h, y₃ ) ( рис. 2) выражается формулой

(2)

Доказательство. Подставляя в уравнение у=Ах 2 +Вх+С координаты точек М₁ , М₂ , М₃ , получаем у₁ =А h 2 -В h +С ; у₂ =С ; у₃ =А h 2 +В h +С , откуда следует, что

2А h 2 +2С=у₁ +у₃ ; С=у₂(3)

Учитывая соотношение (3), имеем

Рассмотрим снова криволинейную трапецию, ограниченную произвольной кривой y=f(x). Разобьем отрезок [a, b] на 2p равных отрезков точками a=x₀ ₁ ₂_2k _2k+1 _2k+2 _2n-1_2n =b, а кривую y=f(x) с помощью прямых x=x_k на 2n соответствующих частей точками М₀ , М₁, М₂, . М₂ _k , М_2k+1 , М_2k+2, . М_2n-2 , М_2n-1 , М_2n(рис. 3).

Через каждую тройку точек

М₀ М₁М₂, . М₂ _k М_2k+1 М_2k+2 , . М_2n-2 М_2n-1 М_2n

проведем кривую вида у=Ах 2 +Вх +С (см. лемму 1.1). В результате получим n криволинейных трапеций, ограниченных сверху параболами или прямыми (эти трапеции заштрихованы на рис. 3). Так как площадь частичной криволинейной трапеции, соответствующей отрезку [x_2k , x_2k+2 ], приближенно равна площади соответствующей “параболической” трапеции, то по формуле (2) имеем [в данном случае h=(b-a)/(2n)]

Решить примеры вместе с преподавателем. Записывать важные информации.

Алгебра и начала математического анализа. 10-11 Алимов Москва 2014

Применение знаний и способов деятельности

Работа на доске.

Обобщение и систематизация знаний

Учим термины на английском языке. The Formula Newton – Leibniz

If the function is defined and continuous on the interval and is its integral (i.e. ), then Example. As one of the primitive then

Контроль и самоконтроль усвоения знаний и способов деятельности

Карточки с заданиями

Коррекция знаний и способов деятельности

Информация о домашнем задании

Записать домашнее задание

Алгебра и начала анализа

Подведение итогов занятия и рефлексия

На уроке происходит формирование умений и навыков вычисления определенных интегралов методами прямоугольников и трапеций с применением научного калькулятора.

Описание разработки

ЦЕЛИ УРОКА

- разработка приближенных методов вычисления определенных интегралов: метода прямоугольников и метода трапеций;

- формирование умений и навыков вычисления определенных интегралов методами прямоугольников и трапеций с применением научного калькулятора;

воспитательная – воспитание самостоятельности, инициативности, решительности, уверенности в себе, стремления к творческому поиску и исследовательской деятельности;

развивающая – развитие концентрации внимания, абстрактно - логического мышления, грамотной математической речи, творческих способностей;

методическая – использование проблемного изложения учебного материала.

ХОД УРОКА

1. Организационный момент

Приветствие, речь преподавателя:

Преподаватель объявляет тему урока (слайд №1), привлекает студентов к постановке целей урока.

3. Мотивация

Чтобы вдохновиться на изучение нового материала, вспомним о полезности интеграла.

Выясним, в чем состоит экономический смысл интеграла (слайд № 2). Рассмотрим две функции: f(t) – функцию производительности труда от времени и u(t) – функцию объема произведенной продукции от времени. Функция f есть производная функции u. Тогда скажите, чем является функция u для функции f? (студенты дают ответы). Итак, объем произведенной продукции есть первообразная производительности труда.

Применение интеграла в естествознании (преподаватель спрашивает студентов о применении интеграла в физике, так как это относится к теме предыдущего занятия). Теперь, вспомнив о практической значимости интеграла, перейдем к этапу воспроизведения знаний, необходимых нам для изучения новой темы.

4. Актуализация опорных знаний

Что называют неопределенным интегралом функции?
Что называют определенным интегралом от a до b функции?
В чем состоит геометрический смысл определенного интеграла?

4) Какие два метода интегрирования вы знаете?

6) Что называют прямоугольником? Создайте на интерактивной доске изображение прямоугольника и запишите формулу его площади (один студент создает изображение фигуры и записывает формулу на доске, в то время как другой в это время формулирует определение и теорему о площади).

7) Выполните те же задания, но для трапеции.

Теперь, собрав в голове все самые важные знания, мы готовы к изучению нового материала.

5. Изложение нового материала

5. 1. Преподаватель создает проблемную ситуацию, состоящую в нахождении интеграла (слайд № 3). Студенты делают вывод о том, что в этом случае не применимы изученные методы и признают ситуацию проблемной.

5. 2. Студенты формулируют учебную проблему урока и записывают ее в тетрадь (слайд № 4).

5. 3. Преподаватель ставит перед студентами проблемную задачу (слайд № 5, раздаточный материал), состоящую в приближенном вычислении площади территории страны, и предлагает высказать гипотезы. Студенты высказывают гипотезы и оформляют решения на интерактивной доске.

5. 4. Студентам предлагается вывести на основе предложенных гипотез новые формулы вычисления площади криволинейной трапеции (определенного интеграла). Студенты работают самостоятельно, а затем записывают свои рассуждения на интерактивной доске.

5. 5. Выведенные формулы (слайд № 6) студентами записываются в тетрадь. Делаются выводы о достоинствах и недостатках разработанных методов.

Мы разработали два новых метода вычисления интеграла. Теперь перейдем к этапу закрепления этих знаний при решении задач.

6. Закрепление материала

6. 2. Упражнение по обучению работе на научном калькуляторе (изучение функции 2 nd F).

6. 3. Решение задач на применение методов прямоугольников и трапеций к вычислению определенного интеграла (слайды № 9 - 10).

6. 4. Самостоятельная работа (слайд № 11).

7. Подведение итогов урока

Обобщаются новые знания, делаются выводы о достигнутых целях. Отмечаются активные студенты.

8. Домашнее задание

Студенты записывают домашнее задание (слайд № 12), преподаватель объясняет способ его выполнения.

Читайте также: