Площадь криволинейной трапеции и интеграл конспект

Обновлено: 20.05.2024

Ключевые слова: интеграл, криволинейная трапеция, площадь фигур, ограниченных лилиями

Оборудование: маркерная доска, компьютер, мультимедиа-проектор

Тип урока: урок-лекция

воспитательные: формировать культуру умственного труда, создавать для каждого ученика ситуацию успеха, формировать положительную мотивацию к учению; развивать умение говорить и слушать других.
развивающие: формирование самостоятельности мышления ученика по применению знаний в различных ситуациях, умения анализировать и делать выводы, развитие логики, развитие умения правильно ставить вопросы и находить на них ответы. Совершенствование формирования вычислительных, расчётных навыков, развитие мышления учащихся в ходе выполнения предложенных заданий, развитие алгоритмической культуры.
образовательные: сформировать понятия о криволинейной трапеции, об интеграле, овладеть навыками вычисления площадей плоских фигур

Метод обучения: объяснительно-иллюстративный.

В предыдущих классах мы научились вычислять площади фигур, границами которых являются ломаные. В математике существуют методы, позволяющие вычислять площади фигур, ограниченных кривыми. Такие фигуры называются криволинейными трапециями, и вычисляют их площадь с помощью первообразных.

Криволинейная трапеция (слайд 1)

Криволинейной трапецией называется фигура, ограниченная графиком функции , (щ.м.), прямыми x = a и x = b и осью абсцисс

Различные виды криволинейных трапеций (слайд 2)

Рассматриваем различные виды криволинейных трапеций и замечаем: одна из прямых вырождена в точку, роль ограничивающей функции играет прямая

Площадь криволинейной трапеции (слайд 3)

Зафиксируем левый конец промежутка а, а правый х будем менять, т. е., мы двигаем правую стенку криволинейной трапеции и получаем меняющуюся фигуру. Площадь переменной криволинейной трапеции, ограниченной графиком функции , является первообразной F для функции f

И на отрезке [a; b] площадь криволинейной трапеции, образованной функцией f, равна приращению первообразной этой функции:

Задание 1:

Найти площадь криволинейной трапеции, ограниченной графиком функции: f(x) = х 2 и прямыми у = 0, х = 1, х = 2.

Решение: (по алгоритму слайд 3)

Начертим график функции и прямые

Найдём одну из первообразных функции f(x) = х 2 :

Самопроверка по слайду

Интеграл

Рассмотрим криволинейную трапецию, заданную функцией f на отрезке [a; b]. Разобьём этот отрезок на несколько частей. Площадь всей трапеции разобьётся на сумму площадей более мелких криволинейных трапеций. (слайд 5). Каждую такую трапецию можно приближённо считать прямоугольником. Сумма площадей этих прямоугольников даёт приближённое представление о всей площади криволинейной трапеции. Чем мельче мы разобьём отрезок [a; b], тем точнее вычислим площадь.

Запишем эти рассуждения в виде формул.

Разделим отрезок [a; b] на n частей точками х₀ =а, х1,… ,хn = b. Длину k-го обозначим через хk = xk – xk-1. Составим сумму

Геометрически эта сумма представляет собой площадь фигуры, заштрихованной на рисунке (щ.м.)

Суммы вида называются интегральными суммами для функции f. (щ.м.)

Интегральные суммы дают приближённое значение площади. Точное значение получается при помощи предельного перехода. Представим, что мы измельчаем разбиение отрезка [a; b] так, что длины всех маленьких отрезков стремятся к нулю. Тогда площадь составленной фигуры будет приближаться к площади криволинейной трапеции. Можно сказать, что площадь криволинейной трапеции равна пределу интегральных сумм, Sк.т. (щ.м.) или интегралу, т. е.,

Интегралом функции f (х) от a до b называется предел интегральных сумм

Формула Ньютона- Лейбница.

Помним, что предел интегральных сумм равен площади криволинейной трапеции, значит можно записать:

Sк.т. = (щ.м.)

С другой стороны, площадь криволинейной трапеции вычисляется по формуле

S к. т. (щ.м.)

Сравнивая эти формулы, получим:

Это равенство называется формулой Ньютона- Лейбница.

Для удобства вычислений формулу записывают в виде:

1. Вычислить интеграл по формуле Ньютона- Лейбница: (проверяем по слайду 5)

2. Составить интегралы по чертежу (проверяем по слайду 6)

3. Найти площадь фигуры, ограниченной линиями: у = х 3 , у = 0, х = 1, х = 2. (Слайд 7)

Нахождение площадей плоских фигур (слайд 8)

Как найти площадь фигур, которые не являются криволинейными трапециями?

Пусть даны две функции, графики которых вы видите на слайде. (щ.м.) Необходимо найти площадь закрашенной фигуры. (щ.м.). Фигура, о которой идёт речь, является криволинейной трапецией? А как можно найти её площадь, пользуясь свойством аддитивности площади? Рассмотреть две криволинейные трапеции и из площади одной из них вычесть площадь другой (щ.м.)

Построить графики функций
Спроецировать точки пересечения графиков на ось абсцисс
Заштриховать фигуру, полученную при пересечении графиков
Найти криволинейные трапеции, пересечение или объединение которых есть данная фигура.
Вычислить площадь каждой из них
Найти разность или сумму площадей

Устное задание: Как получить площадь заштрихованной фигуры (рассказать при помощи анимации, слайд 8 и 9)

Домашнее задание: Проработать конспект, №353 (а), № 364 (а).

Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.

Дополнительная литература:

ОрловаЕ. А., СеврюковП. Ф., СидельниковВ. И., СмоляковА.Н.Тренировочные тестовые задания по алгебре и началам анализа для учащихся 10-х и 11-х классов: учебное пособие – М.: Илекса; Ставрополь: Сервисшкола, 2011.

Теоретический материал для самостоятельного изучения

Криволинейной трапецией называется фигура, ограниченная графиком непрерывной и не меняющей на отрезке [а;b] знака функции f(х), прямыми х=а, x=b и отрезком [а;b].

Отрезок [a;b] называют основанием этой криволинейной трапеции

формула Ньютона – Лейбница

Если в задаче требуется вычислить площадь криволинейной трапеции, то ответ всегда будет положительный. Если требуется, используя чертеж, вычислить интеграл, то его значение может быть любым(зависит от расположения криволинейной трапеции).

Примеры и разбор решения заданий тренировочного модуля

№1.Найти площадь криволинейной трапеции, изображенной на рисунке

Для вычисления площади криволинейной трапеции воспользуемся формулой Ньютона – Лейбница.

№2. Вычислить определенный интеграл:

Решение: Воспользуемся формулой Ньютона-Лейбница.

Сначала находим первообразную функцию F(x) . Далее подставляем значение верхнего предела в первообразную функцию: F(b) .

Затем подставляем значение нижнего предела в первообразную функцию: F(а).

Рассчитываем разность F(b) - F(а), это и будет ответ.

№3. Найти площадь криволинейной трапеции (х-1) 2 , ограниченной линиями х=2 и х=1, осью 0х

Воспользуемся формулой Ньютона-Лейбница.

Сначала находим первообразную функцию F(x). Далее подставляем значение верхнего предела в первообразную функцию: F(b) .

Затем подставляем значение нижнего предела в первообразную функцию: F(а).

цели урока: - ввести понятие криволинейной трапеции, сформулировать теорему о нахождении площади криволинейной трапеции, познакомить с понятием интеграла.

- формировать умения делать выводы.

-формировать интерес к изучению математики.

-развивать творческую активность учащихся.

§56 учебник алгебра и начала математического анализа Ш.А. Алимов и др.

материал вводится на наглядно-интуитивном уровне, поэтому использование презентации позволяет сделать объяснение более наглядным, а урок проходит интенсивнее.

Оборудование – компьютер, экран, проектор

Сформулировать тему и цели урока.

Учащиеся записывают в тетрадь тему урока

Изучение нового материала

Ввести понятие криволинейной трапеции

Рассмотрим фигуру изображенную на рисунке.

Рисунок и определение криволинейной трапеции в тетрадь

Работа с определением криволинейной трапеции

Рассмотрим виды криволинейной трапеции

Акцент на на рис 1

Каждый раз выделяя график функции, непрерывной и не меняющей знак на отрезке [a;b]

Затем точки с абсциссам х=а, х=в, еще раз выделяя особенности фигуры

Проверка усвоения понятия криволинейной трапеции

Поверка в форме устной работы

С последующей проверкой и разбором допущенных ошибок

Заполняют ответы в таблицу

Вместе с учителем

Работают с учителем и ведут записи в тетради

Работа с ведением понятия площади криволинейной трапеции

А можно ли найти площадь такой фигуры – криволинейной трапеции

Запись в тетрадь

Сначала рассмотрим интеграл как разность значений

Затем ввести его обозначение и чтение. Потом переход к записи формулы нахождения площади через интеграл

Дается краткая историческая справка о названии формулы и о ее авторах

Запись в тетрадь

Отработка алгоритма нахождения площади криволинейной трапеции

Рассмотрим на примере задачи 1 учебника

Работа ведется под руководством учителя.

Важно . чтобы учащиеся грамотно выполняли чертеж

Умели выделить криволинейную трапецию и вычислять ее площадь

Запись в тетрадь, сопровождается устными комментариями

Задача 2 учебника – рисунок на слайде

Ученик решает на доске

Какая фигура называется криволинейной трапецией?
Как найти площадь криволинейной трапеции?

Ответы устно, можно использовать при ответе записи в тетради

Выставление отметок за урок

С комментарием за что и почему. Оценка работы всего класса

Откройте учебник на стр №

Посмотрите, пожалуйста, на домашнее задание . Какие у вас еще есть вопросы?

Консультация по выполнению домашней работы

обратить внимание на обязательное построение графика. И выделения криволинейной трапеции

Предварительный просмотр:

Подписи к слайдам:

Площадь криволинейной трапеции и интеграл . у х Учитель математики Ванина Валентина Анатольевна

a b х=а x=b 0 y = f(x) Х У Криволинейная трапеция Отрезок [ a;b ] называют основанием этой криволинейной трапеции Криволинейной трапецией называется фигура, ограниченная графиком непрерывной и не меняющей на отрезке [ а;b ] знака функции f ( х ) , прямыми х=а , x=b и отрезком [ а;b ].

Криволинейная трапеция 0 2 0 0 0 1 -1 -1 2 -1 -2 У=х²+2х У=0,5х+1

Какие из заштрихованных на рисунке фигур являются криволинейными трапециями, а какие нет? Заполнить таблицу №1 Да/нет №2 №3 №4 №5 №6

0 х у 1 Не верно 0 х 0 х 0 х 0 х 0 х у у у у у У=1 2 верно 3 3 y = f(x ) y = f(x ) y = f(x ) y = f(x ) y = f(x ) y = f(x ) У=3 4 5 6 Не верно Не верно верно верно

№999(1 ). Изобразить криволинейную трапецию, ограниченную графиком функции y = (x- 1 ) 2 , осью Ox и прямой x =2 . x = 2

Площадь криволинейной трапеции. где F(x) – любая первообразная функции f(x) .

Формула Ньютона-Лейбница 1643—1727 1646—1716

Найти площадь криволинейной трапеции, изображенной на рисунке 0 1 3 У=х ² 1

Найти площадь криволинейной трапеции, изображенной на рисунке 0 y = sinx I I 1 -1

По теме: методические разработки, презентации и конспекты

Открытый урок в 11 классе "Площадь криволинейной трапеции"

На уроке обобщен материал по нахождению площади криволинейной трапеции через первообразную и интеграл..Материал полезен для формирования умений и навыков нахождения площади криволинейной трапеции при .

Площадь криволинейной трапеции и интеграл

Презентация к уроку в 11 классе.

Урок по алгебре и началам анализа в 11 классе "Площадь криволинейной трапеции и интеграл"

Урок по алгебре и началам анализа в 11 классе "Площадь криволинейной трапеции и интеграл".

Площадь криволинейной трапеции и интеграл.

Презентация к уроку по теме "Площадь криволинейной трапеции и интеграл". Материал для 11 класса. В презентации представлена лаконичная теоритическая часть и несколько решенных заданий по зад.

Презентация по алгебре в 11 классе на тему "Площадь криволинейной трапеции и интеграл"

Презентация по алгебре в 11 классе на тему "Площадь криволинейной трапеции и интеграл".

Материал для урока в 11 классе "Площадь криволинейной трапеции"

Материал для урока в 11 классе "Площадь криволинейной трапеции". Задания на повторение темы "Применение производной", а также разбор задач на вычисление площади криволинейной трапе.

Для учеников 1-11 классов и дошкольников
Бесплатные сертификаты учителям и участникам

Выберите документ из архива для просмотра:

Выбранный для просмотра документ Консект урока Площадь криволинейной трапеции и интеграл.docx

Урок в 11 общеобразовательном классе. Урок рассчитан на 90 минут.

Педагогические технологии: развитие критического мышления, здоровьесбережения, развивающего обучения, развитие творческих способностей.

Цель урока: ввести понятие криволинейной трапеции;

ввести формулу нахождения площади криволинейной трапеции;

ознакомить с понятием интеграла.

Источники информации и оборудование:

Учебник Алгебра и начала математического анализа 11 класс, Ю.М. Колягин и др.

ИД PolyVisionEno , компьютер.

Цель педагогической деятельности :

дидактическая цель - создать условия для понимания необходимости знать формулу Ньютона – Лейбница, для формирования умения применять эту формулу для нахождения площади криволинейной трапеции, конструктивного решения учебных проблем, развития внутренней мотивации учения школьников;

цели по содержанию:

обучающие – отработать умение определять к риволинейную трапецию и находить её площадь;

развивающие – развивать умения анализировать, сравнивать, обобщать, делать выводы, развивать внимательность;

воспитательные – развивать познавательный интерес учащихся через использование ИКТ, способствовать формированию умения слушать одноклассников, понимания важной роли настойчивости для достижения цели.

Задачи педагогической деятельности :

научить школьников применять формулу Ньютона – Лейбница для нахождения площади криволинейной трапеции.

Слайд №1. Что вы видите на слайде? (Криволинейная трапеция. Даём определение)

Постановка проблемы . Криволинейная трапеция – часть плоскости. Как и для любой плоской фигуры можно найти её площадь. Как это сделать? Проблема!

Какова цель нашего урока? (Научиться находить площадь криволинейной трапеции)

Слайд №3 . Ещё раз посмотрим на вид криволинейной трапеции, и на её определение.

Слайд №4. Примеры криволинейных трапеций.

Слайды №5,6 . Интерактивное задание. Цель: научится определять криволинейную трапецию. Какие из заштрихованных на рисунке фигур являются криволинейными трапециями, а какие нет?

Слайд №7. Интерактивное задание. Цель: научится изображать криволинейную трапецию. Изобразить криволинейную трапецию, ограниченную графиком функции y = ( x - 1 ) 2 , осью Ox и прямой x =2.

Слайд №8 . Изобразим криволинейную трапецию. Формула площади криволинейной трапеции.

Слайд №9 . Отдых для глаз.

Слайды №10,11 . Задание из ФИПИ. Цель: подготовка к ЕГЭ. Найти площадь фигуры.

Работа по учебнику. Стр.143, №14(4,6). Цель: отработка формулы площади криволинейной трапеции.

Работа с учебником. Цель: ввести понятие определённого интеграла. Стр.138. Рассмотрим рис. 87 – 89. Нахождение площади криволинейной трапеции сводится к нахождению суммы площадей прямоугольников. Ученик читает текст на стр.139: понятие интегральной суммы. Предел этой интегральной суммы называют определённым интегралом от функции f ( x ) на отрезке .

Слайд №12 . Формула площади криволинейной трапеции через интеграл.

Слайд №13. Формула Ньютона – Лейбница.

Слайд №14. Формула Ньютона – Лейбница в удобном для вычисления интеграла виде.

Работа по учебнику. Стр.139, рис. 90. Найти площадь закрашенной фигуры. Цель: отработать умение находить площадь криволинейной трапеции с помощью интеграла.

Работа по учебнику Стр.143, №15(2,6,8). Цель: отработать умение находить площадь криволинейной трапеции с помощью интеграла

Повторение. Цель: подготовка к ЕГЭ. Задания из ФИПИ.

Домашнее задание. Стр. 137,пар.3,№14(1,5), №15(3),№17(н/ч), фипи – начала анализа-стр.21 - № A6AEC1, стр.23 - № E6AE34

Выбранный для просмотра документ Презентация Площадь криволинейной трапеции и интеграл.pptx

Описание презентации по отдельным слайдам:

Криволинейная трапеция Отрезок [a;b] называют основанием этой криволинейной трапеции Криволинейной трапецией называется фигура, ограниченная графиком непрерывной и не меняющей на отрезке [а;b] знака функции f(х), прямыми х=а, x=b и отрезком [а;b]. Х У Анимация по щелчку мыши

Площадь криволинейной трапеции и интеграл. у х

Криволинейная трапеция 0 2 0 0 0 1 -1 -1 2 -1 -2 У=х²+2х У=0,5х+1

Какие из заштрихованных на рисунке фигур являются криволинейными трапециями, а какие нет? Задание для заполнения таблицы на следующем слайде

у 1 Не верно у у у у у У=1 2 верно 3 3 y = f(x) y = f(x) y = f(x) y = f(x) y = f(x) y = f(x) У=3 4 5 6 Не верно Не верно верно верно 0 х 0 х 0 х 0 х 0 х 0 х Для проверки триггер – нажать на кнопку с № ответа (верно/неверно)

Изобразить криволинейную трапецию, ограниченную графиком функции y = (x-1)2, осью Ox и прямой x=2. x = 2 Анимация по щелчкам –построение графика – сдвиг оси ОУ на 1 влево

Площадь криволинейной трапеции. где F(x) – любая первообразная функции f(x). Анимация по щелчку

ФИПИ – начала математического анализа стр.24 -№CFC988

ФИПИ – начала математического анализа стр.21 -№5FB49C

Формула Ньютона-Лейбница 1643—1727 1646—1716 Лейбниц Готфрид Вильгельм Исаак Ньютон

F(b) –F(a)=F(x) b a F(x) = b a F(b) –F(a)

Определенный интеграл И. Ньютон Г. Лейбниц где Формула Ньютона - Лейбница

Найти площадь криволинейной трапеции, изображенной на рисунке 0 1 3 У=х² 1 Решение – анимация по щелчку

Краткое описание документа:

подготовка к ЕГЭ/ОГЭ и ВПР
по всем предметам 1-11 классов

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Сейчас обучается 682 человека из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

ЗП до 91 000 руб.
Гибкий график
Удаленная работа

Дистанционные курсы для педагогов

Свидетельство и скидка на обучение каждому участнику

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 607 326 материалов в базе

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

Свидетельство и скидка на обучение каждому участнику

Другие материалы

Вам будут интересны эти курсы:

Оставьте свой комментарий

11.02.2018 5645
RAR 1.4 мбайт
482 скачивания
Рейтинг: 5 из 5
Оцените материал:

Настоящий материал опубликован пользователем Игошкина Елена Викторовна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

40%

Подготовка к ЕГЭ/ОГЭ и ВПР
Для учеников 1-11 классов

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Минтруд предложил упростить направление маткапитала на образование

Время чтения: 1 минута

В Россию приехали 10 тысяч детей из Луганской и Донецкой Народных республик

Время чтения: 2 минуты

Школы граничащих с Украиной районов Крыма досрочно уйдут на каникулы

Время чтения: 0 минут

Онлайн-тренинг: нейрогимнастика для успешной учёбы и комфортной жизни

Время чтения: 2 минуты

Академическая стипендия для вузов в 2023 году вырастет до 1 825 рублей

Время чтения: 1 минута

Отчисленные за рубежом студенты смогут бесплатно учиться в России

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

В данном видеоуроке мы узнаем, что называют криволинейной трапецией. Выясним, как можно вычислить площадь криволинейной трапеции. Узнаем, что называют интегралом от функции f(x) на отрезке [a; b].

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.

Получите невероятные возможности

Конспект урока "Площадь криволинейной трапеции и интеграл"

Сегодня на уроке мы узнаем, что называют криволинейной трапецией. Выясним, как можно вычислить площадь криволинейной трапеции. Узнаем, что называют интегралом от функции на отрезке .

А сейчас рассмотрим фигуру, которая ограничена снизу отрезком оси . Сверху ограничена графиком непрерывной функции такой, что при и при . С боков фигура ограничена отрезками прямых и . Эту фигуру называют криволинейной трапецией.

Отрезок называют основанием этой криволинейной трапеции.

Выясним, как можно вычислить площадь этой фигуры с помощью первообразной функции .

Итак, пусть – площадь криволинейной трапеции, основанием которой является отрезок , где – любая точка отрезка .

При отрезок вырождается в точку, поэтому .

При имеем . – площадь криволинейной трапеции.

Покажем, что является первообразной функции , то есть .

Рассмотрим , где .

Отметим, что случай, когда , рассматривается аналогично.

Эта разность равна площади криволинейной трапеции, основанием которой является отрезок .

Справедливо следующее утверждение: найдётся точка такая, что указанная площадь равна площади прямоугольника с основанием и высотой , то есть справедливо равенство .

Отметим, что строгое доказательство данного утверждения рассматривается в курсе высшей математики.

Пусть , тогда и , так как – непрерывная функция.

, при . То есть .

Таким образом, мы показали, что является первообразной функции .

Любая другая первообразная функции отличается от на постоянную, то есть .

При из этого равенства получаем . Так как , то . Тогда равенство можно записать так: .

Отсюда получаем .

Итак, площадь криволинейной трапеции можно вычислить по формуле , где – любая первообразная функции .

Получается, что вычисление площади криволинейной трапеции сводится к отысканию первообразной функции , то есть к интегрированию функции .

Эту формулу называют формулой Ньютона – Лейбница в честь создателей дифференциального и интегрального исчисления: Исаака Ньютона и Готфрида Вильгельма Лейбница.

Обратите внимание, что правую часть формулы часто записывают вот таким образом: . В таком случае формула примет вид .

Числа и называют соответственно нижним и верхним пределами интегрирования. Функцию называют подынтегральной функцией. Переменную называют переменной интегрирования.

Далее из двух формул мы получаем, что .

Давайте с вами вычислим площадь криволинейной трапеции, ограниченной графиком функции , осью и прямыми и .

Приведённые формулы также справедливы в случаях, когда функция положительна внутри отрезка , а на одном из концов отрезка или на обоих концах равна нулю.

Найдём площадь криволинейной трапеции, изображённой на рисунке.

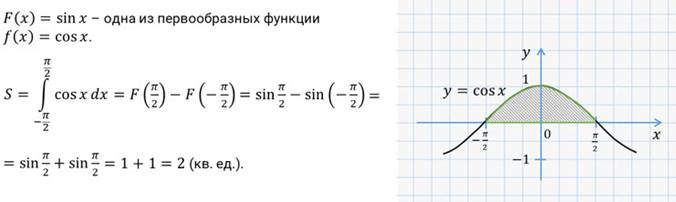
Вообще, исторически интеграл возник в связи с вычислением площадей фигур, которые ограничены кривыми, в частности с вычислением площади криволинейной трапеции. Этому будет посвящено одно из наших следующих занятий.

Давайте рассмотрим рисунок. Здесь изображена криволинейная трапеция, ограниченная прямыми , , осью и графиком функции . Основание этой криволинейной трапеции – отрезок .

Разобьём его на отрезков точками , , , …, . При этом обратите внимание, что эти отрезки не обязательно должны быть равными. Через эти точки проведём вертикальные прямые.

Теперь на каждом отрезке , где , выберем точку и обозначим .

Тогда площадь прямоугольника с основанием и равна .

А вот площадь рассматриваемой криволинейной трапеции приближённо равна сумме площадей построенных прямоугольников:

. Эту сумму называют интегральной суммой функции на отрезке .

Мы можем увеличивать число точек разбиения отрезка так, чтобы наибольшая из длин отрезков стремилась к нулю.

В курсе высшей математики доказывается, что для любой непрерывной функции (не обязательно неотрицательной) на отрезке интегральные суммы стремятся к некоторому числу, то есть имеют предел, не зависящий от выбора точек . Этот предел называют интегралом (определённым интегралом) от функции на отрезке и обозначают .

А теперь давайте выполним задание. Найдите площадь криволинейной трапеции, ограниченной прямыми , , осью и графиком функции :

Читайте также: