Конспект урока описанная окружность

Обновлено: 06.07.2024

Предметные - познакомить учащихся с понятиями вписанной и описанной окружностей треугольника и их свойствами.

Личностные - формировать интерес к изучению темы и желание применять приобретённые знания и умения.

Метапредметные - формировать умение использовать приобретённые знания в практической деятельности.

( Проверка домашнего задания, наличия учебников и тетрадей. Урок проводится с помощью презентации ).

Устный опрос . 1) Что такое окружность?

2) Дайте определение треугольника?

3) Что такое перпендикуляр?

4) Что такое серединный перпендикуляр?

5) Что такое касательная?

6) Что такое биссектриса треугольника?

III. Постановка цели и задач урока. Мотивация учебной деятельности .

IV. Изучение нового материала.

Определение: Окружность называют описанной около треугольника, если она проходит через все вершины этого треугольника.

Говорят также, что треугольник вписан в окружность.

Теорема 21.1 Около любого треугольника можно описать окружность.

Практическая работа. Построить произвольный треугольник АВС. Провести серединные перпендикуляры m и n и k к сторонам АВ, АС и ВС соответственно. Что можно сказать о взаимном расположении серединных перпендикуляров?

Следствие 1. Три серединных перпендикуляра сторон треугольника пересекаются в одной точке.

Обозначить точку пересечения буквой О. Т. к. точка О принадлежит серединному перпендикуляру m, то ОА=ОВ. Поскольку точка О принадлежит серединному перпендикуляру n, то ОА=ОС. Значит ОА=ОС=ОВ, т. е. тоска О равноудалена от всех вершин треугольника.

Около треугольника можно описать только одну окружность, т. к. серединные перпендикуляры имеют только одну точку пересечения.

Провести окружность с центром в точку О. Что можно сказать о взаимном расположении треугольника и окружности?.

Следствие 2. Центр окружности, описанной около треугольника, – это точка пересечения серединных перпендикуляров его сторон.

Определение: Окружность называют вписанной в треугольник, если она касается всех его сторон.

В этом случае также говорят, что треугольник описан около окружности.

Точка О (рис. 301) — центр вписанной окружности треугольника АВС, отрезки ОМ, ON, OP - радиусы, проведённые в точки касания,
ОМ AB, ON ВС, OP AC. Поскольку ОМ = ON=OP, то центр вписанной окружности треугольника равноудалён от всех его сторон.

Теорема 21.2 В любой треугольник можно вписать окружность.

Практическая работа . Построить произвольный треугольник АВС. Провести биссектрисы углов А и В., Обозначить точку их пересечения буквой О. Т. к. точка О принадлежит биссектрисе угла А, то она равноудалена от сторон АВ и АС.(теорема 19.2). Аналогично, так как точка О принадлежит биссектрисе угла В, то она равноудалена от сторон ВА и ВС. Следовательно, точка О равноудалена от всех сторон треугольника.

Заметим, что в треугольник можно вписать только одну окружность.
Это следует из того, что биссектрисы углов А и В (см. рис. 302) пересекаются только в одной точке. Следовательно, существует только одна точка,
равноудалённая от сторон треугольника.

Следствие 1. Биссектрисы углов треугольника пересекаются в одной
точке.

Следствие 2.Центр окружности, вписанной в треугольник, — это точка
пересечения его биссектрис.

Для учеников 1-11 классов и дошкольников
Бесплатные сертификаты учителям и участникам

Ввести понятие описанной около многоугольника окружности.

Рассмотреть теорему об окружности, описанной около треугольника и показать ее применение при решении задач.

Совершенствовать навыки решения задач.

I .Организационный момент

Сообщить тему урока, сформулировать цели урока

II . Актуализация знаний учащихся и подготовка к восприятию нового материала.

Решение задач по готовым чертежам.

III . Изучение нового материала

Ввести понятие окружности, описанной около многоугольника и многоугольника, вписанного в окружность. (См. файл)

Ввести понятие окружности , описанной около треугольника и треугольника, вписанного в окружность. (См. файл)

Доказать теорему, об окружности, описанной около треугольника. (См. файл)

Рассмотреть вопрос об окружности, описанной около четырех угольника. Свойство вписанного четырехугольника. (См. файл)

IV . Закрепление изученного материала

В рабочих тетрадях решить самостоятельно задачи №110, 111. Учитель оказывает индивидуальную помощь нуждающимся учащимся.

Разобрать коллективно задачи № 704, 706.

Решить самостоятельно задачи № 702 (а), 703.

№ 703 ( два случая):

V . Подведение итогов урока

Оценить работу учащихся.

VI . Задание на дом

п 75,вопросы 24, 25;

Решить задачи № 702 (б), 705 (б), 707, 711

подготовка к ЕГЭ/ОГЭ и ВПР
по всем предметам 1-11 классов

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Сейчас обучается 933 человека из 80 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Сейчас обучается 683 человека из 75 регионов

Курс повышения квалификации

Инструменты онлайн-обучения на примере программ Zoom, Skype, Microsoft Teams, Bandicam

Курс добавлен 31.01.2022
Сейчас обучается 24 человека из 17 регионов

ЗП до 91 000 руб.
Гибкий график
Удаленная работа

Дистанционные курсы для педагогов

Свидетельство и скидка на обучение каждому участнику

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 608 475 материалов в базе

Материал подходит для УМК

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

Свидетельство и скидка на обучение каждому участнику

Другие материалы

Вам будут интересны эти курсы:

Оставьте свой комментарий

26.03.2019 2403
DOCX 1.4 мбайт
195 скачиваний
Оцените материал:

Настоящий материал опубликован пользователем Маврина Татьяна Васильевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

40%

Подготовка к ЕГЭ/ОГЭ и ВПР
Для учеников 1-11 классов

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Минпросвещения России подготовит учителей для обучения детей из Донбасса

Время чтения: 1 минута

В Россию приехали 10 тысяч детей из Луганской и Донецкой Народных республик

Время чтения: 2 минуты

Каждый второй ребенок в школе подвергался психической агрессии

Время чтения: 3 минуты

Отчисленные за рубежом студенты смогут бесплатно учиться в России

Время чтения: 1 минута

Школы граничащих с Украиной районов Крыма досрочно уйдут на каникулы

Время чтения: 0 минут

Минтруд предложил упростить направление маткапитала на образование

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

В этом уроке мы узнаем, что если все вершины многоугольника лежат на окружности, то окружность называется описанной около многоугольника, а многоугольник – вписанным в эту окружность. Докажем, что около любого треугольника можно описать окружность. А вот, что около четырехугольника не всегда можно описать окружность. И также узнаем, что в любом вписанном четырехугольнике сумма противоположных углов равна 180°.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.

Получите невероятные возможности

Конспект урока "Описанная окружность"

На этом уроке мы узнаем, какую окружность называют описанной. Докажем, что около любого треугольника можно описать окружность. А также покажем, что около четырехугольника не всегда можно описать окружность.

Ранее мы с вами рассматривали вписанные углы. Напомню, что угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным углом. Если есть вписанный угол BAC и дуга BMC расположена внутри этого угла, то говорят, что вписанный угол BAC опирается на дугу BMC.

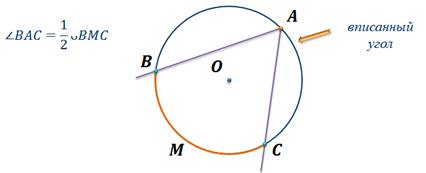
Также мы знаем, что вписанный угол измеряется половиной дуги, на которую он опирается.

Определение. Если все вершины многоугольника лежат на окружности, то окружность называется описанной около многоугольника, а многоугольник – вписанным в эту окружность.

Докажем теорему об окружности, описанной около треугольника.

Теорема. Около любого треугольника можно описать окружность.

Доказательство.

Окружность проходит через все три вершины .

Окружность описана около .

Теорема доказана.

1. Около любого треугольника можно описать только одну окружность.

Доказательство.

Допустим, около треугольника можно описать две окружности.

Тогда центр каждой из них равноудален от его вершин и поэтому совпадает с точкой пересечения серединных перпендикуляров, проведенных к сторонам треугольника.

Радиус равен расстоянию от точки до вершин треугольника.

Следовательно, эти окружности совпадают.

2. В отличие от треугольника около четырехугольника не всегда можно описать окружность.

Если же около четырехугольника можно описать окружность, то его углы обладают следующим замечательным свойством:

В любом вписанном четырехугольнике сумма противоположных углов равна .

Доказательство.

Рассмотрим четырехугольник .

Докажем, что .

и , то

Значит, сумма противоположных углов вписанного четырехугольника равна .

Что и требовалось доказать.

Аналогично доказывается, что
. Это можно доказать и другим путем. Мы знаем, что сумма внутренних углов выпуклого четырехугольника равна 360º. Как мы уже доказали выше, сумма . Значит, на сумму двух других углов (угла B и угла D) остается тоже 180º

Верно и обратное утверждение. Если сумма противоположных углов четырехугольника равна , то около него можно описать окружность.

Доказательство

Рассмотрим четырехугольник .

Пусть .

Докажем, что эта окружность проходит также через вершину .

1) Вершина может быть расположена внутри круга.

2) Вершина расположена вне круга.

Тогда в четырехугольнике будем иметь

Получили, что .

Следовательно, вершина лежит на окружности.

Что и требовалось доказать.

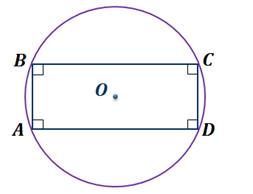
Как вы думаете, около прямоугольника можно описать окружность? Да! Ведь мы знаем, что у прямоугольника все углы равны девяноста градусам. А значит, сумма его противоположных углов составляет сто восемьдесят градусов. Следовательно, около прямоугольника можно описать окружность.

Задача. Найдите стороны остроугольного равнобедренного треугольника, если высота, проведенная к его основанию, равна см, а радиус окружности, в которую он вписан см.

Пусть ABC – равнобедренный треугольник AB=BC, точка O – центр описанной около него окружности. BM высота треугольника ABC. Значит, она перпендикулярна стороне AC.

(см)

Рассмотрим .

– прямоугольный.

(см).

Ответ: , (см).

Давайте рассмотрим рисунок к задаче и укажем, где находится центр окружности описанной около треугольника. Проведем серединные перпендикуляры к сторонам треугольника.

Напомним, что серединные перпендикуляры к сторонам треугольника, пересекаются в одной точке. Мы с вами уже говорили, что, так как треугольник ABC равнобедренный по условию, то высота BM является и его медианой, то есть она является и серединным перпендикуляром к стороне AC. Заметим, что точка пересечения серединных перпендикуляров совпала с центром окружности описанной около треугольника.

Следовательно, верно утверждение: перпендикуляры, восстановленные к серединам сторон треугольника (серединные перпендикуляры) пересекаются в одной точке, которая является центром описанной окружности.

На этом уроке мы узнали, что если все вершины многоугольника лежат на окружности, то окружность называется описанной около многоугольника, а многоугольник – вписанным в эту окружность. Доказали, что около любого треугольника можно описать окружность. А вот, что около четырехугольника не всегда можно описать окружность. И также узнали, что в любом вписанном четырехугольнике сумма противоположных углов равна 180º.

Введем новое понятие: описанная окружность.
Определение: если все вершины многоугольника лежат на окружности, то окружность называется описанной около многоугольника, а многоугольник – вписанным в эту окружность.

На рисунке четырёхугольник MNKP вписан в окружность с центром O, так как все его вершины лежат на этой окружности.

На рисунке четырёхугольник ABCD не является вписанным в окружность, т.к. вершина C не лежит на окружности.
Рассмотрим треугольник АВС и впишем его в окружность. Всегда ли это возможно сделать?

Докажем теорему: Около любого треугольника можно описать окружность.
Дано: ∆ABC
Доказать: существует окружность, что A, B, C принадлежат этой окружности.
Доказательство:
Построим в треугольнике серединные перпендикуляры к сторонам и обозначим точку их пересечения О.

По свойству серединных перпендикуляров точка О равноудалена от точек А, В и С, т.е. OA = OB = OC.

Поэтому окружность с центром в точке О и радиусом ОА проходит через все три вершины треугольника, а значит является описанной около треугольника АВС.
Треугольник ABC вписан в окружность с центром O.
Что и требовалось доказать.
Четырехугольник, вокруг которого можно описать окружность обладает свойством: в любом вписанном четырёхугольнике сумма противоположных углов равна 180°.

Дано: ABCD вписанный четырехугольник.
Доказать:
∠B + ∠D = 180° и ∠A + ∠C = 180°.
Доказательство:
Рассмотрим вписанный угол АВС. Его градусная мера равна ∠ABC = 0,5 ∙ ∪ADC.
Градусная мера вписанного угла ADC равна ∠ADC = 0,5 ∙ ∪ABC.
Сумма углов АВС и ADC равна
∠ABC + ∠ADC = 0,5(∪ADC + ∪ABC) = 0,5 ∙ 360° = 180°.
Что и требовалось доказать.
Обратное утверждение также верно. Докажите его самостоятельно:
Если сумма противоположных углов четырехугольника равна 180°, то около него можно описать окружность.
Геометрия, 7-9: учеб. для общеобразоват. учреждений/ [Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др.]. – М.: Просвещение, 2017.

Читайте также: