Функция e x ее свойства и график конспект

Обновлено: 05.07.2024

Урок открытия особенной показательной функции, основание которой - новое число.

Вложение	Размер
arhiv_zip_-_winrar.zip	2.43 МБ

Предварительный просмотр:

Грудинина Мария Михайловна

Тема и номер урока в теме

Цель урока: Организация деятельности учащихся по формированию

-способствовать продолжению развития мыслительных умений: сравнения, анализа, синтеза, вывода; умений самостоятельно добывать знания

- способствовать воспитанию интереса к предмету, воспитанию творческой деятельности учащихся.

Тип урока: урок изучения нового материала
Методы: проблемный,частично-поисковый
Формы работы: коллективный диалог, фронтальная, индивидуальная
Оборудование: проектор, сопровождающая урок презентация
Структура и ход урока

(мотивация, проблемная ситуация, формулирование темы урока, учебной задачи)

Ребята, сегодня на уроке у нас гости- учителя, увлечённые математикой и преподающие её

К сегодняшнему уроку этим ребятам было предложено найти описание на языке математики некоторых процессов в природе или технике

Много трудных математических задач приходится решать в теории межпланетных путешествий. Одной из них является задача об определении массы топлива, необходимого для того, чтобы придать ракете нужную скорость v. Эта масса М зависит от массы m самой ракеты (без топлива) и от скорости v 0 , с которой продукты горения вытекают из ракетного двигателя, например, для того чтобы ракете с массой 1,5 т придать скорость 8000 м/с, надо при скорости истечения газов 2000 м/с взять примерно 80 т топлива. По какой формуле были произведены расчёты?

Одна комнатная муха может за лето произвести 8*

10 особей потомства. Их вес составил бы несколько млн. тонн, они бы заняли огромное пространство, а если их выстроить в цепочку, то их длина будет больше, чем расстояние от Земли до Солнца.

Завезённые в своё время в Австралию кролики стали экологической катастрофой для этого уникального региона.

Можно ли на языке математики описать процесс органического размножения?

Сейчас много говорят об информационном буме. Поток информации захлестывает: утверждают, что ее количество удваивается каждые десять лет.

Декада за декадой — избранные нами значения аргумента выстроятся по горизонтальной оси в порядке равномерного нарастания, по закону арифметической прогрессии: один, два, три, четыре… Значения функции отложатся над ними, возрастая каждый раз вдвое — по закону геометрической прогрессии: два, четыре, восемь, шестнадцать… (Нетрудно заметить, что эти числа представляют собой последовательные степени двойки — первую, вторую, третью, четвертую и так далее.)

А что если посмотреть, как нарастал поток информации до того года, который принят за начальный? Столь же равномерно, откладывая единицу за единицей, пройдемся по оси абсцисс влево от начала координат и над отложенными значениями аргумента будем наносить на график значения функции уже в порядке убывания — вдвое с каждым шагом.

Теперь соединим все нанесенные точки непрерывной гладкой линией — ведь количество информации нарастает от десятилетия к десятилетию плавно, а не скачками.

Как выглядит на языке математике описанный процесс?)

Ребятам базовой группы было предложено задание-исследование, связанное с графиками показательных функций

(Построить графики функций: у=2, у=3, у=10.

В точке х=0 провести касательную к каждому графику. Измерить транспортиром угол, образованный касательной и положительным направлением оси х. Сделать вывод о зависимости между значением основания показательной функции и градусной мерой угла.)

Изучающим математику – теоретическое задание (повторить основные правила вычисления производной и алгоритмы исследования функции с помощью производной)

Рассмотрим полученную закономерность:

Рассмотрим найденные закономерности:

T=(T 1 -T 0 )e -kt +T 1 ,

M=m(e v/v0 -1) (формула К.Э.Циалковского).

Что общего во всех формулах, описывающих различные процессы? (сл7)

Рассмотренные примеры далеко не исчерпывают использование показательной функции с основанием е для установления закономерностей в природе.

Вы нашли ответы на поставленные вопросы, а вычислять по найденным формулам при известных начальных значениях сумеете? Изобразить графически процессы?

А в чём проблема?

Сформулируйте тему урока, учебную задачу

(что вы хотели бы узнать?) (сл.8)

А как контролируется эта тема на ЕГЭ?

Проанализируйте прототипы задачи В14, которой мы посвящаем следующую консультацию.

На этом уроке рассматривается число е как основание показательной функции. Рассматривается функция y=e^x ее свойства, график, производная.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.

Получите невероятные возможности

Конспект урока "Число е. Функция y=e^x ее свойства, график, дифф."

• рассмотреть число е как основание показательной функции;

• рассмотреть функцию y = e x , её свойства, график и производную.

Прежде чем перейти к изучению нового материала, давайте вспомним основные свойства и график показательной функции.

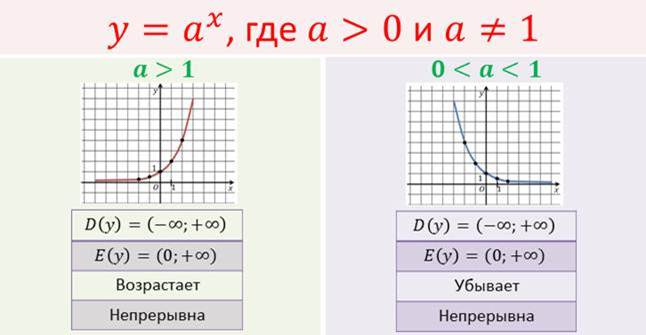
Давайте рассмотрим график функции:

Проведем касательную к точке x = 0.

Если строить точно, а затем измерить угол между касательной и положительным направлением оси Ox, то можно убедиться в том, что:

Теперь давайте построим график функции:

Проведем касательную к точке x = 0.

Если измерить этот угол, то получится:

Если же мы построим график функции:

Проведем касательную к точке x = 0.

Измерим получившийся угол, то получим:

То есть, логично предположить, что есть такое основание а, для которого соответствующий угол между касательной к точке x = 0 и осью абсцисс равен 45°.

Очевидно, что это основание заключено в промежутке от 2 до 3.

Было доказано, что такое число существует, его принято обозначать буквой е. Установлено, что число е – иррациональное, то есть представляет собой бесконечную десятичную непериодическую дробь:

На практике обычно полагают:

Существует множество способов запоминания несколько первых знаков после запятой числа е.

Изобразим график этой функции:

Ее отличие от остальных экспонент будет только в том, что угол между касательной к графику в точке x = 0 и осью абсцисс равен 45°.

По графику легко записать основные свойства функции игрек равно е в степени икс.

Приведены справочные данные по показательной функции – основные свойства, графики и формулы. Рассмотрены следующие вопросы: область определения, множество значений, монотонность, обратная функция, производная, интеграл, разложение в степенной ряд и представление посредством комплексных чисел.

Определение

Показательная функция – это обобщение произведения n чисел, равных a :
y ( n ) = a n = a·a·a···a ,
на множество действительных чисел x :
y ( x ) = a x .
Здесь a – фиксированное действительное число, которое называют основанием показательной функции.
Показательную функцию с основанием a также называют экспонентой по основанию a .

Обобщение выполняется следующим образом.
При натуральном x = 1, 2, 3. , показательная функция является произведением x множителей:
.
При этом она обладает свойствами (1.5-8) (см. ниже ⇓), которые следуют из правил умножения чисел. При нулевом и отрицательных значениях целых чисел , показательную функцию определяют по формулам (1.9-10). При дробных значениях x = m/n рациональных чисел, , ее определяют по формуле(1.11). Для действительных , показательную функцию определяют как предел последовательности:
,
где – произвольная последовательность рациональных чисел, сходящаяся к x : .
При таком определении, показательная функция определена для всех , и удовлетворяет свойствам (1.5-8), как и для натуральных x .

Свойства показательной функции

Показательная функция y = a x , имеет следующие свойства на множестве действительных чисел ( ) :
(1.1) определена и непрерывна, при , для всех ;
(1.2) при a ≠ 1 имеет множество значений ;
(1.3) строго возрастает при , строго убывает при ,
является постоянной при ;
(1.4) при ;
при ;
(1.5) ;
(1.6) ;
(1.7) ;
(1.8) ;
(1.9) ;
(1.10) ;
(1.11) , .

Другие полезные формулы.
.
Формула преобразования к показательной функции с другим основанием степени:

При b = e , получаем выражение показательной функции через экспоненту:

Частные значения

Графики показательной функции

Графики показательной функции y = a x при различных значениях основания a .

На рисунке представлены графики показательной функции
y ( x ) = a x
для четырех значений основания степени: a = 2 , a = 8 , a = 1/2 и a = 1/8 . Видно, что при a > 1 показательная функция монотонно возрастает. Чем больше основание степени a , тем более сильный рост. При 0 1 показательная функция монотонно убывает. Чем меньше показатель степени a , тем сильнее убывание.

Возрастание, убывание

Показательная функция, при является строго монотонной, поэтому экстремумов не имеет. Основные ее свойства представлены в таблице.

y = a x , a > 1	y = a x , 0 1
Область определения	– ∞	– ∞
Область значений	0	0
Монотонность	монотонно возрастает	монотонно убывает
Нули, y = 0	нет	нет
Точки пересечения с осью ординат, x = 0	y = 1	y = 1
+ ∞	0
0	+ ∞

Обратная функция

Обратной для показательной функции с основанием степени a является логарифм по основанию a .

Дифференцирование показательной функции

Для дифференцирования показательной функции, ее основание нужно привести к числу e , применить таблицу производных и правило дифференцирования сложной функции.

Для этого нужно использовать свойство логарифмов
и формулу из таблицы производных:
.

Пусть задана показательная функция:
.
Приводим ее к основанию e :

Применим правило дифференцирования сложной функции. Для этого вводим переменную

Тогда

Из таблице производных имеем (заменим переменную x на z ):
.
Поскольку – это постоянная, то производная z по x равна
.
По правилу дифференцирования сложной функции:
.

Производная показательной функции

Пример дифференцирования показательной функции

Найти производную функции
y = 3 5 x

Выразим основание показательной функции через число e .
3 = e ln 3
Тогда
.
Вводим переменную
.
Тогда

Из таблицы производных находим:
.
Поскольку 5ln 3 – это постоянная, то производная z по x равна:
.
По правилу дифференцирования сложной функции имеем:
.

Интеграл

Выражения через комплексные числа

Рассмотрим функцию комплексного числа z:
f ( z ) = a z
где z = x + iy ; i 2 = – 1 .
Выразим комплексную постоянную a через модуль r и аргумент φ :
a = r e i φ
Тогда

.
Аргумент φ определен не однозначно. В общем виде
φ = φ ₀ + 2 πn ,
где n – целое. Поэтому функция f ( z ) также не однозначна. Часто рассматривают ее главное значение
.

Разложение в ряд

В данной публикации мы рассмотрим, что такое экспонента, как выглядит ее график, приведем формулу, с помощью которой задается экспоненциальная функция, а также перечислим ее основные свойства.

Определение и формула экспоненты

Экспонента – это показательная функция, формула которой выглядит следующим образом:

Экспоненциальная функция (так часто называют экспоненту) может быть определена:

Через предел (lim):

Через степенной ряд Тейлора:

График экспоненты

Ниже представлен график экспоненциальной функции

Как мы видим график (синяя линия) является выпуклым, строго возрастающим, т.е. при увеличении x увеличивается значение y .

Асимптотой является ось абсцисс, т.е. график во II четверти координатной плоскости стремится к оси Ox , но никогда не пересечет и не коснется ее.

Пересечение с осью ординат Oy – в точке , так как

Касательная (зеленая линия) к экспоненте проходит под углом 45 градусов в точке касания.

Читайте также: