Суть метода лагранжа кратко

Обновлено: 16.05.2024

Приведенные выше условия оптимальности (теорема 5), лежат в основе метода множителей Лагранжа. который позволяет свести решение задачи (8) – (9) к решению задачи безусловной оптимизации ее функции Лагранжа. Для этого следует выполнить следующие действия.

1. Составить функцию Лагранжа по формуле (10).

2. Найти стационарные точки функции Лагранжа. Для этого нужно выписать частные производные по всем переменным x_j и λ_i и приравнять их к нулю. Получается система n + m уравнений, представленная формулами (11) – (12). Все ее решения являются стационарными точками функции Лагранжа.

3. Любое решение (x * , λ * ) системы (11) – (12) определяет точку x * , которая может быть локальным оптимумом ЦФ в задаче (8) – (9). Поэтому, найдя все решения системы (11) – (12), мы получим все точки, в которых ЦФ может иметь локальный оптимум.

4. Среди этих точек после дополнительного анализа отбираются такие, которые действительно являются точками локального оптимума. После сравнения значений ЦФ в этих точках находится точка, являющаяся глобальным оптимумом.

Следует иметь в виду, что если (х * , λ * ) — стационарная точка функции Лагранжа, то не обязательно точка х * — локальный оптимум задачи (8) – (9). Это верно лишь тогда, когда исходная задача является задачей ВП. Более того, в этом случае х * — точка глобального оптимума этой задачи. Справедлива следующая теорема.

Теорема 6. Предположим, что задача (8) – (9) является задачей ВП, т.е. все ее ограничения линейные и ищется минимум выпуклой (максимум вогнутой) функции. Тогда, если (х * , λ * ) — решение системы (11) – (12), то х * — точка глобального оптимума задачи (8) – (9).

Обобщенный метод множителей Лагранжа.

Для решения задачи (14) – (15) можно использовать обобщенный метод множителей Лагранжа. Основная идея этого метода заключается в последовательном учете ограничений. Предположим для определенности, что решается задача максимизации ЦФ.
Сначала все ограничения отбрасываются, и решается задача безусловной максимизации ЦФ. Находится ее стационарная точка и проверяется ее допустимость. Если оказалось, что эта точка принадлежит ОДР, то процесс вычислений завершается, так как в силу выпуклости задачи (14) – (15) найденная точка является ее решением.
Если же найденная точка не допустима, то формируется новая задача, которая состоит в максимизации ЦФ с учетом первого ограничения задачи. Однако это ограничение записывается не как неравенство, а как равенство.
Получаем классическую задачу условной оптимизации вида:
Z = f (x₁,…, x_n) → mах,

g₁(x₁,…, x_n) = b₁.
Для ее решения используется метод множителей Лагранжа. Выписывается функция Лагранжа

L(x₁,…, x_n, λ) = f(x₁,…, x_n) + λ(b₁ – g₁ (x₁,…, x_n))
и решается система уравнений, определяющая стационарные точки этой функции:

Если в результате получен вектор решения (x₁*, . , x_n*, λ*) такой, что вектор (x₁*, . , x_n*) допустим в исходной задаче и λ * ≥ 0, то это означает, что (x₁*, . , x_n*) — искомая точка оптимума. Если же оказалось, что λ * Пример . Исследовать точки на экстремум Z=x₁²+x₂²; x₁+x₂=1
Составим функцию Лагранжа: L(x₁, x₂, λ) = x₁²+x₂² + λ(1-x₁-x₂)
Составим необходимые условия существования экстремума

Чтобы оценить, является ли точка экстремальной и какой экстремум она дает, обратимся к достаточному условию существования экстремума функции двух переменных (условию Лежандра-Клебша.
Составим определитель

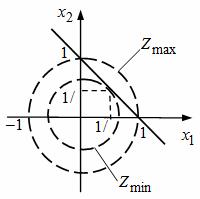
Рис. 2 - Графическое решение
Так как d 2 Z(X*) ⁄ dx₁ 2 >0 и Δ>0_, то в точке X*(½; ½) функция Z достигает минимальное значение. Графическое решение (рис. 2) показывает, что максимальное значение Z_max=1 достигается в точках (x₁=1; x₂=0) и (x₁=0; x₂=1) Таким образом, если бы исходная задача в примере ставилась бы на отыскание максимума, то с помощью решения системы уравнений необходимых условий существования экстремума мы точку максимума бы не определили. Требуется иной подход, который рассмотрим ниже в других разделах.

Рассмотрен способ решения линейных дифференциальных уравнений первого порядка методом вариации постоянной (Лагранжа). Дан пример подробного решения линейного дифференциального уравнения методом Лагранжа.

Рассмотрим линейное неоднородное дифференциальное уравнение первого порядка:
(1) .
Существует три способа решения этого уравнения:

метод интегрирующего множителя;
метод введения двух функций (Бернулли);
метод вариации постоянной (Лагранжа).

Рассмотрим решение линейного дифференциального уравнения первого порядка методом Лагранжа.

Метод вариации постоянной (Лагранжа)

В методе вариации постоянной мы решаем уравнение в два этапа. На первом этапе мы упрощаем исходное уравнение и решаем однородное уравнение. На втором этапе мы заменим постоянную интегрирования, полученную на первой стадии решения, на функцию. После чего ищем общее решение исходного уравнения.

Рассмотрим уравнение:
(1)

Шаг 1 Решение однородного уравнения

Ищем решение однородного уравнения:

Это уравнение с разделяющимися переменными

Разделяем переменные - умножаем на dx , делим на y :

Интегрируем:

Интеграл по y - табличный:

Тогда

Потенцируем:

Заменим постоянную e C на C и уберем знак модуля, что сводится к умножению на постоянную ±1 , которую включим в C :

Шаг 2 Заменим постоянную C на функцию

Теперь заменим постоянную C на функцию от x :
C → u ( x )
То есть, будем искать решение исходного уравнения (1) в виде:
(2)
Находим производную.

По правилу дифференцирования сложной функции:
.
По правилу дифференцирования произведения:

.
Подставляем в исходное уравнение (1):
(1) ;

.
Два члена сокращаются:
;
.
Интегрируем:
.
Подставляем в (2):
.
В результате получаем общее решение линейного дифференциального уравнения первого порядка:
.

Пример решения линейного дифференциального уравнения первого порядка методом Лагранжа

Решаем однородное уравнение:

Разделяем переменные:

Умножим на :

Интегрируем:

Интегралы табличные:

Потенцируем:

Заменим постоянную e C на C и убираем знаки модуля:

Отсюда:

Заменим постоянную C на функцию от x :
C → u ( x )

Находим производную:
.
Подставляем в исходное уравнение:
;
;
Или:
;
.
Интегрируем:
;
Решение уравнения:
.

Для начала рассмотрим случай функции двух переменных. Условным экстремумом функции $z=f(x,y)$ в точке $M_0(x_0;y_0)$ называется экстремум этой функции, достигнутый при условии, что переменные $x$ и $y$ в окрестности данной точки удовлетворяют уравнению связи $\varphi (x,y)=0$.

Метод множителей Лагранжа для функций двух переменных.

Метод множителей Лагранжа состоит в том, что для отыскания условного экстремума составляют функцию Лагранжа: $F(x,y)=f(x,y)+\lambda\varphi(x,y)$ (параметр $\lambda$ называют множителем Лагранжа). Необходимые условия экстремума задаются системой уравнений, из которой определяются стационарные точки:

Достаточным условием, из которого можно выяснить характер экстремума, служит знак $d^2 F=F_^dx^2+2F_^dxdy+F_^dy^2$. Если в стационарной точке $d^2F > 0$, то функция $z=f(x,y)$ имеет в данной точке условный минимум, если же $d^2F 0$, то $d^2F 0$, т.е. имеем условный минимум функции $z=f(x,y)$.

Примечание относительно формы записи определителя $H$. показать\скрыть

Некоторые авторы записывают определитель $H$ в иной форме (с знаком "-"):

В этой ситуации сформулированное выше правило изменится следующим образом: если $H > 0$, то функция имеет условный минимум, а при $H m$):

Обозначив множители Лагранжа как $\lambda_1,\lambda_2,\ldots,\lambda_m$, составим функцию Лагранжа:

Необходимые условия наличия условного экстремума задаются системой уравнений, из которой находятся координаты стационарных точек и значения множителей Лагранжа:

Выяснить, условный минимум или условный максимум имеет функция в найденной точке, можно, как и ранее, посредством знака $d^2F$. Если в найденной точке $d^2F > 0$, то функция имеет условный минимум, если же $d^2F 0.$$

Следовательно, в точке $M_1(1;3)$ функция $z(x,y)=x+3y$ имеет условный максимум, $z_<\max>=z(1;3)=10$.

Аналогично, в точке $M_2(-1;-3)$ найдем:

$$H=8\cdot\left| \begin 0 & x & y\\ x & \lambda & 0 \\ y & 0 & \lambda \end \right|= 8\cdot\left| \begin 0 & -1 & -3\\ -1 & 1/2 & 0 \\ -3 & 0 & 1/2 \end \right|=-40$$

Так как $H 0$. Следовательно, знак $H$ противоположен знаку $\lambda$. Можно и довести вычисления до конца:

Вопрос о характере экстремума в стационарных точках $M_1(1;3)$ и $M_2(-1;-3)$ можно решить и без использования определителя $H$. Найдем знак $d^2F$ в каждой стационарной точке:

Отмечу, что запись $dx^2$ означает именно $dx$, возведённый в вторую степень, т.е. $\left( dx \right)^2$. Отсюда имеем: $dx^2+dy^2>0$, посему при $\lambda_1=-\frac$ получим $d^2F 0$, посему в данной точке функция имеет условный максимум, $z_<\max>=\frac$.

Исследуем характер экстремума в каждой из точек иным методом, основываясь на знаке $d^2F$:

Из уравнения связи $x+y=0$ имеем: $d(x+y)=0$, $dx+dy=0$, $dy=-dx$.

Так как $ d^2F \Bigr|_=10 dx^2 > 0$, то $M_1(0;0)$ является точкой условного минимума функции $z(x,y)=3y^3+4x^2-xy$. Аналогично, $d^2F \Bigr|_=-10 dx^2 0$, то $M_1$ – точка минимума функции $u(x)$, при этом $u_<\min>=u(0)=0$. Так как $u_^(M_2) 0; \; y > 0. \end \right. $$

Все дальнейшие преобразования осуществляются с учетом $x > 0; \; y > 0$ (это оговорено в условии задачи). Из второго уравнения выразим $\lambda=-\frac$ и подставим найденное значение в первое уравнение: $5y-\frac\cdot \frac=0$, $4y^2-x^2=0$, $x=2y$. Подставляя $x=2y$ в третье уравнение, получим: $\frac+\frac-1=0$, $y^2=1$, $y=1$.

Так как $y=1$, то $x=2$, $\lambda=-10$. Характер экстремума в точке $(2;1)$ определим, исходя из знака $d^2F$.

В принципе, здесь можно сразу подставить координаты стационарной точки $x=2$, $y=1$ и параметра $\lambda=-10$, получив при этом:

Однако в других задачах на условный экстремум стационарных точек может быть несколько. В таких случаях лучше $d^2F$ представить в общем виде, а потом подставлять в полученное выражение координаты каждой из найденных стационарных точек:

Подставляя $x=2$, $y=1$, $\lambda=-10$, получим:

Ответ: в точке $(2;1)$ функция имеет условный максимум, $z_<\max>=6$.

В следующей части рассмотрим применение метода Лагранжа для функций большего количества переменных.

Заметили ошибку, опечатку, или некорректно отобразилась формула? Отпишите, пожалуйста, об этом в данной теме на форуме (регистрация не требуется).

при наличии заданных ограничений на ее переменные в виде равенств (т.е. определена область допустимых значений)

Метод множителей Лагранжа позволяет задачу поиска условного экстремума целевой функции на множестве допустимых значений преобразовать к задаче безусловной оптимизации функции.

В случае если функции и непрерывны вместе со своими частными производными, то существуют такие переменные λ не равные одновременно нулю, при которых выполняется следующее условие:

Таким образом, в соответствии с методом множителей Лагранжа для поиска экстремума целевой функции на множестве допустимых значений составляю функцию Лагранжа L(х, λ), которую в дальнейшем оптимизируют:

где λ ˗ вектор дополнительных переменных, называемых неопределенными множителями Лагранжа.

Таким образом, задача нахождения условного экстремума функции f(x) свелась к задаче поиска безусловного экстремума функции L(x, λ).

Далее в соответствии с методом определяют частные производные функции Лагранжа:

Решение данной системы уравнений позволяет определить аргументы функции (Х), при которых значение функции L(x, λ), а также значение целевой функции f(x) соответствуют экстремуму.

Величина множителей Лагранжа (λ) имеет практический интерес в случае, если ограничения представлены в форме со свободным членом уравнения (константой). В этом случае можно рассматривать дальнейшее (увеличение/уменьшение) значения целевой функции за счет изменения значения константы в системе уравнения . Таким образом, множитель Лагранжа характеризует скорость изменения максимума целевой функции при изменении ограничивающей константы.

Существует несколько способов определения характера экстремума полученной функции:

Первый способ: Пусть – координаты точки экстремума, а - соответствующее значение целевой функции. Берется точка , близкая к точке , и вычисляется значение целевой функции :

- Если , то в точке имеет место максимум.

- Если , то в точке имеет место минимум.

Второй способ: Достаточным условием, из которого можно выяснить характер экстремума, является знак второго дифференциала функции Лагранжа . Второй дифференциал функции Лагранжа определяется следующим образом:

Если в заданной точке , то целевая функция f(x) имеет в данной точке условный минимум, если же , то целевая функция f(x) имеет в данной точке условный максимум.

Третий способ: Также характер экстремума функции можно выяснить рассмотрев гессиан функции Лагранжа. Матрица Гессе представляет собой симметричную квадратную матрицу вторых частных производных функции в точке , в которой элементы матрицы симметричны относительно главной диагонали.

Для определения типа экстремума (максимум или минимум функции) можно воспользоваться правилом Сильвестра:

1. Для того, чтобы второй дифференциал функции Лагранжа был знакоположителен необходимо, чтобы угловые миноры функции были положительными . При таких условиях функция в этой точке имеет минимум.

2. Для того, чтобы второй дифференциал функции Лагранжа был знакоотрицателен , необходимо, чтобы угловые миноры функции чередовались, причем первый элемент матрицы должен быть отрицательнsv . При таких условиях функция в этой точке имеет максимум.

Под угловым минором понимаем минор, расположенный в первых k строках и k столбцах исходной матрицы.

Основное практическое значение метода Лагранжа заключается в том, что он позволяет перейти от условной оптимизации к безусловной и, соответственно, расширить арсенал доступных методов решения задачи. Однако задача решения системы уравнений, к которой сводится данный метод, в общем случае не проще исходной задачи поиска экстремума. Такие методы называются непрямыми. Их применение объясняется необходимостью получить решение экстремальной задачи в аналитической форме (допустим, для тех или иных теоретических выкладок). При решении конкретных практических задач обычно используются прямые методы, основанные на итеративных процессах вычисления и сравнения значений оптимизируемых функций.

Методика расчета

1 шаг: Определяем функцию Лагранжа из заданной целевой функции и системы ограничений:

2 шаг: Определение аналитических соотношений (в символьном виде) для поиска безусловного экстремума функции L(x, λ).

3 шаг: Решаем полученную систему линейных или нелинейных уравнений, используя соответствующие методы решения.

4 шаг: Определяем характер экстремума (максимум или минимум целевой функции) по любому из представленных выше методов.

Для того, чтобы добавить Ваш комментарий к статье, пожалуйста, зарегистрируйтесь на сайте.

Метод Лагранжа (дифференциальные уравнения) — У этого термина существуют и другие значения, см. Метод Лагранжа. Метод Лагранжа (метод вариации произвольных постоянных) метод для получения общего решения неоднородного уравнения, зная общее решение однородного уравнения без нахождения… … Википедия

Метод Лагранжа приведения квадратичной формы к каноническому виду — У этого термина существуют и другие значения, см. Метод Лагранжа. Метод Лагранжа метод приведения квадратичной формы к каноническому виду, указанный в 1759 году Лагранжем. Описание Данный метод состоит в последовательном выделении в квадратичной… … Википедия

Метод множителей Лагранжа — Метод множителей Лагранжа, метод нахождения условного экстремума функции , где , относительно ограничений , где меняется от единицы до . Содержание … Википедия

Лагранжа множители — Метод множителей Лагранжа, метод нахождения условного экстремума функции f(x), где , относительно m ограничений , i меняется от единицы до m. Содержание 1 Описание метода … Википедия

Лагранжа функция — Метод множителей Лагранжа, метод нахождения условного экстремума функции f(x), где , относительно m ограничений , i меняется от единицы до m. Содержание 1 Описание метода … Википедия

Лагранжа метод множителей — метод решения задач на Условный экстремум; Л. м. м. заключается в сведении этих задач к задачам на безусловный экстремум вспомогательной функции т. н. функции Лагранжа. Для задачи об экстремуме функции f (х1, x2. xn) при… … Большая советская энциклопедия

ЛАГРАНЖА УРАВНЕНИЯ — механики. 1) Лагранжа уравнения 1 го рода дифференциальные ур ния движения механич. системы, к рые даны в проекциях на прямоугольные координатные оси и содержат т. н. множители Лагранжа. Получены Ж. Лагранжем в 1788. Для голономной системы,… … Физическая энциклопедия

ЛАГРАНЖА УРАВНЕНИЯ — 1) в гидромеханике ур ния движения жидкости (газа) в переменных Лагранжа, к рыми являются координаты ч ц среды. Получены франц. учёным Ж. Лагранжем (J. Lagrange; ок. 1780). Из Л. у. определяется закон движения ч ц среды в виде зависимостей… … Физическая энциклопедия

Лагранжа метод — Лагранжа метод [Lagrangian method] — метод решения ряда классов задач математического программирования с помощью нахождения седловой точки (x*, λ*) функции Лагранжа., что достигается приравниванием нулю частных производных этой функции по… … Экономико-математический словарь

Читайте также: