Сравнение бесконечно больших функций кратко

Обновлено: 05.07.2024

Бесконечно малая — числовая функция или последовательность, которая стремится к нулю.

Бесконечно большая — числовая функция или последовательность, которая стремится к бесконечности определённого знака.

Сравнение бесконечно малых

Допустим, у нас есть бесконечно малые при одном и том же величины и (либо, что не важно для определения, бесконечно малые последовательности).

· Если , то — бесконечно малая высшего порядка малости, чем . Обозначают или β≺α.

· Если , то — бесконечно малая низшего порядка малости, чем . Соответственно или α≺β.

· Если (предел конечен и не равен 0), то бесконечно малая величина имеет -й порядок малости относительно бесконечно малой .

Для вычисления подобных пределов удобно использовать правило Лопиталя.

· При величина имеет высший порядок малости относительно , так как . С другой стороны, имеет низший порядок малости относительно , так как .

С использованием О-символики полученные результаты могут быть записаны в следующем виде .

· то есть при функции и являются бесконечно малыми величинами одного порядка.

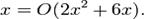
В данном случае справедливы записи и

· При бесконечно малая величина имеет третий порядок малости относительно , поскольку , бесконечно малая — второй порядок, бесконечно малая — порядок 0,5.

Бесконечно малая — числовая функция или последовательность, которая стремится к нулю.

Сравнение бесконечно малых

· Если , то — бесконечно малая высшего порядка малости, чем . Обозначают или β≺α.

· Если , то — бесконечно малая низшего порядка малости, чем . Соответственно или α≺β.

Для вычисления подобных пределов удобно использовать правило Лопиталя.

С использованием О-символики полученные результаты могут быть записаны в следующем виде .

· то есть при функции и являются бесконечно малыми величинами одного порядка.

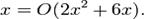
В данном случае справедливы записи и

Сравнение бесконечно больших

Если , то функции и называются бесконечно большими одного и того же порядка.

Функции и называются эквивалентными бесконечно большими при x → a, если λ = 1. Для записи эквивалентности функций используется обозначение вида

Функция называется бесконечно большой более высокого порядка по сравнению с при x → a, если λ = ∞; при этом говорят, что имеет меньший порядок роста.

Если и представляют собой бесконечно большие функции одного и того же порядка, то функция называется бесконечно большой n-го порядка по сравнению с . Например, функция является бесконечно большой 4-го порядка по сравнению с при x → ∞.

Если λ = 0, то бесконечно большие функции и меняются своими ролями. В этом случае функция является бесконечно большой более высокого порядка по сравнению с при x → a.

Отношение а: (2 + sinx) / x = 2 + sinx (если не конечно) Бесконечность). Определение 10.6. Функция v (x) называется b.b. к-й Порядок по w (x) равен x = a, а число k равно Функция rldcom bb v (x) имеет вид x-> a относительно w (x) 1 порядок, когда функции v (x) и wk (x) являются b.b а, если Lim-4? m = c∈R \ . (10.26) bm — функция, функция заказа до 1 bb По сравнению с другим 6.6. Функция не является обязательной Если порядок положительных чисел и функций v (x) относительно w (x) равно & тогда порядок функции v (x) равен «v (x) равно л / к. Не обязательно bb-функция v (x), эквивалентная В каждой степени WK (х), может быть ясно показано Заказать к. Следовательно, функция ax (a> 1) эквивалентна x- * + °°.

Порядок во всех степенях xk (k> 0), но в порядке (10.25) От x до \ + oo рост этой функции на x невозможен. Определение 10.7 Функции Bb v (x) и w (x) как x- + a Когда он называется эквивалентным и указывает от v (x) x до aw (x) предел их отношения в х- \ а равен единице, или 1. (U.27) Функция, эквивалентность как в б.м. Работает симметрично и транзитивно. Заявление 10.1. Функция ограничения отношения 2 bb Равен пределу эквивалентных отношений. В качестве конечного числа функции стригущего лишая x → ∞ Для каждого термина можно указать порядок роста Для х, члены более высокого порядка ( Только) называется основной частью суммы b.b. х- * оо Функция. Следовательно, многочлен степени n Pn (x) = aohp + ahx «-1 + … + an ^ x + an (a ^ φ0)

Это сумма 6,6. как x- * oo функции, то порядок Рост k для каждого члена x Связанный индекс. Поэтому термин oqx71 Более высокий порядок роста (k = n), потому что он уникален, и х- * оо будет основной частью этого общего. Как хорошо Функция X для суммы конечного числа bb — ► может Показать порядок роста для каждого термина Для l / (x-a) члены высшего порядка также в основном Для этого раздела часть такой суммы в х-та Единственное. Например, всего l / sin2z + ctgx две функции bb Согласно x-> 0 (10.18) первое слагаемое является квадратичным. По отношению к 1 / х второй является первичным. так Основная часть этой суммы при x-> 0 равна l / sin2x.

Заявление 10.2.В общем, мы можем говорить о основной части, но не Только конечная алгебраическая сумма x-ba (или х — ► ° °) как функция, а также любая функция в структуре Эквивалент f (x), x-> a и степенной функции A / (x-a) k (X- * оо-степенная функция Axk), AΦ0, k> 0. Степенная функция и основная часть будут 6,6. функция Как x-> a или x-> oo соответственно. Как найти Коэффициент A и индекс k основаны на Использует определение 10.7 и утверждение 10.2 и аналогично процедуре Функция назначения основной части bm.

Образовательный сайт для студентов и школьников

Определения и свойства бесконечно малых и бесконечно больших функций в точке. Связь между ними. Доказательства свойств и теорем. Арифметические свойства пределов с бесконечно малыми и бесконечно большими функциями.

Определение бесконечно малой и бесконечно большой функции

Пусть x ₀ есть конечная или бесконечно удаленная точка: ∞ , –∞ или +∞ .

Определение бесконечно малой функции
Функция α ( x ) называется бесконечно малой при x стремящемся к x ₀ , если функция имеет предел при x → x ₀ , и он равен нулю:
.

Определение бесконечно большой функции
Функция f ( x ) называется бесконечно большой при x стремящемся к x ₀ , если функция имеет предел при x → x ₀ , и он равен бесконечности:
.

Свойства бесконечно малых функций

Свойство суммы, разности и произведения бесконечно малых функций

Сумма, разность и произведение конечного числа бесконечно малых функций при x → x ₀ является бесконечно малой функцией при x → x ₀ .

Теорема о произведении ограниченной функции на бесконечно малую

Произведение функции, ограниченной на некоторой проколотой окрестности точки x ₀ , на бесконечно малую, при x → x ₀ , является бесконечно малой функцией при x → x ₀ .
Доказательство ⇓

Свойство о представлении функции в виде суммы постоянной и бесконечно малой функции

Для того, чтобы функция f ( x ) имела конечный предел , необходимо и достаточно, чтобы
,
где – бесконечно малая функция при x → x ₀ .
Доказательство ⇓

Свойства бесконечно больших функций

Теорема о сумме ограниченной функции и бесконечно большой

Сумма или разность ограниченной функции, на некоторой проколотой окрестности точки x ₀ , и бесконечно большой функции, при x → x ₀ , является бесконечно большой функцией при x → x ₀ .
Доказательство ⇓

Теорема о произведении ограниченной снизу функции на бесконечно большую

Если функция , на некоторой проколотой окрестности точки , по абсолютной величине ограничена снизу положительным числом:
,
а функция является бесконечно большой при x → x ₀ :
,
то их произведение является бесконечно большой функцией при :
.
Доказательство ⇓

Теорема о частном от деления ограниченной функции на бесконечно большую

Если функция f ( x ) является бесконечно большой при x → x ₀ , а функция g ( x ) – ограничена на некоторой проколотой окрестности точки x ₀ , то
.
Доказательство ⇓

Теорема о частном от деления ограниченной снизу функции на бесконечно малую

Если функция , на некоторой проколотой окрестности точки , по абсолютной величине ограничена снизу положительным числом:
,
а функция является бесконечно малой при x → x ₀ :
,
и существует проколотая окрестность точки , на которой , то
.
Доказательство ⇓

Свойство неравенств бесконечно больших функций

Если функция является бесконечно большой при :
,
и функции и , на некоторой проколотой окрестности точки удовлетворяют неравенству:
,
то функция также бесконечно большая при :
.
Доказательство ⇓

Это свойство имеет два частных случая.

Пусть, на некоторой проколотой окрестности точки , функции и удовлетворяют неравенству:
.
Тогда если , то и .
Если , то и .

Связь между бесконечно большими и бесконечно малыми функциями

Из двух предыдущих свойств вытекает связь между бесконечно большими и бесконечно малыми функциями.

Если функция является бесконечно большой при , то функция является бесконечно малой при .

Если функция являются бесконечно малой при , и , то функция является бесконечно большой при .

Связь между бесконечно малой и бесконечно большой функцией можно выразить символическим образом:
, .

Если бесконечно малая функция имеет определенный знак при , то есть положительна (или отрицательна) на некоторой проколотой окрестности точки , то можно записать так:
.
Точно также если бесконечно большая функция имеет определенный знак при , то пишут:
, или .

Тогда символическую связь между бесконечно малыми и бесконечно большими функциями можно дополнить следующими соотношениями:
, ,
, .

Арифметические свойства бесконечно больших и бесконечно малых функций

Приведенные выше свойства выполняются, если функция ограничена, а функция ограничена снизу по абсолютной величине положительным числом. При этом эти функции не обязательно должны иметь конечный предел, а могут расходиться. Однако, эти функции будут обладать указанными свойствами, если они имеют соответствующие пределы. Это позволяет сформулировать арифметические свойства бесконечно больших и бесконечно малых функций.

Пусть существуют пределы функций
и .
И пусть, при , функция является бесконечно малой:
, а функция – бесконечно большой:
.
Тогда существует пределы суммы и разности:
(A.1) ;
существуют пределы произведений:
(A.2) ;
существуют пределы частного:
(A.3) .

Доказательство свойств и теорем

Теорема о произведении ограниченной функции на бесконечно малую

Все свойства ⇑ Произведение функции , ограниченной на некоторой проколотой окрестности точки x ₀ :
при ,
на бесконечно малую , при x → x ₀ :
,
является бесконечно малой функцией при x → x ₀ :
.

Для доказательства этой теоремы, мы воспользуемся определением предела функции по Гейне. А также используем свойство бесконечно малых последовательностей, согласно которому произведение ограниченной последовательности на бесконечно малую является бесконечно малой последовательностью.

Пусть функция является бесконечно малой при :
.
И пусть функция ограничена в некоторой проколотой окрестности точки :
при .

Поскольку существует предел , то существует проколотая окрестность точки , на которой определена функция . Пусть есть пересечение окрестностей и . Тогда на ней определены функции и .

Пусть есть произвольная последовательность, сходящаяся к , элементы которой принадлежат окрестности :
.
Тогда определены последовательности и . Причем последовательность является ограниченной:
,
a последовательность является бесконечно малой:
.

Воспользуемся тем, что произведение ограниченной последовательности на бесконечно малую есть бесконечно малая последовательность:
.
Тогда, согласно определению предела последовательности по Гейне,
.

Свойство о представлении функции в виде суммы постоянной и бесконечно малой функции

Все свойства ⇑ Для того, чтобы функция f ( x ) имела конечный предел , необходимо и достаточно, чтобы
,
где – бесконечно малая функция при x → x ₀ .

Необходимость. Пусть функция имеет в точке конечный предел
.
Рассмотрим функцию:
.
Используя свойство предела разности функций, имеем:
.
То есть есть бесконечно малая функция при .

Теорема о сумме ограниченной функции и бесконечно большой

Все свойства ⇑ Сумма или разность ограниченной функции, на некоторой проколотой окрестности точки x ₀ , и бесконечно большой функции, при x → x ₀ , является бесконечно большой функцией при x → x ₀ .

Для доказательства теоремы, мы воспользуемся определением предела функции по Гейне. Также используем свойство бесконечно больших последовательностей, согласно которому сумма или разность ограниченной последовательности и бесконечно большой является бесконечно большой последовательностью.

Пусть функция является бесконечно большой при :
.
И пусть функция ограничена в некоторой проколотой окрестности точки :
при .

Поскольку существует предел , то существует проколотая окрестность точки , на которой функция определена. Пусть есть пересечение окрестностей и . Тогда на ней определены функции и .

Поскольку сумма или разность ограниченной последовательности и бесконечно большой является бесконечно большой последовательностью, то
.
Тогда, согласно определению предела последовательности по Гейне,
.

Теорема о произведении ограниченной снизу функции на бесконечно большую

Все свойства ⇑ Если функция , на некоторой проколотой окрестности точки , по абсолютной величине ограничена снизу положительным числом:
,
а функция является бесконечно большой при x → x ₀ :
,
то их произведение является бесконечно большой функцией при :
.

Для доказательства этого свойства, мы воспользуемся определением предела функции по Гейне. Также используем свойство бесконечно больших последовательностей, согласно которому произведение бесконечно большой и ограниченной снизу последовательности является бесконечно большой последовательностью.

Пусть функция является бесконечно большой при :
.
И пусть функция ограничена по абсолютной величине снизу положительным числом, на некоторой проколотой окрестности точки :
при .

Поскольку существует предел функции при , то существует проколотая окрестность точки , на которой функция определена.
Пусть есть пересечение окрестностей и . Тогда на ней определены функции и . Причем .

Пусть есть произвольная последовательность, сходящаяся к , элементы которой принадлежат окрестности :
.
Тогда определены последовательности и . Причем последовательность является ограниченной снизу:
,
а последовательность является бесконечно большой:
.

Поскольку произведение бесконечно большой и ограниченной снизу последовательности является бесконечно большой последовательностью, то
.
Согласно определению предела последовательности по Гейне,
.

Теорема о частном от деления ограниченной функции на бесконечно большую

Все свойства ⇑ Если функция f ( x ) является бесконечно большой при x → x ₀ , а функция g ( x ) – ограничена на некоторой проколотой окрестности точки x ₀ , то
.

Для доказательства, мы воспользуемся определением предела функции по Гейне. Также используем свойство бесконечно больших последовательностей, согласно которому частное от деления ограниченной последовательности на бесконечно большую является бесконечно малой последовательностью.

Пусть функция является бесконечно большой при , а функция ограничена в некоторой проколотой окрестности точки :
при .

Поскольку функция бесконечно большая, то существует проколотая окрестность точки , на которой она определена и не обращается в нуль:
при .
Пусть есть пересечение окрестностей и . Тогда на ней определены функции и .

Поскольку частное от деления ограниченной последовательности на бесконечно большую является бесконечно малой последовательностью, то
.
Тогда, согласно определению предела последовательности по Гейне,
.

Теорема о частном от деления ограниченной снизу функции на бесконечно малую

Все свойства ⇑ Если функция , на некоторой проколотой окрестности точки , по абсолютной величине ограничена снизу положительным числом:
,
а функция является бесконечно малой при x → x ₀ :
,
и существует проколотая окрестность точки , на которой , то
.

Для доказательства этого свойства, мы воспользуемся определением предела функции по Гейне. Также используем свойство бесконечно больших последовательностей, согласно которому частное от деления ограниченной снизу последовательности на бесконечно малую является бесконечно большой последовательностью.

Пусть функция является бесконечно малой при , а функция ограничена по абсолютной величине снизу положительным числом, на некоторой проколотой окрестности точки :
при .

По условию существует проколотая окрестность точки , на которой функция определена и не обращается в нуль:
при .
Пусть есть пересечение окрестностей и . Тогда на ней определены функции и . Причем и .

Пусть есть произвольная последовательность, сходящаяся к , элементы которой принадлежат окрестности :
.
Тогда определены последовательности и . Причем последовательность является ограниченной снизу:
,
а последовательность является бесконечно малой с отличными от нуля членами:
, .

Поскольку частное от деления ограниченной снизу последовательности на бесконечно малую является бесконечно большой последовательностью, то
.
Согласно определению предела последовательности по Гейне,
.

Свойство неравенств бесконечно больших функций

Все свойства ⇑ Если функция является бесконечно большой при :
,
и функции и , на некоторой проколотой окрестности точки удовлетворяют неравенству:
,
то функция также бесконечно большая при :
.

Пусть функция является бесконечно большой при :
.
И пусть имеется проколотая окрестность точки , на которой
при .

Возьмем произвольную последовательность , сходящуюся к . Тогда, начиная с некоторого номера N , элементы последовательности будут принадлежать этой окрестности:
при .
Тогда
при .

Согласно определению предела функции по Гейне,
.
Тогда по свойству неравенств бесконечно больших последовательностей,
.
Поскольку последовательность произвольная, сходящаяся к , то по определению предела функции по Гейне,
.

Использованная литература:
Л.Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.

Читайте также: