Сформулируйте и докажите теорему о законах сложения векторов кратко

Обновлено: 30.06.2024

Вопрос по геометрии:

Сформулируйте и докажите теорему о законах сложения векторов

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок - бесплатно!

01.12.2016 19:19
Геометрия
remove_red_eye 17985
thumb_up 20

Ответы и объяснения 1

Теоремa:
Для любых векторов а,b,с справедливы равенства:
a+b=b+a(переместительный закон)
(a+b)+c=a+(b+c)(сочетательный закон)
Векторы а и b не коллинеарны.От произвольной точки А отложим векторы АВ=а и
АD=b и на этих векторах построим параллелограмм ABCD.По правилу треугольника AC=AD+DC=b+a.Аналогично AC=AD+DC=b+a.Дальше следует a+b=b+a.

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Геометрия.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи - смело задавайте вопросы!

Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.

Для того, чтобы ввести сумму векторов, сначала необходимо разобраться в таком понятии, как откладывание вектора от данной точки.

$\overrightarrow$ отложенный от точки $A$

Введем следующую теорему:

От любой точки $K$ можно отложить вектор $\overrightarrow$ и притом только один.

Доказательство.

Существование: Здесь нужно рассмотреть два случая:

В этом случае, очевидно, что искомый вектор -- вектор $\overrightarrow$.

Рисунок 2. Иллюстрация теоремы 1

Теорема доказана.

Сложение векторов. Правило треугольника

Пусть нам даны векторы $\overrightarrow$ и $\overrightarrow$.

Рисунок 3. Сумма векторов

Готовые работы на аналогичную тему

Иначе, определение 2, еще называют правилом треугольника для сложения двух векторов.

Из этого правила следует несколько свойств сложения двух векторов:

Для любого вектора $\overrightarrow$ выполняется равенство

Для любых произвольных точек $A,\ B\ и\ C$ выполняется равенство

Аналогично правилу треугольника можно строить сумму любого количества векторов. Такое правило сложения называется правилом многоугольника.

Правило параллелограмма

Помимо правила треугольника для сложения двух векторов, есть еще правило параллелограмма для сложения двух векторов. Сформулируем и докажем для начала следующую теорему.

Переместительный закон:

Сочетательный закон:

Доказательство.

Переместительный закон:

Рисунок 4. Иллюстрация переместительного закона

Тогда выполнение переместительно закона будет очевидно вытекать из равенства длин $\left|\overrightarrow+\overrightarrow\right|и\ |\overrightarrow+\overrightarrow|$.

Сочетательный закон:

Рисунок 5. Иллюстрация сочетательного закона

Из свойства правила треугольника $\overrightarrow+\overrightarrow=\overrightarrow$, получим:

Теорема доказана.

Пример задачи на сложение векторов

Дан четырехугольник $ABCD$. Доказать, что $\overrightarrow+\overrightarrow+\overrightarrow=\overrightarrow$

Доказательство.

Воспользуемся свойством правила треугольника $\overrightarrow+\overrightarrow=\overrightarrow$, получим:

В алгебре часто при упрощении выражений и различных вычислениях используются переместительный и сочетательный законы.

Эти законы также справедливы для векторов.

Вспомним правило сложения векторов – правило треугольника.

Пусть нам даны два вектора а и b.

От произвольно выбранной точки А отложим вектор АВ, равный вектору а.

Затем от точки В отложим вектор ВС, равный вектору b.

Вектор АС называется суммой векторов а и b.

Воспользуемся этим правилом треугольника для доказательства следующей теоремы.

Для любых векторов а , b и с справедливы равенства:

сумма векторов а и b равна сумме векторов b и а (переместительный закон);

сумма векторов а плюс b и с равна сумме векторов а и b плюс с (сочетательный закон).

Для доказательства переместительного закона рассмотрим случай, когда векторы а и b не коллинеарны, т.е. ненулевые и не лежат на одной или параллельных прямых (случай коллинеарных векторов рассмотрите самостоятельно).

От произвольной точки А отложим вектор АВ, равный вектору а, и вектор АD, равный вектору b.

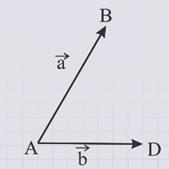
Основываясь на построенных векторах, достроим параллелограмм АВСD так, что вектор АВ равен вектору DС, а вектор АD равен вектору ВС.

По правилу треугольника сумма векторов АВ и ВС равна вектору АС, т.е. равна сумме векторов а и b.

С другой стороны, сумма векторов AD и DC также равна вектору АС, т.е. сумме векторов b и а.

Таким образом, сумма векторов а и b равна сумме векторов b и а.

Переместительный закон доказан.

Для доказательства сочетательного закона отложим от произвольной точки А вектор АВ, равный вектору а, от точки В вектор ВС, равный вектору b, и от точки С вектор CD, равный вектору с.

Рассмотрим сумму векторов а плюс b и вектора с с точки зрения правила треугольника: сумма векторов а и b равна вектору АС, в свою очередь, сумма вектора АС и вектора с равна вектору АD.

Теперь рассмотрим сумму векторов а и b плюс с: сумма векторов b и с, согласно рисунку, равна вектору ВD, в свою очередь, сумма векторов а и ВD равна вектору АD.

Исходя из этого, сумма векторов а плюс b и с равна сумме векторов а и b плюс с.

Что доказывает сочетательный закон.

Важно отметить, что при доказательстве переместительного закона было обосновано правило параллелограмма сложения неколлинеарных векторов: чтобы сложить неколлинеарные векторы а и b, необходимо от произвольной точки А отложить вектор АВ, равный вектору а, и вектор AD, равный вектору b, затем достроить параллелограмм АВСD, тогда вектор АС равен сумме векторов а и b.

Правило треугольника и правило параллелограмма находят сумму двух векторов, но как сложить несколько векторов?

Чтобы сложить несколько векторов, необходимо сложить первый вектор со вторым, затем сложить их сумму с третьим вектором и так далее.

Из законов сложения векторов следует, что сумма нескольких векторов не зависит от того, в каком порядке происходит сложение.

Рассмотрим рисунок, отражающий сумму векторов а, b и с:

от произвольной точки А отложен вектор АВ, равный вектору а, затем от точки В отложен вектор ВС, равный вектору b, и, наконец, от точки С отложен вектор CD, равный вектору с.

В результате получается вектор АD, равный сумме векторов а, b и с.

Если продолжить процесс откладывания векторов, можно построить сумму четырех, пяти, любого количества векторов.

Правило построения суммы нескольких векторов называется правилом многоугольника: если А1, А2, …,Аn – произвольные точки плоскости, то сумма векторов А1А2, А2А3, …, Аn –1An равна вектору А1Аn.

Это равенство справедливо для всех точек А1, А2, …, Аn, в частности, когда некоторые из них совпадают.

Важно заметить, что если начало первого вектора совпадает с концом последнего вектора, то сумма данных векторов равна нулевому вектору.

Итак, подведем итоги:

– Для любых векторов а, b и с справедливы равенства:

сумма векторов а и b равна сумме векторов b и а;

сумма векторов а плюс b и с равна сумме векторов а и b плюс с.

– Чтобы сложить неколлинеарные векторы а и b, необходимо от точки А отложить вектор АВ, равный вектору а, и вектор AD, равный вектору b, затем достроить параллелограмм АВСD, тогда вектор АС равен сумме векторов а и b (правило параллелограмма).

Здесь рассматриваем вектора на плоскости .

Основные определения

Вектором называется направленный отрезок , где точка – начало, точка – конец вектора.

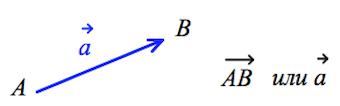
Нулевым вектором называется вектор, у которого начало совпадает с концом.

Векторы и называются одинаково направленными или сонаправленными , если лучи AB и CD одинаково направлены.

Если лучи AB и CD противоположно направлены, векторы и называются противоположно направленными .

Два вектора называются коллинеарными , если они лежат на одной прямой или на параллельных прямых.

Абсолютной величиной (или модулем) вектора называется длина отрезка, изображающего вектор. Абсолютную величину вектора обозначают .

Два вектора называются равными , если они одинаково направлены и равны по абсолютной величине.

Два вектора с равными модулями, лежащие на параллельных прямых, но противоположно направленные, называются противоположными . Вектор, противоположный вектору , обозначается как .

Сложение векторов

Сложение векторов и по правилу треугольника

Суммой двух векторов и называют такой третий вектор , начало которого совпадает с началом , а конец – с концом при условии, что конец вектора и начало вектора совпадают.

Сложение векторов и по правилу параллелограмма

Если два неколлинеарных вектора и привести к общему началу, то вектор совпадает с диагональю параллелограмма, построенного на векторах и . Причем начало вектора совпадает с началом заданных векторов.

Разностью векторов и называется вектор такой, что выполняется условие: .

Читайте также: