Процесс грама шмидта кратко

Реализация алгоритма

Данный скрипт, предназначенный для пакета Mathematica, проводит процесс ортогонализации Грама ― Шмидта над векторами, заданными в фигурных скобках предпоследний строки. Количество векторов и их координат могут быть произвольными. В данном случае для примера взяты вектора , ,

Свойства

he:תהליך גרם-שמידט hr:Gram-Schmidtov postupak is:Gram-Schmidt reikniritið sr:Грам-Шмитов поступак

Определение. Системы $S_ = \langle a_,a_,…,a_\rangle,$ и $S_ = \langle b_,b_,…,b_\rangle,$ называются эквивалентными, когда векторы каждой из систем, линейно выражаются через векторы, другой системы.

Теорема. Допустим, у нас есть линейно независимая система $S = \langle a_,a_,\ldots,a_\rangle.$ Тогда всегда найдется такая система $S_ = \langle b_,b_,…,b_\rangle,$ которая будет эквивалентной и ортогональной к $S,$ которая получается следующим методом:

1. $b_ = a_,$
2. $b_ = a_ + \sum\limits_^\lambda_b_,\: 2\leqslant j\leqslant k,$ при $\lambda_=-\dfrac<\left(a_, b_\right)><\left(b_, b_\right)>.$

Докажем же существование $S_$ эквивалентной $S$ с помощью индукции. При $k = 1$ $$b_ = a_.$$ При $k = 2$ $$\left(b_, b_\right) = \left(a_ + \lambda_b_, b_\right) = \left(a_, b_\right) + \lambda_\left(b_, b_\right) =$$$$= \left(a_, b_\right)-\dfrac<\left(a_, b_\right)><\left(b_, b_\right)>\left(b_, b_\right) = 0.$$ Из чего очевидно, что $S = \langle a_,a_\rangle$ и $S_ = \langle b_,b_\rangle$ — эквивалентны.

Теперь докажем для $k = m,$ при $2\leqslant j\leqslant k$ $$\left(b_, b_\right) = \left(a_ + \sum\limits_^\lambda_b_, b_\right) = \left(a_, b_\right) + \sum\limits_^\lambda_\left(b_, b_\right) =$$$$= \left(a_, b_\right)-\sum\limits_^\dfrac<\left(a_, b_\right)><\left(b_, b_\right)>\left(b_, b_\right) = 0.$$ Как видим, по индукции мы доказали, что любой ЛНЗ системе, методом Грама-Шмидта, можно найти эквивалентную ей ортогональную систему.

Примеры решения задач

Рассмотрим примеры задач, в которых может использоваться процесс ортогонализации Грама-Шмидта. Постарайтесь решить данные примеры самостоятельно, а затем сверить свое решение с приведенным.

Применяя процесс ортогонализации по Грамму-Шмидту построить ортогональный базис подпространства, натянутого на данную систему векторов $S = \langle a_, a_, a_\rangle.$
$$a_ = (1, 2, 2, -1), a_ = (1, 1, -5, 3), a_ = (3, 2, 8, -7).$$

Первым делом, найдем $b_$. В первом пункте пишется, что $b_ = a_.$

Дальше найдем $b_.$ Из формулы пункта 2), мы видим, что: $$b_ = a_ + \lambda_ \cdot b_, \lambda_ = \dfrac<\left(a_, b_\right)><\left(b_, b_\right)>,$$ все необходимое для решения мы нашли, осталось только решить. Итак:$$\lambda_ = -\dfrac<\left(a_, b_\right)><\left(b_, b_\right)> = -\dfrac<\left(1\cdot1 + 2\cdot1 + 2\cdot\left(-5\right) + 3\cdot\left(-1\right)\right)> <\left(1\cdot1 + 2\cdot2 + 2\cdot2 + \left(-1\cdot\left(-1\right)\right)\right)>= -\left(\dfrac\right) = 1,$$ лямбду мы нашли, $b_$ у нас есть, теперь мы можем найти $b_:$ $$b_ = a_ + \lambda_\cdot b_ = (1, 1, -5, 3) + (1, 2, 2, -1) = (2, 3, -3, 2).$$

Первым делом, найдем $b_$, $b_ = a_.$

Дальше найдем $b_.$ Из формулы пункта 2) мы видим, что: $$b_ = a_ + \lambda_ \cdot b_, \lambda_ = \dfrac<\left(a_, b_\right)><\left(b_, b_\right)>,$$ все необходимое для решения мы нашли, осталось только решить. Итак:$$\lambda_ = -\dfrac<\left(5\cdot1 + 8\cdot1 + \left(-2\cdot\left(-1\right)\right) + \left(-3\cdot\left(-2\right)\right)\right)> <\left(1\cdot1 + 1\cdot1 + \left(-1\cdot\left(-1\right)\right) + \left(-2\cdot\left(-2\right)\right)\right)>= -\left(\dfrac\right) = 3,$$ лямбду мы нашли, $b_$ у нас есть, теперь мы можем найти $b_:$ $$b_ = a_ + \lambda_\cdot b_ = (5, 8, -2, -3) + (-3, -3, 3, 6) = (2, 5, 1, 3).$$

Создатели алгоритма Эрхард Шмидт и Йорген Педерсен Грам.

Эрхард Шмидт (14 января 1876 — 6 декабря 1959) — немецкий математик, с 1917 года профессор Берлинского университета. В 1946—58 первый директор Института математики АН ГДР. Основные труды по теории функций, интегральным уравнениям, функциональному анализу. Определил и изучил геометрически гильбертово пространство, используя аналогии с геометрией Евклида. Занимался квадратичными формами. Известен оператор Гильберта-Шмидта и процесс Грама ― Шмидта.

Йорген Педерсен Грам (27 июня 1850 - 29 апреля 1916) датский математик, родился в герцогстве Шлезвиг, Дания и умер в Копенгагене, Дания. Основные его работы "On series expansions determined by the methods of least squares", "Investigations of the number of primes less than a given number". Математический метод, который носит его имя, процесс Грама-Шмидта, впервые был опубликован в 1883. Теорема Грама и Определитель Грама также назван в его честь.

1.2 Математическое описание алгоритма

1.2.1 Классический процесс Грама — Шмидта

1.2.1.1 Алгоритм

Пусть имеются линейно независимые векторы [math]\mathbf_1,\;\ldots,\;\mathbf_N[/math] .

Скалярное произведение для двух векторов [math]\mathbf< a= [a_1, a_2, . a_k]>[/math] и [math]\mathbf< b= [b_1, b_2, . b_k]>[/math] в k-мерном действительном пространстве определяется как:

Классический процесс Грама — Шмидта выполняется следующим образом:

На основе каждого вектора [math]\mathbf_j \;(j = 1 \ldots N)[/math] может быть получен нормированный вектор: [math]\mathbf_j = <\mathbf_j\over \| \mathbf_j \|>[/math] (у нормированного вектора направление будет таким же, как у исходного, а длина — единичной). Причем берется норма согласованная со скалярным произведением [math]\| x \| = \sqrt<\langle x, x \rangle>[/math]

Результаты процесса Грама — Шмидта:

[math]\mathbf_1,\;\ldots,\;\mathbf_N[/math] — система ортогональных векторов либо

[math]\mathbf_1,\;\ldots,\;\mathbf_N[/math] — система ортонормированных векторов.

Вычисление [math]\mathbf_1,\;\ldots,\;\mathbf_N[/math] носит название ортогонализации Грама — Шмидта, а [math]\mathbf_1,\;\ldots,\;\mathbf_N[/math] — ортонормализации Грама — Шмидта.

1.2.1.2 Доказательство

Докажем ортогональность векторов [math]\mathbf_1,\;\ldots,\;\mathbf_N[/math] .

Для этого вычислим скалярное произведение [math]\langle \mathbf_1, \mathbf_2 \rangle[/math] , подставив в него формулу (2). Мы получим ноль. Равенство нулю скалярного произведения векторов означает, что эти векторы ортогональны. Затем вычислим скалярное произведение [math]\langle \mathbf_1, \mathbf_3 \rangle[/math] , используя результат для [math]\langle \mathbf_1, \mathbf_2 \rangle[/math] и формулу (3). Мы снова получим ноль, то есть векторы [math]\mathbf_1[/math] и [math]\mathbf_3[/math] ортогональны. Общее доказательство выполняется методом математической индукции.

1.2.1.3 Геометрическая интерпретация — вариант 1

Рассмотрим формулу (2) — второй шаг алгоритма. Её геометрическое представление изображено на рис. 1:

Этот перпендикуляр — вычисляемый в формуле (2) вектор [math]\mathbf_2[/math] ;

3 — перемещение полученного на шаге 2 вектора [math]\mathbf_2[/math] в начало координат. Это перемещение сделано на рисунке лишь для наглядности. Оно не является математическим действием и поэтому не отражается в формуле (2).

На рисунке видно, что вектор [math]\mathbf_2[/math] ортогонален вектору [math]\mathbf_1[/math] , так как [math]\mathbf_2[/math] является перпендикуляром, по которому [math]\mathbf_2[/math] проецируется на [math]\mathbf_1[/math] .

Рассмотрим формулу (3) — третий шаг алгоритма — в следующем варианте:

Её геометрическое представление изображено на рис. 2:

5 — перемещение полученного [math]\mathbf_3[/math] в начало координат. Это перемещение сделано на рисунке лишь для наглядности. Оно не является математическим действием и поэтому не отражается в формуле (6).

На рисунке видно, что вектор [math]\mathbf_3[/math] ортогонален векторам [math]\mathbf_1[/math] и [math]\mathbf_2[/math] , так как [math]\mathbf_3[/math] является перпендикуляром, по которому [math]\mathbf_3[/math] проецируется на плоскость, образуемую векторами [math]\mathbf_1[/math] и [math]\mathbf_2[/math] .

1.2.1.4 Численная неустойчивость

При вычислении на ЭВМ по формулам (1) — (5) векторы [math]\mathbf_1,\;\ldots,\;\mathbf_[/math] часто не точно ортогональны из-за ошибок округления. Из-за потери ортогональности в процессе вычислений классический процесс Грама — Шмидта называют численно неустойчивым.

1.2.2 Модифицированный процесс Грама — Шмидта

1.3 Вычислительное ядро алгоритма

Вычислительное ядро последовательной версии метода ортогонализации Грамма-Шмидта можно составить из множественных (всего их [math]\frac[/math] ) вычислений проекций : [math]\mathbf_<\mathbf>\,\mathbf[/math]

1.4 Макроструктура алгоритма

Данный алгоритм использует в качестве составных частей другие алгоритмы. В дальнейшем имеет смысл описывать алгоритм не в максимально детализированном виде (т.е. на уровне арифметических операций), а давать только его макроструктуру, то есть описывает структуру и состав макроопераций. Типичной макрооперацией, часто встречающиеся в алгоритме является оператор проекции векторов. Как записано и в описании ядра алгоритма, основную часть метода ортогонализации Грамма-Шмидта составляют множественные (всего их [math]\frac[/math] ) вычисления оператора проекции.

1.5 Схема реализации последовательного алгоритма

Следующий алгоритм реализует нормализацию Грамма-Шмидта. Векторы [math]v_1. v_k[/math] заменяются набором ортонормированных векторов, которые имеют ту же линейную оболочку.

Вычислительная сложность этого [math]2Nk^2[/math] операции с плавающей точкой, где N - размерность векторов.

Последовательность исполнения метода следующая:

2. Далее для всех векторов [math]\mathbf _[/math] для [math]i=2 . N[/math] производим вычисление по следующей формуле: [math]<\mathbf >_=<\mathbf >_-\displaystyle \sum _>^><\mathbf >_<<<\mathbf >_>>\,<\mathbf >_[/math] .

1.6 Последовательная сложность алгоритма

Для построения ортогонального набора векторов в последовательном варианте требуется:

• [math]\frac[/math] делений,

• [math]\frac[/math] сложений (вычитаний),

• [math]\frac[/math] умножений.

• [math]\frac[/math] делений,

• [math]\frac[/math] сложений (вычитаний),

• [math]\frac[/math] умножений.

При классификации по последовательной сложности, таким образом, ортогонализация Грамма-Шмидта относится к алгоритмам с кубической сложностью.

1.7 Информационный граф

Опишем граф алгоритма как аналитически, так и в виде рисунка.

Граф алгоритма состоит из двух групп вершин, расположенных в целочисленных узлах двух областей.

Первая группа вершин расположена в двумерной области, соответствующая ей операция [math]\mathbf_<\mathbf>\,\mathbf = <\langle \mathbf, \mathbf \rangle \over \langle \mathbf, \mathbf\rangle> \mathbf ,[/math] .

Естественно введённые координаты области таковы:

i — меняется в диапазоне от 2 до N, принимая все целочисленные значения;

j — меняется в диапазоне от 1 до i-1, принимая все целочисленные значения.

Аргументы операции следующие:

[math]a_i[/math] : элементы входных данных, а именно [math]a_i[/math] ;

[math]b_j[/math] : результат срабатывания операции, соответствующей вершине из второй группы, с координатой j.

Вторая группа вершин расположена в двухмерной области, соответствующая ей операция [math]a - b[/math] .

Естественно введённые координаты области таковы:

i — меняется в диапазоне от 2 до N, принимая все целочисленные значения;

j — меняется в диапазоне от 1 до i-1, принимая все целочисленные значения.

Аргументы операции следующие:

j=1 - входные данные [math]a_j[/math]

j>1 - результат срабатывания операции, соответствующей вершине из второй группы, с координатой j-1

результат срабатывания операции, соответствующей вершине из первой группы, с координатой j

Рис. 5. Граф алгоритма с отображением входных и выходных данных. Proj - вычисление оператора проекции, F - операция a-b, In - входные данные, Out - результаты.

1.8 Ресурс параллелизма алгоритма

В параллельном варианте, в отличие от последовательного, вычисления [math]\mathbf_<\mathbf>\,\mathbf[/math] можно выполнять параллельно. То есть после каждого вычисления [math]b_j[/math] можно запускать параллельное вычисление [math]\mathbf_<\mathbf>\,\mathbf[/math] для всех [math]i=j+1..N[/math] . Кроме того можно параллельно производить вычитание соответствующего [math]\mathbf_<\mathbf>\,\mathbf[/math] для всех [math]i=j+1..N[/math] .

Для ортогонализации в параллельном варианте требуется последовательно выполнить следующие ярусы:

• [math]N[/math] ярусов в каждом из которых будет выполнятся,
• по [math]N - 1[/math] операторов проекций (в каждом из ярусов линейное количество проекций, в зависимости от яруса — от [math]N-1[/math] до [math]1[/math] ),
• по [math]N - 1[/math] сложений (в каждом из ярусов линейное количество сложений, в зависимости от яруса — от [math]N-1[/math] до [math]1[/math] ),

При классификации по высоте (количество ярусов в ЯПФ ) ЯПФ, таким образом, ортогонализация Грамма-Шмидта относится к алгоритмам со сложностью [math]O(N)[/math] .

При классификации по ширине (максимальное количество вершин в ярусе) ЯПФ его сложность будет [math]O(N^2)[/math] .

Объём входных данных: [math]Nk[/math]

Выходные данные: множество ортогональных векторов [math] _,\;\ldots ,\;\mathbf _> [/math] , каждый из которых описывается [math]\mathbf< b_i= [b^i_1, b^i_2, . b^i_k]>[/math] .

Объём выходных данных: [math]Nk[/math]

1.10 Свойства алгоритма

Соотношение последовательной и параллельной сложности в случае неограниченных ресурсов, как хорошо видно, является линейным (отношение кубической к квадратичной).

При этом вычислительная мощность алгоритма, как отношение числа операций к суммарному объему входных и выходных данных, также линейна.

Алгоритм почти полностью детерминирован — единственность результата выполнения гарантирована, однако возможно накопление ошибок округления при использовании классического процесса Грама-Шмидта. При этом модифицированный алгоритм дает более хороший результат.

Алгоритм является численно неустойчивым — ошибки округления могут привести к неортогональности полученных векторов.

Процесс Грама — Шмидта может применяться также к бесконечной последовательности линейно независимых векторов.

Процесс Грама ― Шмидта может быть истолкован как разложение невырожденной квадратной матрицы в произведение ортогональной (или унитарной матрицы в случае эрмитова пространства) и верхнетреугольной матрицы с положительными диагональными элементами ― QR-разложение, что есть частный случай разложения Ивасавы.

2 Программная реализация алгоритма

2.1 Особенности реализации последовательного алгоритма

2.2 Локальность данных и вычислений

2.3 Возможные способы и особенности параллельной реализации алгоритма

2.4 Масштабируемость алгоритма и его реализации

Проведём исследование масштабируемости параллельной реализации процесса ортогонализации Грама-Шмидта. Исследование проводилось на суперкомпьютере "Ломоносов" Суперкомпьютерного комплекса Московского университета. Исследовалась собственная параллельная реализация алгоритма, написанная на языке C++ с использованием стандарта MPI.

Версия MPI - intel opemmpi/1.8.4-icc

Модель используемого CPU - Intel Xeon X5570 2.93GHz

Набор и границы значений изменяемых реализации алгоритма:

• число процессоров [10:100] с шагом 10;
• размерность векторов [50 : 500] с шагом 50.

На следующем рисунке приведен график времени работы алгоритма в зависимости от числа процессов и размерности векторов.

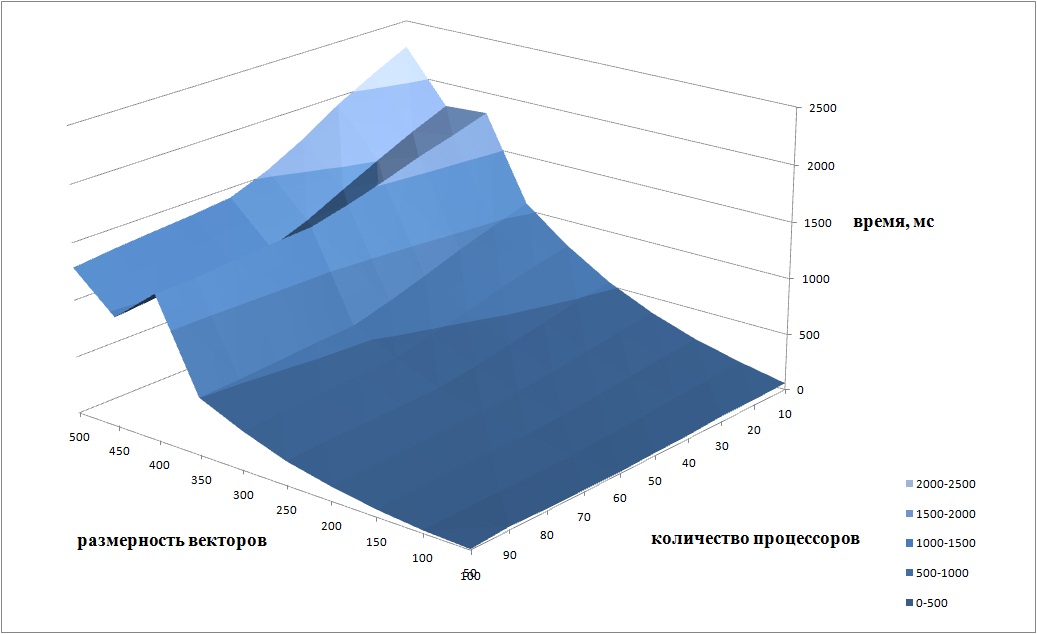
Так как алгоритм не поддается полному распараллеливанию, то при увеличении числа процессоров не происходит значительного ускорения. Это связано с тем, что параллельно можно вычислить лишь [math]b_j[/math] . То есть после каждого вычисления [math]b_j[/math] можно запускать параллельное вычисление [math]\mathbf_<\mathbf>\,\mathbf[/math] для всех [math]i=j+1..N[/math] . Кроме того можно параллельно производить вычитание соответствующего [math]\mathbf_<\mathbf>\,\mathbf[/math] для всех [math]i=j+1..N[/math] . Но после этого все процессоры должны синхронизоваться и дождаться когда получат следующий вектор [math]b_j[/math] .

Проведём еще одно исследование исследование масштабируемости параллельной реализации процесса ортогонализации Грама-Шмидта для меньшего числа процессоров. Исследование проводилось на суперкомпьютере "Ломоносов" Суперкомпьютерного комплекса Московского университета. Исследовалась параллельная реализация алгоритма, написанная с использованием стандарта MPI.

Набор и границы значений изменяемых реализации алгоритма:

• число процессоров [1:10] с шагом 1;
• размерность векторов [20 : 400] с шагом 20.

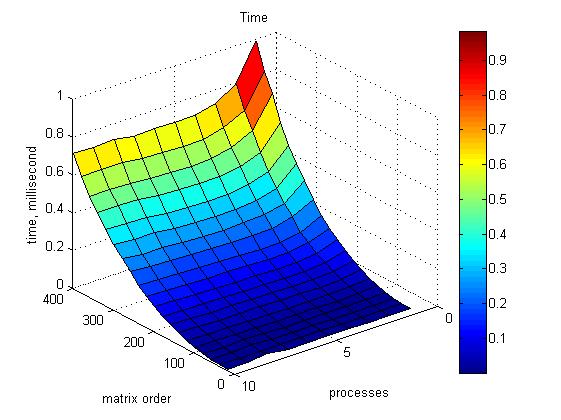
На графике 1 приведено время работы программы для разных значений размерности матрицы и числа процессоров.

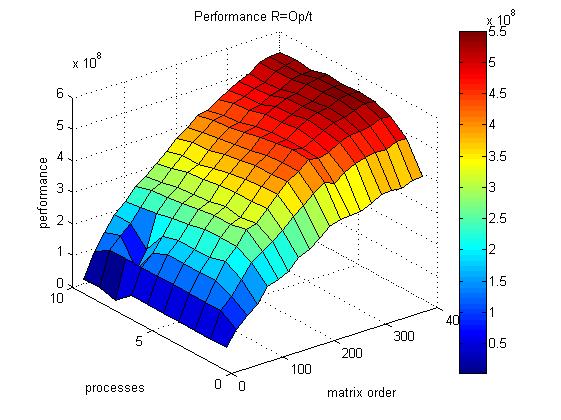
На графике 2 приведена производительность работы программы для разных значений размерности матрицы и числа процессоров.

На графике 3 приведена эффективность распараллеливания работы программы для разных значений размерности матрицы и числа процессоров.

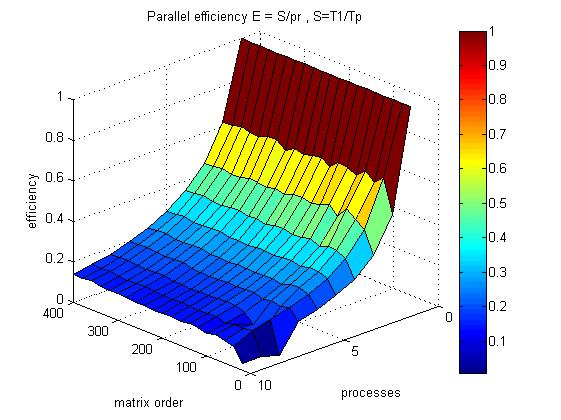
Оценим значения масштабируемости данной реализации: Общей оценкой масштабируемости по числу процессов будем называть среднее значение вклада каждого элемента рассматриваемой области значений в общую оценку по числу процессов по всем элементам рассматриваемой области параметров запуска.

• По числу процессоров: -0.009265. С увеличением числа процессоров наблюдается слабое снижение эффективности работы параллельной реализации алгоритма.

Общей оценкой масштабируемости по размеру решаемой задачи будем называть среднее значение вклада каждого элемента рассматриваемой области значений в общую оценку по размеру решаемой задачи по всем элементам рассматриваемой области параметров запуска.

• По размеру задачи: 0.00002555. При увеличении размерности задачи эффективность алгоритма очень медленно возрастает.

Общей оценкой масштабируемости будем называть средний размер вклада каждого элемента рассматриваемой области значений в общую оценку по всем элементам рассматриваемой области параметров запуска.

2.5 Динамические характеристики и эффективность реализации алгоритма

2.6 Выводы для классов архитектур

2.7 Существующие реализации алгоритма

Примеры библиотек, содержащих реализации алгоритма ортогонализации Грама-Шмидта:

2.7.1 Реализация для пакета Mathematica

Данный скрипт, предназначенный для пакета Mathematica, проводит процесс ортогонализации Грама ― Шмидта над векторами, заданными в фигурных скобках последней строки. Количество векторов и их координат могут быть произвольными. В данном случае для примера взяты векторы , , .

2.7.2 Реализация для Maxima

Данный скрипт, предназначенный для пакета Maxima, проводит процесс ортогонализации Грама ― Шмидта над векторами, заданными в квадратных скобках. Количество векторов и их координат могут быть произвольными.

В данном случае для примера взяты векторы [-2,1,0], [-2,0,1], [-0.5,-1,1].

2.7.3 Реализация для MATLAB

В MATLAB существует встроенная функция [Q,R]=qr(A) которая осуществляет ортогонализацию Грамма-Шмидта столбцов матрицы А. При этом столбцы матрицы предполагаются линейно независимыми.

[Q, R] = qr(A) возвращает матрицы Q с ортонормированными столбцами и обратимую верхнетреугольную матрицу R, так что A=Q*R

3 Литература

4 Ссылки

Навигация

Персональные инструменты

Пространства имён

Варианты

Просмотры

Поиск

Навигация

Хранилище файлов

Инструменты

Модифицированная ортогонализация Грама-Шмидта - известный алгоритм ортогонализации, который строит ортогональные векторы , линейная оболочка которых совпадает с линейной оболочкой .

Содержание

Введение

Рассмотрим ортогональное разложение , где - верхняя треугольная матрица размера × , - ортогональная × - матрица, . Для любой матрицы существует бесконечно много разложений указанного вида. Имея одно из них, легко выразить псевдообратную матрицу через и :

Для вычисления псевдообратной достаточно построить какое-нибудь ортогональное разложение матрицы , обратить верхнюю треугольную матрицу и умножить её на . Этот метод во многом удобнее явного обращения матрицы.

Метод ортогонализации Грама-Шмидта

Для построения разложения воспользуемся процессом ортогонализации Грама-Шмидта. Запишем матрицы и по столбцам:

Волной здесь и далее обозначается операция нормирования вектора:

Процесс ортогонализации Грама-Шмидта строит ортогональные векторы , линейная оболочка которых совпадает с линейной оболочкой :

Легко проверить, что для всех из , , векторы и ортогональны.

Вспомогательные утверждения

Лемма 1.1. На -м шаге процесса, , матрица представима в виде ортогонального разложения , где

- верхняя треугольная матрица,

По окончании процесса ортогонализации получаем ортогональное разложение .

С вычислительной точки зрения процесс Грама-Шмидта удобен тем, что на каждом шаге матрицы и получаются путём дописывания справа по одному столбцу к матрицам и соответственно. При этом предыдущие столбцы не изменяются (если не считать изменением дописывание нулей снизу к матрице - при разумной программной реализации эти нули всё равно не хранятся).

В следующей лемме утверждается, что обратная матрица также является верхней треугольной и формируется путём дописывания столбцов справа.

Лемма 1.2. Пусть матрицы невырождены и в блочной записи имеют вид

где - скаляр, - вектор-столбец размера . Тогда матрицы могут быть вычислены по рекуррентной формуле

где - скаляр, - вектор-столбец размера .

Замечание 1.1. Обеспечить невырожденность матрицы в процессе ортогонализации очень просто. Допустим, матрица невырождена. Поскольку - верхняя треугольная, вырожденность может возникнуть только в том случае, если . Такое возможно только при , а это означает, что вектор линейно зависит от векторов . Если в ходе процесса оказывается равным нулю, то коэффициент обнуляется и -й признак далее не учитывается, как будто его вообще не существовало. Если не равен, но близок к нулю, может возникнуть проблема неустойчивости решения, поскольку на приходится делить. На практике признак исключают, например, по такому условию: , где имеет порядок .

Назовём вектор текущим вектором коэффициентов на -м шаге. Этот вектор имеет размерность . По окончании процесса .

Лемма 1.3. Пусть выполняются условия предыдущей леммы. Тогда на -м шаге процесса вектор может быть вычислен по рекуррентной формуле

Назовём величину текущим значением функционала на -м шаге. Оно равно кратчайшему расстоянию от до линейной оболочки столбцов . По окончании процесса . Следующая лемма показывает, что текущее значение от шага к шагу только уменьшается.

Лемма 1.4. Значения могут быть вычислены в ходе ортогонализации по рекуррентной формуле

Лемма 1.5. Текущий вектор невязок на -м шаге процесса ортогонализации вычисляется по рекуррентной формуле

Алгоритм 1.1. Ортогонализация Грама-Шмидта

4: := ; (вычисление -й компоненты вектор-столбца );

5: := ; (ортогонализация относительно );

Модифицированная ортогонализация Грама-Шмидта

Если вместо := вычислять := , то формально результат не изменится, поскольку .

Данная модификация повышает численную устойчивость алгоритма. Это объясняется тем, что вектор обладает минимальной нормой среди всех векторов вида , где - произвольные коэффициенты. Поэтому при скалярном умножении на ошибки накапливаются существенно медленнее.

Прежде чем переходить к следующей модификации, запишем основную часть алгоритма ортогонализации, вычисляющую и .

Изменим порядок ортогонализации столбцов. До сих пор мы ортогонализовали столбец относительно предыдущих столбцов . Но можно сделать и подругому - ортогонализовать все последующие столбцы относительно :

Тогда в начале -го шага все столбцы по построению будут ортогональны всем столбцам . При этом подматрицы и вектор останутся такими же, как и до модификации.

Описанная модификация обладает важным преимуществом. Теперь на каждом шаге можно выбрать столбец , добавление которого наиболее выгодно. Чтобы не менять обозначений, будем полагать, что перед добавлением столбцы и переставляются местами (при реализации придётся сохранять соответствие между старой и новой нумерацией признаков, но мы не будем останавливаться на столь мелких технических деталях).

Возможны альтернативные критерии выбора добавляемого столбца:

1) столбец с максимальной нормой , что соответствует выбору столбца , максимально некоррелированного с ; применение этого критерия решает проблему вырожденности (см. Замечание 1.1); здесь существенно, чтобы матрица была заранее стандартизована;

3) столбец, добавление которого ведёт к наименьшему увеличению нормы вектора коэффициентов , что соответствует применению регуляризации;

4) столбец, после добавления которого значение функционала качества на независимой контрольной выборке окажется минимальным, что соответствует применению скользящего контроля (hold-out CV).

Алгоритм 1.2. Решение линейной задачи наименьших квадратов путём ортогонализации Грама-Шмидта с последовательным добавлением признаков

- параметр критерия останова.

- вектор коэффициентов линейной комбинации;

- минимальное значение функционала.

3: выбор по критериям и

4: перестановка местами столбцов:

6: вычисление текущего значения функционала:

7: обращение верхней треугольной матрицы :

8: вычисление текущего вектора коэффициентов:

10: прекратить добавление столбцов; выход;

12: := ; (компоненты вектор-столбца );

13: := ; (ортогонализация относительно );

16: конец цикла по .

Наконец, можно использовать совокупность критериев, выбирая тот столбец, добавление которого выгодно с нескольких точек зрения.

В Алгоритме 1.2 применяются первые два критерия.

Алгоритм состоит из основного цикла по , в котором поочерёдно добавляются столбцы. На шаге 3 принимается решение, какой из оставшихся столбцов добавить, затем он меняется местами со столбцом . Шаги 5–8 обновляют текущие значения функционала , обратной матрицы и коэффициентов . На шаге 9 проверяется условие останова: если достаточная точность аппроксимации уже достигнута, то добавлять оставшиеся столбцы не имеет смысла. Таким образом, Алгоритм 1.2 осуществляет отбор информативных признаков (features selection). Шаги 11–15 реализуют вложенный цикл, в котором все последующие столбцы ортогонализуются относительно только что добавленного столбца. Заодно обновляются значения квадратов норм столбцов и скалярных произведений , необходимые для эффективного выбора признака на шаге 3 в следующей итерации.

Читайте также:

  
• Требования к содержанию жилых помещений кратко
  
• Назовите и кратко охарактеризуйте основные типы учебных заведений функционировавших в древнем риме
  
• Сценарий нпк для начальной школы
  
• Условия выбора высоковольтных выключателей кратко
  
• Шлейермахер о разных методах перевода кратко