Парадокс процентов который активно пользуются политики и статистики на примере школьной задачи
Обновлено: 05.07.2024
Пользователи западного сегмента Twitter раскололись на два лагеря, пытаясь решить школьную задачу по математике, которую опубликовал микроблог pjmdoll. Проблема возникла вокруг спора о том, какое действие является приоритетным – умножение или деление, ведь в зависимости от этого результат уравнения радикально отличается.
В задаче требуется решить следующий пример: 8 ÷ 2 (2+2) = ? Однако одни комментаторы получили 16, другие — 1.
Это произошло из-за путаницы в приоритетах – одни отдали первенство умножению, другие - делению. При этом все раскрыли скобки правильно.
"Мой учитель математики учил, что умножение идет первым", — заявил один из пользователей. "Умножение и деление приоритетны над сложением и вычитанием, а между собой равнозначны. В какой последовательности они указаны в примере, так и решаются", — возразил другой пользователь.
По словам русскоязычных комментаторов, в США имеется стандарт PEMDAS, который определяет порядок вычисления. По этому правилу получается 1. Однако по российским правилам должно получаться 16.
Подписывайтесь на канал "Царьград" в Яндекс.Дзен
и первыми узнавайте о главных новостях и важнейших событиях дня.
Свидетельство и скидка на обучение каждому участнику
Зарегистрироваться 15–17 марта 2022 г.
Парадоксы в теории вероятностей и математической статистике
Теория вероятностей и математическая статистика — относительно молодые разделы современной математики, имеющие огромное прикладное значение почти во всех сферах деятельности человека.
Теория вероятностей — это строгая математическая дисциплина, занимающаяся поиском закономерностей случайных событий и изучающая их. Математическая статистика — это прикладная отрасль математики. Она занимается сбором исходной информации и обработкой ее в соответствии с законами теории вероятностей.
Объектом исследования теории вероятностей и математической статистики является случайное событие (явление) — такое, которое в результате испытания может произойти или не произойти. К числу случайных событий можно отнести появление дождя, который может идти или не идти, рождение ребенка мужского или женского пола, появление в данной местности какого-либо инфекционного заболевания, извержение вулкана, поражение мишени стрелком, количество повторений какой-либо буквы на печатной странице и т.д. и т.п. Во всех этих случаях под испытаниями мы понимаем те условия или обстоятельства, при которых рассматривается появление случайного события.
В течение долгого времени в науке исследовались детерминированные события. Это такого рода события, которые обязательно появляются в результате соблюдения определенных условий. Вероятностные события, таким образом, более широкий класс событий, которые в результате исходных условий, происходят или нет. Интерес к исследованию таких событий появился сравнительно недавно.
Эмпирическим, т.е. опытным путем было установлено, что появление в определенных испытаниях случайного события или его непоявление невозможно предвосхитить только тогда, когда проводится малое число испытаний. Если увеличить число испытаний, возможность появления случайного события можно предусмотреть.
В математической статистике есть много методов, нашедших широкое применение на практике. Их реализация апробирована многочисленными работами не только научного, но и практического характера.
После проведения контрольных наблюдений исследователь получает фактический материал, представляющий собой, как правило, большой объем числовых данных. Массив этих чисел труднообозрим, и сделать какие-то конкретные выводы непосредственно по ним невозможно. Здесь используются методы статистики, позволяющие провести классификацию первичных данных, представить их в наиболее наглядной форме и получить некоторые обобщающие показатели, которые дают возможность сравнивать между собой различные данные и делать определенные выводы.
В качестве обобщающих числовых показателей используются средние значения и характеристики варьирования (рассеивания) экспериментальных данных. Получив эти показатели для контрольной и экспериментальной групп, исследователь видит, что они различаются. Но возникает вопрос: насколько достоверны эти различия? Можно ли объяснить это различие действием предложенных нововведений или это различие – случайность, обусловленная малым объемом фактических данных и сильной вариативностью испытуемых? Здесь нужны методы проверки статистических гипотез.
Эти вопросы не исчерпывают круг задач, решаемых при конкретных исследованиях с использованием методов математической статистики. Конечно, большинство подобных задач решаются методами корреляционного и регрессионного анализа. Но вопрос о достоверности полученных результатов, все равно остается открытым…
Уточним: под случайным событием (возникновением специфического набора обстоятельств) подразумевается такое событие, которое в конкретном опыте может произойти или не произойти;
под случайной величиной – переменная, способная принимать любое значение из области определения, и с которой связано распределение вероятностей;
под вероятностью – действительное число в интервале от 0 до 1, относящееся к случайному событию и отражающее меру возможности его наступления или степень соответствующей уверенности.
Среди случайных событий выделяют:
а) практически достоверные, вероятность которых весьма близка к единице;
б) практически невозможные, если их вероятность близка к нулю;
в) независимые, когда появление одного из событий не изменяет вероятности возникновения других;
г) противоположные, если одно из них обязательно произойдет в каких-либо конкретных условиях;
д) совместные и несовместные, когда для первых возможно одновременное появление в каких-либо конкретных условиях, а для вторых это невозможно. Что касается случайных величин, то их принято делить на дискретные (способные принимать только отдельные значения) и непрерывные – с любыми значениями из конечного или бесконечного интервала.
Парадоксы – истины, противоречащие здравому смыслу
В теории вероятностей и математической статистике существует несколько задач, решение которых, на первый взгляд, противоречит здравому смыслу. Такие задачи называют парадоксами.
В теории вероятности и математической статистике парадоксы бывают двух типов:
первый – когда существует строгое решение в рамках аксиоматики, просто оно неочевидно, и условия задачи таковы, что ведут интуитивное понимание условий в ошибочном ключе, примерами таких парадоксов являются – Санкт-Петербургский парадокс, Парадокс закона больших чисел Бернулли, Парадокс дней рождения;
второй тип – парадоксы, которые основываются на неоднозначной интерпретации аксиоматики теории вероятности, её недоопределённости, которую отмечал еще Пуанкаре, их и можно назвать истинными парадоксами.
Примеры истинных парадоксов: Проблема Монти-Холла, Парадокс двух конвертов, Парадокс Хемпеля, Парадокс Бертрана. Ценность обоих типов парадоксов в том, что они помогают лучше понять суть теории, область её ограничения, глубже понять основания теории, и иногда исследование парадоксов вело к созданию отдельных разделов математики.
Теперь рассмотрим наиболее известные и интересные парадоксы.
Парадокс Монти Холла – одна из известных задач теории вероятностей, решение которой, на первый взгляд, противоречит здравому смыслу. Задача формулируется как описание игры, основанной на американском телешоу, и названа в честь ведущего этой передачи. Наиболее распространенная формулировка этой задачи, опубликованная в 1990 году, звучит следующим образом: представьте, что вы стали участником игры, в которой вам нужно выбрать одну из трех дверей. За одной из дверей находится автомобиль, за двумя другими дверями – козы. Вы выбираете одну из дверей, например, номер 1, после этого ведущий, который знает, где находится автомобиль, а где – козы, открывает одну из оставшихся дверей, например, номер 3, за которой находится коза. После этого он спрашивает вас, не желаете ли вы изменить свой выбор и выбрать дверь номер 2. Увеличатся ли ваши шансы выиграть автомобиль, если вы примете предложение ведущего и измените свой выбор?
После публикации немедленно выяснилось, что задача сформулирована некорректно: не все условия оговорены. Например, ведущий может придерживаться следующей стратегии: предлагать сменить выбор тогда и только тогда, когда игрок первым ходом выбрал автомобиль. Очевидно, что смена первоначального выбора будет вести в такой ситуации к гарантированному проигрышу. Наиболее популярной является задача с дополнительным условием – участнику игры заранее известны следующие правила: автомобиль равновероятно размещен за любой из 3 дверей; ведущий в любом случае обязан открыть дверь с козой и предложить игроку изменить выбор, но только не дверь, которую выбрал игрок; если у ведущего есть выбор, какую из 2 дверей открыть, он выбирает любую из них с одинаковой вероятностью.
У мистера Джонса двое детей. При этом старший ребёнок – девочка. Какова вероятность того, что оба ребёнка девочки?
У мистера Смита двое детей. При этом хотя бы один ребёнок – мальчик. Какова вероятность того, что оба ребёнка мальчики?
У мистера Джонса двое детей. При этом старший ребёнок – девочка. Какова вероятность того, что оба ребёнка девочки? Выберем случайную семью, соответствующую условиям первого вопроса. Тогда существуют 4 равновероятных исхода.
И только 2 из возможных исходов удовлетворяют критерию, указанному в вопросе. (Это варианты ДД, ДМ). Из-за того, что оба исхода из нового множества элементарных исходов равновероятны, и только один из исходов содержит 2-х девочек – ДД. Таким образом, вероятность того, что оба ребёнка девочки равна 1/2.
У мистера Смита двое детей. При этом хотя бы один из детей – мальчик. Какова вероятность того, что оба ребёнка мальчики? Второй вопрос похож на первый, однако вместо утверждения о том, что старший ребёнок мальчик, в вопросе говорится о том, что хотя бы один из детей мальчик. В ответ на критику со стороны читателей Гарднер соглашается, что из-за "невозможности детально описать процедуру рандомизации" его изначальная формулировка имеет 2 способа интерпретации метода отбора семьи:
1. Из всех семей с двумя детьми, где хотя бы один мальчик, выбрана произвольная семья. В этом случае ответ 1/3.
2. Из всех семей с двумя детьми, один ребёнок выбирается случайным образом, и пол этого ребёнка задан. В этом случае ответ 1/2.
Прекрасным примером служит парадокс с днями рождения. Выберем наугад 24 человека. Какова, по вашему мнению, вероятность того, что двое или большее число из них родились в один и тот же день одного и того же месяца (но, быть может, в разные годы)? Интуитивно чувствуется, что вероятность такого события должна быть очень мала. На самом же деле она оказывается равной 27/50, то есть чуть выше 50%!
Вероятность того, что дни рождения любых двух людей не совпадают, очевидно, равна 364/365. Вероятность несовпадения дня рождения третьего человека с днем рождения любых двух других членов отобранной группы составляет 363/365. Для четвертого человека вероятность того, что его день рождения отличается от дней рождения любых трех людей, равна 362/365 и т.д. Дойдя до двадцать четвертого участника эксперимента, мы увидим, что вероятность несовпадения его дня рождения с днями рождения остальных двадцати трех участников равна 342/365. Таким образом, мы получаем набор из 23 дробей. Перемножив их, мы найдем вероятность того, что все 24 дня рождения различны. Сократив числитель и знаменатель произведения двадцати четырех дробей, мы получим дробь 23/50. Иначе говоря, заключая пари на то, что среди 24, по крайней мере, двое родились в один и тот же день, вы будете выигрывать в 27 и проигрывать в 23 случаях из 50.
Санкт-Петербургский парадокс получил известность после публикации Даниилом Бернулли в заметках Академии наук Санкт-Петербурга в 1738 году, однако впервые парадокс упоминается двоюродным братом Даниила – Николаем Бернулли в 1713 году в письме к математику Монмору. Иногда, ошибочно, парадокс приписывают Эйлеру. Суть парадокса: игроком бросается правильная монета до момента выпадения решки, игрок при выпадении получает 2r рублей, где r – это номер бросания, при котором выпала решка, – при каждом последующем бросании потенциальный выигрыш увеличивается вдвое. Сколько необходимо выплатить игроку за участие в игре с такими условиями, чтобы его средний выигрыш перекрыл выплату за игру. Ответ парадоксален, – математическое ожидание банковских выплат бесконечное. Выигрыш может выпасть при любом из r бросаний, тогда математическое ожидание равняется:
где mx – математическое ожидание выигрыша, r – число бросаний.
Этот бесконечный ряд расходится, то есть имеет бесконечную сумму.
Парадокс двух конвертов – известный парадокс, демонстрирующий как особенности субъективного восприятия теории вероятностей, так и границы её применимости. В облике двух конвертов этот парадокс предстал в конце 1980-х годов, хотя в различных формулировках известен математикам с первой половины XX века. Есть два неразличимых конверта с деньгами. В одном находится сумма в два раза большая, чем во втором. Величина этой суммы неизвестна. Конверты дают двум игрокам. Каждый из них может открыть свой конверт и пересчитать в нём деньги. После этого игроки должны решить: стоит ли обменять свой конверт на чужой? Оба игрока рассуждают следующим образом. Я вижу в своём конверте сумму X. В чужом конверте равновероятно может находиться 2X или X/2. Поэтому, если я поменяю конверт, то у меня в среднем будет (2X+X/2)/2=(5/4)X, т.е. больше, чем сейчас. Значит – обмен выгоден. Однако обмен не может быть выгоден обоим игрокам. Где в их рассуждениях кроется ошибка?
Парадокс дней рождения. В группе, состоящей из 23 или более человек, вероятность совпадения дней рождения (число и месяц) хотя бы у двух людей превышает 50 % . Например, если к лассе 23 ученика или более, то более вероятно то, что у кого-то из одноклассников дни рождения придутся на один день, чем то, что у каждого будет свой неповторимый день рождения .
Для 60 и более человек вероятность такого совпадения превышает 99 %, хотя 100 % она достигает, согласно принципу Дирихле , только тогда, когда в группе не менее 367 человек (ровно на 1 больше, чем число дней в високосном году; с учётом високосных лет).
Такое утверждение может показаться неочевидным, так как вероятность совпадения дней рождения двух человек с любым днём в году (1/365 = 0.27 %), умноженная на число человек в группе (23), даёт лишь (1/365)×23 = 6.3 %. Это рассуждение неверно, так как число возможных пар (( 23 × 22 )/2 = 253) значительно превышает число человек в группе (253 > 23). Таким образом, утверждение не является парадоксом в строгом научном смысле: логического противоречия в нём нет, а парадокс заключается лишь в различиях между интуитивным восприятием ситуации человеком и результатами математического расчёта.
Как и любая другая область науки, теория вероятностей и математическая статистика отражает множество противоречий окружающего нас мира. В связи с этим в истории встречается множество различных парадоксов – истинных высказываний, для которых характерны неожиданность, непривычность, оригинальность, противоречивость себе, исходным посылкам, общепринятому, традиционному взгляду или здравому смыслу по содержанию и/или по форме.
По мнению Карла Пирсона, в математике нет другого такого раздела, где было бы столь же легко допустить ошибку, как в теории вероятностей. Разрешение же различных парадоксов, связанных со случайностью, способствовало возникновению и развитию теории вероятностей и её приложений. Величайшие открытия порой были результатом разрешения величайших парадоксов. Эти открытия, в свою очередь, становились источниками новых парадоксов. Из всех методов обучения метод, основанный на познании нового через парадоксы (метод Сократа), является фундаментальным, т.к. процесс научного познания сам опирается на парадоксы. Следовательно, анализ и пошаговый разбор парадоксов теории вероятностей и математической статистики ведет к более глубокому пониманию предмета и лучшему осознанию сути дела.
Список использованной литературы
1. Зайцев В. Ф. Математические модели в точных и гуманитарных нау- ках. – СПб.: ООО “Книжный Дом”, 2006. – 112 с.
2. Лубова, Т.Н. Многомерные статистические методы [Электронный ресурс]: учебное пособие / Т.Н. Лубова ; М-во сел. хоз-ва РФ, Башкирский ГАУ. – Уфа : Изд-во БГАУ, 2015. – 64 с.
3. Лубова, Т.Н. Теория вероятностей и математическая статистика [Электронный ресурс] : учебное пособие / Т. Н. Лубова ; М-во сел. хоз-ва РФ, Башкирский ГАУ. – Уфа : Изд-во БашГАУ, 2015. – 163 с.
4. Секей Г. Парадоксы в теории вероятностей и математической статистике: Пер. с англ. – М.: Мир, 1990. – 240 с.

В статье рассматриваются некоторые довольно неожиданные качественные эффекты, связанные с начислением процентов на проценты.
О логике и математике
Существуют разные взгляды на соотношение логики и математики. Некоторые серьезные мыслители рассматривают математику как часть логики. Существует и прямо противоположная точка зрения, согласно которой логика является частью математики. Логика – это система принципов, позволяющих делать верныe выводы на основе правильных посылок. Эти принципы были сформулированы еще Аристотелем и с тех пор не претерпели существенных изменений. Удивление может вызвать тот факт, что эти простые правила за столь длительное время не привели ни к одной ошибке.
Об экспоненциальном росте
После такого вступления уже можно рассмотреть логические и математические парадоксы, связанные с экспоненциальным ростом при начислении процентов на проценты.
Возьмем обычный газетный лист. Сложим его вдвое, потом еще вдвое и так далее. Попробуйте быстро оценить, какую толщину будет иметь газета, если мы проделаем эту операцию 50 раз? А теперь давайте посчитаем. После одной операции мы будем иметь два слоя бумаги, после двух – 4, после трех – 8…, после пятидесяти – 250. Если толщина газетного листа равна 0.1 миллиметра, то толщина пачки будет равна:
250/10=(210)5/10=10245/10>10005/10= =(105)3/10=1015/10=1014 миллиметров, или сто миллионов километров. Для сравнения: расстояние от Земли до Солнца равно примерно 150 миллионам километров.
Какое все это имеет отношение к финансовым рынкам? Да самое прямое! Мне несколько раз попадались компьютерные программы, авторы которых утверждали, что с их помощью можно на рынке FOREX зарабатывать порядка тысячи процентов годовых. Это значит, что капитал инвестора, пользующегося этой программой, каждый год увеличивается примерно в десять раз. Начав со скромной суммы в $10 тысяч, инвестор уже через два года станет миллионером, через пять – миллиардером, а еще лет через пять приберет к рукам все деньги на Земле. Остается непонятным, почему авторы программ сами не применят их на практике, а продают их за довольно скромные деньги? Из приведенных рассуждений видно, что доходность в тысячу процентов годовых слишком велика, и нельзя рассчитывать на стабильное получение такого дохода в течение достаточно долгого времени. Кстати, рассмотренный выше пример с газетой соответствует доходности в 100% годовых. Из приведенных оценок следует, что если речь идет о работе на рынке в течение 50 лет, то получить доходность в 100% годовых в принципе невозможно. Таким образом, если мы говорим о финансовых операциях с реинвестицией полученной прибыли, то с оценками доходности нужно быть достаточно осторожными.
Кое-какие характерные величины собраны в таблице 1. В ее первом столбце приведена дневная доходность, во втором та же доходность переведена в годовую, а в третьем она же пересчитана на срок в 50 лет. Из таблицы, в частности, видно, что для срока в 50 лет даже доходность 0.1% в день является запредельной!
Рассмотренные выше примеры говорят об одном: модели экспоненциального роста имеют весьма ограниченную область применимости. Например, газету еще никому не удавалось сложить вдвое десять раз. Физики хорошо знают, что экспонента – это модель взрыва. Еще один классический пример того, как в моделях экспоненциального роста не учитываются границы их применимости, дает теория Мальтуса.
Гарантированные выигрыши
Хорошо известен следующий способ получить гарантированный выигрыш при игре в орлянку. Поставим на кон 1 рубль. Если в первой же игре мы выиграем, то игру сразу же прекратим. В противном случае удвоим ставку и сыграем еще раз. В случае выигрыша прекратим игру, а иначе вновь удвоим ставку – и так далее. Вероятность проиграть в первой игре равна 0.5. Вероятность проиграть два раза подряд равна 1/4, три раза подряд – 1/8, вероятность проиграть n раз подряд равна 2-n. Видим, что эта вероятность экспоненциально быстро убывает, поэтому с вероятностью единица игра закончится на каком-то шаге. Подсчитаем прибыли и убытки в случае, если это произошло в игре с номером n.
В первой игре мы проиграли рубль, во второй – два, в (n-1)-ной 2n-2 рублей, а в последней – выиграли 2n-1 рублей. Итог всей операции – один рубль выигрыша*. Результат явно парадоксальный. Корень парадокса заключается в экспоненциальном росте размера ставок. Разобранный выше пример с газетой свидетельствует о том, что уже на пятидесятую ставку никаких денег не хватит. У реального игрока проблемы начнутся гораздо раньше.
Описанный эффект имеет чисто качественный характер и относится отнюдь не только к игре орел-решка.
Допустим, мы работаем на финансовом рынке и имеем какой-то инструмент, выдающий сигналы на вход в рынок. Установим стоп-ордера так, чтобы в случае удачи получать f рублей на вложенный рубль, а в случае неудачи фиксировать убыток в g рублей на вложенный рубль. Можно предположить, что результат такой операции – случайное событие, и с вероятностью p мы получим прибыль, а с вероятностью q=1-p зафиксируем убыток.
Допустим, мы хотим заработать сумму M (миллион). Откроем первую позицию в размере M/f. Если операция закончится с прибылью, то задача решена. В противном случае продолжим игру, вложив сумму M(1+g)/f и так далее. Вероятность проиграть n раз подряд, очевидно, равна qn и быстро стремится к нулю с ростом n. Поэтому с вероятностью единица мы рано или поздно выиграем и заработаем свой миллион.
Все сказанное носит чисто качественный характер: результат не зависит ни от наших амбиций, ни от размеров прибыли и убытка, ни даже от вероятности выигрыша. Важно лишь, чтобы вероятность выигрыша была ненулевой. Правда, и размер инвестируемых средств будет экспоненциально расти независимо от всех этих параметров. Поэтому и объяснение парадокса имеет чисто качественный характер.
Петербургский парадокс
Еще один парадокс такого рода был предложен в 1713 году Николаем Бернулли. По месту публикации он носит название петербургского парадокса. Рассмотрим следующую ситуацию. Петр и Павел уговариваются сыграть ряд партий в орла или решку. Если Петр выигрывает первую партию, Павел платит ему 2 рубля, и игра прекращается. Если Петр проигрывает первую партию и выигрывает вторую, Павел выплачивает ему 4 рубля, и игра заканчивается… Если Петр проигрывает подряд n-1 партий, а затем выигрывает n-ную, Павел выплачивает ему 2n рублей, и игра прекращается. Спрашивается, какова справедливая плата за участие в такой игре? Вероятность получить выигрыш в размере 2n, очевидно, равна 1/2n. События эти независимы, поэтому математическое ожидание выигрыша Петра равно: 2(1/2)+4(1/4)+…+2n(1/2n)+… = = 1+1+…, то есть равно бесконечности.
Таким образом, сколько бы ни заплатил Петр в начале игры, в конце концов он, вероятно, окажется в выигрыше. А между тем никакой здравомыслящий человек на месте Петра не согласился бы поставить и ста рублей против обязательств Павла.
Этот парадокс достаточно долго занимал математиков. Была даже разработана альтернативная теории вероятностей теория морального ожидания. А ларчик открывался просто. Объяснение было дано, насколько я понимаю, Эмилем Борелем [1] в первой половине прошлого века.
Объяснение парадокса опять связано с экспоненциальным ростом ставок. Давайте представим, что Павел продает свои обязательства по частям. Плата в один рубль за право с вероятностью 1/2 получить два рубля и с вероятностью 1/2 не получить ничего – вполне справедлива, и, вероятно, Павел найдет покупателя. То же относится и к обязательству выплатить 4 рубля с вероятностью 1/4 и ничего не платить с вероятностью 3/4. А вот продать за рубль право получить 250 рублей или не получить ничего – Павлу вряд ли удастся, ибо каждый нормальный человек сообразит, что таких денег у Павла нет.
Если учесть это обстоятельство, можно сказать, что справедливая плата за участие в игре никак не больше 50 рублей. Кстати, этот пример можно перевести на язык опционов, поэтому он не так уж далек от реальной жизни. А выводы, как и в предыдущем примере, носят качественный характер.
Разобранные примеры показывают, что если в математической модели явно или неявно появляется экспоненциальный рост, то нужно очень внимательно отслеживать границы применимости модели.
Реинвестиции прибыли
Пусть имеются два способа вложения денег. При способе А мы будем каждый год стабильно получать прибыль в f рублей на вложенный изначально рубль. При способе Б мы будем получать в год прибыль в g рублей на вложенный рубль, но с возможностью многократной реинвестиции полученной прибыли. Какой способ предпочесть?
Давайте посчитаем. Каждый вложенный рубль при способе Б через n лет превратится в сумму (1+g)n. Прибыль за n-ный год при этом составит:
(1+g)n-(1+g)n-1=g(1+g)n-1.
Видно, что получаемая прибыль год от года растет, причем скорость роста прибыли g(1+g)n-1-g(1+g)n-2=g2(1+g)n-2 не меньше g2. Поэтому не позднее, чем через T=2f/g2 лет прибыль при способе Б будет вдвое превышать прибыль, получаемую при способе А. Значит уже через 2T лет суммарная прибыль от вложений при способе Б превысит суммарную прибыль от вложений способом А**. Таким образом, если у нас в запасе достаточно много времени, то способ Б определенно предпочтительнее. И это – независимо от соотношения ставок f и g! Кстати, этот вывод останется верным и в том случае, когда периодичности получения прибыли при этих двух способах не совпадают. Более того, он не зависит и от частоты получения прибыли, лишь бы эта частота при способе Б была положительной.
Напрашивается вывод о том, что способ Б лучше. Но, с другой стороны, если мы вкладываем деньги всего на год, а f>g, то при способе А мы заработаем больше. Поэтому правильный вывод выглядит следующим образом. Если f>g, то все зависит от срока инвестиций: если он меньше некоторого порогового значения – предпочтительнее способ А, а в противном случае – способ Б.
Здесь xt и yt – остаток на счете в году t в первом и во втором случаях, а x0=y0 – начальная сумма инвестиций. Первая формула задает хорошо знакомую со школы геометрическую прогрессию, поэтому сразу можно сказать, что xt=x0+(x0 f-m)(t-1). Со второй нужно немножко повозиться. Если мы инвестируем сумму m/g, то полученной прибыли в конце года как раз хватит на необходимые выплаты. Если есть возможность инвестировать больше, то условно разделим всю сумму на две части: первая в размере m/g будет использоваться для поддержания деятельности, а остаток будет реинвестироваться вместе с прибылью. Поэтому yt=m/g+(y0-m/g)(1+g)t-1. В последней формуле мы видим все ту же экспоненту, поэтому можем сделать вывод, что при достаточно большой начальной сумме и при достаточно большом сроке инвестиций способ Б лучше, независимо от ставок f и g. Но появляется и новый качественный эффект (рис. 1).
Рис. 1. Динамика счета при различных начальных условиях.
При некоторых соотношениях между объемом начального капитала, размером необходимых затрат и доходностью операций может случиться так, что способ А дает возможность сколь угодно долго жить безбедно, а способ Б неизбежно приводит к разорению***. Заметим, кстати, что если есть возможность комбинировать эти два способа, то при больших сроках инвестиции оптимальным становится портфель, соответствующий вложению суммы m/f по способу А и остальных денег – по способу Б (несложные выкладки оставляем читателю).
Фактор времени
* Как это следует из знакомой со школы формулы суммы членов геометрической прогрессии.
** Здесь нас интересует лишь качественный эффект, поэтому я ограничиваюсь весьма грубыми оценками. При желании в этой задаче такие оценки легко могут быть уточнены.
*** Можно было бы учесть и издержки, пропорциональные обороту (комиссионные, налоги на прибыль и т. п.). Однако к новым качественным эффектам это не приводит, поскольку легко сводится просто к уменьшению ставок f и g.
2002
Михаил Горелов
Литература:
1. Борель Э. Вероятность и достоверность. – М.: ГИФМЛ, 1961.
2. Винс Р. Математика управления капиталом. – М.: Альпина Паблишер, 2001.
Понравился пост? Подпишись на обновления сайта по s RSS, Email или twitter!

В повседневной жизни мы постоянно сталкиваемся с ситуациями неопределенности. Так, по крайней мере подсознательно, мы постоянно встречаемся с вероятностями. Более того, нам кажется, что у нас хорошо развито интуитивное чувство вероятности. Но так ли это на самом деле?
Мы знаем, что, если подбросить монетку 100 раз, то она упадет около 50 раз решкой вверх и 50 раз вверх орлом. Также понятное дело, что вероятность наткнуться на друга в отпуске за границей очень невысокая, хотя и не равно нулю. Однако существуют ситуации, в которых верные предсказания в соответствии с теорией вероятности совершенно не согласуются с теми, которые подсказывает интуиция.
Давайте погрузимся в пять парадоксов теории вероятности и статистики, которые предлагают абсурдные на вид результаты. Тем не менее они достоверны.
1. Парадокс дней рождения
Вы на вечеринке у друга, на которой присутствует 30 человек. Какова вероятность, что у двух из них день рождения будет в один и тот же день? Что подсказывает вам интуиция? Возможно, что какая-то вероятность имеется, однако она очень низкая?
Итак, условие парадокса дней рождения звучит следующим образом:
Сколько людей должно быть на вечеринке, чтобы вероятность того, что у двоих из них дни рождения будут в один день, составляла как минимум 50 процентов?
Парадокс предполагает, что вероятность того, что каждый из дней в году в равной степени будет днем рождения случайного человека.
Ответ поражает: всего 23! На вечеринки у вашего друга, на которой присутствует 30 человек, вероятность того, что у двух человек будут дни рождения в один день, составляет более 70%!
2. Парадокс Симпсона
Предположим, что мы бизнес-партнеры. У нас есть пять разных кофеен по всему городу. В качестве маркетинговой стратегии мы выдаем ваучеры самым лояльным клиентам в надежде на то, что они вернутся и купят еще больше кофе.
Однако возникает спор о том, каким должен быть номинал ваучеров. Чтобы прийти к наилучшему решению, мы выдаем ваучеры с разными номиналами. Мы собираем данные о том, сколько прибыли получили с каждого лояльного клиента в течение следующего месяца.
После одного месяца все кажется понятным: для каждой из пяти наших кофеен тенденция одинаковая. Чем больше номинал ваучера, тем больше прибыли мы получили от соответствующего покупателя.
Однако при общем рассмотрении данных из пяти кофеен вместе наблюдается прямо противоположная тенденция: чем больший номинал у ваучера, тем меньше прибыли принес клиент. Как такое может быть?
Это и есть Парадокс Симпсона:
Тенденция, наблюдаемая в разных группах, может пропасть при объединении данных.
3. Парадокс коробок Бертрана
Если вы знакомы с парадоксом Монти Холла, то этот парадокс очень на него похож. Напротив нас стоят три коробки:

В одной коробке лежат две серебряные монеты, во второй — две золотые, а в третьей — одна золотая и одна серебряная. Мы не знаем, в какой коробке какие монеты. Итак, выбираем случайную коробку и вслепую достаем одну монету из этой коробки.Она золотая!
Какова вероятность того, что вторая монета в выбранной нами коробке также золотая?
Наивным (и неверным) предположением многих людей при первом столкновении с этой задачей будет вероятность в ½. Что-то подсказывает: если мы вытянули золотую монету, то эта коробка содержит либо 2 золотые, либо одну золотую и одну серебряную монету. В первом случае мы бы вытянули другую золотую монету, а во втором — нет. Таким образом можно предположить, что вероятность составляет ½.
Однако реальная вероятность — ⅔.
Причина этому — первая вытянутая золотая монета могла быть либо единственной золотой монетой в ящике с одной золотой и одной серебряной монетой, первой золотой монетой в ящике с золотыми монетами либо второй золотой монетой в ящике с золотыми монетами. И в двух из этих вариантов мы вытянем золотую монету:
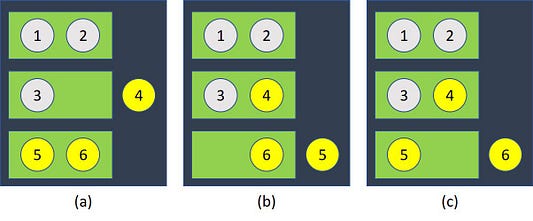
4. Парадокс пари (Парадокс галстуков)
После новогодних праздников вы возвращаетесь в офис в новом галстуке, который получили в подарок. Вашему коллеге Бобу также подарили на Новый год галстук. Никто из вас не знает цены своего галстука. Вы начинаете спорить насчет того, у кого галстук дороже.
Боб и вы заключаете пари: каждому из вас необходимо узнать цену своего галстука. Тот, чей галстук дороже, должен будет отдать его тому, чей галстук дешевле.

Боб думает, что спор в любом случае разрешится в его пользу:Его шансы выиграть или проиграть — 50/50. Если он проиграет, то он потеряет стоимость своего галстука. Если он победит, то выиграет больше, чем стоит его галстук.
Но со своей точки зрения вы можете построить такую же логическую цепочку и прийти к заключению, что спор будет в вашу пользу.
Но пари не может быть одновременно в вашу пользу и в пользу Боба. Так где же ошибка?
Чтобы решить Парадокс галстуков нужно включить цены галстуков в расчеты:пусть один галстук стоит 1000 рублей, а другой — 500 рублей. Если выиграет Боб, то его выигрыш составит галстук стоимостью 1000 рублей. Если он проиграет, это будет значить, что у него был более дорогой галстук, и он только что потерял 1000 рублей. Таким образом, потенциальный выигрыш отменяется, и такой спор по сути невыгоден никому.
5. Случайное блуждание
Этот факт не считается парадоксом, но он кажется таким захватывающим и удивительным, что должен быть в этом списке.
Представьте муравья на бесконечном листе бумаги. Каждую секунду муравей случайным образом направляется в одном из четырех возможных направлений (вперед, назад, влево или вправо). Вероятности, что он пойдет в каждом из этих направлений, равны. Этот сценарий называется случайной симметричной 2D-прогулкой, так как бумага двумерная.
Также можно представить, что муравей ползет не по листу бумаги, а по нитке. В этом случае муравей может двигаться лишь вперед и назад, и мы знакомимся со случайной 1D-прогулкой.
Таким же образом можно представить случайную 3D-прогулку,где путешественник — это дрон или птица, которая случайным образом двигается в шести направлениях (вперед/назад, влево/вправо, вверх/вниз).
Какова вероятность, что путешественник вернется в начальное положение?
Ответ удивляет: для муравья на нитке (1D) или на бумаге (2D) вероятность равна 1. Однако для птицы существует вероятность, что она улетит в бесконечное путешествие безвозвратно. Это утверждение также будет верно для 4, 5, 6-мерного мира.
Такие математические выводы ошеломляют. Можно смотреть на математическую логику, но очень сложно до конца понять ее на интуитивном уровне. Математик Сидзуо Какутани с улыбкой сказал по этому поводу:
Пьяный человек найдет дорогу домой, но пьяная птица может потеряться навсегда.
Читайте также:

