Основные понятия математической статистики кратко
Обновлено: 05.07.2024
Окружающий нас мир насыщен информацией – разнообразные потоки данных окружают нас, захватывая в поле своего действия, лишая правильного восприятия действительности. Не будет преувеличением сказать, что информация становится частью действительности и нашего сознания.
Без адекватных технологий анализа информации (данных) человек оказывается беспомощным в жестокой информационной среде. Статистика позволяет компактно описать данные, понять их структуру, провести классификацию, увидеть закономерности в хаосе случайных явлений.
Для студентов, магистрантов, аспирантов и соискателей полезно и необходимо знать, где, когда и как методы математической статистики могут применяться на практике для анализа данных психолого-педагогического исследования. Поэтому необходимо развить интуитивное и практическое представление об анализе данных, статистической обработке педагогического эксперимента, не предполагая наличия у них специальной подготовки. От педагога-исследователя требуются сейчас хорошие знания информатики, основных статистических методов, а также умение ставить и решать исследовательские задачи с использованием ЭВМ.
Приведем несколько примеров применения методов анализа данных в практических задачах.
Пример 1. Рассмотрим довольно часто встречающуюся задачу. Предположим, что Вы изобрели важное нововведение: изменили систему оплаты труда, перешли на выпуск новой продукции, использовали новую технологию, методику. Вам кажется, что это дало положительный эффект, но действительно ли это так? А может быть этот кажущийся эффект определен вовсе не вашим нововведением, а естественной случайностью, и уже завтра Вы можете получить прямо противоположный, но столь же случайный эффект? Для решения этой задачи надо сформировать два набора чисел, каждый из которых содержит значения интересующего вас показателя эффективности до и после нововведения. Статистические критерии сравнения двух выборок покажут Вам, случайны или неслучайны различия этих двух рядов чисел.
Пример 2. Другая важная задача состоит в прогнозировании будущего поведения некоторого временного ряда: изменения курса доллара, цен и спроса на продукцию или сырье. Для такого временного ряда с помощью статистических методов подбирают некоторое аналитическое уравнение – строят регрессионную модель. Если мы предполагаем, что на интересующий нас показатель влияют некоторые другие факторы, их тоже можно включить в модель, предварительно проверив значимость этого влияния. Затем на основе построенной модели можно сделать прогноз и указать его точность.
Пример 4. Пусть у вас имеются данные о минеральной воде, поступившей из различных источников: энергетическая ценность, состав, цвет, содержание других веществ, стоимость доставки. И вы хотите определить наиболее ценную по свойствам и более дешевую по себестоимости минеральную воду. Решить данную задачу можно также с помощью методов математической статистики (кластерный анализ).
Все приведенные примеры имеют одну общую черту: непредсказуемость результатов для действий, которые проводятся в неизменных условиях. Еще одной особенностью приведенных примеров является сравнительно малый объем исходных данных (объем выборки). Причина этого состоит в том, что для большинства прикладных исследований, особенно в гуманитарных областях, характерны именно небольшие объемы данных (исключение здесь составляет лишь демография и отдельные области медицинской статистики).
Математическая статистика – раздел математики, посвященный математическим методам систематизации, обработки и использования статистических данных для научных и практических выводов. Определение, сформулированное видными отечественными математиками Андреем Николаевичем Колмогоровым и Юрием Васильевичем Прохоровым.
Математическая статистика исходит из предположения, что наблюдаемая изменчивость окружающего мира имеет два источника:
– действие известных причин и факторов. Они порождают изменчивость, закономерно объяснимую.
Проверка психолого-педагогических гипотез и моделей является тоже случайным событием, так как результаты педагогического исследования определяются очень большим количеством заранее непредсказуемых факторов. Определенные закономерности можно выявить только в случае массовых наблюдений вследствие закона больших чисел. Закон больших чисел – это объективный математический закон, согласно которому совместное действие большого числа случайных факторов приводит к результату, почти не зависящему от случая.
Отсюда совершенно очевидным является факт, что педагогические измерения однозначно связаны со статистическими измерениями.
Статистический подход – это выявление закономерной изменчивости на фоне случайных факторов и причин. Методы математической статистики позволяют оценить параметры имеющихся закономерностей, проверить те или иные гипотезы об этих закономерностях.
Аппарат математической статистики является изумительным по мощности и гибкости инструментом для отсеивания закономерностей от случайностей. Педагогу-исследователю обязательно необходимо накапливать информацию об окружающем мире, пытаясь выделить закономерности из случайностей.
Математическая статистика возникла (XVII в.) и развивалась параллельно с теорией вероятностей. Дальнейшее развитие математической статистики (вторая половина XIX — начало XX в.) обязано, в первую очередь, Пафнутию Львовичу Чебышеву, Андрею Андреевичу Маркову, Александру Михайловичу Ляпунову, а также Карлу Гауссу, Адольфу Кетле, Френсису Гальтону, Карлу Пирсону и др.
В XX в. наиболее существенный вклад в математическую статистику был сделан советскими математиками (Всеволод Иванович Романовский, Евгений Евгеньевич Слуцкий, Андрей Николаевич Колмогоров, Н. В. Смирнов), а также английскими (Стьюдент (Уильям Госсет), Роберт Фишер, Эдмилсон Пирсон) и американскими (Ю. Нейман, Абрахам Вальд) учеными.
Исходным понятием статистики является понятие совокупность, объединяющее обычно какое-либо множество испытуемых (учащихся) по одному или нескольким интересующим признакам. Главное требование к выделению изучаемой совокупности — это ее качественная однородность, например, по уровню знаний, росту, весу и другим признакам. Члены совокупности могут сравниваться между собой в отношении только того качества, которое становится предметом исследования. При этом обычно абстрагируются от других неинтересующих качеств. Так, если педагога интересует успеваемость учащихся, то он не принимает во внимание, как правило, их рост, вес и другие параметры, не относящиеся непосредственно к изучаемому вопросу.
Применение большинства статистических методов основано на идее использования небольшой случайной совокупности испытуемых из общего числа тех, на которых можно было бы распространить (генерализовать) выводы, полученные в результате изучения совокупности. Эта небольшая совокупность в статистике называется выборочной совокупностью (или короче — выборкой). Главный принцип формирования выборки — это случайный отбор испытуемых из мыслимого множества учащихся, называемого генеральной совокупностью или популяцией объектов или явлений. Как по анализу элементов, содержащихся в капле крови, медики нередко судят о составе всей крови человека, так и по выборочной совокупности учащихся изучаются явления, характерные для всей генеральной совокупности.
Когда для каждого объекта в выборке измерено значение одной переменной, популяция и выборка называются одномерными. Если же для каждого объекта регистрируются значения двух или нескольких переменных, такие данные называются многомерными.
Одной из основных задач статистического анализа является получение по имеющейся выборке достоверных сведений об интересующих исследователя характеристиках генеральной совокупности. Поэтому важным требованием к выборке является ее репрезентативность, то есть правильная представимость в ней пропорций генеральной совокупности. Достижению репрезентативности может способствовать такая организация эксперимента, при которой элементы выборки извлекаются из генеральной совокупности случайным образом.
Обычно в статистике различают три типа значений переменных: количественные, номинальные и ранговые.
Значения количественных переменных являются числовыми, могут быть упорядочены и для них имеют смысл различные вычисления (например, среднее значение). На обработку количественных переменных ориентировано подавляющее большинство статистических методов.
Значения номинальных переменных (например: пол, вид, цвет) являются нечисловыми, они означают принадлежность к некоторым классам и не могут быть упорядочены или непосредственно использованы в вычислениях. Для анализа номинальных переменных специально предназначены лишь избранные разделы математической статистики, например, категориальный анализ. Однако в ряде случаев для этой цели могут быть использованы и некоторые ранговые и количественные методы, если номинальные значения предварительно заменить на числа, обозначающие их условные коды.
Ранговые или порядковые переменные занимают промежуточное положение: их значения упорядочены (состояние больного, степень предпочтения), но не могут быть с уверенностью измерены и сопоставлены количественно. К анализу ранговых переменных применимы так называемые ранговые методы.
Ранг наблюдения – это тот номер, который получит данное наблюдение в упорядоченной совокупности всех данных – после их упорядочивания по определенному правилу (например, от большего значения к меньшим). Процедура перехода от совокупности наблюдений к последовательности их рангов называется ранжированием.
Ранговые и номинальные значения при вводе данных следует обозначать целыми числами.
В целях классификации применимости статистических методов будем различать следующие типы исходных данных:
1. одна выборка – совокупность измерений одной количественной, номинальной или ранговой переменной, произведенных в ходе эксперимента, опроса или наблюдения. Для одной выборки используются статистические методы описательной статистики.
Выборка может быть: неупорядоченная и структурированная (упорядоченная).
2. несколько выборок - совокупность измерений нескольких количественных, номинальных или ранговых переменных, произведенных в ходе эксперимента. Выборки могут быть:
- независимые - получены в эксперименте независимо друг от друга;
- зависимые – значения данных переменных каким-то образом согласованы (связаны) друг с другом в имеющихся наблюдениях.
Приведем типичные примеры зависимых переменных: рост человека связан с весом, потому что обычно высокие индивиды тяжелее низких; IQ (коэффициент интеллекта) связан с количеством ошибок в тесте, так как люди с высоким IQ, как правило, делают меньше ошибок, цена винчестера связана с его объемом и т.д.
Для экспериментальной педагогики характерна постановка исследований, преследующих цель выявления эффективности педагогических средств путем сравнения достижений или свойств одной и той же группы учащихся в разные периоды времени (такие группы получили название зависимых выборок) или разных групп учащихся (независимые выборки).
3. временной ряд или процесс – представляет собой значение количественной переменной (отклика), измеренные через равные интервалы значений другой количественной переменной (параметра). Например, время измерения. В качестве исходных данных рассматриваются, как правило, значения переменной отклика.
4. связные временные ряды – синхронные по времени измерения одной переменной в разных точках (объектах) или же измерения нескольких переменных в одной точке (объекте);
5. многомерные данные – представляются для статистического анализа в виде прямоугольной матрицы. Это могут быть измерения значений переменных у нескольких объектов или в нескольких точках, или же это могут быть измерения значений переменных у одного объекта в различные моменты времени или при различных состояниях.
Первый раздел математической статистики – описательная статистика – предназначен для представления данных в удобном виде и описания информации в терминах математической статистики и теории вероятностей.
Основной величиной в статистических измерениях является единица статистической совокупности (например, любой из критериев оценки качества педагога-исследователя). Единица статистической совокупности характеризуется набором признаков или параметров. Значения каждого параметра или признака могут быть различными и в целом образовывать ряд случайных значений x1, х2, …, хn.
Переменная (variable) - это параметр измерения, который можно контролировать или которым можно манипулировать в исследовании. Так как значения переменных не постоянны, нужно научиться описывать их изменчивость.
Для этого придуманы описательные или дескриптивные статистики: минимум, максимум, среднее, дисперсия, стандартное отклонение, медиана, квартили, мода.
Относительное значение параметра - это отношение числа объектов, имеющих этот показатель, к величине выборки. Выражается относительным числом или в процентах (процентное значение).
Пример: Успеваемость в классе = числу положительных итоговых отметок, деленному на число всех учащихся класса. Умножение этого значения на 100 дает успеваемость в процентах. 25/100=25%
Удельное значение данного признака - это расчетная величина, показывающая количество объектов с данным показателем, которое содержалось бы в условной выборке, состоящей из 10, или 100, 1000 и т. д. объектов.
Пример. Для сравнения уровня правонарушений в разных регионах берется удельная величина - количество правонарушений на 1000 человек (N)
Минимум и максимум — это минимальное и максимальное значения переменной.
Среднее (оценка среднего, выборочное среднее) — сумма значений переменной, деленная на n (число значений переменной). Если вы имеете значения Х(1), . X(N), то формула для выборочного среднего имеет вид:
¯ x= (1)
Пример: Наблюдение посещаемости четырех внеклассных мероприятий в экспериментальном (20 учащихся) и контрольном (30 учащихся) классах дали значения (соответственно): 18, 20, 20, 18 и 15, 23, 10, 28. Среднее значение посещаемости в обоих классах получается одинаковое - 19. Однако видно, что в контрольном классе этот показатель подчинен воздействию каких-то специфических факторов.
Выборочное среднее является той точкой, сумма отклонений наблюдений от которой равна 0. Формально это записывается следующим образом:
(¯ x - х1) + (¯ x - х2) + . + (¯ x - хn) =0
Для оценки степени разброса (отклонения) какого-то показателя от его среднего значения, наряду с максимальным и минимальным значениями, используются понятия дисперсии и стандартного отклонения.
Дисперсия выборки или выборочная дисперсия (от английского variance) – это мера изменчивости переменной. Термин впервые введен Фишером в 1918 году. Выборочная дисперсия вычисляется по формуле:
где ¯ x — выборочное среднее,
N — число наблюдений в выборке.
Дисперсия меняется от нуля до бесконечности. Крайнее значение 0 означает отсутствие изменчивости, когда значения переменной постоянны.
Стандартное отклонение, среднее квадратическое отклонение (от английского standard deviation) вычисляется как корень квадратный из дисперсии. Чем выше дисперсия или стандартное отклонение, тем сильнее разбросаны значения переменной относительно среднего.
Пример: Для предыдущего случая имеем
Это означает, что в одном классе посещаемость высокая, стабильная, а в другом - отличается непостоянством.
Медиана разбивает выборку на две равные части. Половина значений переменной лежит ниже медианы, половина — выше. Медиана дает общее представление о том, где сосредоточены значения переменной, иными словами, где находится ее центр. В некоторых случаях, например при описании доходов населения, медиана более удобна, чем среднее.
Рассмотрим способы определения медианы при различных значениях N. Для нахождения медианы измерения записывают в ряд по возрастанию значений. Если число измерений N нечетное, то медиана численно равна значению этого ряда, стоящему точно в середине, или на (N+1)/2 месте. Например, медиана пяти измерений: 10, 17, 21, 24, 25 – равна 21 – значению, стоящему на третьем месте (N+1)/2=(5+1)/2=3.
Если число измерений четное, то медиана численно равна среднему арифметическому значений ряда, стоящих в середине, или на N/2 и N/2+1 местах. Например, медиана восьми измерений: 5, 5, 6, 7, 8, 8, 9, 9 – равна 7,5 (7+8)/2=7,5 – среднему арифметическому значений ряда, стоящих на четвертом и пятом местах (N/2=8/2=4 и N/2+1=4+1=5).
Квартили представляют собой значения, которые делят две половины выборки (разбитые медианой) еще раз пополам (от слова кварта — четверть).
Различают верхнюю квартиль, которая больше медианы и делит пополам верхнюю часть выборки (значения переменной больше медианы), и нижнюю квартиль, которая меньше медианы и делит пополам нижнюю часть выборки.
Нижнюю квартиль часто обозначают символом 25%, это означает, что 25% значений переменной меньше нижней квартили.
Верхнюю квартиль часто обозначают символом 75%, это означает, что 75% значений переменной меньше верхней квартили.
Таким образом, три точки — нижняя квартиль, медиана и верхняя квартиль - делят выборку на 4 равные части.
¼ наблюдений лежит между минимальным значением и нижней квартилью, ¼ - между нижней квартилью и медианой, ¼ - между медианой и верхней квартилью, ¼ - между верхней квартилью и максимальным значением выборки.
Ассиметрия – это свойство распределения выборки, которое характеризует несимметричность распределения случайной величины (СВ). На практике симметричные распределения встречаются редко и чтобы выявить и оценить степень асимметрии, вводят следующую меру:
Асимметрия бывает положительной и отрицательной. Положительная сдвигается влево, а отрицательная – вправо.
Эксцесс – это мера крутости кривой распределения.
Кривая распределения может быть островершинной, плосковершинной, средне вершинной. Эти четыре момента составляют набор особенностей распределения при анализе данных. Для нормального распределения А=0, Е=0.
Случайной называют такую величину, которая принимает значения в зависимости от стечения случайных обстоятельств. Различают дискретныеи случайные непрерывные величины.
Дискретной называют величину, если она принимает счетное множество значений. (Пример: число пациентов на приеме у врача, число букв на странице, число молекул в заданном объеме).
Непрерывнойназывают величину, которая может принимать значения внутри некоторого интервала. (Пример: температура воздуха, масса тела, рост человека и т.д.)
Законом распределения случайной величины называется совокупность возможных значений этой величины и, соответствующих этим значениям, вероятностей (или частот встречаемости).
| x | x1 | x2 | x3 | x4 | . | xn |
| p | р1 | р2 | р3 | р4 | . | pn |
| x | x1 | x2 | x3 | x4 | . | xn |
| m | m1 | m2 | m3 | m4 | . | mn |
ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН.
Во многих случаях наряду с распределением случайной величины или вместо него информацию об этих величинах могут дать числовые параметры , получившие название числовых характеристик случайной величины. Наиболее употребительные из них:
1.Математическое ожидание - (среднее значение) случайной величины есть сумма произведений всех возможных ее значений на вероятности этих значений:
2.Дисперсия случайной величины:
3.Среднее квадратичное отклонение:
Правило “ТРЕХ СИГМ” - если случайная величина распределена по нормальному закону, то отклонение этой величины от среднего значения по абсолютной величине не превосходит утроенного среднего квадратичного отклонения
ЗАОН ГАУССА – НОРМАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ
Часто встречаются величины, распределенные по нормальному закону (закон Гаусса). Главная особенность: он является предельным законом, к которому приближаются другие законы распределения.
Случайная величина распределена по нормальному закону, если ее плотность вероятности имеет вид:
M(X) - математическое ожидание случайной величины;
s - среднее квадратичное отклонение .
| График плотности вероятности нормально распределённой величины |
Плотность вероятности (функция распределения) показывает, как меняется вероятность, отнесенная к интервалу dx случайной величины, в зависимости от значения самой величины:
ОСНОВНЫЕ ПОНЯТИЯ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
Математическая статистика - раздел прикладной математики, непосредственно примыкающий к теории вероятностей. Основное отличие математической статистики от теории вероятностей состоит в том, что в математической статистике рассматриваются не действия над законами распределения и числовыми характеристиками случайных величин, а приближенные методы отыскания этих законов и числовых характеристик по результатам экспериментов.
Основными понятиями математической статистики являются:
1. Генеральная совокупность;
2. выборка;
3. вариационный ряд;
4. мода;
5. медиана;
6. процентиль,
7. полигон частот,
8. гистограмма.
Генеральная совокупность- большая статистическая совокупность, из которой отбирается часть объектов для исследования
(Пример: все население области, студенты вузов данного города и т.д.)
Выборка (выборочная совокупность) - множество объектов, отобранных из генеральной совокупности.
Вариационный ряд- статистическое распределение, состоящее из вариант (значений случайной величины) и соответствующих им частот.
x - значение случайной величины (масса девочек в возрасте 10 лет);
m- частота встречаемости.
Мода – значение случайной величины, которому соответствует наибольшая частота встречаемости. (В приведенном выше примере моде соответствует значение 24 кг, оно встречается чаще других: m = 20).
Медиана – значение случайной величины, которое делит распределение пополам: половина значений расположена правее медианы, половина (не больше) – левее.
1, 1, 1, 1, 1. 1, 2, 2, 2, 3, 3, 4, 4, 5, 5, 5, 5, 6, 6, 7, 7, 7, 7, 7, 7, 8, 8, 8, 8, 8, 8, 9, 9, 9, 10, 10, 10, 10, 10, 10
В примере мы наблюдаем 40 значений случайной величины. Все значения расположены в порядке возрастания с учетом частоты их встречаемости. Видно, что справа от выделенного значения 7 расположены 20 (половина) из 40 значений. Стало быть, 7 – это медиана.
Для характеристики разброса найдем значения, не выше которых оказалось 25 и 75% результатов измерения. Эти величины называются 25-м и 75-м процентилями. Если медиана делит распределение пополам, то 25-й и 75-й процентили отсекают от него по четвертушке. (Саму медиану, кстати, можно считать 50-м процентилем.) Как видно из примера, 25-й и 75-й процентили равны соответственно 3 и 8.
Используют дискретное(точечное) статистическое распределение инепрерывное(интервальное) статистическое распределение.
Для наглядности статистические распределения изображают графически в виде полигона частот или - гистограммы.
Полигон частот- ломаная линия, отрезки которой соединяют точки с координатами (x1,m1), (x2,m2), . или для полигона относительных частот – с координатами (x1,р * 1), (x2,р * 2), . (Рис.1).
m mi/n f(x)
X x
Рис.1 Рис.2
Гистограмма частот- совокупность смежных прямоугольников, построенных на одной прямой линии (Рис.2), основания прямоугольников одинаковы и равны dx, а высоты равны отношению частоты к dx, или р * к dx (плотность вероятности).
| х, кг | 2,7 | 2,8 | 2,9 | 3,0 | 3,1 | 3,2 | 3,3 | 3,4 | 3,5 | 3,6 | 3,7 | 3,8 | 3,9 | 4,0 | 4,1 | 4,2 | 4,3 | 4,4 |
| m |
Полигон частот
Отношение относительной частоты к ширине интервала носит название плотности вероятности f(x)=mi / n dx = p*i / dx
Пример построения гистограммы .
Воспользуемся данными предыдущего примера.
1. Расчет количества классовых интервалов
гдеn - число наблюдений. В нашем случае n = 100. Следовательно :
Класс подмножеств данного множества X, содержащий само это множество, пустое подмножество и замкнутый относительно конечных объединений, пересечений и дополнений.
Асимптотически нормальная оценка
Так называется оценка неизвестного параметра, которая после соответствующего нормирования (см. формулу ниже) слабо сходится к нормальному распределению с параметрами 0 и . Последний параметр называют коэффициентом рассеивания.
Асимптотически нормальные оценки встречаются очень часто. Их можно использовать для построения асимптотических доверительных интервалов (см).
Асимптотические понятия
Поскольку в математической статистике основным объектом является выборка, то асимптотика изучается в той ситуации, когда объем выборки неограниченно увеличивается. То, что в пределе (для выборок бесконечного объема) обладает нужными свойствами, и называют асимптотическим. Например, асимптотически несмещенная или асимптотически эффективная оценка, асимптотический доверительный интервал, асимптотически наиболее мощный критерий и т.д.
Конечно, следует понимать, что на практике выборка бесконечного объема невозможна, поэтому асимптотические понятия используются в приближенном смысле, причем это использование оправдано только тогда, когда объем выборки достаточно велик (это понятие, между прочим, тоже нуждается в уточнении в конкретном контексте решаемых задач).
Асимптотический метод сравнения оценок
Из двух асимптотически нормальных оценок та считается лучшей, у которой коэффициент рассеивания меньше.
Беренса - Фишера проблема
Так называют проверку гипотезы частичной однородности в случае двух выборок из нормальных распределений (равенства средних и/или дисперсий).
Проблема построения наиболее мощных критериев для этой проверки до сих пор во многом открыта. Проблема полностью решена лишь для независимых выборок. Это решение достаточно полно изучается в настоящем курсе.
Борелевские множества
Элементы борелевской сигма-алгебры. В одномерном случае эта сигма-алгебра порождается всевозможными полубесконечными (слева) открытыми интервалами, в конечномерном - всеми декартовыми произведениями одномерных борелевских множеств.
Построение бесконечномерных борелевских множеств связано с цилиндрическими множествами (см.). Борелевская сигма-алгебра в этом случае порождается классом всех цилиндрических множеств.
В конечномерном случае все измеримые по Риману множества являются борелевским, поэтому в практических задачах никакие множества, кроме борелевских, не встречаются. Тем не менее, без формальных требований к набору всех изучаемых множеств, подобному определению борелевских множеств, содержательная и строгая теория, по-видимому, невозможна.
Вариационный ряд
Так называют выборку, упорядоченную по возрастанию (неубыванию) ее элементов. Конечно же, при этом положение каждого отдельного элемента вариационного ряда определяется всей выборкой в целом, поэтому j-й член вариационного ряда называют j-й порядковой статистикой. Для того, чтобы члены вариационного ряда разбили на непересекающиеся отрезки всю числовую прямую, иногда вводят два фиктивных крайних члена вариационного ряда - нулевой (равный минус бесконечности) и (n+1)-й (равный плюс бесконечности).
Выборка
С практической точки зрения - набор чисел, полученный в результате многократных независимых наблюдений некоторой случайной величины.
С теоретической точки зрения - многомерный случайный вектор с независимыми координатами, каждая из которых имеет одно и то же распределение (совпадающее с распределением основной случайной величины).
Выборочное пространство
Выборочное пространство является полным аналогом вероятностного пространства в теории вероятностей и играет в математической статистике роль основной структуры. Традиционно оно состоит из трех объектов. Первый - множество всех возможных выборок, которые могут получиться при наблюдениях основной величины и потенциально обладают бесконечными объемами. Второй - борелевская сигма-алгебра подмножеств первого множества. Третий - вероятность, определенная на втором элементе и строящаяся по распределению наблюдаемой случайной величины по теореме Каратеодори следующим образом: на цилиндрических множествах эта вероятность равна произведению вероятностей попадания наблюдаемой случайной величины во все нетривиальные борелевские основания этих множеств. На остальных элементах второго объекта она задается как продолжение с алгебры цилиндрических множеств на все борелевскую сигма-алгебру уже построенных своих значений. Такое построение возможно (и единственно!) согласно упомянутой теореме Каратеодори.
Неформально третий объект можно интерпретировать как вероятность попадания бесконечномерного вектора с независимыми одинаково распределенными координатами в борелевское бесконечномерное множество.
Аналогом понятия случайной величины здесь, таким образом, является понятие статистики.
Гипотеза статистическая
Предположение о наблюдаемых случайных величинах, которое может быть проверено, если известны теоретические распределения самих величин и совместные распределения. Следует понимать, что это лишь пояснение понятия статистической гипотезы, а не строгое его определение.
Дать совершенно строгое определение понятия гипотеза, видимо, невозможно.
Математическая статистика - это методология, которая позволяет принимать взвешенные решения среди неопределенных условий. Исследование способов сбора и систематизации данных, обработки итоговых результатов опытов и экспериментов с массовыми случайностями и обнаружение каких-либо закономерностей - это то, чем занимается данный раздел математики. Рассмотрим основные понятия математической статистики.
Разница с теорией вероятностей
Методы математической статистики тесно пересекаются с теорией вероятностей. Оба раздела математики занимаются исследованием многочисленных случайных явлений. Связывают две дисциплины между собой предельные теоремы. Однако существует большая разница между этими науками. Если теория вероятностей определяет на основе математической модели характеристики процесса в реальном мире, то математическая статистика делает наоборот - устанавливает свойства модели на основе наблюдаемой информации.

Этапы
Применение математической статистики может осуществляться только по отношению к случайным событиям или процессам, а точнее, к данным, полученным из наблюдения за ними. И происходит это в несколько этапов. Сначала данные экспериментов и опытов проходят определенную обработку. Их упорядочивают для наглядности и удобства анализа. Затем производится точная или приблизительная оценка требуемых параметров наблюдаемого случайного процесса. Ими могут быть:
- оценка вероятности того или иного события (вероятность его изначально неизвестна);
- изучение поведения неопределенной функции распределения;
- оценка математического ожидания;
- оценка дисперсии
- и т. д.
Вам будет интересно: Бордовый цвет: как получить и правильно смешать? Цветовые решения, оттенки и фото
В третий этап можно выделить проверку каких-либо гипотез, поставленных до проведения анализа, т. е. получение ответа на вопрос о том, насколько результаты экспериментов соответствуют теоретическим выкладкам. По факту, это основной этап математической статистики. Примером может быть рассмотрение вопроса о том, находится ли поведение наблюдаемого случайного процесса в пределах нормального закона распределения.
Генеральная совокупность
В основные понятия математической статистики входят генеральная и выборочная совокупности. Данная дисциплина занимается изучением множества некоторых объектов касательно какого-либо свойства. В качестве примера можно привести работу таксиста. Рассмотрим эти случайные величины:
- загруженность или количество клиентов: в сутки, до обеда, после обеда, . ;
- среднее время поездки;
- количество поступающих заявок или их привязанность к районам города и многое другое.
Вам будет интересно: "Романист" - это что-то связанное с литературой? Вы правы на треть
Стоит также отметить, что можно исследовать совокупность подобных случайных процессов, которая также будет представлять собой случайную величину, над которой можно проводить наблюдения.

Итак, в методах математической статистики все множество исследуемых объектов или результатов всевозможных наблюдений, которые проводятся в одинаковых условиях над взятым объектом, называется генеральной совокупностью. Иными словами, математически более строго, это случайная величина, которая определена в пространстве элементарных событий, с обозначенным в нем классом подмножеств, элементы которого обладают известной вероятностью.
Выборочная совокупность
Бывают случаи, когда невозможно или нецелесообразно по каким-то причинам (стоимость, затраты времени) провести сплошное исследование для изучения каждого объекта. Например, открывать каждую банку запечатанного варенья для контроля его качества - сомнительное решение, а попытка оценить траекторию каждой молекулы воздуха в кубическом метре - невыполнима. В таких случаях используют способ выборочного наблюдения: из генеральной совокупности производится выбор (как правило, случайным образом) некоторого количества объектов, и их подвергают их анализу.
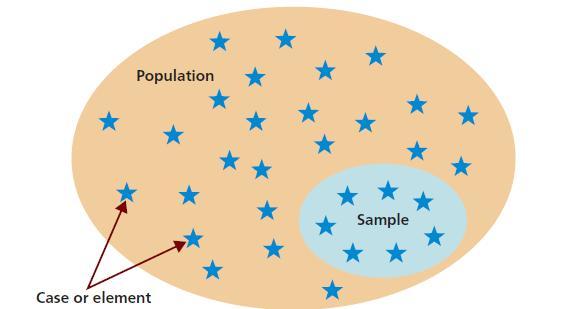
Эти понятия могут казаться сложными поначалу. Поэтому, чтобы наиболее полно понять тему, нужно изучать учебник В. Е. Гмурмана "Теория вероятностей и математическая статистика". Таким образом, выборочная совокупность или выборка - это ряд объектов, выбранных случайным образом из генерального множества. Говоря строгим математическим языком, это последовательность независимых, равномерно распределенных случайных величин, для каждой из которых распределение совпадает с тем, которое обозначено для генеральной случайной величины.
Основные понятия
Рассмотрим вкратце ряд других основных понятий математической статистики. Число объектов в генеральной совокупности или выборке называется объемом. Значения выборки, которые получают в ходе эксперимента, называются реализацией выборки. Чтобы оценка генеральной совокупности на основе выборочной была достоверной, важно иметь так называемую представительную или репрезентативную выборку. Это значит, что выборка должна в полном объеме представлять генеральную совокупность. Добиться этого можно только в том случае, когда все элементы генеральной совокупности имеют равную вероятность оказаться в выборке.

Выборки различают с возвращением и без возвращения. В первом случае в содержимом выборки повторный элемент возвращается в генеральное множество, во втором - нет. Обычно на практике применяется выборка без возвращений. Следует также отметить, что объем генеральной совокупности всегда значительно превосходит объем выборки. Существует множество вариантов процесса выборки:
- простой - элементы выбираются случайным образом по одному;
- типизированный - генеральная совокупность разделяется на типы, и из каждого производится выбор; примером может послужить опрос жителей: мужчины и женщины раздельно;
- механический - например, выбрать каждый 10-й элемент;
- серийный - выбор производится сериями элементов.
Статистическое распределение
Согласно Гмурману, теория вероятностей и математическая статистика являются крайне важными дисциплинами в научном мире, особенно в практической его части. Рассмотрим статистическое распределение выборки.
Пусть у нас имеется группа студентов, в которой было проведено тестирование по математике. В итоге у нас есть совокупность оценок: 5, 3, 1, 4, 3, 4, 2, 5, 4, 4, 5 - это наш первичный статистический материал.
Первым делом нам нужно его упорядочить, или провести операцию ранжирования: 1, 2, 3, 3, 4, 4, 4, 4, 5, 5, 5 - и получить, таким образом, вариационный ряд. Количество повторений каждой из оценок при этом называется частотой оценки, а их отношение к объему выборки - относительной частотой. Составим таблицу статистического распределения выборки, или просто статистический ряд:
| ai | 1 | 2 | 3 | 4 | 5 |
| pi | 1 | 1 | 2 | 4 | 3 |
| ai | 1 | 2 | 3 | 4 | 5 |
| pi* | 1/11 | 1/11 | 2/11 | 4/11 | 3/11 |
Пусть у нас имеется случайная величина, над которой мы будем проводить серию экспериментов и смотреть, какое значение принимает эта величина. Допустим, она приняла значение a1 - m1 раз; a2 - m2 раз и т.д. Объемом данной выборки будет m1 + . + mk = m. Множество ai, где i меняется от 1 до k, представляет собой статистический ряд.
Интервальное распределение
В книге В. Е. Гмурмана "Теория вероятностей и математическая статистика" также представлен интервальный статистический ряд. Его составление возможно, когда значение исследуемого признака непрерывно в определенном интервале, и число значений велико. Рассмотрим группу студентов, а точнее, их рост: 163, 180, 185, 172, 161, 171, 189, 157, 165, 174, 180, 181, 175, 182, 167, 159, 173, 171, 164, 179, 160, 180, 166, 178, 156, 180, 189, 173, 174, 175 - всего 30 студентов. Очевидно, что рост человека - это непрерывная величина. Нам нужно определить шаг интервала. Для этого используется формула Стерджеса.
| h= | max - min | = | 190 - 156 | = | 33 | = | 5,59 |
| 1+log2m | 1+log230 | 5,9 |
Таким образом, за размер интервала можно принять величину 6. Также следует сказать, что значение 1+log2m - это формула для определения количества интервалов (разумеется, с округлением). Таким образом, получается по формулам 6 интервалов, каждый из которых имеет размер 6. И первым значением начального интервала будет число, определяемое по формуле: min - h/2 = 156 - 6/2 = 153. Составим таблицу, которая будет содержать интервалы и число студентов, рост которых попал в определенный интервал.
Разумеется, это далеко не все, ибо в математической статистике формул куда больше. Мы рассмотрели лишь некоторые базовые понятия.
График распределения
В основные понятия математической статистики также входит графическое представление распределения, которое отличается наглядностью. Существует два вида графиков: полигон и гистограмма. Первый используется для дискретного статистического ряда. А для непрерывного распределения, соответственно, второй.
Читайте также:

