Определение равных векторов кратко

Обновлено: 30.06.2024

Основными характеристиками вектора в пространстве и на плоскости являются его длина и направление, и именно на этом основано определение равенства векторов.

Для начала введем понятие коллинеарности.

Коллинеарность — характеристика взаиморасположения ненулевых векторов. Векторы коллинеарны, если расположены на одной прямой или параллельных прямых. Коллинеарные векторы допустимо называть параллельными.

Из определения нулевого вектора (вектор, у которого начальная и конечная точки совпадают, и длина равна нулю) ясно, что нулевой вектор коллинеарен любому другому вектору.

Если направления коллинеарных векторов совпадают, то их называют сонаправленными и обозначают b → ↑ ↑ d → , если нет — противоположно направленными и обозначают b → ↑ ↓ d → .

Равными считают те векторы, длины которых равны, а направления совпадают.

Понятие, признаки, какие нужны условия

Понятие равенства векторов применяется не только в геометрии, но и в алгебре, и особенно часто в физике, где действующие на тела сила представляют в векторном виде.

Необходимые признаки следуют из определения равных векторов. Итак, векторы равны, если:

их модули или координаты равны;
они сонаправлены.

Остановимся подробнее на первом признаке. Модуль — длина вектора обозначается как \left|\overrightarrow b\right|. Формула для вычисления длины вектора на плоскости имеет вид:

Под корнем находится сумма координат вектора, то есть векторы равны, если доказано либо равенство их модулей, либо координат.

Необходимым условием равенства векторов является сочетание двух признаков: векторы должны быть сонаправлены, а их длины равными.

Отметим, что наличие только одного из признаков не делает векторы равными. Так, противоположно направленные векторы с одинаковыми длинами не равны. Сонаправленные векторы с отличными по величине модулями также нельзя назвать равными.

Доказательство теоремы, формулы

Равные векторы обладают следующими свойствами:

Вектор равен самому себе.
Для равных векторов справедливо тождество: b → = d → ⇔ d → = b → .
Если векторы равны третьему, то они равны друг другу.

Доказательство. Первые два свойства прямо следуют из определения равенства векторов. Докажем третье свойство. Для этого воспользуемся правилом параллельного переноса. Пусть имеются три вектора, при этом b → = d → и f → = d → . Начальную и конечную граничные точки f → совместим с соответствующими граничными точками d → . Так как f → = d → , векторы совпадут. По условию b → = d → , а если f → и d → совпали, то b → = f → . Теорема доказана.

Кратко остановимся на используемых для решения задач формулы математических операций с векторами:

Умножение b → на число k: d → = k · b → .
Сложение и вычитание векторов производят по методу треугольника.

Примеры задач для 9 класса

Дано: d → = b → . Известны координаты вектора b → ( 2 ; 21 ) и одна координата вектора d → ( 3 ; y ) . Найти координату y d → .

По условию задачи векторы равны, а значит, равных их модули. Составим уравнение с неизвестной переменной — y.

2 2 + ( 21 ) 2 = 3 2 + y 2

Откуда: 25 = 9 + y 2 ⇒ y = 4 .

Дано: два вектора M N → и K L → такие, что MN=KL. По точкам M и L построен отрезок ML, по точкам N и K — NK. Доказать, что середины ML и NK совпадают.

Сделаем рисунок по условию задачи.

Видно, что MNLK — параллелограмм. Тогда ML и NK являются диагоналями MNLK. По свойству параллелограмма, точка пересечения диагоналей делит их пополам. То есть середина ML совпадет с серединой NK, что и требовалось доказать.

Дано: прямоугольник KLMN. Известны длины сторон: KL=6; LM=8. На отрезке KL обозначена точка O, при этом KO=OL. Найти длину N O → .

Прямоугольник — частный случай параллелограмма, то есть его противоположные стороны равны. Длину N O → найдем как гипотенузу прямоугольного треугольника NKO.

N O → = K O 2 + N K 2 = K L 2 2 + L M 2 = 9 + 64 = 73

Определить форму фигуры, заданной точками H, D, F, G, если имеется свободно расположенная на плоскости точка O такая, что O F → - O D → = O G → - O H → .

Для решения задачи необходимо последовательно выполнить чертеж по известным условиям. Обозначим точку О, теперь проведем из точки O F → и O D → . По методу треугольника построим вектор D F → , равный разности O F → и O D → . Затем из точки О также проведем векторы O H → , O G → и результирующий H G → . Получили четырехугольник. HDFG. По условию противоположные стороны DF и HG равны, значит, HDFG — параллелограмм.

В статье пойдет речь о том, что такое вектор, что он из себя представляет в геометрическом смысле, введем вытекающие понятия.

Для начала дадим определение:

Вектор – это направленный отрезок прямой.

Исходя из определения, под вектором в геометрии отрезок на плоскости или в пространстве, который имеет направление, и это направление задается началом и концом.

В математике для обозначения вектора обычно используют строчные латинские буквы, однако над вектором всегда ставится небольшая стрелочка, например a → . Если известны граничные точки вектора – его начало и конец, к примеру A и B , то вектор обозначается так A B → .

Нулевой вектор

Под нулевым вектором 0 → будем понимать любую точку плоскости или пространства.

Из определения становится очевидным, что нулевой вектор может иметь любое направление на плоскости и в пространстве.

Длина вектора

Под длиной вектора A B → понимается число, большее либо равное 0, и равное длине отрезка АВ.

Длину вектора A B → принято обозначать так A B → .

Понятия модуль вектора и длина вектора равносильны, потому что его обозначение совпадает со знаком модуля. Поэтому длину вектора также называют его модулем. Однако грамотнее использовать термин "длина вектора". Очевидно, что длина нулевого вектора принимает значение ноль.

Коллинеарность векторов

Два вектора лежащие на одной прямой или на параллельных прямых называются коллинеарными.

Два вектора не лежащие на одной прямой или на параллельных прямых называются неколлинеарными.

Следует запомнить, что Нулевой вектор всегда коллинеарен любому другому вектору, так как он может принимать любое направление.

Коллиниарные векторы в свою очередь тоже можно разделить на два класса: сонаправленные и противоположно направленные.

Направление векторов

Сонаправленными векторами называют два коллинеарных вектора a → и b → , у которых направления совпадают, такие векторы обозначаются так a → ↑ ↑ b → .

Противоположно направленными векторами называются два коллинеарных вектора a → и b → , у которых направления не совпадают, т.е. являются противоположными, такие векторы обозначаются следующим образом a → ↑ ↓ b → .

Считается, что нулевой вектор является сонаправленым к любым другим векторам.

Равные и противоположные векторы

Равными называются сонаправленные вектора, у которых длины равны.

Противопожными называются противоположно направленные вектора, у которых их длины равны.

Введенные выше понятия позволяют нам рассматривать векторы без привязки к конкретным точкам. Иначе говоря, можно заменить вектор равным ему вектором, отложенным от любой точки.

Пусть заданы два произвольных вектора на плоскости или в пространстве a → и b → . Отложим от некоторой точки O плоскости или пространства векторы O A → = a → и O B → = b → . Лучи OA и OB образуют угол ∠ A O B = φ .

Углы между векторами

Угол φ = ∠ A O B называется углом между векторами a → = O A → и b → = O B → .

Очевидно, что угол между сонаправленными векторами равен нулю градусам (или нулю радиан), так как сонаправленные векторы лежат на одной или на параллельных прямых и имеют одинаковое направление, а угол между противоположно направленными векторами равен 180 градусам (или π радиан), так как противоположно направленные векторы лежат на одной или на параллельных прямых, но имеют противоположные направления.

Перпендикулярными называются два вектора, угол между которыми равен 90 градусам (или π 2 радиан).

Определение. Вектора a и b называются равными, если они имеют одинаковую длину, лежат на параллельных прямых или на одной прямой, и направлены в одном направлении. (рис. 1).

То есть, два вектора равны, если они коллинеарные, сонаправленые и имеют равные длины:

a = b , если a ↑↑ b и | a | = | b |.

рис. 1

Примеры задач на равенство векторов

Примеры плоских задач на равенство векторов

a = b - так как их координаты равны,
a ≠ c - так как их координаты не равны,
b ≠ c - так как их координаты не равны.

Проверим равенство компонентов векторов
a_x = b_x = 1
a_y = b_y => 8 = 2 n => n = 8/2 = 4

Ответ: при n = 4 вектора a и b равны.

Примеры пространственных задач на равенство векторов

a = c - так как их координаты равны,
a ≠ b - так как их координаты не равны,
b ≠ c - так как их координаты не равны.

Проверим равенство компонентов векторов
a_x = b_x = 1
a_y = b_y = 2
a_z = b_z => 4 = 2 n => n = 4/2 = 2

Ответ: при n = 2 вектора a и b равны.

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

В различных школьных учебниках определение равных векторов даётся по-разному.

В классическом учебнике Погорелова А. В. понятие равных векторов вводится с помощью параллельного переноса.

Два вектора называются равными, если они совмещаются параллельным переносом.

(то есть существует параллельный перенос, который переводит начало и конец одного вектора соответственно в начало и конец другого).

Например, изображенные на рисунке

$\overrightarrow <AB> $

$\overrightarrow <CD> $

Равенство векторов обозначают так:

$\overrightarrow <AB> = \overrightarrow$

(Свойства равных векторов)

1) Равные векторы сонаправлены и имеют равные длины.

2) Равные векторы имеют равные координаты.

3) От любой точки можно отложить вектор, равный данному, и притом только один.

1) 1-е свойство вытекает непосредственно из определения равных векторов и свойств параллельного переноса.

2) Пусть дан вектор

$\overrightarrow <AB> $

с началом в точке A(x₁; y₁) и концом в точке B(x₂; y₂).

По определению равных векторов, вектор

$\overrightarrow <A^/ B^/ > $

равный данному, получен из

$\overrightarrow <AB> $

Если этот параллельный перенос задан формулами

$\left\< \begin x^/ = x + m, \\ y^/ = y + n, \\ \end \right.$

Найдём координаты каждого из векторов:

$\overrightarrow <AB> (x_2 - x_1 ;y_2 - y_1 ),$

$\overrightarrow <A^/ B^/ > ((x_2 + m) - (x_1 + m);(y_2 + n) - (y_1 + n)),$

$\overrightarrow <A^/ B^/ > (x_2 + m - x_1 - m;y_2 + n - y_1 - n),$

$\overrightarrow <A^/ B^/ > (x_2 - x_1 ;y_2 - y_1 ).$

То есть координаты равных векторов

$\overrightarrow <AB> $

$\overrightarrow <A^/ B^/ > $

Что и требовалось доказать.

Таким образом, координаты задают длину и направление вектора, но не фиксируют его.

3) Пусть даны вектор

$\overrightarrow <AB> $

и точка C.
Существует и притом единственный параллельный перенос, при котором точка A переходит в точку C — параллельный перенос на вектор

$\overrightarrow <AC> $

При таком параллельном переносе вектор

$\overrightarrow <AB> $

переходит в вектор

$\overrightarrow <CD.> $

По определению равных векторов,

$\overrightarrow <CD> = \overrightarrow .$

Что и требовалось доказать.

На практике, если требуется отложить от некоторой точки вектор, равный данному, удобно это делать с помощью параллелограмма (если точка, от которой откладывается вектор, не лежит на прямой, содержащей этот вектор).

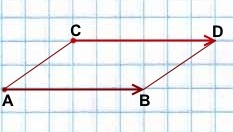
Например,

$\overrightarrow <CD> ,$

отложенный от точки C, равен вектору

$\overrightarrow <AB> $

(Признаки равенства векторов)

1) Если векторы сонаправлены и имеют одинаковые длины, то они равны.

2) Если у векторов соответствующие координаты равны, то векторы равны.

1) Пусть векторы

$\overrightarrow <AB> $

$\overrightarrow <CD> $

сонаправлены и имеют одинаковые длины.

Параллельный перенос, который переводит точку A в точку C, совмещает луч CD с лучом AB (поскольку векторы одинаково направлены). А так как длины отрезков CD и AB равны, то точка D при этом совместится с точкой B. Таким образом, этот параллельный перенос вектор

$\overrightarrow <AB> $

переводит в вектор

$\overrightarrow <CD> $

По определению равных векторов,

$\overrightarrow <CD> = \overrightarrow .$

Что и требовалось доказать.

2) Пусть векторы

$\overrightarrow <AB> $

$\overrightarrow <A^/ B^/ > $

Параллельный перенос, заданный формулами

$\left\< \begin x^/ = x - x_1 + x_1^/ , \\ y^/ = y - y_1 + y_1^/ , \\ \end \right.$

переводит точку A в точку A′, точку B — в точку B′, то есть совмещает векторы

$\overrightarrow <AB> $

$\overrightarrow <A^/ B^/ > $

А это означает, что

$\overrightarrow <A^/ B^/ > = \overrightarrow .$

Что и требовалось доказать.

В учебнике Атанасяна Л. С. и др. дано другое определение равных векторов.

Два вектора называются равными, если они сонаправлены и имеют одинаковую длину.

$\bar Вектора и$
называются равными, если они сонаправлены и имеют равные модули (рис. 1):

$\bar=\bar \Leftrightarrow \bar\uparrow \uparrow \bar\wedge \left|\bar\right|=\left|\bar\right|$

Если векторы заданы своими координатами, то они равны, если равны их соответствующие координаты:

Примеры решения задач

Задание	Определить, какие из векторов $\bar=\left(-3;\; 2\right),\ \bar=\left(1;\; 1\right)$ и $\bar<c>=\left(-3;\; 2\right)$ являются равными.
Решение	Из всех указанных векторов равными являются только векторы и $\bar<c>$ , поскольку координаты этих векторов равны.
Ответ	$\bar=\bar<c>$

Задание	При каком значении параметра векторы и $\bar=\left(-1;\; 2m\right)$ равны?
Решение	Два вектора равны, если равны их соответствующие координаты, то есть

$a_ =-1=b_ ,$

$a_ =2=2m=b_ \Rightarrow 2m=2\Rightarrow m=1$

Читайте также: