Методика изучения уравнений в основной школе

Обновлено: 02.07.2024

При изучении линии уравнений с учащимися рассматриваются следующие вопросы:

-взаимосвязь изучаемых понятий с другими линиями курса;

-общие и частные методы решения уравнений.

В процессе обучения раскрываются:

- прикладная направленность линии уравнений (при решении текстовых задач; в геометрии - при использовании метода координат; при построении моделей различных процессов и т. д.);

- теоретическая направленность (при изучении наиболее важных классов уравнений, изучении обобщенных понятий и методов и т. д.);

- направленность на установление связей с основными темами курса. Линия уравнений тесно связана с числовой и функциональной линиями. Они дополняют и обогащают друг друга. Так, например, потребность в решении нового класса уравнений способствовала введению нового числового множества и наоборот.

1) Уравнение - это равенство, содержащее неизвестное число, обозначенное буквой.

2) Равенство с переменной называется уравнением, если надо найти значения переменной, при которых оно верно.

3) Равенство с переменной называется уравнением.

4) Равенство двух функций, g(x) = f(x), заданных на общей области их определения, называется уравнением.

5) Уравнение - это высказывательная форма (предикат) вида

2. В различных определениях используется переменная или неизвестное число. Переменная величина пробегает ряд значений, не выделяя ни одного из них. Неизвестное число представляет собой буквенное обозначение конкретного числа (поэтому удобно в текстовых задачах).

3. Родовое понятие для всех этих определений -равенство. Но известно еще одно понятие, которое определяется как особый вид равенства - это тождество, школьное определение которого – равенство, верное при всех допустимых значениях переменной.

В связи с этим, в методической литературе встречаются различные точки зрения на связь между двумя понятиями.

1-я точка зрения: уравнение – частный случай тождества (Тождество – это равенство, верное при всех …, а уравнение – это равенство, верное не при всех …)

2-я точка зрения: тождество - частный случай уравнения (Тождество – это уравнение, множество решений которого все допустимые значения переменной; тогда линейное уравнение ах = в при а = 0 и в = 0 становится тождеством)

3-я точка зрения: уравнение и тождество - независимые понятия.

В уравнении равенство - это синтаксическое образование, которое может быть либо истинным, либо ложным, то есть можно говорить об условном равенстве, так как уравнение - это суждение о равенстве 2-х функций, а суждение может быть либо истинным, либо ложным. Поэтому в уравнениях запрещаются преобразования цепочкой и недопустима запись х_1,2 = (-в± )/2а.

Решение уравнений является важнейшим видом учебной деятельности. В процессе решения уравнений учащимися усваиваются математические знания, развиваются их интеллектуальные способности и творческое мышление. Линия уравнений и неравенств основана на построении и изучении математических моделей, включает вырабатывание и совершенствование техники алгебраических преобразований для решения уравнений, неравенств и систем. Значительное большинство задач о количественных отношениях и о пространственных формах окружающей действительности решается с помощью уравнений. Уравнения являются существенной частью математических средств, используемых в математическом моделировании. Существуют четыре универсальных метода решения уравнений: функционально-графический метод, метод введения новой переменной, метод разложения на множители, метод решения однородных уравнений. Каждый из этих методов решения уравнения подходит для решения любого типа уравнений. В этом их сила и универсальность. В работе изучена математическая литература и выделены логико-математические основы решения уравнений. Проведен анализ научно-методической литературы по проблеме исследования и выявлены теоретические аспекты формирования умений решать уравнения. Приведены общие методические рекомендации обучения школьников решению уравнений. Сформулированы этапы обучения школьников решению уравнений.

1. Григорян М.Э., Болдыревский П.Б. Междисциплинарная интеграция в реализации компетентностного подхода // Международный журнал прикладных и фундаментальных исследований. – 2016. – № 6–1. – С. 145–148.

2. Методика преподавания математики в средней школе: частная методика / А.Я. Блох, В.А. Гусев, Г.В. Дорофеев и др.; Составитель В.И. Мишин. – М.: Просвещение,1987. – 416 с.

4. Мордкович А.Г. Алгебра и начала анализа. 10–11 классы. Учебник для общеобразовательных учереждений. Часть 1 / А.Г. Мордкович, 10-е издание. – М.: Мнемозина, 2009. – 399 с.

5. Перевощикова Е.Н. Специфика формирования универсальных учебных действий при обучении математике в основной школе // Интеграция образования. – 2015. – Т. 19, № 2 (79). – С. 81–91.

В школьном курсе алгебры уравнения занимают важное место. Линия уравнений и неравенств основана на построении и изучении математических моделей, включает вырабатывание и совершенствование техники алгебраических преобразований для решения уравнений, неравенств и систем. В процессе изучения данной темы у учащихся формируются способности строить и исследовать математические модели при решении задач из смежных дисциплин. Значительное большинство задач о количественных отношениях и о пространственных формах окружающей действительности решается с помощью уравнений. Уравнения являются существенной частью математических средств, используемых в математическом моделировании. Установление междисциплинарных связей в образовательной практике ведет к качественному развитию общекультурных компетенций [1].

Согласно программе для классов с углубленным изучением математики в результате изучения данной дисциплины учащиеся должны научиться решать различные уравнения и использовать приобретенные знания, умения и навыки в практической деятельности. С целью овладения указанным видом учебной деятельности обучающийся в ходе освоения математики должен обладать определенными способностями (табл. 1).

Способности, которыми должен обладать ученик в ходе освоения математики

- уравнения – это математическая модель решения различных задач из математики, смежных наук, практики

- определения различных видов уравнений;

- теоремы о равносильности уравнений;

- основные приемы решения уравнений;

- общие методы решения уравнений

- решать линейные, квадратные, рациональные, показательные, логарифмические, тригонометрические уравнения;

- решать системы уравнений с двумя неизвестными;

- решать уравнения с параметрами;

- изображать на координатной плоскости решения уравнений, неравенств и систем с двумя неизвестными;

- решать текстовые задачи с помощью составления уравнений [2]

использовать приобретенные знания и умения в практической деятельности:

- для построения и изучения простейших математических моделей

Цель исследования состоит в разработке научно обоснованных методических рекомендаций по обучению учащихся естественнонаучного профиля решению уравнений.

Объект исследования: процесс обучения алгебре в классах естественнонаучного профиля.

Предмет исследования: методическая система обучения учащихся решению уравнений [3].

В соответствии с поставленной целью были определены задачи исследования:

1. Проанализировать научно-методическую литературу по теории уравнений с целью выявления теоретических аспектов формирования умений решать уравнения при обучении математике.

2. Изучив математическую литературу, выделить логико-математические основы решения уравнений.

3. Разработать общие рекомендации по методике обучения школьников решению уравнений.

Логико-математические основы решения уравнений

Теоретической основой решения уравнений является равносильность уравнений. В табл. 2 приведены основные определения и теоремы о равносильности.

Определения и теоремы о равносильности

1. Если множества корней уравнений f(x) = g(x) и p(x) = h(x) совпадают, то их называют равносильными.

2. Уравнение p(x) = h(x) называют следствием уравнения f(x) = g(x), если все корни уравнения f(x) = g(x) являются корнями уравнения p(x) = h(x)

Уравнение равносильное данному уравнению получится при следующих алгебраических преобразованиях:

1. Перенос любого члена уравнения из одной части уравнения в другую с противоположным знаком.

2. Умножение обеих частей уравнения f(x) = g(x) на одно и то же число, отличное от нуля.

3. Умножение обеих частей уравнения f(x) = g(x) на одно и то же выражение h(x), которое: 1) всюду в области определения уравнения f(x) = g(x) имеет смысл; 2) нигде в этой области не обращается в 0.

4. Возведение обеих частей уравнения f(x) = g(x) в одну и ту же нечётную степень.

5. Возведение обеих частей уравнения f(x) = g(x) в одну и ту же чётную степень, при условии, что обе части уравнения неотрицательны в области определения уравнения.

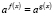
6. Переход от показательного уравнения , где a > 0, a≠ 1 к уравнению f(x) = g(x).

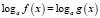
7. Переход от логарифмического уравнения , где a > 0, a ≠ 1, к уравнению f(x) = g(x), если f(x) > 0 и g(x) > 0 [4]

Рассмотрим общие принципы решения уравнений. Существует три этапа решения уравнений. Первый этап – технический. На данном этапе осуществляется переход к новому уравнению f1(x) = g1(x) или дизъюнкции уравнений f1(x) = g1(x), f2(x) = g2(x),… fn(x) = gn(x).

Для решения уравнения f(x) = g(x) нужно решить все уравнения f1(x) = g1(x), f2(x) = g2(x),… fn(x) = gn(x) и взять объединение множеств их корней.

Второй этап – анализ решения. На этом этапе анализируются все проведённые преобразования на равносильность.

На третьем этапе осуществляется проверка. Если, анализируя преобразования на втором этапе, делается вывод, что получено уравнение-следствие, то проводится проверка всех найденных корней их подстановкой в уравнение f(x) = g(x). В результате мы и получаем множество всех корней уравнения [4].

Если какое-либо из уравнений fk(x) = gk(x) не решается непосредственно, то к нему применяется тот же прием.

Существуют четыре общих универсальных метода решения уравнений: функционально-графический метод, метод введения новой переменной, метод разложения на множители, метод решения однородных уравнений. Каждый из этих методов решения уравнения подходит для решения любого типа уравнений. В этом их сила и универсальность. В таблице приведены общие методы решения уравнений.

Общие методы решения уравнений

Метод разложения на множители

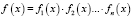
Суть метода: пусть нужно решить уравнение f(x) = 0 и пусть . Тогда уравнение f(x) = 0 можно заменить совокупностью более простых уравнений

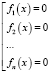
Находим корни уравнений этой совокупности, далее отобрав из них те, что принадлежат области определения уравнения f(x) = 0, получим корни уравнения f(x) = 0.

Приемы разложения: вынесение общего множителя за скобки; способ группировки; использование формул сокращенного умножения, разложение квадратного трехчлена

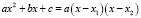
где x1 и x2 – корни квадратного трехчлена. Иногда добавляется искусственный прием: представление одного из слагаемых в виде некоторой суммы и, в частности, прибавление и вычитание одного и того же выражения с целью последующей перегруппировки слагаемых; всевозможные комбинации вышеуказанных приемов.

Суть метода: необходимо построить графики функций y = f(x), y = g(x) и найти точки их пересечения. Корнями уравнения служат абсциссы этих точек. Данный метод позволяет определить число корней, угадать значение корня, найти приближенное, а иногда и точное значение корней.

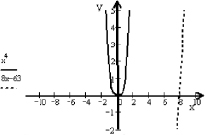
Решение уравнения графическим методом

Пример. Решим уравнение x4 – 8x + 63 = 0. Представим исходное уравнение в виде x4 = 8x – 63. Построим графики функций y = x4, y = 8x – 63.

Графики не пересекаются, а значит, исходное уравнение не имеет корней.

Ответ: нет корней.

В некоторых случаях построение графиков функций можно заменить ссылкой на какие-либо свойства функции (монотонность).

Метод введения новой переменной

Суть метода: если уравнение f(x) = 0 удалось преобразовать к виду f(g(x)) = 0, то надо ввести новую переменную y = g(x), решить уравнение f(y) = 0, далее необходимо решить совокупность уравнений

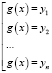
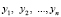
где – корни уравнения f(y) = 0.

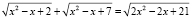
Положив y = x2 – x, получим

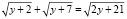
Далее имеем последовательно

, ,

, .

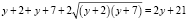
Проверка найденных значений подстановкой в исходное уравнение показывает, что y1 = 2 удовлетворяет этому уравнению, y2 = –11 – нет, это посторонний корень. Возвращаясь к переменной х, получаем уравнение x2 – x = 0, откуда находим x1 = 2, x2 = –1.

Метод решения однородных уравнений

Однородные уравнения – термин связан с понятием однородной функции.

Функция f(x; y) от двух аргументов х и у называется однородной функцией степени n, если f(kx; ky) = kn·f(x; y), где число n – степень однородной функции f(x; y).

Однородным уравнением одной переменной первого порядка называется уравнение вида

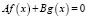
где f(x) и g(x) – функции одного вида.

Однородным уравнением одной переменной второго порядка называется уравнение вида

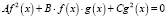
где f(x) и g(x) – функции одного вида.

Метод решения рассмотрим на примере показательных уравнений (табл. 3).

Методы решения однородных уравнений

Однородное уравнение первой степени

Однородное уравнение второй степени

;

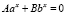
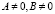
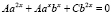
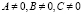
Суть метода решения

1) разделить обе части уравнения на bx, где bx ≠ 0;

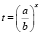
2) обозначить , t > 0;

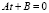
3) решив линейное уравнение , получить корень t.

4) проверить условие t > 0;

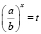
5) решить уравнение

1) разделить обе части уравнения на b2x, где b2x ≠ 0;

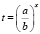
2) обозначить , t > 0;

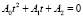
3) решив квадратное уравнение получить корни t1, t2;

4) проверить условие t > 0;

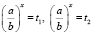
5) решить уравнения

Пример. Решим уравнение

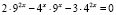
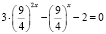
1) ;

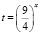
2) обозначим , t > 0;

3) получим квадратное уравнение

, ;

4) t2, не удовлетворяет условию t > 0;

5) . Ответ: .

Общие рекомендации по методике обучения школьников решению уравнений

На основе анализа теоретико-методических основ изучения уравнений в школьном курсе сформулируем этапы обучения школьников решению уравнений [5–6].

1. Вводится определение конкретного вида уравнений.

2. Решаются простейшие уравнения данного вида.

3. Анализируются действия, необходимые для их решения.

4. Выводится алгоритм решения простейших уравнений.

5. Решаются несложные уравнения данного вида, не являющиеся простейшими.

6. Анализируются действия, необходимые для их решения.

7. Применяются общие методы решения уравнений к данному виду уравнений.

8. Выводится алгоритм решения данного вида уравнений общими методами решения уравнений.

9. Формулируются частные методы решения уравнений, которые подходят только к данному виду уравнений.

10. Выводится алгоритм решения уравнений частными методами.

11. Анализируются полученные частные приемы, выделяются в их составе общие действия.

12. Формулируется обобщенный прием решения уравнений.

Выводы

Чтобы формировать умения решать уравнения, необходимо обучать способам решения уравнений. Каждый способ решения уравнений состоит из отдельных действий, следовательно нужно формировать умения у школьников выполнять действия, адекватные поиску способа решения и решению уравнения. На основе анализа теоретико-методических основ изучения уравнений в школьном курсе нами были сформулированы этапы обучения школьников решению уравнений.

5 класс. Изучение понятий уравнения, корня уравнений, что значит решить уравнение. Решение наряду с простыми уравнениями, более сложных, содержащих неизвестное в одной части уравнения.

6 класс. Решение уравнений, содержащих переменную в обеих частях уравнения. Для этого изучается правило переноса слагаемых из одной части уравнения в другую. Применение уравнений к решению текстовых задач.

Систематическое изучение алгебраических уравнений и неравенств (7 – 9 классы)

7 класс. Понятие уравнения с одной и двумя переменными. Изучение понятия и свойств равносильных уравнений. Решение линейных уравнений, систем двух линейных уравнений с двумя переменными, применение уравнений и систем уравнений первой степени к решению текстовых задач.

9 класс. Понятие дробно-рационального уравнения, его решение и применение к решению текстовых задач. Методы решения уравнений: разложение на множители, метод введения новой переменной.

Тема “Уравнения и неравенства” является одной из самых основных тем школьного курса математики. Она имеет большое внутрипредметное и межпредметное значение. Внутрипредметные связи: тема связана с темой “Функции” и темой “Тождественные преобразования”. Межпредметные связи: тема широко используется в физике и химии. Основная задача темы – освоить способы решения различных видов уравнений и неравенств.

Основными понятиями темы являются:

уравнение, неравенство;
корень уравнения, решение неравенства;
равносильность уравнений, равносильность неравенств.

Понятие уравнение рассматривается дважды: в 5 классе, как равенство, содержащее неизвестное, (здесь понятие вводится конкретно-индуктивным методом через решение задачи, используя картинку с весами) и в 7 классе, где вводится уже точное определение уравнения: уравнение – это равенство, содержащее переменную. Здесь же вводятся понятия “корень уравнения” и “решить уравнение”. В 7 классе вводится и понятие “равносильные уравнения”, формулируются теоремы о равносильных преобразованиях. Эти теоремы формулируются в виде свойств, они не доказываются, а поясняются на примерах.

С числовыми неравенствами 2 5 учащиеся знакомятся в начальной школе. В 5 классе вводится двойное неравенство: 1 , ?, ? называется неравенством.

Понятие “решение неравенства” удобно вводить по аналогии с понятием “корень уравнения”.

А можно ли указать все решения неравенства? Встает вопрос, как изобразить все решения неравенства? Учитель сообщает, что оказывается, решения неравенства изображаются на координатной прямой, а ответ записывается с помощью числовых прямых. После этого необходимо рассмотреть всевозможные случаи неравенств и их решений.

При обучении решению любого вида уравнений и неравенств строго соблюдается методика формирования математических умений. Например, в 5 классе решаются линейные уравнения, которые содержат переменную только в одной части. Записывается на доске уравнение: 52 + (3x – 14) = 62. Что представляет собой левая часть уравнения? Сумма. Назовите слагаемые. Какое слагаемое известно? В каком из компонентов содержится неизвестное? Как найти неизвестное слагаемое? 3x – 14 = 10. Что представляет собой левая часть уравнения? Разность. В каком из компонентов содержится неизвестное? Как найти уменьшаемое? 3x = 24. Что представляет собой левая часть уравнения? Произведение. Назовите множители. Какой множитель известен? В каком из компонентов содержится неизвестное? Как найти неизвестный множитель? x = 8. Как проверить, что число 8 является корнем уравнения? 52 + (3 ? 8 – 14) = 62 ? 62 = 62. После этого составляем и записываем в тетрадь правило решения таких уравнений:

определяем вид уравнения по последнему действию;
определить, что неизвестно и найти неизвестное по соответствующему правилу;
в случае необходимости, повторит шаги 1 – 2;
найти корень уравнения;
выполнить проверку;
записать ответ.

Учитель показывает образец решения на доске. После этого переходим к решению упражнений на отработку каждого шага правила.

Читайте также: