Методика изучения теорем в школьном курсе математики

Обновлено: 07.07.2024

В математике каждое утверждение, справедливость которого устанавливается путём рассуждений, называется теоремой. Во всякой теореме можно выделить разъяснительную часть, условие и заключение. Итак, структуру теоремы представляем следующим образом: PI "если А, то В", где P означает разъяснительную часть, А - условие, а В - заключение теоремы.

1) Из А следует Б. (a=>b) -прямое утверждение.

2) Из Б следует А. (b=>a) - обратное утверждение .

3) Из не А следует не Б. ( ) противоположное утверждение.

4) Из не Б следует не А. ( ) контрапозитивное утверждение.

Если импликация P=>Q является теоремой, то : условие P называется достаточным условием для условия Q, а условие Q – необходимым условием для условия P.

Если теоремами являются импликации P => Q и Q=> P, то каждое из условий является необходимым и достаточным для другого.

Этапы работы с теоремой в школе

Профессиональный – выполнение логико-математического анализа, выбор методов работы, отбор содержания;

Подготовительный – актуализация необходимых знаний учащихся, мотивация необходимости изучения факта;

Введение формулировки теоремы и осуществление ее доказательства - первичное усвоение факта и его доказательства учащимися;

Применение теоремы в качестве аргумента при выводе следствий.

Этапы изучения теоремы учащимися

Мотивация изучения, Ознакомление с фактом, отраженным в теореме, Формулировка теоремы,

Усвоение содержания теоремы, ее структуры. Ознакомление со способом доказательства,

Доказательство теоремы, Применение теоремы, Установление связи с другими теоремами

Методы введения теоремы

Система задач на усвоение теоремы и ее доказательства

На раскрытие необходимости знания математического факта, сформулированного в теореме;

На актуализацию фактов, используемых при доказательств и способов доказательств, аналогичных используемым для данной теоремы;

На осознание факта, сформулированного в теореме;

На усвоение формулировки;

На усвоение отдельных этапов доказательства;

На повторение хода доказательства (например, на других чертежах);

На отыскание другого способа доказательства;

На применение теоремы для получения новых математических фактов (следствий);

На применение теоремы для решения других задач на вычисление, построение и доказательства.

Виды формулировок теорем: категорическая и условная (импликативная).

Структура формулировки: условие, заключение, разъяснительная часть.

Логическая структура условия и заключения: конъюнктивная, дизъюнктивная.

1. Теорема "Если диагонали параллелограмма взаимно перпендикулярны или делят его углы пополам, то этот параллелограмм - ромб" имеет структуру А V В => C, где А - "диагонали параллелограмма взаимно перпендикулярны"; В - "(диагонали параллелограмма) делят его углы пополам"; С - "этот параллелограмм - ромб".

2. Теорема о средней линии трапеции имеет структуру: А => В & С, где А - "четырехугольник - трапеция"; В - "его средняя линия параллельна основаниям"; С - "(его средняя линия) равна полусумме оснований".

Часто в формулировках теорем используется выражение "необходимо и достаточно" (ПРИЗНАК). В логике это выражение соответствует эквиваленции, которая, как известно, представима в виде конъюнкции двух импликаций. Одна из этих импликаций выражает теорему, доказывающую НЕОБХОДИМОСТЬ признака, другая выражает теорему, доказывающую ДОСТАТОЧНОСТЬ признака. Например, признак перпендикулярности двух плоскостей:

"Для того чтобы две плоскости были перпендикулярны, НЕОБХОДИМО и ДОСТАТОЧНО, чтобы одна из них проходила через прямую, перпендикулярную к другой", может быть сформулирован и так: "Две плоскости перпендикулярны, ЕСЛИ И ТОЛЬКО ЕСЛИ одна из них проходит через прямую, перпендикулярную к другой":

Опытные педагоги сходятся во мнении, что готовить учеников к доказательству математических утверждений целесообразно начинать заранее. Где-то с 4-5 класса следует развивать у детей умения оперировать понятиями, работать с текстом, рисунками, схемами, выбирать из них необходимые данные для объяснения тех или иных утверждений. Эти навыки пригодятся, поскольку построение доказательств базируется именно на них.

Приемы и методы доказательства теорем

Перед учителем стоит задача: обеспечить сознательное усвоение математических знаний, воспитать навыки самостоятельной мыслительной деятельности, умение рационально применять полученные знания. Этого можно достичь лишь при успешном выборе учителем приемов и методов обучения доказательству математических утверждений. Если изучение теорем сводить лишь к применению самого содержания без доказательств, то теряется весь смысл математического образования, которое заключается в развитии аналитического и логического мышления.

Учителю, для того, чтобы подготовиться к подаче и доказательству утверждения, следует четко спланировать порядок изложения материала при изучении теоремы. А этапы изучения таковы:

мотивация изучения теоремы (необходимость перевода на математический язык наблюдаемых в жизни явлений и процессов);
знакомство с содержанием;
обоснование необходимости доказать теорему;
выполнение рисунка (для наглядности) и краткая запись содержания теоремы;
поиск приемов доказательства, собственно доказательство и его математическая интерпретация;
закрепление;
примеры применения теоремы.

В зависимости от сложности материала, доказательство можно проводить:

только учителю с последующим проговариванием по частям (задать такие вопросы: что было дано, что следовало доказать, как формулируется теорема, с чего начали доказательство, что делали, какие теоремы или аксиомы использовались при доказательстве и для чего);
учителю совместно с учениками;
ученикам по предложенному учителем алгоритму (докажите теорему самостоятельно, сравните свое доказательство с тем, что приведено в учебнике, проанализируйте расхождения).

Приучать школьников к самостоятельному доказательству утверждений можно только после соответствующей подготовки и знакомства с методами и приемами, которые используются с такой целью в математике.

По определению доказательство — это рассуждение, цель которого заключается в обосновании (или опровержении) истинности какого-либо утверждения.

Элементы доказательства

тезис (математическое утверждение, которое надо доказывать)

аргументы (положения, на которых строится доказательство)

демонстрация (логическое обоснование взаимосвязи вышеуказанных элементов, результат — переход от аргументов к начальному тезису)

1 Теоремы и методика их изучения в школьном курсе математики ТМОМ Методические основы обучения математике

3 Сведения из логики Доказательством называют конечную последовательность предложений данной теории, каждое из которых либо является аксиомой, либо выводится из одного или нескольких предыдущих предложений этой теории по правилам логического вывода. Теорема – предложение, которое является последним в каком - либо доказательстве

4 Правила вывода X Y, X - правило заключения Y X Y, Y - правило отрицания X X Y - правило контрапозиции Y X X Y Z - правило расширенной контрапозиции X Z Y X Y, Y Z - правило силлогизма X Z

5 Структура доказательства Тезис – суждение, истинность которого доказывается. Аргументы доказательства – суждения, истинность которых установлена и из которых необходимо следует истинность доказываемого тезиса (определения понятий, аксиомы, постулаты, теоремы, общие законы науки). Демонстрация – логический процесс взаимосвязи суждений, при котором осуществляется переход от аргументов к тезису.

6 Требования к элементам доказательства Тезис: сформулирован ясно, точно, определенно и непротиворечиво; остается неизменным на протяжении всего доказательства или заменяется только равносильным суждением; не должен находиться в противоречии с доказанными ранее суждениями. Аргументы: аргумент должен быть истинным; истинность аргумента должна быть доказана независимо от тезиса; аргументы должны быть непротиворечивыми. Демонстрация: полнота демонстрации; построение по правилам вывода.

7 Формулировки теорем Виды формулировок : категорическая; условная (импликативная). Структура формулировки: условие; заключение; разъяснительная часть. Логическая структура условия и заключения: конъюнктивная; дизъюнктивная.

8 Виды теорем P Q - прямое утверждение (теорема), Q P - обратное утверждение (теорема), P Q - противоположное утверждение(теорема), Q P - контрапозитивное утверждение (теорема) P Q и Q P - пары равносильных Q P и P Q утверждений (теорем)

9 Если импликация P Q является теоремой, то : условие P называется достаточным условием для условия Q, а условие Q – необходимым условием для условия P. Если теоремами являются импликации P Q и Q P, то каждое из условий является необходимым и достаточным для другого.

11 Логико-математический анализ теоремы Логический анализ - раскрытие логической структуры предложения, вида суждения и способа его конструирования; Математический анализ - раскрытие математического содержания выделенных элементов структуры. Логико-математический анализ предполагает: установление формы формулировки; определение вида суждения; перевод формулировки, если необходимо, в импликативную форму; запись структуры теоремы, т.е. вычленение разъяснительной части, условия, заключения с выделением простых высказываний и логических связок; формулирование обратного утверждения и определение его истинности.

12 Теорема о свойстве смежных углов: Сумма смежных углов равна 180 градусам сформулирована в категоричной форме; вид суждения – простое, общеутвердительное; импликативная форма: если любые два угла смежные, то их сумма равна 180 градусам; разъяснительная часть: множество углов; условие: углы смежные; заключение: сумма углов равна 180 градусам; обратное утверждение: если сумма двух углов равна 180 градусам, то они смежные, - теоремой не является.

13 Этапы работы с теоремой профессиональный – выполнение логико- математического анализа, выбор методов работы, отбор содержания; подготовительный – актуализация необходимых знаний учащихся, мотивация необходимости изучения факта; введение формулировки теоремы и осуществление ее доказательства - первичное усвоение факта и его доказательства учащимися; применение теоремы в качестве аргумента при выводе следствий.

14 Этапы изучения теоремы учащимися (по Г.И. Саранцеву) 1.Мотивация изучения. 2.Ознакомление с фактом, отраженным в теореме. 3.Формулировка теоремы. 4.Усвоение содержания теоремы, ее структуры. 5.Ознакомление со способом доказательства. 6.Доказательство теоремы. 7.Применение теоремы. 8.Установление связи с другими теоремами.

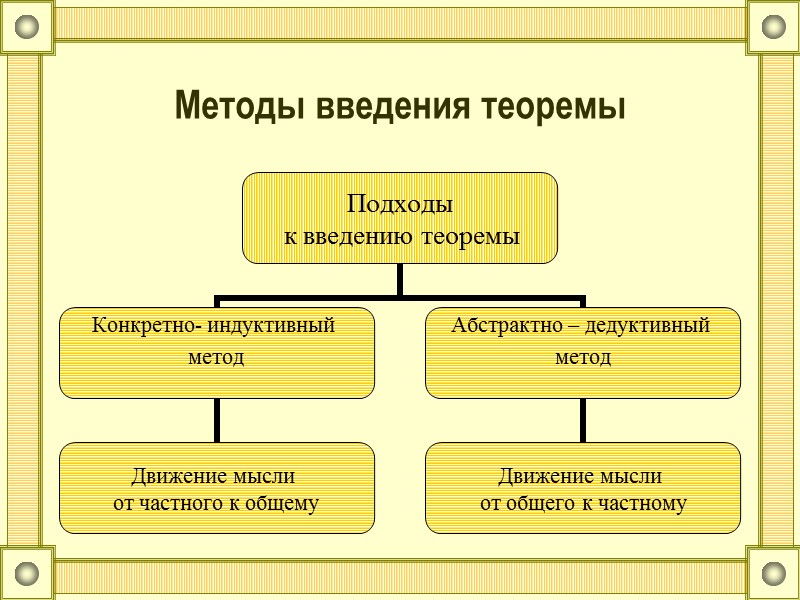
15 Методы введения теоремы Подходы к введению теоремы Конкретно- индуктивный метод Движение мысли от частного к общему Абстрактно – дедуктивный метод Движение мысли от общего к частному

17 Приемы поиска прямого доказательства Преобразование условий (синтетический) Суть приема в доказательстве того, что заключение необходимо для условия доказываемого предложения, Схема рассуждений: P P 1 P 2 … P n Q Преобразование заключения Восходящий анализ Суть приема в доказательстве того, что условие теоремы достаточно для ее заключения, Схема рассуждения: P P n … P 2 P 1 Q Нисходящий анализ Суть приема в установлении факта, что условие необходимо для заключения, с последующим обращением цепочки рассуждений, Схема рассуждения: Q Q 1 Q 2 … Q n P и Q Q 1 Q 2 … Q n P

18 Прием аналитико-синтетического поиска доказательства Разворачиваются условия: на основе ранее изученных определений и теорем выводятся следствия ( А А 1 А 2 … ) Расширенный список свойств сравнивается с заключением Отыскивается совокупности свойств, достаточные для заключения ( … В 2 В 1 В) Отбирается одна из совокупностей свойств достаточных для доказательства (определение или признак понятия).

19 Выводятся следствия из ранее найденных следствий, достаточных по отношению одному из свойств, входящих в совокупность достаточных для заключения свойств Замыкание цепочек, идущих от условия и ведущих к заключению Схема рассуждений: А А 1 А 2 … А n В n … В 2 В 1 В Прием аналитико-синтетического поиска доказательства

21 Формы представления доказательства Цепочки рассуждений Схема действий: 1.Указывается большая посылка (истинное предложение теории). 2.Указывается малая посылка (частное свойство рассматриваемых объектов или условие тезиса). 3.Делается вывод на основе правила заключения или правила отрицания. Цепочки истинных предложений Схема действий: 1.Указывается некоторое частное истинное утверждение. 2.Указывается положение, обосновывающее истинность частного суждения (положение теории или частное условие тезиса теоремы).

22 Система задач на усвоение теоремы и ее доказательства на раскрытие необходимости знания математического факта, сформулированного в теореме; на актуализацию фактов, используемых при доказательств и способов доказательств, аналогичных используемым для данной теоремы; на осознание факта, сформулированного в теореме; на усвоение формулировки; на усвоение отдельных этапов доказательства;

23 на повторение хода доказательства (например, на других чертежах); на отыскание другого способа доказательства; на применение теоремы для получения новых математических фактов (следствий); на применение теоремы для решения других задач на вычисление, построение и доказательства. Система задач на усвоение теоремы и ее доказательства

24 Уровни обучения доказательствам (по Г.И. Саранцеву) 5 -6 класс формирование потребности в логических доказательствах; формирование умения осуществлять дедуктивные выводы; 6 -7 класс обучение эвристическим приемам и их применению; обучение выполнению цепочки логических шагов; 7 класс обучение самостоятельному разбору готового доказательства; формирование умения выделять идею доказательства; 7 – 8 класс обучение использования методов научного познания; привлечение к самостоятельному доказательству; 9 класс обучение умению опровергать предложенные доказательства.

Теоремы и методики их изучения в школьном курсе математики ТМОМ Методические основы обучения математике Тема 4

Сведения из логики Доказательством называют конечную последовательность предложений данной теории, каждое из которых либо является аксиомой, либо выводится из одного или нескольких предыдущих предложений этой теории по правилам логического вывода. Теорема – предложение, которое является последним в каком - либо доказательстве

Правила вывода X Y, X - правило заключения Y X Y, Y - правило отрицания X X Y - правило контрапозиции Y X X Y Z - правило расширенной контрапозиции X Z Y X Y, Y Z - правило силлогизма X Z

Структура доказательства Тезис – суждение, истинность которого доказывается. Аргументы доказательства – суждения, истинность которых установлена и из которых необходимо следует истинность доказываемого тезиса (определения понятий, аксиомы, постулаты, теоремы, общие законы науки). Демонстрация – логический процесс взаимосвязи суждений, при котором осуществляется переход от аргументов к тезису.

Требования к элементам доказательства Тезис: сформулирован ясно, точно, определенно и непротиворечиво; остается неизменным на протяжении всего доказательства или заменяется только равносильным суждением; не должен находиться в противоречии с доказанными ранее суждениями. Аргументы: аргумент должен быть истинным; истинность аргумента должна быть доказана независимо от тезиса; аргументы должны быть непротиворечивыми. Демонстрация: полнота демонстрации; построение по правилам вывода.

Формулировки теорем Виды формулировок : категорическая; условная (импликативная). Структура формулировки: условие; заключение; разъяснительная часть. Логическая структура условия и заключения: конъюнктивная; дизъюнктивная.

Виды теорем P Q - прямое утверждение (теорема), Q P - обратное утверждение (теорема), P Q - противоположное утверждение(теорема), Q P - контрапозитивное утверждение (теорема) P Q и Q P - пары равносильных Q P и P Q утверждений (теорем)

Если импликация P Q является теоремой, то : условие P называется достаточным условием для условия Q, а условие Q – необходимым условием для условия P. Если теоремами являются импликации P Q и Q P, то каждое из условий является необходимым и достаточным для другого.

Методы доказательства теорем Метод доказательства – способ связи аргументов при переходе от условия к заключению

Логико-математический анализ теоремы Логический анализ - раскрытие логической структуры предложения, вида суждения и способа его конструирования; Математический анализ - раскрытие математического содержания выделенных элементов структуры. Логико-математический анализ предполагает: установление формы формулировки; определение вида суждения; перевод формулировки, если необходимо, в импликативную форму; запись структуры теоремы, т.е. вычленение разъяснительной части, условия, заключения с выделением простых высказываний и логических связок; формулирование обратного утверждения и определение его истинности.

Теорема о свойстве смежных углов: Сумма смежных углов равна 180 градусам сформулирована в категоричной форме; вид суждения – простое, общеутвердительное; импликативная форма: если любые два угла смежные, то их сумма равна 180 градусам; разъяснительная часть: множество углов; условие: углы смежные; заключение: сумма углов равна 180 градусам; обратное утверждение: если сумма двух углов равна 180 градусам, то они смежные, - теоремой не является.

Этапы работы с теоремой профессиональный – выполнение логико-математического анализа, выбор методов работы, отбор содержания; подготовительный – актуализация необходимых знаний учащихся, мотивация необходимости изучения факта; введение формулировки теоремы и осуществление ее доказательства - первичное усвоение факта и его доказательства учащимися; применение теоремы в качестве аргумента при выводе следствий.

Этапы изучения теоремы учащимися (по Г.И. Саранцеву) Мотивация изучения. Ознакомление с фактом, отраженным в теореме. Формулировка теоремы. Усвоение содержания теоремы, ее структуры. Ознакомление со способом доказательства. Доказательство теоремы. Применение теоремы. Установление связи с другими теоремами.

Методы введения теоремы

Приемы поиска прямого доказательства Преобразование условий (синтетический) Суть приема в доказательстве того, что заключение необходимо для условия доказываемого предложения, Схема рассуждений: P P1 P2 … Pn Q Преобразование заключения Восходящий анализ Суть приема в доказательстве того, что условие теоремы достаточно для ее заключения, Схема рассуждения: P Pn … P 2 P1 Q Нисходящий анализ Суть приема в установлении факта, что условие необходимо для заключения, с последующим обращением цепочки рассуждений, Схема рассуждения: Q Q1 Q2 … Qn P и Q Q1 Q2 … Qn P

Прием аналитико-синтетического поиска доказательства Разворачиваются условия: на основе ранее изученных определений и теорем выводятся следствия ( А А1 А2 … ) Расширенный список свойств сравнивается с заключением Отыскивается совокупности свойств, достаточные для заключения ( … В2 В1 В) Отбирается одна из совокупностей свойств достаточных для доказательства (определение или признак понятия).

Выводятся следствия из ранее найденных следствий, достаточных по отношению одному из свойств, входящих в совокупность достаточных для заключения свойств Замыкание цепочек, идущих от условия и ведущих к заключению Схема рассуждений: А А1 А2 … Аn Вn … В2 В1 В Прием аналитико-синтетического поиска доказательства

Формы представления доказательства Цепочки рассуждений Схема действий: Указывается большая посылка (истинное предложение теории). Указывается малая посылка (частное свойство рассматриваемых объектов или условие тезиса). Делается вывод на основе правила заключения или правила отрицания. Цепочки истинных предложений Схема действий: Указывается некоторое частное истинное утверждение. Указывается положение, обосновывающее истинность частного суждения (положение теории или частное условие тезиса теоремы) .

Система задач на усвоение теоремы и ее доказательства на раскрытие необходимости знания математического факта, сформулированного в теореме; на актуализацию фактов, используемых при доказательств и способов доказательств, аналогичных используемым для данной теоремы; на осознание факта, сформулированного в теореме; на усвоение формулировки; на усвоение отдельных этапов доказательства;

на повторение хода доказательства (например, на других чертежах); на отыскание другого способа доказательства; на применение теоремы для получения новых математических фактов (следствий); на применение теоремы для решения других задач на вычисление, построение и доказательства. Система задач на усвоение теоремы и ее доказательства

Уровни обучения доказательствам (по Г.И. Саранцеву) 5 -6 класс формирование потребности в логических доказательствах; формирование умения осуществлять дедуктивные выводы; 6 -7 класс обучение эвристическим приемам и их применению; обучение выполнению цепочки логических шагов; 7 класс обучение самостоятельному разбору готового доказательства; формирование умения выделять идею доказательства; 7 – 8 класс обучение использования методов научного познания; привлечение к самостоятельному доказательству; 9 класс обучение умению опровергать предложенные доказательства.

Темы практических заданий и список литературы по теме Можно посмотреть здесь

Благодарю за внимание!

Всегда можно из одного вида формулирования теоремы перейти в другой. Если теорема сформулирована в условной форме, то в ней должно быть ясно указан при каких условиях рассматривается в ней тот или иной объект (условие) и что в этом объекте утверждается (заключение теоремы).

Теорема: В параллелограмме диагонали, пересекаясь, делятся пополам.

Если четырехугольник – параллелограмм, то…

Условие Р четырехугольник – параллелограмм, диагонали его пересекаются

ЗаключениеG точка пересечения диагоналей делит каждую из них пополам.

Доказательство теоремы состоит в том, чтобы показать, что если выполняется условие, то из него логически следует заключение, т.е., приняв, что Р истинно, соответствии с правилами вывода показать, что G истинно, и тем самым получить возможность утвердить, что данное высказывание (теорема) истинно целом.

Доказательство включает в себя три основных элемента:

Тезис (Главная цель доказательства – установить истинность тезиса). Форма выражения тезиса суждение.

Аргументы(основание) доказательства – положения на которые опирается доказательство и из которых при условии их истинности необходимо следует истинность доказываемого тезиса. Форма выражения аргументов - суждения. Связывая аргументы, приходим к умозаключению, которые строятся по определенным правилам. Аргументы, на которые можно опереться при доказательстве: аксиомы, определения, ранее доказанные теоремы.

Демонстрация– логический процесс взаимосвязи суждений, в результате которого осуществляется переход от аргументов к тезису.

При изучении теорем школьного курса математики учитель придерживается следующей последовательности:

1. Постановка вопроса (создание проблемной ситуации)

2. Обращение к опыту учащихся

3. Высказывание предположения

4. Поиск возможных путей решения

5. Доказательство найденного факта

6. Проведение доказательства в максимальной форме

7. Установление зависимости доказанной теоремы от ранее известных.

Процесс изучения школьниками теоремы включает этапы:

1. Мотивация изучения теоремы

2. Ознакомление с фактом, отраженным в теореме

3. Формулировка теоремы и выяснение смысла каждого слова в формулировке теоремы

4. Усвоение содержания теоремы

5. Запоминание формулировки теоремы

6.Ознакомление со способом доказательства

9.Установление связей теоремы с ранее изученными теоремами

Этапы изучение теоремы

1. Раскрытие ее содержания (формулировка теоремы)

Работа над структурой
Построение чертежа, краткая запись содержания теоремы
Поиск доказательства, доказательство и ее запись
Закрепление теоремы
Применение теоремы

Теорема– это мат - ое предложение, истинность которого устанавливается посредством доказательства (рассуждения)

Вида формулирования теоремы