Методика изучения иррациональных чисел в основной школе

Обновлено: 05.07.2024

2. Дайте определение иррационального числа. Приведите примеры иррациональных чисел.

3. Укажите причины расширения множества рациональных чисел.

4. Что обозначает ?

5. Дайте определение арифметического квадратного корня.

6. Выберите верное утверждение: ; ; ; ; ; .

7. Какая точка на координатной прямой соответствует числу ?

8. Опишите процесс измерения длины отрезка? Что является результатом измерения?

9. Какие отрезки называются несоизмеримыми? Приведите примеры несоизмеримых отрезков?

10. Как, согласно легенде, боги покарали ученика Пифагора, который разгласил тайну о несоизмеримости стороны и диагонали квадрата?

11. Постройте отрезок длиной .

12. Докажите, что – иррациональное число.

13. Упростите выражение .

14. Вычислите с точностью до сотых .

15. Проанализируйте достоинства и недостатки методики изучения иррациональных чисел до изучения действительных чисел, после изучения действительных чисел.

16. Проанализируйте достоинства и недостатки методики изучения арифметического квадратного корня до изучения иррациональных чисел, после изучения иррациональных чисел.

Разработать фрагмент урока:

· по введению операции извлечения корня из произведения, степени, частного;

· по введению операции сравнения иррациональных чисел.

Темы презентаций (5-7 минут):

1. Старинные системы записи чисел.

2. Римские цифры.

3. Вавилонская система исчисления.

4. Позиционные системы исчисления (шестидесятеричная, двоичная, десятеричная).

5. Какие числа называют числами-близнецами?

6. Названия больших чисел.

7. Старинные вычислительные приборы.

8. Из истории умножения и деления.

9. Признаки делимости чисел.

10. История отрицательных чисел.

11. О бедном проценте замолвите слово.

12. Простые числа.

13. Совершенные и дружественные числа.

14. Незнакомые обыкновенные дроби.

15. Десятичные дроби.

17. Цепные дроби.

18. Числа Фидия и золотое сечение.

19. Трансцендентные числа.

22. Зачем нужны комплексные числа?

Использовать:

2) Депман И.Я., Виленкин Н.Я. За страницами учебника математики: Пособие для учащихся 5-6 кл. сред. шк. – М.: Просвещение, 1989.

Лабораторная работа № 4

Актуализация знаний:

1. Дайте определение рационального числа.

2. Дайте определение иррационального числа. Приведите примеры иррациональных чисел.

3. Укажите причины расширения множества рациональных чисел.

4. Что обозначает ?

5. Дайте определение арифметического квадратного корня.

6. Выберите верное утверждение: ; ; ; ; ; .

7. Какая точка на координатной прямой соответствует числу ?

8. Опишите процесс измерения длины отрезка? Что является результатом измерения?

9. Какие отрезки называются несоизмеримыми? Приведите примеры несоизмеримых отрезков?

11. Постройте отрезок длиной .

12. Докажите, что – иррациональное число.

13. Упростите выражение .

14. Вычислите с точностью до сотых .

Разработать фрагмент урока:

· по введению операции извлечения корня из произведения, степени, частного;

· по введению операции сравнения иррациональных чисел.

Темы презентаций (5-7 минут):

1. Старинные системы записи чисел.

2. Римские цифры.

3. Вавилонская система исчисления.

4. Позиционные системы исчисления (шестидесятеричная, двоичная, десятеричная).

5. Какие числа называют числами-близнецами?

6. Названия больших чисел.

7. Старинные вычислительные приборы.

8. Из истории умножения и деления.

9. Признаки делимости чисел.

10. История отрицательных чисел.

11. О бедном проценте замолвите слово.

12. Простые числа.

13. Совершенные и дружественные числа.

14. Незнакомые обыкновенные дроби.

15. Десятичные дроби.

17. Цепные дроби.

18. Числа Фидия и золотое сечение.

19. Трансцендентные числа.

22. Зачем нужны комплексные числа?

Использовать:

Лабораторная работа № 4

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.

Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.

1.1. Краткий обзор развития понятия иррационального числа …………..

1.2. Действительные числа как десятичные дроби ………………………

1.3. Действительные числа как цепные дроби ……………………………

Глава 2. Методика изучения иррациональных чисел в школе …

2.1.Методика расширения числовых множеств в курсе алгебры средней школы ………………………………………………………………………………

2.3. Анализ школьных учебников по алгебре ……………………………

2.4. Система упражнений в разрезе классов ……………………………….

Глава 3. Педагогический эксперимент и его результаты ……….

3.2. Ход эксперимента и его результаты ………….…………………….….

3.3. Фрагменты конспектов уроков …………………….….…………….

Вложение	Размер
gotovaya_bayazovoy_2.doc	1.84 МБ

Предварительный просмотр:

По теме: методические разработки, презентации и конспекты

Тестирование в школьном курсе математики и на элективных курсах как средство повышения качества обучения.

Описание педагогического опыта работы.Тестирование в школьном курсе математики и на элективных курсах как средство повышения качества обучения.

Программа курса по выбору для учащихся 9 кл. "Способы и методы решения нестандартных задач школьного курса математики"

Данная программа для учащихся 9 класса относится к группе занятий в системе дополнительного образования, которые предназначены как для дополнения знаний учащихся, полученных ими на уроках, так и для и.

простые программы из школьного курса математики на языке PascalABC Разложение числа на простые множители

Программа на языке программирования PascalABC для получения разложения на простые множители.

Элективный курс по теме "Повторяем и систематизируем школьный курс математики"

Данный элективный курс помогает подготовить учащихся к успкшной сдаче ЕГЭ.

Методологические основы построения содержания школьного курса математики. Возможности содержания темы школьного курса математики в реализации Программы развития УУД в ООО

Логико-дидактический анализ понятий и теорем темы «Сложение и вычитание натуральных чисел».

в курсе алгебры средней школы
Первое расширение понятия о числе, которое учащиеся усваивают после ознакомления с натуральными числами – это добавление нуля. Сначала 0 – знак для обозначения отсутствия числа. Почему же нельзя делить на нуль?

Разделить – значит найти . Два случая: 1) , следовательно, надо найти Например, система натуральных чисел не является числовым полем; система целых чисел тоже не числовое поле. Система рациональных чисел – числовое поле.

Возможны и такие варианты:

Элементарное понятие о дробном числе дается уже в начальной школе как о нескольких долях единицы.

Появление нового числового множества сопровождается введением правил сравнения (равенства и неравенства) чисел и арифметических операций над ними. Средством обоснования правил сравнения нередко служит координатная прямая.

Получив числовое поле, дальнейшее расширение уже не может быть продиктовано невыполнением действий. Расширение понятия числа было вызвано геометрическими соображениями, а именно: отсутствием взаимно однозначного соответствия между множеством рациональных чисел и множеством точек числовой прямой. Для геометрии необходимо, чтобы каждая точка числовой прямой имела абсциссу, т. е. чтобы каждому отрезку при данной единице измерения соответствовало число, которое можно было бы принять за его длину. Эта цель достигается после того, как поле рациональных чисел (с помощью присоединения к нему системы иррациональных чисел) подвергается расширению до системы действительных чисел, которая является числовым полем.

К необходимости этого расширения приводит и невозможность извлечения корня из положительного, нахождения логарифма положительного числа при положительном основании.

Интуитивные представления учащихся естественны, так как практически нельзя обнаружить существование несоизмеримых отрезков. Не надо строить строгую теорию, достаточно создать верные представления о сущности вопроса.

В большинстве учебников иррациональное число рассматривается как бесконечная непериодическая десятичная дробь (как и в теории Вейерштрасса). В некоторых учебниках – длина отрезка, несоизмеримого с единицей масштаба, а затем показывается, как находится приближения этого числа в виде десятичных дробей.

Далее необходимо установить, что существует взаимно однозначное соответствие между множеством действительных чисел. Поскольку иррациональные числа вводятся для измерения отрезков, несоизмеримых с единицей длины, то сразу получается, что для каждого отрезка можно найти действительное число, выражающее его отношение к единице длины. Обратное положение есть аксиома непрерывности прямой. В большинстве учебников не формулируется, а подчеркивается это взаимно однозначное соответствие. В некоторых учебниках (Д. К. Фадеева и др.) используется подход Кантора: для всякой стягивающейся последовательности вложенных друг в друга промежутков на прямой существует точка, принадлежащая всем промежуткам последовательности. Отсюда и следует непрерывность множества действительных чисел.

Можно не доказывать непрерывность множества R, но необходимо выяснить различие в структуре множеств рациональных и действительных чисел. Множество рациональных чисел плотно (между любыми двумя рациональными числами существует сколько угодно рациональных чисел), но не непрерывно. Множество разрывов имеет большую мощность.

Н. Н. Лузин предложил такое сравнение: если представить, что рациональные точки не пропускают солнечные лучи, и поставить прямую на пути лучей, то нам покажется, что солнце пробивается почти сплошь. У С. И. Туманова: рациональные числа окрашены в черный цвет, а иррациональные – в красный. Тогда прямая представлялась бы сплошь красной. О мощности множества иррациональных чисел можно судить через рассмотрение их как полученных из рациональных разрушением периода бесконечной десятичной дроби, так как для каждого рационального числа можно предложить множество иррациональных.

Геометрическое построение иррациональных чисел с использованием теоремы Пифагора приводится на рис. 2.

Из всех теорий иррациональных чисел более доступной считалась теория Кантора–Мере, рассматривающая стягивающиеся последовательности вложенных в друг друга сегментов. Поэтому во многих учебниках результат действий над иррациональными числами рассматривается как число, заключенное между всеми приближенными результатами, взятыми по избытку, и всеми приближенными значениями, взятыми по недостатку. Такое определение не создает у учащихся представления о результате действий над иррациональными числами вообще об иррациональном числе. В экспериментах В. К. Матушка (контрольная работа среди лучших учеников) школьники считают иррациональные числа неточными, колеблющимися, приближенными. Многие считают, что числа
Следует обратить внимание учащихся, что в результате действий над иррациональными числами могут получиться как рациональные, так и иррациональные. Для этого нужно предложить примеры на сложение непериодических дробей.

Разъясняя точный смысл вводимых терминов и привлекая достаточное количество геометрических иллюстраций, можно обеспечить сознательное усвоение перечисленных в этих четырех пунктах математических фактов, причем некоторые высказанные предложения доказываются, другие применяются без доказательства, но с проверкой на частных примерах.

1. Введение начинается с целесообразно подобранной задачи. Например: извлечение квадратного корня из положительного числа, не являющегося полным квадратом; каким числом выражается длина диагонали квадрата со стороной 1; чему равна сторона квадрата, если известно, что его площадь равна 3.

Практические задачи: задачи измерения; каждой ли точке координатной прямой соответствует рац число?

Изображение чисел на координатной прямой

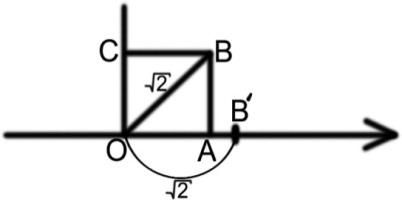
П окажем, что т. В’ соответствует числу, не явл рацион, т. к. диагональ квадрата ОВ несоизмерима с его стороной ОА

Д-во, что т. В не соотв. никакому рац числу

Т. к. т. В’ находится на ОХ,

От противного: пусть – несократимая дробь. Обе части – неотрицательны, возведем в квадрат, получим: , , => – четное, => – четное. Значит можно представить в виде . Подставим в :

=> , => – четное, – четное. Тогда имеем – четные. Это противоречит тому, что – несократимая дробь. => => не является рациональным числом.Таким образом, число можно изобразить на координатной прямой некоторым числом, которое не является рациональным. Такие числа называются иррациональными.

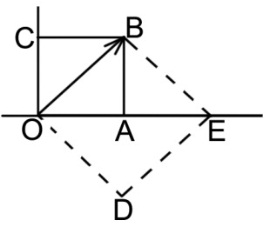
С другой стороны .

Если натуральное число не есть квадрат некоторого натурального числа, то оно есть квадрат иррационального числа. Таким образом, – иррациональное число.

Иррациональные числа – есть бесконечные десятичные непериодические дроби. Так как нельзя извлечь нацело есть бесконечная десятичная непериодическая дробь есть число иррациональное.

Рассмотрим приближенное значение с недостатком и с избытком:

С недостатком: 1,4; 1,41; 1,414; 1,4142

С избытком: 1,5; 1,42; 1,415; 1,4143

Объединим эти последовательности: 1,4 данную последовательность определяют два числа, не равные между собой, а это невозможно => последовательности определяют единственное число . Действия над иррациональными числами:1) сравнение (можно как десятичные дроби, сравнивая кол-во единиц в соответствующих разрядах, можно как квадраты корней);2) сложение, вычитание, умножение, деление (нельзя выполнять как с десятичными дробями).

2.14Методика изучения процентов. Основные задачи на проценты в школьном курсе математики.

При изучение этого материала нужно сначала уч-мся объяснить, что такое сотая часть числа (напр, сотая часть метра – это см, сотая часть центнера – кг) надо отметить, что к этому времени уч-ся уже прошли деление и дроби, и у них не возникнет проблем. Люди давно заметили, что сотые доли величин удобны в практич д-ти (напр, при записи десятич дробей). Потому для них было придумано спец название – процент. Значит, а один см – один процент от 1м. Итак, 1 процент – это 1 сотая доля. Здесь важно обратить внимание на мат запись процентов " % ", и главное объяснить, что целая часть равна 100%. Также надо обратить внимание на свойства.

Найти В процентов.

Пример найти 7% от числа 17.

7% от 17 будет 7*17/100 = 1.19 или одна целая девятнадцать сотых это семь процентов от семнадцати.

Также нужно отметить, что проценты это аналог обыкнов дробям ( 1/100 ) из этого следует, что процентами выполняются все 4 действия присущие обыкнов дробям. Так что при изучение темы проценты можно опираться на уже изученную тему по обыкновенным дробям.

Чтобы найти процентное отношение двух чисел А и В, надо отношение этих чисел умножить на 100%, то есть вычислить (а/в)*100%.

Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.

Одним из основных понятий математики является понятие числа. Изучение математики открывает знакомство с простейшим видом чисел — натуральными, и все последующее ее изучение связано с понятиями различных видов чисел.

Непосредственно связанным с понятием числа является понятие величины. Пожалуй, первые представления о величинах, а именно о частном виде величин — количестве предметов во множестве, было освоено людьми даже раньше, чем представление о числах. А дальнейшее историческое развитие понятия числа связано с развитием понятия величины и обусловлено им. По мере расширения понятия величины, введения новых видов величин, вводились, создавались, изобретались и новые классы чисел.

Математика изучает отдельные виды величин и чисел, дает им определения и устанавливает правила действий с числами и приёмы измерения величин. Но она не дает общего определения числа или величины вообще. Поэтому в школе изучается, главным образом, аппарат действий над разными видами чисел и измерения основных видов величин.

3.1. Различные подходы к введению числовых множеств

Исторически числовые множества расширялись следующим образом: N → N +→ а/в - → Z - → Q → R ., в современной математике порядок изучения чисел другой: : NcZcQcRcC .

В основе построения нового числового множества лежит принцип расширения, формулируемый следующим образом: «Пусть множество А расширяется до множества В, тогда необходимо выполнение следующих условий:

1. А В.

2. Все операции и отношения, выполняемые в А , должны выполнятся в В.

3. В В выполняется та операция, которая не выполняется в А.

4. Расширение идет по минимальности. (Нельзя N сразу расширить до Q).

В школьном курсе число будет считаться введенным, если:

– дано определение этого числа (часто описательного характера),

вытекающее из мотивирования необходимости его введения;

– для введенных чисел определяются отношения: =, >, , с*в = а).

Лучшему усвоению учащимися множества натуральных чисел способствует изучение некоторых вопросов делимости. По отношению делимости на данное натуральное число n множество N разбивается на два непересекающихся класса: натуральные числа, делящиеся на n и натуральные числа, не делящиеся на n. По числу делителей - , , . Рассматриваются признаки делимости на 2, 3, 5, 9, 10 и деление с остатком.

В результате изучения натуральных чисел у учащихся на наглядно-интуитивной основе должно быть сформировано:

1. знание свойств натуральных чисел (множество N - бесконечно, дискретно, упорядоченно, ограничено снизу);

2. понимание того факта, что операция умножения на N не определяется;

3. определение операции вычитание, умножение и деление;

4. умение работать с числами 0 и 1.

Теоретический материал в учебниках излагается в виде фрагментов, а затем идет решение задач и примеров.

В учебнике 5-го класса приводятся определения следующих понятий:

- натуральное число, десятичная запись числа, миллиард,

- сумма, разность, произведение двух натуральных чисел,

- делитель числа, кратные числа,

- совершенное число, простое число, дружественные числа.

3.3.Методика изучения дробных чисел

Основным источником получения дробных чисел является практическая деятельность (дробь, как результат измерения, результат деления целого на равные части, как частное от деления целого числа на другое натуральное число). В учебнике Н.Я. Виленкина приводятся все три способа получения дробных чисел.

Первое знакомство учащихся с обыкновенными дробями происходит в 3 классе параллельно с изучением натуральных чисел. В 5 классе начинается систематическое изучение дробей. Десятичные дроби для учащихся не являются новыми числами по сравнению с обыкновенными дробями. Они представляют лишь другую запись ранее известных обыкновенных дробей со знаменателями 10, 100, 1000, так как в математических расчетах и при проведении практических работ наиболее удобны десятичные числа.

В методике математики существует проблема порядка изучения десятичных и обыкновенных дробей.

Возможные подходы к ее решению:

- сначала изучаются десятичные дроби, а потом – обыкновенные;

- сначала изучаются обыкновенные дроби;

- смешанный вариант изучения дробей.

В существующих учебниках придерживаются третьего варианта.

Порядок изучения дробей

5 класс	6 класс
Обыкновенные дроби	Обыкновенные дроби
Сравнение, сложение и вычитание дробей с одинаковыми знаменателями	Сравнение дробей
Десятичные дроби	Арифметические действия с дробями
Четыре действия с десятичными дробями	Процент (по сути, изучение дес. дробей)

Важным элементом методики изучения дробных чисел является убеждение учащихся в целесообразности их введения.

Вторым приемом является тот факт, что с их помощью операция деления натуральных чисел делается всегда выполнимой.

Третий прием связан с измерением величин.

3.3.1. Обыкновенные дроби

Методика введения обыкновенных дробей

В 5 классе происходит лишь знакомство учащихся с обыкновенными дробями, их изучение продолжается в 6 классе.

Читайте также: