Метод наискорейшего спуска кратко
Обновлено: 05.07.2024
Основным недостатком градиентного метода является необходимость частого вычисления производных от функции F(х). Этого недостатка лишен метод наискорейшего спуска, который заключается в следующем.
В текущей точке вычисляется Grad F(X), и затем в направлении градиента ищется Min F(X). Практически это может быть осуществлено любым методом одномерной оптимизации (поиск по одному направлению – направление градиента), наиболее часто используется сканирование до первого локального минимума по направлению Grad F(X).
В результате вдали от оптимума эффективность метода повышается, мы быстрее попадем в район оптимума, в окрестности которого эффективность метода снижается из-за частой смены направления поиска и приближается к эффективности метода градиента.
В методе наискорейшего спуска в качестве направления поиска выбирается вектор, направление которого противоположно направлению вектора градиента функции ▽f(x). Из математического анализа известно, что вектор grad f(x)=▽f(x) характеризует направление наиболее быстрого возрастания функции (см. градиент функции). Поэтому вектор - grad f (X) = -▽f(X) называется антиградиентом и является направлением наиболее быстрого ее убывания. Рекуррентное соотношение, с помощью которого реализуется метод наискорейшего спуска, имеет вид Xk+1=Xk - λk▽f(xk), k = 0,1.
где λk>0 - величина шага. В зависимости от выбора величины шага можно получить различные варианты градиентного метода. Если в процессе оптимизации величина шага λ фиксирована, то метод носит название градиентного метода с дискретным шагом. Процесс оптимизации на первых итерациях можно значительно ускорить, если λk выбирать из условия λk=min f(Xk + λSk) .
Для определения λk используется любой метод одномерной оптимизации. В этом случае метод называется методом наискорейшего спуска. Как правило, в общем случае недостаточно одного шага для достижения минимума функции, процесс повторяют до тех пор, пока последующие вычисления позволяют улучшать результат.
Если пространство очень вытянуто по некоторым переменным, то образуется “овраг”. Поиск может замедлиться и идти зигзагами поперек дна “оврага”. Иногда решение невозможно получить за приемлемое время.
Еще одним недостатком метода может быть критерий остановки |▽f(Xk)| , так как этому условию удовлетворяет и седловая точка, а не только оптимум.
Пример 1 . Начиная из точки xk=(-2, 3) определите точку xk+1 методом наискорейшего спуска для минимизации функции f(x)=3x1 2 +x2 2 -x1x2-4x1 → min .
В качестве направления поиска выберем вектор градиент в текущей точке
Проверим критерий остановки |▽f(X1)| . Имеем |▽f(X1)|=20.1>0.1.
Вычислим значение функции в начальной точке f(X1) = 35. Сделаем
шаг вдоль направления антиградиента
Вычислим значение функции в новой точке
f(X2) = 3(-2 + 19λ1) 2 + (3-8λ1) 2 - (-2 + 19λ1)(3-8λ1) - 4(-2 + 19λ1)
Найдем такой шаг, чтобы целевая функция достигала минимума вдоль этого направления. Из необходимого условия существования экстремума функции
f’(X2) = 6(-2 + 19λ1) 19 + 2(3-8λ1)( -8) – (73 - 304 λ1) – 4*19
или f’(X2) = 2598 λ1 – 425 = 0.
Получим шаг λ1 = 0.164
Выполнение этого шага приведет в точку
в которой значение градиента |▽f(X2)|=2.02>0.1, значение функции f(X2) = 0.23. Точность не достигнута, из точки делаем шаг вдоль направления антиградиента ▽f(X2).
Пример №3 . Найти максимум функции f(x) методом Коши (методом наискорейшего спуска).
f(x) = 4x1 + 2x2 – x1 2 – x2 2 + 5 → max
x 0 =[4;5]
Безусловная оптимизация. Метод наискорейшего спуска
Информация о материале Обновлено: 11.05.2017, 19:53 Категория: Системы уравнений и задачи оптимизации


- это значения аргумента функции (управляемые параметры) на вещественной области.

В соответствии с рассматриваемым методом экстремум (максимум или минимум) целевой функции определяют в направлении наиболее быстрого возрастания (убывания) функции, т.е. в направлении градиента (антиградиента) функции. Градиентом функции в точке называется вектор, проекциями которого на координатные оси являются частные производные функции по координатам:

где i, j,…, n - единичные векторы, параллельные координатным осям.

Градиент в базовой точке строго ортогонален к поверхности, а его направление показывает направление наискорейшего возрастания функции, а противоположное направление (антиградиент), соответственно, показывает направление наискорейшего убывания функции.
Метод наискорейшего спуска является дальнейшим развитием метода градиентного спуска. В общем случае процесс нахождения экстремума функции является итерационной процедурой, которая записывается следующим образом:


- единичный вектор направления, который определяется по формуле:


- модуль градиента определяет скорость возрастания или убывания функции в направлении градиента или антиградиента:


- константа, определяющая размеры шага и одинаковая для всех i-х направлений.
Величина шага выбирается из условия минимума целевой функции f(х) в направлении движения, т. е. в результате решения задачи одномерной оптимизации в направлении градиента или антиградиента:


Другими словами, величину шага определяют при решении данного уравнения:

Таким образом, шаг расчета выбирается такой величины, что движение выполняется до тех пор, пока происходит улучшение функции, достигая, таким образом, экстремума в некоторой точке. В этой точке вновь определяют направление поиска (с помощью градиента) и ищут новую точку оптимума целевой функции и т.д. Таким образом, в данном методе поиск происходит более крупными шагами, и градиент функции вычисляется в меньшем числе точек.
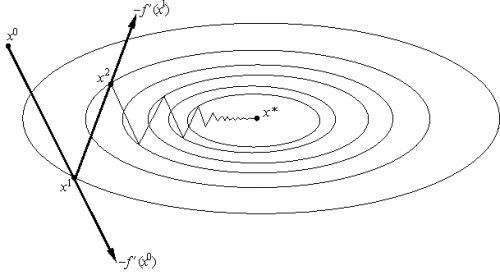
В случае функции двух переменных данный метод имеет следующую геометрическую интерпретацию: направление движения из точки касается линии уровня в точке . Траектория спуска зигзагообразная, причем соседние звенья зигзага ортогональны друг другу. Условие ортогональности векторов направлений спуска в соседних точках записывается следующим выражением:


Рис.1. Траектория движения к точке экстремума при использовании метода наискорейшего спуска, изображенная на графике линии равного уровня функции f(x)
Поиск оптимального решения завершается в случае, когда на итерационном шаге расчета (несколько критериев):
- траектория поиска остается в малой окрестности текущей точки поиска:

- приращение целевой функции не меняется:

- градиент целевой функции в точке локального минимума обращается в нуль:

Следует отметить, что метод градиентного спуска оказывается очень медленным при движении по оврагу, причём при увеличении числа переменных целевой функции такое поведение метода становится типичным. Овраг представляет собой впадину, линии уровня которой приближенно имеют форму эллипсов с различающимися во много раз полуосями. При наличии оврага траектория спуска имеет вид зигзагообразной линии с малым шагом, вследствие чего результирующая скорость спуска к минимуму сильно замедляется. Это объясняется тем, что направление антиградиента этих функций существенно отклоняется от направления в точку минимума, что приводит к дополнительной задержке в расчете. В результате алгоритм теряет вычислительную эффективность.

Метод градиента вместе с его многочисленными модификациями является распространенным и эффективным методом поиска оптимума исследуемых объектов. Недостатком градиентного поиска (так же и рассмотренных выше методов) является то, что при его использовании можно обнаружить только локальный экстремум функции. Для отыскания других локальных экстремумов необходимо производить поиск из других начальных точек. Так же скорость сходимости градиентных методов существенно зависит также от точности вычислений градиента. Потеря точности, а это обычно происходит в окрестности точек минимума или в овражной ситуации, может вообще нарушить сходимость процесса градиентного спуска.
Методика расчета

• 1 шаг: Определение аналитические выражения (в символьном виде) для вычисления градиента функции


• 2 шаг: Задаем начальное приближение
Далее выполняется итерационный процесс.
• 3 шаг: Определяется необходимость рестарта алгоритмической процедуры для обнуления последнего направления поиска. В результате рестарта поиск осуществляется заново в направлении скорейшего спуска.

• 4 шаг: Вычисление координат единичного вектора по представленным формулам



• 5 шаг: определяем шаг расчета из условия поиска экстремума для следующей функции (решения задачи одномерной оптимизации).

• 6 шаг: Определяем новые значения аргументов функции после выполнения k-го шага расчета:

• 7 шаг: проверяем критерии останова итерационного процесса. Вычислительный процесс заканчивается, когда будет достигнута точка, в которой оценка градиента будет равна нулю (коэффициенты функции отклика становятся незначимыми). В противном случае возвращаемся к шагу 3 и продолжаем итерационный расчет.
Для того, чтобы добавить Ваш комментарий к статье, пожалуйста, зарегистрируйтесь на сайте.

но она используется лишь для визуализации метода градиентного спуска. В действительности функции могут быть гораздо сложнее и зависеть от произвольного числа аргументов, для которых решать системы уравнений достаточно хлопотное занятие. Или же, функция постоянно меняется и нам необходимо под нее подстраиваться для определения текущего положения точки минимума. Все эти задачи удобнее решать с позиции алгоритмов направленного поиска, например, градиентного спуска.
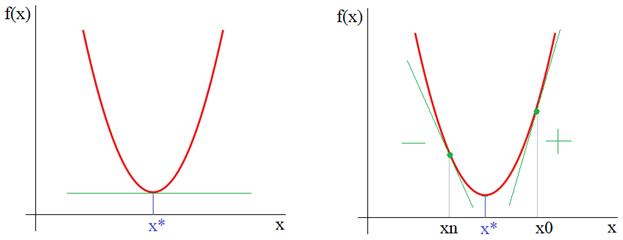
Итак, из рисунка мы хорошо видим, что справа от точки экстремума x* производная положительна, а слева – отрицательна. И это общее математическое правило для точек локального минимума. Предположим, что мы выбираем произвольную начальную точку на оси абсцисс. Теперь, смотрите, чтобы из двигаться в сторону x*, нам нужно в области положительных производных ее уменьшать, а в области отрицательных – увеличивать. Математически это можно записать так:

Здесь n – номер итерации работы алгоритма. Но, вы можете спросить: а где же тут градиент? В действительности, мы его уже учли чисто интуитивно, когда определяли перемещение вдоль оси абсцисс для поиска оптимальной точки x*. Но математика не терпит такой вульгарности, в ней все должно быть прописано и точно определено. Как раз для этого нужно брать не просто производную, а еще и определять направление движения, используя единичные векторы декартовой системы координат:


И градиент функции можно записать как

то есть, это будет уже направление вдоль оси ординат и направлен в сторону наибольшего увеличения функции. Соответственно, двигаясь в противоположную сторону, будем перемещаться к точке минимума x*.
Конечно, в результирующей формуле алгоритма поиска этот единичный вектор не пишется, а вместо него указывается разность по оси ординат, т.к. именно вдоль нее он и направлен:


которое, в общем случае, также может меняться от итерации к итерации. Этот множитель получил название шаг сходимости.
Давайте, для примера, реализуем этот алгоритм на Python для случая одномерной параболы. Вначале подключим необходимые библиотеки и определим две функции: параболу

и ее производную:

Затем, определим необходимые параметры алгоритма и сформируем массивы значений по осям абсцисс и ординат:
Далее, переходим в интерактивный режим работы с графиком, чтобы создать анимацию для перемещения точки поиска минимума и создаем окно с осями графика:
Отображаем начальный график:
Запускаем алгоритм градиентного поиска:
В конце выводим найденное значение аргумента и оставляем график на экране устройства:
После запуска увидим скатывание точки к экстремуму функции. Установим значение
Выбор шага сходимости

который обеспечивает и скорость и точность подбора аргумента x. В целом, это элемент творчества и, например, можно встретить и такой вариант изменения шага сходимости:

Функция min здесь выбирает наименьшее из двух аргументов и использует его в знаменателе дроби. Это необходимо, чтобы величина шага при больших n не становилась слишком маленькой и ограничивалась величиной

где mn – некоторое заданное ограничивающее значение.
Еще один прием связан с нормализацией градиента на каждом шаге работы алгоритма. В этом случае градиент функции (то есть, вектор):

приводится к единичной норме:

И уже он используется в алгоритме наискорейшего спуска:

В одномерном случае нашего примера, это, фактически означает, что вместо действительного значения градиента, берутся числа ±1:

И алгоритм в Python примет вид:
Как видите, такой подход требует уменьшения величины шага сходимости, на последующих итерациях, например, так:

Результат выглядит уже лучше и при этом, мы не привязаны к значению градиента.
Локальный минимум
Еще одной особенностью работы этого алгоритма является попадание в область локального минимума функции. Например, если взять вот такой график:


То при начальном значении x=0 получим один минимум, а, например, при x=2,5 – другой. В этом легко убедиться, если в нашей программе переписать функции:

(последняя – это производная: ). Увеличим диапазон отображения графика:
и запустим программу. Теперь, установим начальное значение xx=2,5, снова запустим и увидим уже другую точку локального минимума.
Это, наверное, основной недостаток данного алгоритма – попадание в локальный минимум. Чтобы решить эту проблему перебирают несколько разных начальных значений и смотрят: при котором был достигнуто наименьшее значение. Его и отбирают в качестве результата. Такой ход не дает нам гарантии, что действительно был найден глобальный минимум функции (иногда он может не существовать, как, например, с нашей синусоидой), но, тем не менее, это повышает наш шанс найти лучшее решение. Вот базовая теория и практика применения метода наискорейшего спуска.
Видео по теме










© 2022 Частичное или полное копирование информации с данного сайта для распространения на других ресурсах, в том числе и бумажных, строго запрещено. Все тексты и изображения являются собственностью сайта
В работе рассматривается задача поиска минимума функции , записываемая в виде:
Пусть функция такова, что можно вычислить ее градиент. Тогда можно применить метод градиентного спуска, описанный в данной статье.
В статье приведены теоремы сходимости метода градиентного спуска, а также рассмотрена его варианты:
- Метод градиентного спуска с постоянным шагом
- Метод градиентного спуска с дроблением шага
- Метод наискорейшего спуска
Метод градиентного спуска

Рис.1 Геометрическая интерпретация метода градиентного спуска с постоянным шагом. На каждом шаге мы сдвигаемся по вектору антиградиента, "уменьшенному в раз".
Идея метода
Основная идея метода заключается в том, чтобы осуществлять оптимизацию в направлении наискорейшего спуска, а это направление задаётся антиградиентом :
- постоянной, в этом случае метод может расходиться;
- дробным шагом, т.е. длина шага в процессе спуска делится на некое число;
- наискорейшим спуском:
Алгоритм
Выход: найденная точка оптимума
- Повторять:
- , где выбирается одним из описанных выше способов
- если выполен критерий останова, то возвращаем текущее значение
Критерий останова
Критерии остановки процесса приближенного нахождения минимума могут быть основаны на различных соображениях. Некоторые из них:
Здеcь - значение, полученное после -го шага оптимизации. - наперед заданное положительное число.
Сходимость градиентного спуска с постоянным шагом
Теорема 1 о сходимости метода градиентного спуска спуска с постоянным шагом.
Пусть , функция дифференцируема, ограничена снизу. Пусть выполняется условие Липшица для градиента : . Пусть .
Тогда при любом выборе начального приближения.
В условиях теоремы градиентный метод обеспечивает сходимость либо к точной нижней грани (если функция не имеет минимума) либо к значению Существуют примеры, когда в точке реализуется седло, а не минимум. Тем не менее, на практике методы градиентного спуска обычно обходят седловые точки и находят локальные минимумы целевой функции.
Определение. Дифференцируемая функция называется сильно выпуклой (с константой ), если для любых и из справедливо
Теорема 2 о сходимости метода градиентного спуска спуска с постоянным шагом.
Пусть функция дифференцируема, сильно выпукла с константой . Пусть выполняется условие Липшица для градиента : . Пусть .
Тогда при любом выборе начального приближения.
Выбор оптимального шага

Константа , фигурирующая в теореме 2 и характеризующая скорость сходимости метода, зависит от шага . Нетрудно видеть, что величина минимальна, если шаг выбирается из условия , т. е. если .
При таком выборе шага оценка сходимости будет наилучшей и будет характеризоваться величиной:
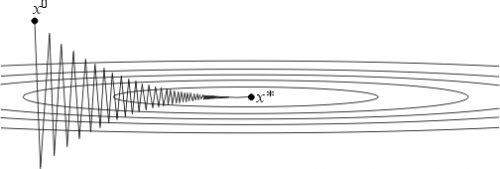
В качестве и могут выступать равномерные по x оценки сверху и снизу собственных значений оператора . Если , то и метод сходится очень медленно. Геометрически случай соответствует функциям с сильно вытянутыми линиями уровня (см. рис. 2). Простейшим примером такой функции может служить функция на , задаваемая формулой:
Поведение итераций градиентного метода для этой функции изображено на рис. 2 — они, быстро спустившись на "дно оврага", затем медленно "зигзагообразно" приближаются к точке минимума. Число (характеризующее, грубо говоря, разброс собственных значений оператора ) называют числом обусловленности функции . Если , то функции называют плохо обусловленными или овражными. Для таких функций градиентный метод сходится медленно.
Но даже для хорошо обусловленных функций проблема выбора шага нетривиальна в силу отсутствия априорной информации о минимизируемой функции. Если шаг выбирается малым (чтобы гарантировать сходимость), то метод сходится медленно. Увеличение же шага (с целью ускорения сходимости) может привести к расходимости метода. Далее будут описаны два алгоритма автоматического выбора шага, позволяющие частично обойти указанные трудности.
Градиентный метод с дроблением шага
В этом варианте градиентного метода величина шага на каждой итерации выбирается из условия выполнения неравенства
где - некоторая заранее выбранная константа.
Процедуру нахождения такого обычно оформляют так. Выбирается число и некоторый начальный шаг . Теперь для каждого k полагают и делают шаг градиентного метода. Если с таким условие (2) выполняется, то переходят к следующему k. Если же (2) не выполняется, то умножают на ("дробят шаг") и повторяют эту процедуру до тех пор пока неравенство (2) не будет выполняться. В условиях теоремы 1 эта процедура для каждого k за конечное число шагов приводит к нужному .
Можно показать, что в условиях теоремы 2 градиентный метод с дроблением шага линейно сходится. Описанный алгоритм избавляет нас от проблемы выбора на каждом шаге, заменяя ее на проблему выбора параметров и , к которым градиентный метод менее чувствителен. При этом, разумеется, объем вычислений возрастает (в связи с необходимостью процедуры дробления шага), впрочем, не очень сильно, поскольку в большинстве задач основные вычислительные затраты ложатся на вычисление градиента.
Метод наискорейшего спуска

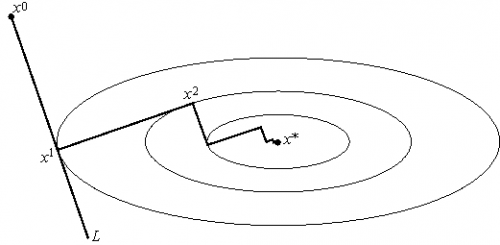
Рис.3 Геометрическая интерпретация метода наискорейшего спуска. На каждом шаге выбирается так, чтобы следующая итерация была точкой минимума функции на луче L.
Этот вариант градиентного метода основывается на выборе шага из следующего соображения. Из точки будем двигаться в направлении антиградиента до тех пор пока не достигнем минимума функции f на этом направлении, т. е. на луче :
Другими словами, выбирается так, чтобы следующая итерация была точкой минимума функции f на луче L (см. рис. 3). Такой вариант градиентного метода называется методом наискорейшего спуска. Заметим, кстати, что в этом методе направления соседних шагов ортогональны.
Метод наискорейшего спуска требует решения на каждом шаге задачи одномерной оптимизации. Практика показывает, что этот метод часто требует меньшего числа операций, чем градиентный метод с постоянным шагом.
В общей ситуации, тем не менее, теоретическая скорость сходимости метода наискорейшего спуска не выше скорости сходимости градиентного метода с постоянным (оптимальным) шагом.
Числовые примеры
Метод градиентного спуска с постоянным шагом
Для исследования сходимости метода градиентного спуска с постоянным шагом была выбрана функция:
Начальное приближение - точка (10,10). Использован критерий останова:
Результаты эксперимента отражены в таблице:
| Значение шага | Достигнутая точность | Количество итераций |
|---|---|---|
| 0.1 | метод расходится | |
| 0.01 | 2e-4 | 320 |
| 0.001 | 2e-3 | 2648 |
| 0.0001 | 1e-2 | 20734 |
Из полученных результатов можно сделать вывод, что при слишком большом чаге метод расходится, при слишком малом сходится медленно и точчность хуже. Надо выбирать шаг наибольшим из тех, при которых метод сходится.
Градиентный метод с дроблением шага
Для исследования сходимости метода градиентного спуска с дроблением шага (2) была выбрана функция:
Начальное приближение - точка (10,10). Использован критерий останова:
Результаты эксперимента отражены в таблице:
| Значение параметра | Значение параметра | Значение параметра | Достигнутая точность | Количество итераций |
|---|---|---|---|---|
| 0.95 | 0.95 | 1 | 5e-4 | 629 |
| 0.1 | 0.95 | 1 | 1e-5 | 41 |
| 0.1 | 0.1 | 1 | 2e-4 | 320 |
| 0.1 | 0.95 | 0.01 | 2e-4 | 320 |
Из полученных результатов можно сделать вывод об оптимальном выборе параметров: , хотя метод не сильно чувствителен к выбору параметров.
Метод наискорейшего спуска
Для исследования сходимости метода наискорейшего спуска была выбрана функция:
Начальное приближение - точка (10,10). Использован критерий останова:
Для решения одномерных задач оптимизации использован метод золотого сечения.
Метод получил точность 6e-8 за 9 итераций.
Отсюда можно сделать вывод, что метод наискорейшего спуска сходится быстрее, чем градиентный метод с дроблением шага и метод градиентного спуска с постоянным шагом.
Недостатком методом наискорейшего спуска явлляется необходимость решать одномерную задачу оптимизации.
Рекомендации программисту
При программировании методов градиентного спуска следует аккуратно относится к выбору параметров, а именно
- Метод градиентного спуска с постоянным шагом: шаг следует выбирать меньше 0.01, иначе метод расходится (метод может расходится и при таком шаге в зависимости от исследуемой функции).
- Градиентный метод с дроблением шага не очень чувствителен к выбору параметров. Один из вариантов выбора параметров:
- Метод наискорейшего спуска: в качестве метода одномерной оптимизации можно использовать метод золотого сечения (когда он применим).
Заключение
Методы градиентного спуска являются достаточно мощным инструментом решения задач оптимизации. Главным недостатком методов является ограниченная область применимости.
Читайте также: