Линейная регрессия машинное обучение кратко

Обновлено: 02.07.2024

В этой статье мы расскажем о линейной регрессии — основополагающем алгоритме, с изучения которого начинается любой курс машинного обучения и науки о данных. Лучше всего, конечно, осваивать теорию на реальных проектах, а здесь мы постараемся рассказать о том, что же такое линейная регрессия и в чём её исключительная ценность

Линейная регрессия: кавер-версия бессмертного хита
Подготовка к погружению: проверка снаряжения
Что это?
Как это работает?
Линейная регрессия методом обыкновенных наименьших квадратов: начинаем погружение
Линейная регрессия методом градиентного спуска
Градиентный спуск, погружение: уровень 1
Цель обучения алгоритма машинного обучения – минимизировать функцию потерь
Градиентный спуск, погружение: уровень 2

Кто повторяет старое и узнаёт новое, тот может быть предводителем.

В этой статье мы расскажем о линейной регрессии — основополагающем алгоритме, с изучения которого начинается любой курс машинного обучения и науки о данных. Нелегко писать о столь популярном методе, не переходя сразу же на язык формул. К тому же, как ни странно, большее количество доступной информации не всегда способствует лучшему пониманию. Эффективнее всего, конечно, осваивать теорию на реальных проектах, а здесь мы постараемся как можно подробнее рассказать о том, что же такое линейная регрессия и в чём её исключительная ценность. Материал построен таким образом, чтобы вы сами решили, насколько глубоко хотите погрузиться в тему. Однако этой статьи не будет достаточно, чтобы вы смогли реализовать алгоритм с нуля, её главная цель – ваше интуитивное понимание и, конечно, ваш интерес к проблематике ИИ.

Прежде всего необходимо понимать, что линейная регрессия была разработана еще в XIX веке в области статистики для понимания взаимосвязи между данными ввода и вывода. Объяснимость – это одна из главных ценностей, можно сказать, Священный Грааль машинного обучения, к которому так стремятся исследователи ИИ (тот самый explainable AI). Именно объяснимость позволяет сделать наиболее точный прогноз, чем в первую очередь и занимается область прогнозного моделирования (predictive modeling), этой цели и служит вездесущая минимизация ошибки модели. Где только не применяется прогнозное моделирование данных: в сфере бизнеса и финансов, конечно, маркетинге и продажах, удержании клиентов, алгоритмической торговле; в науке – практически во всех сферах. Лишь бы было достаточное количество численных данных, а в них сейчас недостатка нет. Поэтому линейная регрессия была заимствована из статистики и получила такое широкое распространение в сферах машинного обучения и прогнозного моделирования: быстро, понятно, эффективно, открывает простор для творчества.

Кстати, знаете ли вы разницу между машинным обучением и прогнозным моделированием? Напишите, пожалуйста, в комментариях! Ответ будет в следующей статье цикла. А сейчас предлагаем вам погрузиться глубже в тему линейной регрессии (ассоциации с дайвингом настойчиво преследуют автора этой статьи по неизвестной причине).

Прежде всего давайте убедимся, что вы знакомы с понятиями, без которых дальше не обойтись.

В контексте машинного обучения линейная регрессия относится к разделу обучения с учителем (supervised learning), то есть когда явно прослеживается связь между вводом и выводом и предсказывается некое значение по ограниченному количеству примеров (на которых, как ученик, обучается алгоритм). Напомним, что обучение с учителем, или контролируемое обучение, делится на две категории: регрессия и классификация (о ней в следующих материалах).

Для обучения с учителем данные мы делим на обучающий (training set) и тестовый наборы (testing set): 80/20 – обычное соотношение. Обучающий набор — это данные, на которых алгоритмбудет учиться. Например, при использовании линейной регрессии точки в обучающем наборе используются для построения линии наилучшего соответствия (line of best fit). Тестовый набор будет использован для оценки качества модели.

На основе обучающих данных мы можем построить график (например, количество часов занятий студента на нем будет обозначено x, а его итоговый балл y) и определить функцию, которая будет очень похожа на этот график. Такую функцию называют функцией гипотезы (hypothesis function), в нашем случае это будет одномерная линейная регрессия (с одной переменной). Теперь на основе функции гипотезы можно сделать прогноз.

Точность функции гипотезы может быть измерена с помощью функции стоимости, или функции потерь. Почему она так называется? Потому что она характеризует потери при неправильном принятии решений на основе наблюдаемых данных. Функция потерь принимает разницу между функцией гипотезы при значениях x и обучающей выборкой при тех же значениях x. Мы стремимся найти параметры функции потерь таким образом, чтобы ее выходные данные были минимальны.

Обучение модели – это и есть минимизация функции потерь, а для этого нужно двигаться в отрицательном направлении производной. Так мы сможем найти такую функцию гипотезы, которая точнее описывает наши обучающие данные. Предположим, что это будет одномерная (простая) линейная регрессия.

Линейная регрессия – это модель линейной зависимости одной (зависимой) переменной от другой или нескольких.

Математическое представление линейной регрессии достаточно легко для восприятия. Линия простой линейной регрессии задается уравнением вида y = β₀ + β₁x, где x – независимая переменная, y – зависимая. Как мы учили в 7 классе!

Простая линейная регрессия с одной независимой переменной (x): красные точки — это реальные значения, линия регрессии (y) — линия наилучшего соответствия, проходящая через точки графика разброса

Наклон линии на этом графике равен коэффициенту β₁, точка пересечения (перехват, intercept) определена в коэффициенте β₀ (то есть чему равен y при x = 0)_, этот коэффициент даёт нашей линии свободу передвижения вверх и вниз по двумерному пространству. Алгоритм при обучении стремится найти эти коэффициенты и таким образом определить регрессионную функцию (модель).

Когда на вводе одна переменная (x), это простая линейная регрессия, если их несколько – это уже множественная линейная регрессия. График линейной регрессии в двух измерениях (с единственной независимой переменной) — прямая линия, в трёх — плоскость, в четырёх и более — гиперплоскость.

За этой внешней простотой – огромный потенциал: мы увидим, как на основе этого метода с более чем двухсотлетней историей появилось множество невероятных идей и возможностей. Именно линейная регрессия лежит в основе многих новейших алгоритмов, находящихся на самом острие науки, включая глубокие нейронные сети.

Как уже упоминалось, цель алгоритма линейной регрессии – установить такие коэффициенты, чтобы стало возможно определить данную регрессионную модель, а достигается это в процессе обучения. Для этого существует целый ряд методов, однако наиболее популярные из них — это метод обыкновенных наименьших квадратов и краеугольный камень машинного обучения – градиентный спуск.

Для простоты приведём пример с одной независимой переменной. Предположим, что у нас есть некий набор точек наблюдения. Это может быть площадь квартир, рост людей и т. д., то есть любой фактор (регрессор), влияние которого вы хотите узнать (например, посмотреть зависимость роста и веса, площади жилья и его стоимости и т. д.). Конечно, в реальности чаще принимается во внимание не один фактор, а несколько, но на этот случай у нас есть множественная линейная регрессия.

Данные есть, а теперь вопрос: как прочертить прямую линию, которая была бы максимально приближена к этим точкам наблюдения?

e = y — ŷ (Реальное значение — Прогнозированное значение).

Геометрически это сумма длин отрезков между красными крестиками на графике (реальными значениями) и линией регрессии, которую еще называют линией тренда.

Значения ŷ лежат на линии регрессии, а красные крестики обозначают y. e = y — ŷ (Реальное значение — Прогнозированное значение)

Сумма отклонений возводится в квадрат (SSE — sum of squared errors) и минимизируется с помощью дифференциальных и матричных вычислений, которые мы, пожалуй, приводить не будем. Иногда минимизируется не сумма квадратичных отклонений, а среднеквадратичное значение отклонений (MSE — mean of squared errors).

Почему именно квадрат? Я всегда считала, что это делается для избавления от отрицательных значений, однако оказывается, что квадрат длин даёт гладкую функцию (которая имеет непрерывную производную), в то время как просто длина даёт функцию в виде конуса, недифференцируемую в точке минимума. (На тот случай, если любознательность тоже заводит вас далеко).

Метод наименьших квадратов, помимо очевидных достоинств, имеет и существенный недостаток – он плохо справляется с большим количеством данных на вводе (факторов, или попросту x_i). Если вы работаете с большими данными, ваш выбор – это градиентный спуск. Используя этот метод, вы занимаетесь машинным обучением в его классическом виде, потому что именно так обучаются нейросети, включая и сверхсовременные алгоритмы глубокого обучения, которые сейчас на самом острие науки.

Представьте себе, что вы стоите на вершине оврага и хотите спуститься вниз, но не знаете как. Вы будете шагать шире, когда склон более пологий, и мельче, когда склон более крутой. Ваш следующий шаг будет зависеть от предыдущего, а достигнув дна оврага, вы остановитесь. Этот образ поможет вам понять дальнейшие объяснения. Крутизну, или уклон, вашего оврага (крутизну в её первоначальном смысле, конечно!) и будет задавать градиент. Градиент, или уклон (slope), — это не что иное, как отношение изменений по оси y к изменениям по оси x.

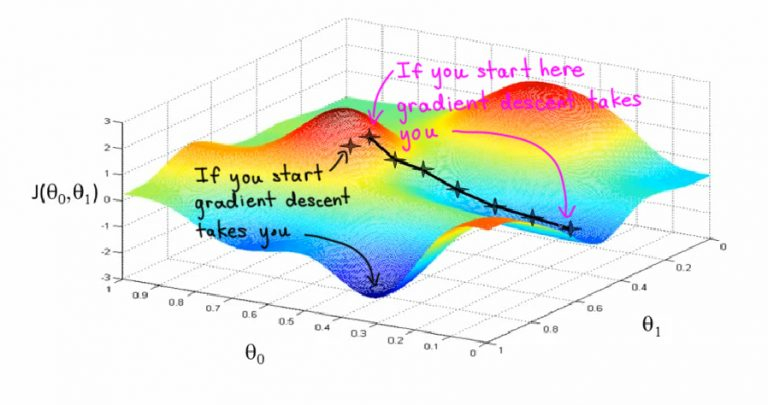
Градиентный спуск – это основной метод обучения нейронных сетей, с его помощью постепенно уточняются параметры нейронной сети (веса и смещение), чтобы таким образом минимизировать функцию потерь сети (cost function, loss function)

Цель обучения алгоритма машинного обучения – минимизировать функцию потерь

(Напоминаем, функция потери — разница между значениями меток обучения и прогноза, сделанного с помощью модели). Как это происходит?

Если говорить о простой линейной регрессии ( y = β₀ + β₁ x) в терминах машинного обучения, смещение (intercept) соответствует параметру β₀, а вес (weight) – параметру β₁. Сначала инициируются случайные значения для каждого коэффициента. Сумма квадратов ошибок вычисляется для каждой пары входных и выходных значений. Градиент ошибки будет подсчитываться с использованием частных производных функции потерь по весам и смещению.

Нам понадобится ещё коэффициент скорости обучения (learning rate), он также задается эмпирически. Этот параметр (обычно обозначается £), определяет размер шага по градиенту, выполняемого на каждой итерации, и отвечает за то, как будут корректироваться веса с учётом функции потерь. Чем меньше значение скорости обучения, тем медленнее движение по градиенту. При малом коэффициенте скорости обучения мы, скорее всего, не пропустим ни одной впадины (локального минимума), хотя рискуем застрять на плато, и тогда сходимости придётся подождать.

Процесс повторяется до тех пор, пока не будет достигнута минимальная сумма квадратов ошибок или пока не станет невозможным дальнейшее улучшение.

Градиентный спуск — это итеративный метод нахождения локального минимума функции с помощью движения вдоль градиента.

Давайте используем градиентный спуск для обучения простой линейной регрессии. Функцией гипотезы тогда будет линейная функция

Необходимо определить параметры нашей функции гипотезы с помощью функции стоимости, заданной таким образом:

Мы делим на m наши примеры из обучающего набора, обратите внимание, что двойка в знаменателе — это математическая уловка, которую мы используем, чтобы потом компенсировать 2 при взятии производной функции. В скобках разность реальных значений и прогнозов, потом вся она суммируется и возводится в квадрат.

Теперь нужно минимизировать функцию относительно её параметров:

Для простой линейной регрессии эти параметры можно установить равными нулю, а в случае множественной надо будет задать им случайные величины. Подбор параметров осуществляется путем итерации по нашему обучающему набору. Мы будем обновлять параметры согласно такой формуле:

где α – скорость обучения, а – производная, или уклон, функции стоимости, что даёт нам при подстановке

С каждой итерацией параметры будут обновляться, а функция будет стремиться к минимуму.

Вышеописанный алгоритм в англоязычных источниках называется Batch Gradient Descent, поскольку на каждой итерации задействуется весь обучающий набор (batch). Однако существуют такие разновидности этого алгоритма, как стохастический градиентный спуск и мини-пакетный градиентный спуск. Возможно, у вас возникнет желание ознакомиться с ними.

Регрессия – группа Моделей (Model) Контролируемого обучения (Supervised Learning) , используемых для прогнозирования непрерывных значений, таких как цены на недвижимость с учетом их характеристик (размер, цена и т.д.).

Выделяют следующие типы регрессионного анализа:

Линейная регрессия (Linear Regression)
Полиномиальная регрессия (Polynomial Regression)
Регрессия опорных векторов (SVR)
Регрессия Дерева решений (Decision Tree)
Регрессия Случайного леса (Random Forest)

Линейная регрессия

Это одна из наиболее распространенных и доступных техник предсказания. Здесь мы прогнозируем Целевую переменную (Target Variable) Y на основе Предиктора (Predictor Variable) X. Между первой и второй должна существовать линейная связь, и поэтому метод получил такое название.

Рассмотрим прогнозирование заработной платы сотрудника в зависимости от его возраста. Допустим, что существует корреляция между возрастом сотрудника и заработной платой (чем больше возраст, тем больше заработная плата). Гипотеза линейной регрессии такова:

Итак, чтобы предсказать Y (зарплату) с учетом X (возраста), нам нужно знать значения a и b (коэффициенты модели):

Во время обучения регрессионной модели именно эти коэффициенты изучаются и подгоняются к обучающим данным. Цель тренировки – найти наиболее подходящую линию, минимизирующую Функцию потерь (Loss Function) . Последняя помогает измерить ошибку между фактическими и прогнозируемыми значениями.

На рисунке розовые точки – это реальные Наблюдения (Observation) – пары координат "Возраст – Зарплата", а белая линия – прогнозируемые значения оклада в зависимости от возраста. Чтобы сравнить реальное и прогнозируемое значения, точки фактических данных проецируются на линию.

Наша цель – найти такие значения коэффициентов, которые минимизируют функцию стоимости. Наиболее распространенная функция стоимости – это Среднеквадратичная ошибка (MSE) , которая равна среднему квадрату разницы между фактическими и прогнозируемыми значениями наблюдения:

Значения коэффициентов могут быть рассчитаны с использованием подхода Градиентного спуска (Gradient Descent). Чтобы дать Вам первое представление, в градиентном спуске мы начинаем с некоторых случайных значений коэффициентов, вычисляем градиент функции потерь по этим значениям, обновляем коэффициенты и снова вычисляем функцию стоимости. Этот процесс повторяется до тех пор, пока мы не найдем минимальное значение функции стоимости.

Полиномиальная регрессия

В полиномиальной регрессии мы преобразуем исходные Признаки (Feature) в полиномиальные заданной степени, а затем применяем к ним линейную регрессию. Рассмотрим преобразованную линейную модель Y = a + bX:

Это все еще линейная модель, но кривая теперь квадратичная, а не прямая:

Если мы увеличим степень до очень высокого значения, до достигнем Переобучения (Overfitting) , поскольку модель также "загребает" и Шум (Noise).

Регрессия опорных векторов

В SVR мы идентифицируем гиперплоскость с максимальным запасом, так что максимальное количество точек данных находится в пределах этого поля. SVR почти аналогична Методу опорных векторов (SVM) :

Вместо того, чтобы минимизировать частоту ошибок, как в простой линейной регрессии, мы пытаемся уместить ошибку в пределах определенного порога. Наша цель в SVR состоит в том, чтобы в основном учитывать моменты, которые находятся в пределах допуска. Наша лучшая линия – это гиперплоскость с максимальным количеством точек:

Регрессия дерева решений

Деревья решений могут использоваться как для Классификации (Classification) , так и для регрессии. В деревьях решений на каждом уровне нам нужно идентифицировать атрибут разделения.

Дерево решений строится путем разделения данных на подмножества, содержащие экземпляры с однородными значениями. Стандартное отклонение (Standard Deviation) используется для расчета однородности числовой Выборки (Sample) . Если числовая выборка полностью однородна, ее стандартное отклонение равно нулю.

Шаги по поиску узла расщепления кратко описаны ниже:

Рассчитайте стандартное отклонение целевой переменной
Разделите набор данных на разные атрибуты и вычислите стандартное отклонение для каждой ветви (стандартное отклонение для целевой переменной и предиктора). Это значение вычитается из стандартного отклонения перед разделением. Результатом является уменьшение стандартного отклонения.
В качестве узла разделения выбирается атрибут с наибольшим уменьшением стандартного отклонения.
Набор данных делится на основе значений выбранного атрибута. Этот процесс выполняется рекурсивно.

Чтобы избежать переобучения, используется коэффициент отклонения, который решает, когда прекратить ветвление. Наконец, среднее значение каждой ветви присваивается соответствующему конечному узлу (при регрессии берется среднее значение).

Регрессия Случайного леса

Случайный лес – это Ансамблевый (Ensemble) подход, в котором мы учитываем прогнозы нескольких деревьев регрессии:

Выберите K случайных точек
Определите n – количество создаваемых регрессоров дерева решений. Повторите шаги 1 и 2, чтобы создать несколько деревьев регрессии.
Среднее значение каждой ветви назначается конечному узлу в каждом дереве решений.
Чтобы предсказать результат для переменной, учитывается среднее значение всех прогнозов всех деревьев решений.

Случайный лес предотвращает переобучение (что является обычным для деревьев решений) путем создания случайных подмножеств признаков и построения меньших деревьев с использованием этих подмножеств.

Автор оригинальной статьи: Apoorva Dave

Сталкиваясь с какой-либо проблемой в ML, помните, что есть множество алгоритмов, позволяющих её решить. Однако не существует такого универсального алгоритма, который подходил бы под все случаи и решал абсолютно все проблемы.

Выбор алгоритма строго зависит от размера и структуры ваших данных. Таким образом, выбор правильного алгоритма может быть неясен до тех пор, пока мы не проверим возможные варианты и не наткнёмся на ошибки.

Но каждый алгоритм обладает как преимуществами, так и недостатками, которые можно использовать в качестве руководства для выбора наиболее подходящего под ситуацию.

Начнём с простого. Одномерная (простая) линейная регрессия – это метод, используемый для моделирования отношений между одной независимой входной переменной (переменной функции) и выходной зависимой переменной. Модель линейная.

Более общий случай – множественная линейная регрессия, где создаётся модель взаимосвязи между несколькими входными переменными и выходной зависимой переменной. Модель остаётся линейной, поскольку выходное значение представляет собой линейную комбинацию входных значений.

Также стоит упомянуть полиномиальную регрессию. Модель становится нелинейной комбинацией входных переменных, т. е. среди них могут быть экспоненциальные переменные: синус, косинус и т. п. Модели регрессии можно обучить с помощью метода стохастического градиента.

Преимущества:

Быстрое моделирование. В особенности, моделирование можно назвать простым, если отсутствует большой объём данных.
Линейную регрессию легко понять. Она может быть ценна для различных бизнес-решений.

Недостатки:

В случае нелинейных данных полиномиальную регрессию трудно спроектировать. Необходимо иметь информацию о структуре данных и взаимосвязи между переменными.
Основываясь на изложенных выше фактах, линейная регрессия неэффективна, когда речь идёт об очень сложных данных и больших объёмах.

Нейронные сети тренируются с помощью метода стохастического градиента и алгоритма обратного распространения ошибки.

Преимущества:

Так как нейронные сети могут быть многослойными, они эффективны при моделировании сложных нелинейных отношений.
Нам не нужно беспокоиться о структуре данных в нейронных сетях, которые очень гибки в изучении почти любого типа переменных признаков.
Исследования постоянно показывают: чем больше обучающих данных “дают” нейронной сети, тем производительнее она становится.

Недостатки:

Из-за сложности этой модели, её нелегко понять и реализовать.
Нейронные сети требуют тщательной настройки гиперпараметров и скорости обучения.
Для достижения высокой производительности нейронным сетям необходимо огромное количество данных, и в результате, как правило, нейросети уступают другим ML алгоритмам в тех случаях, когда данных мало.

Начнём с простого случая. Дерево принятия решений – это представления правил, находящихся в последовательной, иерархической структуре, где каждому объекту соответствует узел, дающий решение. При построении дерева важно классифицировать атрибуты так, чтобы создать “чистые” узлы. То есть выбранный атрибут должен разбить множество так, чтобы получаемые в итоге подмножества состояли из объектов, принадлежащих к одному классу, или были максимально приближены к этому, т.е. количество объектов из других классов в каждом из этих множеств было как можно меньше.

Линейная регрессия, пожалуй, один из самых известных и хорошо понятных алгоритмов в статистике и машинном обучении.

В этом уроке вы откроете для себя алгоритм линейной регрессии, как он работает и как вы можете наилучшим образом использовать его в своих проектах машинного обучения. В этом уроке вы узнаете:

Почему линейная регрессия относится как к статистике, так и к машинному обучению.

Другие псевдонимы, которыми называется линейную регрессией.
Алгоритмы представления и обучения, используемые для создания модели линейной регрессии.
Как подготовить данные при моделировании с помощью линейной регрессии.

Вам не нужно знать статистику или линейную алгебру, чтобы понять устройство линейной регрессии (хоть это безусловно и помогает). Это верхнеуровневое введение , чтобы дать вам достаточно технической базы и иметь возможность эффективно использовать алгоритм для своих собственных проблем и задач.

Разве линейная регрессия происходит не от статистики?

Прежде чем мы погрузимся в детали линейной регрессии, вы можете спросить себя, почему мы смотрим на этот алгоритм.

Разве это не техника из статистики?

Машинное обучение, в частности, область прогнозного моделирования в первую очередь связана с минимизацией ошибки модели или созданием наиболее точных прогнозов, за счет объяснимости. При применении машинного обучения мы будем заимствовать, повторно использовать и "воровать" алгоритмы из разных областей, включая статистику, и использовать их в этих целях.

Таким образом, линейная регрессия была разработана в области статистики и изучается в качестве модели для понимания взаимосвязи между входными и выходными числовыми переменными, но заимствована машинным обучением. Это одного и статистический алгоритм, и алгоритм машинного обучения.

Далее рассмотрим некоторые из общих имен, используемых для обозначения модели линейной регрессии.

Многоликость линейной регрессии

Когда вы начинаете смотреть алгоритм линейной регрессии, все может казаться очень запутанным.

Алгоритм существует более 200 лет уже был изучен со всех возможных точек зрения и часто каждый новых угол имеет предназначение и другое название.

Линейная регрессия — это линейная модель, которая предполагает линейную связь между входными переменными (Xi) и единственной переменной на вывода (Y). Более конкретно, что у может быть рассчитана через линейную комбинации входных переменных (X) (или У = B1*X1 + B2*X2 + ..Bn*Xn).

При наличии одной переменной ввода (x) метод называется простой линейной регрессией. Когда существует несколько переменных входных данных, литература из статистики часто называет метод множественной линейной регрессией.

Различные методы могут быть использованы для подготовки или обучения линейной регрессии. Наиболее распространенным из которых называется Метод наименьших квадратов (или сокращенно МНК, по-английски это Ordinary Least Squares или OLS).

Теперь, когда вы знаете некоторые названия, используемые для описания линейной регрессии, давайте подробнее рассмотрим используемое представление.

Представление модели линейной регрессии

Линейная регрессия является привлекательной моделью, потому что ее представление очень простое.

Представление - это линейное уравнение, объединяющее определенный набор входных значений (X) решений, к которому является прогнозируемый вывод для этого набора входных значений (y). Таким образом, как значения входных данных (x), так и выходное значение являются числовыми.

Линейное уравнение присваивает масштабный коэффициент (по-английски "scale factor") к каждому входному значению X. Масштабный коэффициент представлен греческой буквой Beta (B). Добавлен также один дополнительный коэффициент, добавляющую дополнительную степень свободы (например, движение вверх и вниз по двумерном участку) и часто называют коэффициентом перехвата или смещения (по-английски "bias coefficient").

Наиболее простая задача регрессии когда на вход подается одна переменная X и есть одно выходящее значение Y. Форма подобной модели будет:

В случае многомерных измерений (т.е. когда у нас есть более одной вводной переменной (X)), линия превращается в плоскостью или гипер-плоскости. Таким образом, представление представляет собой форму уравнения и конкретные значения, используемые для коэффициентов (например, B0 и B1 в приведенном выше примере).

Когда говорят о сложности регрессионной модели, такой как линейная регрессия - имеют ввиду количество коэффициентов, используемых в модели.

Когда конкретный элемент коэффициент Beta становится нулевым, он эффективно удаляет влияние входной переменной на модель и, следовательно, влияния на прогноз модели (0 * Xi = 0). Это становится актуальным, если вы применяете методы регуляризации (о них мы расскажем отдельно), которые изменяют алгоритм обучения, чтобы уменьшить сложность моделей регрессии, оказывая давление на абсолютный размер коэффициентов, приводя некоторые из них к нулю.

Теперь, когда мы понимаем что представление, используемое для модели линейной регрессии, давайте рассмотрим некоторые способы, с помощью которых мы можем узнать это представление из данных.

Методы линейной регрессии

Изучение модели линейной регрессии означает исследование получаемых значений коэффициентов, используемых в представлении, на основе имеющихся входных данных.

В этой части урока мы кратко рассмотрим четыре метода для подготовки модели для линейной регрессии. Это не достаточно информации для реализации их с нуля, но достаточно, чтобы получить первые впечатления и компромиссы при их вычислении.

Есть еще много методов, потому что модель линейной регрессии так хорошо изучены. Важно обратить внимание что на метод наименьших квадратов, потому что это наиболее распространенный метод, используемый в целом в индустрии для задач оптимизации. Также обратите внимание метод Градиентного спуска (по-английски Gradient descent), как наиболее распространенный метод применяемый в различных классах задач машинного обучения.

Простая линейная регрессия

При простой линейной регрессии, когда у нас есть один входной параметр, мы можем использовать статистику для оценки коэффициентов.

Для этого необходимо вычислить статистические свойства на таких данных, как среднее значение, стандартные отклонения, корреляции и ковариантность. Все данные должны быть доступны для обхода и расчета статистик.

Это весело, как упражнение полезно однажды проделать в Excel, но не очень полезно на практике.

Метод Наименьших Квадратов

Когда у нас есть более одной входной переменной, мы можем использовать метод наименьших квадратов для оценки значений коэффициентов.

Процедура наименьших квадратов направлена на минимизацию суммы квадратов остатков. Это означает, что, учитывая регрессионную линию через данные, мы вычисляем расстояние от каждой входной точки Xi до линии регрессии, берем квадрат этого расстояние и суммируем все квадраты подобных расстояний. Это количество, которое обычные наименее квадратов стремится свести к минимуму.

Такой подход рассматривает данные как матрицу и использует операции линейной алгебры для оценки оптимальных значений коэффициентов. Это означает, что все данные должны быть доступны, и вы должны иметь достаточно памяти, чтобы соответствовать размеру датасета и выполнять матричные операции.

Руками подобные вычисления уже давно никто не делает (кроме как для собственного понимания или в рамках домашнего задания в школе или ВУЗе). Вы просто вызываете процедуру из библиотеки линейной алгебры. Эта процедура умеет быстро вычислять подобные задачи.

Градиентный спуск

При наличии одной или нескольких переменных можно использовать процесс оптимизации значений коэффициентов путем итеративной минимизации ошибки модели на обучающихся данных.

Эта операция называется Градиентный спуск и работает, начиная со случайных значений для каждого коэффициента.

По аналогии с методов наименьших квадратов - мы ищем сумму ошибок в квадрате рассчитывается для каждой пары входных и выходных значений. В качестве масштабного коэффициента в градиентном спуске используется частота обучения (по-английски "learn rate"), а коэффициенты обновляются в направлении минимизации ошибки. Процесс повторяется до тех пор, пока не будет достигнута ошибка в квадрате минимальной суммы или не возможно дальнейшее улучшение.

При использовании этого метода необходимо выбрать параметр скорости обучения (альфа), который определяет размер шага улучшения, чтобы взять на себя каждую итерацию процедуры.

На практике градиентный спуск является полезным методом, когда у вас очень большой датасет либо в количестве строк, либо в количестве столбцов, которые могут не уместиться в памяти.

Регуляризация

Есть расширения обучения линейной модели, называемой методами регуляризации. Они направлены как на минимизацию суммы квадратов ошибки модели на обучающих данных (с использованием метода наименьших квадратов), но и на снижения сложности модели (например, количество или абсолютный размер суммы всех коэффициентов в модели).

Два популярных примера процедуры регуляризации линейной регрессии:

Лассо регрессия (Lasso Regression): метод наименьших квадратов модифицируются, чтобы также свести к минимуму абсолютную сумму коэффициентов (так называемая регуляризация L1).
Регрессия хребта (Ridge Regression): метод наименьших квадратов модифицируются, чтобы свести к минимуму квадрат абсолютной суммы коэффициентов (так называемая регуляризация L2).

Эти методы эффективны в использовании, когда есть коллинерность во входных данных и метод наименьших квадратов соответствует обучающим данным.

Теперь, когда вы знаете некоторые методы изучения коэффициентов в модели линейной регрессии, давайте посмотрим, как мы можем использовать модель для прогнозирования новых данных.

Прогнозирование с помощью с линейной регрессии

Учитывая, что представление является линейным уравнением, сделать прогнозы так же просто, как решение уравнения для определенного набора входов.

Рассмотрим конкретный пример. Представьте, что мы прогнозируем вес человека (y) в зависимости от высоты человека (x). Наше представление модели линейной регрессии для этой проблемы будет:

вес человека = B0 + B1 * высота человека

Где B0 является коэффициентом смещения, а B1 - коэффициентом для столбца высоты человека. Мы используем технику обучения, чтобы найти хороший набор значений коэффициентов. После того, как найдено, мы можем подключить различные значения высоты, чтобы предсказать вес.

Например, позволяет использовать B0 = 0,1 и B1 = 0,5. Давайте подставим их и рассчитаем вес (в килограммах) для человека с ростом 182 сантиметра.

вес человека = 0,1 + 0,5 * 182

вес человека = 91.1

Вы можете видеть, что вышеупомянутое уравнение может быть отображена как линия в двух измерениях. Коэффициент B0 является нашей отправной точкой независимо от того, какой рост у человека. Мы можем пробежать через различные высоту человека от 100 до 200 сантиметров подставив в уравнению и получить значения веса, создавая нашу линию.

Пример высоты против веса линейной регрессии

Теперь, когда мы знаем, как делать прогнозы с учетом выученной модели линейной регрессии, давайте посмотрим на некоторые правила для подготовки наших данных, чтобы максимально получить от этого типа модели.

Подготовка данных к линейной регрессии

Линейная регрессия изучается уже давно, и есть много литературы о том, как ваши данные должны быть структурированы, чтобы наилучшим образом использовать модель МНК или Градиентного спуска.

Таким образом, когда речь идет об этих требованиях и ожиданиях, они могут быть пугающими. Эти правила можно использовать скорее как практические правила при использовании алгоритмов линейной регрессии.

Используя эти эвристики и посмотреть, что лучше всего работает для вашей проблемы:

Линейные предпосылки. Линейная регрессия предполагает, что связь между входными и выходным данными является линейной. Линейная регрессия не поддерживает ничего другого. Это может быть очевидно, но это хорошо, чтобы помнить, когда у вас есть много атрибутов. Возможно, потребуется преобразовать данные, чтобы сделать отношения между ними линейными (например, логарифмическое преобразование для экспоненциальной связи).
Удалите шум. Линейная регрессия предполагает, что переменные на выходе и вывода не являются шумными. Рассмотрите возможность использования операций по очистке данных, которые позволяют лучше разоблачать и прояснять сигнал в данных. Это наиболее важно для переменной вывода, и, по возможности, необходимо удалить выбросы в переменной вывода (y).
Удалите коллинеарность. Линейная регрессия будет чрезмерно соответствовать вашим данным, когда у вас есть сильно коррелированные входные переменные. Рассмотрим расчет парных корреляций для входных данных и удаление наиболее коррелированных данных.
Гауcсово распределение. Линейная регрессия сделает более надежные прогнозы, если входные и выходные переменные имеют гауссово распределение. Вы можете получить некоторую выгоду с помощью преобразований (например, log или BoxCox) на переменных, чтобы сделать их распределение более гауссово.
Нормализованные входные данные: Линейная регрессия часто делает более надежные прогнозы, если отмасштабировать входные переменные с помощью стандартизации или нормализации.

Научим основам Python и Data Science на практике

Это не обычный теоритический курс, а онлайн-тренажер, с практикой на примерах рабочих задач, в котором вы можете учиться в любое удобное время 24/7. Вы получите реальный опыт, разрабатывая качественный код и анализируя реальные данные.

Читайте также: