История развития понятия чисел презентация кратко

Обновлено: 06.07.2024

3. Введение

Запись чисел шумерами
Первыми придумали запись чисел древние шумеры.
Они пользовались всего двумя цифрами. Вертикальная чёрточка обозначала
одну единицу, а угол из двух лежачих чёрточек – десять.
Эти чёрточки у них получались в виде клиньев, потому что они писали острой
палочкой на сырых глиняных дощечках, которые потом сушили.

Египетская нумерация
Одна из древнейших нумераций египетская. До нас дошли надписи,
сохранившиеся внутри пирамид, на плитах и обелисках.
Они состоят из картинок – иероглифов, которые изображают птиц, зверей,
людей, части человеческого тела (глаза, ноги) и различные неодушевленные предметы.
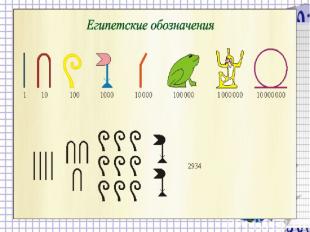
Для того, чтобы изобразить, например, целое число 23145,
достаточно записать в ряд два иероглифа.

Счет у племени майя
Очень интересная система счета была у народа Майя, который жил в
Центральной Америки. Можно лишь без конца изумляться великой мудрости народа,
сумевшего практически в одиночку подняться на недоступные вершины абстрактного
математического мышления.
Индейцы майя ухитрялись писать любое число, используя только точку и линию.

В течение многих столетий, переходя от народа к
народу, старинные индийские цифры много раз
изменялись, пока приняли современную форму.

Заключение
Со временем углы сгладились, и цифры приобрели привычный нам вид.
Вот уже много столетий весь мир пользуется арабской системой записи чисел.
Этими десятью знаками можно легко выразить огромные значения.
Зная историю прошлого, можно судить о необходимости
выражения чисел знаками и цифрами.

3 Учиться считать требовала жизнь Надо было знать, хватит ли добычи до следующей охоты, хватит ли пойманной рыбы? Самой древней математической деятельностью был счет. Счет был необходим, чтобы следить за поголовьем скота и вести торговлю. Некоторые первобытные племена подсчитывали количество предметов, соотнося их с различными частями тела, главным образом пальцами рук и ног. Наскальный рисунок, сохранившийся до наших времен от каменного века, изображает число 35 в виде серии выстроенных в ряд 35 палочек-пальцев.

4 А научившись считать по пальцам до десяти, люди стали считать десятками. Пальцы оказались прекрасной вычислительной машиной. С их помощью можно было считать до 5 Если взять две руки, то и до десяти В странах, где люди ходили босиком, по пальцам легко было считать до 20.

6 В Древнем Египте числа первого десятка записывали соответствующим количеством палочек Десять обозначалось скобочкой в виде подковы Сотню обозначали крючком Так обозначал и тысячу А так- миллион Сто тысяч обозначали лягушкой Но разве такая запись удобна?

7 В Древнем Вавилоне все числа составлялись из сочетаний клинышков. Вертикальная чёрточка обозначала одну единицу, а угол из двух лежачих чёрточек- десять Древневавилонский клинописный текст, содержащий перечень прямоугольных треугольников с рациональными сторонами (Плимптоновская библиотека Колумбийского университета) Древневавилонский клинописный текст. На изображенном участке содержится 16 задач с решениями, относящиеся к расчету плотин, валов, колодцев. Задача, снабженная чертежом, относится к расчету кругового вала. (Британский музей) Квадрат с диагоналями. Древневавилонский клинописный текст. (Из коллекции Йельского университета)

8 Египет Наше знание древнеегипетской математики основано главным образом на двух папирусах, датируемых примерно 1700 до н.э. Излагаемые в этих папирусах математические сведения восходят к еще более раннему периоду – около 3500 до н.э. Египтяне использовали математику, чтобы вычислять вес тел, площади посевов и объемы зернохранилищ, размеры податей и количество камней, требуемое для возведения тех или иных сооружений. В папирусах можно найти также задачи, связанные с определением количества зерна, необходимого для приготовления заданного числа кружек пива, а также более сложные задачи, связанные с различием в сортах зерна. Древнеегипетская письменность основывалась на иероглифах. Система счисления того периода также уступала вавилонской. Египтяне пользовались непозиционной десятичной системой, в которой числа от 1 до 9 обозначались соответствующим числом вертикальных черточек, а для последовательных степеней числа 10 вводились индивидуальные символы. Последовательно комбинируя эти символы, можно было записать любое число. С появлением папируса возникло так называемое иератическое письмо-скоропись, способствовавшее, в свою очередь, появлению новой числовой системы. Для каждого из чисел от 1 до 9 и для каждого из первых девяти кратных чисел 10, 100 и т.д. использовался специальный опознавательный символ. Дроби записывались в виде суммы дробей с числителем, равным единице. С такими дробями египтяне производили все четыре арифметические операции, но процедура таких вычислений оставалась очень громоздкой.

9 Фрагмент кожаного свитка, содержащего перечень простых соотношений между дробями. Найден вблизи заупокойного храма Рамзеса II в Фивах. Датируется примерно 1700 г. до н.э. (Британский музей) Изображение на могиле Джесеркере-сонб в Фивах (Верхний Египет). Датируется 1567–1310 гг. до н.э. На верхней части изображена процедура установления границ земельных участков. Характерно, что математические знания египтян, носящие форму рецептов для решения практических задач, развиваются параллельно с требованием в искусстве пытаться дать возможно наиболее детальное воспроизведение изображаемого предмета

10 Запись чисел в Древней Руси титло Славянские цифровые знаки- буквы с титлами

11 ГРЕЧЕСКАЯ МАТЕМАТИКА Многие считают, что родоначальниками математики явились греки классического периода (6–4 вв. до н.э.). Математика, существовавшая в более ранний период, была набором эмпирических заключений. Напротив, в дедуктивном рассуждении новое утверждение выводится из принятых посылок способом, исключавшим возможность его неприятия. Настаивание греков на дедуктивном доказательстве было экстраординарным шагом. Ни одна другая цивилизация не дошла до идеи получения заключений исключительно на основе дедуктивного рассуждения, исходящего из явно сформулированных аксиом. Одно из объяснений приверженности греков методам дедукции мы находим в устройстве греческого общества классического периода. Математики и философы (нередко это были одни и те же лица) принадлежали к высшим слоям общества, где любая практическая деятельность рассматривалась как недостойное занятие. Математики предпочитали абстрактные рассуждения о числах и пространственных отношениях решению практических задач. Математика делилась на арифметику – теоретический аспект и логистику – вычислительный аспект. Заниматься логистикой предоставляли свободнорожденным низших классов и рабам. Дедуктивный характер греческой математики полностью сформировался ко времени Платона и Аристотеля. Изобретение дедуктивной математики принято приписывать Фалесу Милетскому (ок. 640–546 до н.э.), который, как и многие древнегреческие математики классического периода, был также философом. Высказывалось предположение, что Фалес использовал дедукцию для доказательства некоторых результатов в геометрии, хотя это сомнительно.

15 Знаменательной вехой в алгебре александрийских греков стали работы Диофанта (ок. 250). Одно из главных его достижений связано с введением в алгебру начал символики. В своих работах Диофант не предлагал общих методов, он имел дело с конкретными положительными рациональными числами, а не с их буквенными обозначениями. Он заложил основы так называемого диофантова анализа – исследования неопределенных уравнений.

16 Высшим достижением александрийских математиков стало создание количественной астрономии. Гиппарху (ок. 161–126 до н.э.) мы обязаны изобретением тригонометрии. Его метод был основан на теореме, утверждающей, что в подобных треугольниках отношение длин любых двух сторон одного из них равно отношению длин двух соответственных сторон другого. В частности, отношение длины катета, лежащего против острого угла А в прямоугольном треугольнике, к длине гипотенузы должно быть одним и тем же для всех прямоугольных треугольников, имеющих один и тот же острый угол А. Это отношение известно как синус угла А. Отношения длин других сторон прямоугольного треугольника получили название косинуса и тангенса угла А. Гиппарх изобрел метод вычисления таких отношений и составил их таблицы. Располагая этими таблицами и легко измеримыми расстояниями на поверхности Земли, он смог вычислить длину ее большой окружности и расстояние до Луны. По его расчетам, радиус Луны составил одну треть земного радиуса; по современным данным отношение радиусов Луны и Земли составляет 27/1000. Гиппарх определил продолжительность солнечного года с ошибкой всего лишь в 61/2 минуты; считается, что именно он ввел широты и долготы.

17 ИНДИЯ Ибн аль-Хайсам Махавира (850 н.э.) установил правила операций с нулем, полагая, однако, что деление числа на нуль оставляет число неизменным. Правильный ответ для случая деления числа на нуль был дан Бхаскарой (р. в 1114), ему же принадлежат правила действий над иррациональными числами. Индийцы ввели понятие отрицательных чисел (для обозначения долгов). Самое раннее их использование мы находим у Брахмагупты (ок. 630). Ариабхата (р. 476) пошел дальше Диофанта в использовании непрерывных дробей при решении неопределенных уравнений. Преемниками греков в истории математики стали индийцы. Индийские математики не занимались доказательствами, но они ввели оригинальные понятия и ряд эффективных методов. Именно они впервые ввели нуль и как кардинальное число, и как символ отсутствия единиц в соответствующем разряде.

18 НАЧАЛО СОВРЕМЕННОЙ МАТЕМАТИКИ Наступление 16 в. в Западной Европе ознаменовалось важными достижениями в алгебре и арифметике. Были введены в обращение десятичные дроби и правила арифметических действий с ними. Исаак НьютонК. Фридрих Гаусс Н. Абель

19 Математический анализ. Основатели современной науки Галилео Галилей Иоганн Кеплер Николай Коперник

20 Готфрид Вильгельм Лейбниц Иоганн Бернулли Николай Иванович Лобачевский

22 Это лишь малая капля из истории развития математики, огромного мира ЧИСЕЛ. Надо самостоятельно изучать этот огромный и неведомый Океан тайн чисел. Надо отправляться в этот Океан так, как это делали первые аргонавты планеты или первые космонавты Земли. Надо учиться вязать плоты из лёгких и изученных цифр, строгать вёсла, шить цифровые паруса, изучать числовые приливы и отливы, мели и глубины числовых бездн и становиться, наконец, НАСТОЯЩИМИ ЧИСЛОНАВТАМИ.

24 Информационные ресурсы Большая советская энциклопедия Энциклопедический словарь юного математика Картинки, использованные в презентации, с сайта:

№ слайда 1

Тема: Развитие понятия о числе Талица 2015 Государственное бюджетное профессиональное образовательное учреждение Свердловской области «Талицкий лесотехнический колледж им. Н.И.Кузнецова Выполнила преподаватель Кудина Л.В.

№ слайда 2

В результате изучения темы студент должен уметь выполнять преобразования с действительными числами. В результате изучения студенты должны знать: -Понятие натуральных, целых и рациональных чисел. - Понятие иррационального числа. - Понятие действительных чисел.

№ слайда 3

Из истории чисел Возникнув еще в первобытном обществе из потребностей счета, понятие числа с развитием науки значительно расширилось. . На первых этапах существования человеческого общества числа, открытые в процессе человеческой деятельности, служили для примитивного счета предметов, дней, шагов и т.п. Число- основное понятие математики, используемое для количественной характеристики, сравнения, нумерации объектов и их частей. Письменными знаками для обозначения чисел служат цифры, а также символы математических операций.

№ слайда 4

№ слайда 5

Из истории чисел . На этом развитие не завершилось. В связи с решением уравнений математики встречались с числом, которое выражалось . Первая дробь, с которой познакомились люди, была, наверное, половина. За ней последовали ¼, 1/8, …, затем 1/3, 1/6 и т.д., то есть самые простые дроби, у них числитель всегда единица. Лишь значительно позже у греков, затем у индейцев и других народов стали входить в употребление и дроби общего вида, называемые обыкновенными, у которых числитель и знаменатель могут быть любыми натуральными числами. В дальнейшем оказалось необходимым еще более расширить понятие числа. Последовательно появились числа иррациональные, отрицательные и комплексные.

№ слайда 6

№ слайда 7

№ слайда 8

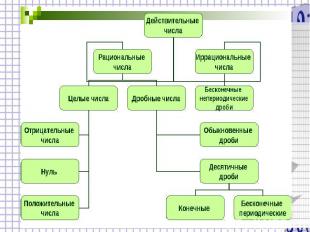
Натуральные числа Натуральные числа (естественные числа) – числа, возникающие естественным образом при счёте (как в смысле перечисления, так и в смысле исчисления). Множество всех натуральных чисел принято обозначать знаком N. Множество натуральных чисел является бесконечным, так как для любого натурального числа найдётся большее его натуральное число.

№ слайда 9

Операции над натуральными числами К замкнутым операциям (операциям, не выводящим результат из множества натуральных чисел) над натуральными числами относятся следующие арифметические операции: Сложение. Слагаемое + Слагаемое = Сумма Умножение. Множитель * Множитель = Произведение Возведение в степень , ab где a — основание степени и b — показатель степени. Если основание и показатель натуральны, то и результат будет являться натуральным числом. Дополнительно рассматривают ещё две операции. С формальной точки зрения они не являются операциями над натуральными числами, так как не определены для всех пар чисел (иногда существуют, иногда нет). Вычитание. Уменьшаемое Вычитаемое = Разность. При этом Уменьшаемое должно быть больше Вычитаемого (или равно ему, если считать 0 натуральным числом). Деление. Делимое / Делитель = (Частное, Остаток).

№ слайда 10

Целые числа – бывают положительными и отрицательными. Совокупность целых чисел образует множество целых чисел. Число вида а/в, где а и b целые числа, причём называется рациональным числом. Множество, состоящее из положительных и отрицательных дробных чисел, называется множеством рациональных чисел.

№ слайда 11

Основные свойства Коммутативность сложения. A+B=B+A Коммутативность умножения. A.B=B.A Ассоциативность сложения. (A+B)+C=A+(B+C) Ассоциативность умножения. (AB)C=A(BC) Дистрибутивность умножения относительно сложения.

№ слайда 12

Числовые множества Обозначение Название множества N Множество натуральных чисел Z Множество целых чисел Q=m/n Множество рациональных чисел I=R/Q Множество иррациональных чисел R Множество вещественных чисел

№ слайда 13

№ слайда 14

№ слайда 15

Математический диктант 1 вариант 2 вариант n = 8 x = 9 a = 323 y = 108 z = 749 n = 6 x = 9 a = 349 y = 117 z = 837 Проверьте себя:

№ слайда 16

Любое рациональное число можно представить либо в виде конечной десятичной дроби, либо в виде бесконечной периодической десятичной дроби. Выполнить действия: 1. 2.

№ слайда 17

Периодические дроби. Определение: Периодические дроби бывают чистыми и смешанными. Чистой периодической называется дробь, у которой период сразу после запятой. . Смешанной называется дробь, у которой между запятой и первым периодом есть одна или несколько повторяющихся цифр: . 142857)

№ слайда 18

. Обращение смешанной периодической дроби в обыкновенную: Чтобы обратить смешанную периодическую дробь достаточно из числа стоящего до второго периода вычесть число стоящее до первого периода, и полученную разность взять числителем , а знаменателем написать цифру в периоде столькими нулями сколько цифр между запятой и периодом:

№ слайда 19

№ слайда 20

Геометрическая интерпретация комплексного числа

№ слайда 21

Комплексные взаимносопряженные числа Z=А - В i сопряженное Z= А + В i Комплексные числа называются взаимно сопряженными, если их действительные части равны, а мнимые отличаются знаками

№ слайда 22

Модуль комплексного числа Комплексные взаимносопряженные числа Z=А - В i сопряженное Z= А + В i Z = A + B i

№ слайда 23

Выполните сложение комплексных чисел

№ слайда 24

Найдите разность комплексных чисел: ответ ответ ответ ответ ответ

№ слайда 25

Найдите произведение комплексных чисел:

№ слайда 26

Выполните действия: 1. 2. 3. 4. 5.

№ слайда 27

Вычислите: 1. 2. 3. 5. 4.

№ слайда 28

Работа в парах I вариант 1)Приведите пример целого числа. 2)Какие числа называются целыми? 3)Какие числа называются иррациональными? 4)Докажите, что 5-рациональное число. II вариант 1) Приведите пример рационального числа. 2)Какие числа называются рациональными? 3) Какие числа называются действительными? 4)Докажите, что -2/5 действительное число.

№ слайда 29

№ слайда 30

№ слайда 31

Помогите другим пользователям — будьте первым, кто поделится своим мнением об этой презентации.

Аннотация к презентации

Содержание

Тема: Развитие понятия о числе

Талица 2015 Государственное бюджетное профессиональное образовательное учреждение Свердловской области «Талицкий лесотехнический колледж им. Н.И.Кузнецова Выполнила преподаватель Кудина Л.В.

Слайд 2

Слайд 3

Из истории чисел

Возникнув еще в первобытном обществе из потребностей счета, понятие числа с развитием науки значительно расширилось. . На первых этапах существования человеческого общества числа, открытые в процессе человеческой деятельности, служили для примитивного счета предметов, дней, шагов и т.п. Число- основное понятие математики, используемое для количественной характеристики, сравнения, нумерации объектов и их частей. Письменными знаками для обозначения чисел служат цифры, а также символы математических операций.

Слайд 4

Слайд 5

. На этом развитие не завершилось. В связи с решением уравнений математики встречались с числом, которое выражалось . Первая дробь, с которой познакомились люди, была, наверное, половина. За ней последовали ¼, 1/8, …, затем 1/3, 1/6 и т.д., то есть самые простые дроби, у них числитель всегда единица. Лишь значительно позже у греков, затем у индейцев и других народов стали входить в употребление и дроби общего вида, называемые обыкновенными, у которых числитель и знаменатель могут быть любыми натуральными числами. В дальнейшем оказалось необходимым еще более расширить понятие числа. Последовательно появились числа иррациональные, отрицательные и комплексные.

Слайд 6

Слайд 7

Слайд 8

Слайд 9

Операции над натуральными числами К замкнутым операциям (операциям, не выводящим результат из множества натуральных чисел) над натуральными числами относятся следующие арифметические операции: Сложение. Слагаемое + Слагаемое = Сумма Умножение.Множитель * Множитель = Произведение Возведение в степень , ab где a — основание степени и b — показатель степени. Если основание и показатель натуральны, то и результат будет являться натуральным числом. Дополнительно рассматривают ещё две операции. С формальной точки зрения они не являются операциями над натуральными числами, так как не определены для всех пар чисел (иногда существуют, иногда нет). Вычитание.Уменьшаемое Вычитаемое = Разность. При этом Уменьшаемое должно быть больше Вычитаемого (или равно ему, если считать 0 натуральным числом). Деление.Делимое / Делитель = (Частное, Остаток).

Слайд 10

Слайд 11

Слайд 12

Слайд 13

Слайд 14

Слайд 15

Математический диктант 1 вариант 2вариант 56 = 7  n 1. n = 8 72 : x = 8 2. x = 9 723 –a = 400 3. a = 323 y : 27 = 4 4. y = 108 z + 251 = 1000 5. z = 749 n = 6 81 : x = 9 2. x = 9 549 – a = 200 3. a = 349 y : 39 = 3 4. y = 117 z + 163 = 1000 5. z = 837 1. 48 = 8 n Проверьте себя: