Имитационное моделирование метод монте карло кратко

Обновлено: 04.07.2024

Моделирование методом Монте-Карло имеет множество применений в финансовой практике, связанных с анализом сложных случайных процессов, в том числе в финансовом планировании, стоимостной оценке рисков (VaR), оценке стоимости сложных опционов и других финансовых активов. Рассмотрим концепцию моделирования методом Монте-Карло в рамках изучения количественных методов по программе CFA.

Разобравшись в основах распределений вероятности, мы теперь готовы узнать о компьютерном методе, в котором вероятностные распределения играют важную роль. Этот метод называется моделированием методом Монте-Карло, статистическим моделированием или имитационным моделированием (англ. 'Monte Carlo simulation').

Моделирование методом Монте-Карло в области финансов предполагает использование компьютера для имитации функционирования сложной финансовой системы.

Характерной особенностью моделирования методом Монте-Карло является генерация большого числа случайных выборок из заданного распределения вероятностей или распределений, характеризующих риск в рассматриваемой системе.

Моделирование методом Монте-Карло имеет несколько совершенно разных применений. Один из вариантов использования - в финансовом планировании.

Исследователь Стэнфордского университета Сэм Сэведж представил следующую довольно точную аналогию роли этого метода:

Так же, как встряхивание лестницы помогает нам оценить риски падения с лестницы, моделирование методом Монте-Карло позволяет экспериментировать с предлагаемой финансовой стратегией или политикой до ее фактического осуществления. Например, показатели инвестиционной деятельности можно оценить относительно эталона или обязательства.

Пенсионные планы с установленными выплатами часто предполагают вложение свободных активов в зависимости от запланированного погашения пенсионных обязательств.

Пенсионные обязательства представляют собой сложный случайный процесс. В финансовом планировании активов и обязательств с использованием метода Монте-Карло, функционирование пенсионных активов и обязательств моделируется на определенный временной период, с учетом допущений о том, как инвестируются активы и других случайных величин.

Ключевым моментом в этой имитации и методе Монте-Карло является распределение вероятностей для различных источников риска (в том числе процентных ставок и ставок доходности рынка ценных бумаг, в данном случае).

Последствия решений инвестиционной политики пенсионного фонда можно оценить с помощью моделирования на определенный период. Эксперимент можно повторить для другого набора допущений.

В приведенном ниже Примере (11) серия ставок доходности не достаточно велика, чтобы ответить на вопросы аналитиков о временных закономерностях фондового рынка, поэтому исследователи моделируют рыночную доходность, чтобы найти ответы на свои вопросы.

Моделирование методом Монте-Карло также широко используется для получения стоимостной оценки риска VaR. В этом случае мы моделируем показатель прибыли и убытков портфеля в течение определенного промежутка времени.

Повторные испытания в рамках моделирования (каждое испытание означает получение случайных наблюдений из распределения вероятностей) создают частотное распределение для оценки стоимости портфеля. Например, точка, которая определяет порог отсечения, по меньшей мере, 5% благоприятных моделируемых изменений, является 95%-ной оценкой риска VaR.

Чрезвычайно важным применением моделирования методом Монте-Карло является оценка сложных ценных бумаг, в частности, некоторых европейских опционов, для которых не существует аналитической формулы ценообразования.

Опцион в европейском стиле или европейский опцион (англ. 'European-style option') может быть исполнен только по истечении определенного срока.

Для других ценных бумаг, таких как ипотечные ценные бумаги со сложными встроенными опционами, моделирование методом Монте-Карло также является важным аналитическим инструментом.

Исследователи используют моделирование методом Монте-Карло, чтобы проверить свои модели и инструменты.

Насколько критично конкретное предположение об эффективности модели?

Поскольку мы управляем предположениями, когда делаем имитацию, мы можем выполнить моделирование методом Монте-Карло, чтобы исследовать чувствительность модели к изменению наших предположений.

Процесс моделирования методом Монте-Карло.

Чтобы понять технику моделирования методом Монте-Карло, давайте представим процесс в виде серии шагов.

Эти шаги следует рассматривать только с целью изучения метода Монте-Карло, а не в качестве подробного рецепта для практической работы с этим методом, так как процесс может сильно отличаться в зависимости от области его применения, которая также очень разнообразна.

Для того, чтобы проиллюстрировать эти шаги, мы рассмотрим пример использования метода Монте-Карло для оценки азиатского колл-опциона, не имеющего аналитической формулы ценообразования.

Азиатский колл-опцион (англ. 'Asian call option') - это опцион в европейском стиле со стоимостью в момент исполнения, равной разнице между ценой акций в момент исполнения и средней ценой акций в течение срока действия опциона, или $0, в зависимости от того, что больше.

Например, если цена акции в момент исполнения опциона составляет $34, а средняя стоимость в течение срока действия опциона составляет $31, то стоимость опциона на момент исполнения составляет $3 (наибольшее значение из $34 - $31 = $3 и $0).

Шаги с 1 по 3 описывают имитацию;
Шаги с 4 по 7 выполняют сам процесс имитации.

Шаг 1. Определите интересующие величины (стоимость опциона, например, или размер активов пенсионного плана) в терминах базовых случайных величин.

Базовой случайной величиной (или несколькими величинами) может быть цена акций опциона, рыночная стоимость пенсионных активов, или другие случайные величины, связанные с обязательствами по пенсионному плану.

Укажите первоначальные значения базовых случайных величин.

Для иллюстрации шагов, мы используем оценку азиатского колл-опциона: $ С_ $ представляет стоимость опциона при исполнении в момент времени $T$. Нижний индекс $i$ в $ С_ $ указывает, что значение $ С_ $ является результатом $i-\text$ имитационного испытания (англ. 'simulation trial').

Каждое имитационное испытание требует генерации случайной величины (итерация Шага 4).

Шаг 2. Определите временную шкалу. Возьмите календарный временной горизонт и разделить его на несколько подпериодов, общим числом $K$.

Календарный период разделенный на $K$ подпериодов, имеет временной инкремент (приращение времени) $\Delta t$.

Шаг 3. Сделайте предположения о характере распределения для факторов риска, которые влияют на базовые случайные величины.

Например, цена акций является базовой случайной величиной для азиатского колл-опциона, поэтому нам нужна модель движения цен на акции. Допустим, мы выбираем следующую модель движения цен на акции, где $ Z_k $ обозначает стандартную нормальную случайную величину:

$\Delta t$(Цена акций) = ($ \mu \times $ Предыдущая цена акций $\times \Delta t$) + ($ \sigma \times $ Предыдущая цена акций $\times Z_k $)

В данном случае, $ Z_k $ является фактором риска при моделировании. Выбирая значение $ \mu$ и $ \sigma$, мы контролируем распределение стоимости акций. Хотя в этом примере используется один фактор риска, данная имитация может иметь несколько факторов риска.

Шаг 4. С помощью компьютерной программы или функции Excel, сгенерируйте $K$ случайные наблюдения для каждого фактора риска.

В нашем примере, функция Excel будет генерировать $K$ значений стандартной нормальной случайной величины $ Z_k $: $ Z_1, \ Z_2, \ Z_3, \ldots , \ Z_k $.

Шаг 5. Вычислите базовые случайные величины, используя случайные наблюдения, сгенерированные на Шаге 4.

Результатом описанной выше модели динамики цены акций будет $K$ наблюдений изменений цены акций. Для преобразования этих изменений в $K$ цен на акции необходим дополнительный расчет (с использованием первоначальных цен акций, определенных на Шаге 1).

Другой расчет вычисляет среднюю цену акций в течение срока действия опциона (т.е. сумма $K$ цен на акции делятся на $K$).

Шаг 6. Рассчитайте интересующие величины.

В нашем примере, первый расчет определяет стоимость азиатского колл-опциона на момент исполнения, $ С_ $. А второй расчет дисконтирует эту конечную (будущую) стоимость к приведенной (текущей) стоимости, чтобы получить стоимость опциона на текущую дату, $ С_ $.

Мы выполнили одно имитационное испытание (Нижний индекс $i$ в $ С_ $ означает $i-\text$ имитационное испытание).

При моделировании методом Монте-Карло, в табличной форме записываются статистические данные каждого испытания, касающиеся распределения интересующих нас величин, в том числе их средние значения и стандартные отклонения.

Шаг 7. Итеративно возвращайтесь к Шагу 4, пока не выполните все $ I $ испытаний.

И, наконец, рассчитайте итоговые статистические данные для всех имитаций. Ключевым значением в нашем примере является среднее значение $ С_ $ для общего количества имитационных испытаний, $ I $. Это среднее значение и будет оценкой стоимости азиатского колл-опциона методом Монте-Карло.

Сколько имитационных испытаний необходимо выполнить?

Как правило, нам нужно увеличить количество испытаний на коэффициент 100, чтобы увеличить точность испытания на 1 знак.

В зависимости от задачи, могут потребоваться десятки тысяч испытаний, чтобы получить точность до 2 знаков после запятой (например, это требуется стоимости опциона).

Проведение большого количества испытаний не обязательно проблематично, учитывая нынешние вычислительные мощности (даже обычного пользовательского ПК). Необходимое число имитационных испытаний может быть уменьшено с использованием специальных процедур понижения дисперсии, но эта тема выходит за рамки данного чтения.

Для получения дополнительной информации об уменьшении числа испытаний и о других технических аспектах моделирования методом Монте-Карло, см. Hillier and Lieberman (2010).

Генераторы случайных чисел и процедура генерации случайных наблюдений.

На Шаге 4 нашего примера, компьютер генерирует набор случайных наблюдений для стандартной нормальной случайной величины. Напомним, что для равномерного распределения все возможные исходы равновероятны.

Из-за этой предсказуемости, технически правильное название для чисел, полученных с помощью генераторов случайных чисел - псевдослучайные числа (англ. 'pseudo-random numbers').

Замечательным фактом является то, что случайные наблюдения из любого распределения можно получить с использованием равномерной случайной величины в диапазоне от 0 до 1.

Для того, чтобы лучше понять это, рассмотрим метод обратной трансформации случайных наблюдений (англ. 'inverse transformation method').

Предположим, что мы заинтересованы в получении случайных наблюдений для случайной величины $X $, с кумулятивной функцией распределения $ F(x) $. Напомним, что $ F(x) $, рассчитанная в точке $x$, представляет собой число между 0 и 1.

Предположим, что случайный исход этой случайной величины равен 3.21 и что $F(3.21) = 0.25$ или 25%.

Определим обратную функцию $F$ и назовем ее $ F^ $. Она может сделать следующее: подставим вероятность 0.25 в функцию $ F^ $, и она вернет случайный результат 3.21. Другими словами, $ F^(0.25)=3.21 $.

Для генерации случайных наблюдений величины $ X $, выполняются следующие шаги:

генерация равномерного случайного числа $r$, между 0 и 1, с использованием генератора случайных чисел и
расчет $ F^(r) $, чтобы получить случайное наблюдение величины $ X $.

Генерация случайного наблюдения сама по себе является областью отдельного изучения, и здесь мы лишь кратко обсудили метод обратной трансформации.

Как финансовому аналитику, вам не придется заниматься техническими деталями преобразования случайных чисел в случайные наблюдения, но вы должны знать, что случайные наблюдения из любого распределения можно сгенерировать с использованием равномерной случайной величины.

Далее, в Примерах 11 и 12, мы проиллюстрируем, как моделирование методом Монте-Карло позволяет определить потенциальную выгоду от выбора момента сделки (рыночного тайминга).

Пример (11) определения потенциальной прибыли от рыночного тайминга: метод Монте-Карло (1).

Все активные инвесторы хотят достичь наилучшей эффективности. Одним из возможных источников высокой эффективности является выбор момента сделки или рыночный тайминг (англ. 'market timing') - способность определить оптимальный момент для покупки или продажи ценных бумаг.

Насколько точно инвестор должен прогнозировать бычий рынок (англ. 'bull market') и медвежий рынок (англ. 'bear market'), чтобы получать прибыль?

Из-за большой изменчивости доходности активов, необходим огромный объем данных о доходности, чтобы получить статистически достоверные ответы на эти вопросы.

Поэтому исследователи Chua, Woodward и To (1987) выбрали метод Монте-Карло для определения потенциальной прибыли от рыночного тайминга. Их интересовали перспективы канадских инвесторов.

Чтобы понять их исследование, предположим, что в начале года инвестор прогнозирует, что в следующем году будет либо бычий рынок, либо медвежий рынок.

Если прогнозируется бычий рынок, инвестор вкладывает все свои деньги в акции и получает рыночную доходность за этот год.
С другой стороны, если прогнозируется медвежий рынок, инвестор вкладывает деньги в казначейские векселя и получает безрисковую доходность.

Рынок классифицируется как бычий, если рыночная доходность $ R_$ за вычетом безрисковой доходности по казначейским векселям $ R_$, является положительной в течение года. В противном случае, рынок классифицируются как медвежий рынок.

Инвестиционные результаты тех, кто использует рыночный тайминг можно сравнить с результатами тех, кто придерживается долгосрочной стратегии buy-and-hold. Долгосрочный инвестор получает рыночный доход ежегодно.

Для Chua и др. одним из интересующих показателей был выигрыш от рыночного тайминга. Они определили эту величину как среднюю доходность маркет-таймера за вычетом средней доходности долгосрочного инвестора.

Чтобы сымитировать рыночную доходность, Chua и др. сгенерировали 10 000 случайных стандартных нормальных наблюдений, $ Z_t $. Во время исследования средняя годовая доходность канадских акций составляла 12.95%, а стандартное отклонение - 18.30%.

С учетом этих параметров, моделируемая рыночная доходность будет:

$ R_ = 0.1830 Z_t + 0.1295, \ t = 1, \ 2, \ \ldots, \ 10,000. $

Используя второй набор 10 000 случайных стандартных нормальных наблюдений, историческую доходность канадских казначейских векселей, а также историческую корреляцию векселей и доходности акций, авторы сгенерировали 10 000 ставок доходности казначейских векселей.

Инвесторы могут обладать различными навыками и опытом прогнозировании бычьих и медвежьих рынков. Chua и др. охарактеризовали маркет-таймеров по точности прогнозирования бычьих рынков и точности прогнозирования медвежьих рынков.

Например, точность прогнозирования бычьего рынка в 50% означает, что, если маркет-таймер прогнозирует бычий рынок на следующий год, он оказывается прав только в половине случаев, что указывает на отсутствие навыка.

Предположим, что точность в прогнозировании бычьего рынка составляет 60% и 80% - в прогнозировании медвежьего рынка (обозначается как 'маркет-таймер 60-80').

Мы можем смоделировать, насколько инвестор будет точен.

После генерации первого наблюдения для $ R_ - R_$, мы знаем, соответствует ли это наблюдение бычьему или медвежьему рынку.

Если наблюдение соответствует бычьему рынку, то 0.60 (точность прогноза на бычьем рынке) сравнивается со случайным числом (от 0 до 1).

Если случайное число оказывается меньше, чем 0.60, что происходит с вероятностью 60%, то предполагается, что маркет-таймер правильно предсказал бычий рынок и его доходность для этого первого наблюдения является рыночной ставкой доходности.

Если случайное число оказывается больше, чем 0.60, то предполагается, что маркет-таймер допустил ошибку и предсказал медвежий рынок. Его доходность для этого наблюдения является безрисковой ставкой доходности.

Аналогичным образом, если это первое наблюдение соответствует медвежьему рынку, маркет-таймер имеет 80-процентный шанс быть правым в прогнозировании медвежьего рынка на основе генерации случайных чисел.

В любом случае, доходность инвестора сравнивается с рыночной доходностью, чтобы зафиксировать его выигрыш (разницу) по сравнению с долгосрочной стратегией buy-and-hold.

Описанный выше процесс является одним имитационным испытанием (итерацией).

Сымитированной средней доходностью, заработанной маркет-таймером, будет средняя заработанная доходность по итогу всех испытаний в моделировании.

Для того, чтобы лучше понять этот процесс, рассмотрим гипотетическое моделирование методом Монте-Карло с четырьмя испытаниями для маркет-таймера 60-80 таймера (напомним, что это означает 60% точность в прогнозировании бычьих рынков и 80% точность в прогнозировании медвежьих рынков).

В Таблице 8 приведены данные для моделирования.

Давайте взглянем на испытания 1 и 2.

В испытании 1, первое сгенерированное случайное число приводит к рыночной доходности 0.121. Поскольку рыночная доходность 0.121, превысила безрисковую доходность по векселю 0.050, мы имеем дело с бычьим рынком.

Затем мы генерируем случайное число 0.531, которое мы потом сравниваем с точностью маркет-таймера для бычьего рынка, 0.60. Поскольку 0.531 меньше, чем 0.60, то предполагается, что маркет-таймер правильно спрогнозировал бычий рынок и, соответственно, вложился в акции. Таким образом, в этом испытании маркет-таймер получает рыночную доходность 0.121.

В испытании 2 мы наблюдаем еще один бычий рынок, и, поскольку случайное число 0.725 больше, чем 0.60, то предполагается, что маркет-таймер сделал ошибку и предсказал медвежий рынок. Таким образом, таймер заработал безрисковую доходность 0.081, а не более высокую рыночную доходность.

Финансовая грамотность

Метод Монте Карло используется для решения различных задач, где результат зависит от случайных процессов. В частности, метод широко используется в экономике, инвестиционных прогнозах и инвестиционном анализе, финансовом планировании. Моделирование по методу Монте Карло позволяет вычислить множество значений. Используя эти значения, определяется искомый результат путем вычисления среднего арифметического или диапазон, в котором может находиться нужный результат.

В этой статье мы расскажем, как применяется метод Монте Карло в экономике, личных финансах и инвестировании. С помощью наглядных примеров попытаемся понять, какие задачи можно решать с применением метода Монте Карло.

Что такое метод Монте Карло (ММК)

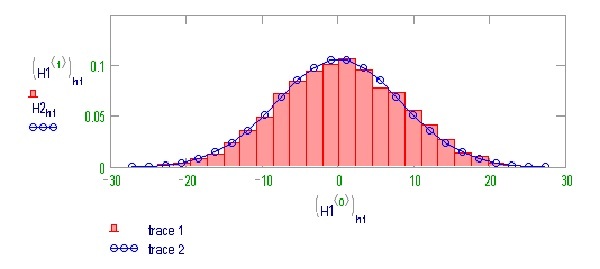
Итак, метод Монте Карло позволяет рассчитать какую-либо величину (или диапазон значений) с использованием множества случайных величин.

К примеру, бегун способен пробежать дистанцию в 10 км за 50 мин. Означает ли это, что 20 км он пробежит за 1 час 40 минут? Конечно же, нет: человек – не машина. Если 10 км можно пробежать без остановки, то расстояние вдвое больше требует значительных затрат энергии. Так, необходимо замедлиться, чтобы попить воды, завязать шнурки. При сильном учащении пульса – перейти на шаг или легкий бег и т.д.

Таким образом, прогнозирование времени путем простых математических расчетов – способ, который даст весьма неточный результат. Правильнее будет отобрать в случайном порядке результаты забегов нескольких спортсменов (чем больше, тем лучше) такого же пола, примерно того же возраста и уровня подготовки, которые несколько раз бежали дистанции по 20 км, и вычислить среднее арифметическое результатов. Тогда мы получим значение, на которое можно ориентироваться.

Поэтому следует ориентироваться только на имеющиеся данные, полученные в результате коллективных забегов, когда имели место подобные случаи. Выбрав несколько результатов и сопоставив их с количеством бегунов, пробежавших дистанцию успешно, мы получим средний процент риска.

Для прогнозирования рисков, доходности, сроков окупаемости и других финансовых результатов используется метод Монте-Карло-симуляции. Вероятность события определяется так: программа выбирает комбинации случайных значений (например, неблагоприятных исходов) и на основании этого выдает усредненный результат. Для получения более точного значения симуляцию следует повторить несколько раз. Программное обеспечение применяется различное – от знакомого нам всем Excel до узкоспециализированных программных продуктов, используемых финансовыми аналитиками, физиками, программистами, трейдерами и др.

История

Откуда метод получил свое название? В Европе есть маленькое княжество Монако, где одна из территорий названа Монте-Карло. Это такой европейский Лос-Анджелес, где можно окунуться в роскошь и азартные развлечения. От знаменитого казино метод Монте-Карло получил свое имя.

Впервые о методе заговорили в конце 40-х годов прошлого столетия, когда ВВС США начало разработку водородной бомбы. Тогда, с появлением первых ЭВМ, было предложено использовать теорию вероятностей для решения прикладных задач.

Далее, в 1970-х годах, метод получил применение в нейтронной физике для задач, не поддающихся решению традиционными математическими методами. Впоследствии моделирование по методу Монте-Карло распространилось на другие области физики, а также на экономику и вычислительную математику.

Схема метода

Имитационное моделирование по методу Монте-Карло представляет собой определение математического ожидания (среднего значения случайной величины) путем проведения определенного количества симуляций (испытаний).

Предположим, требуется найти математическое ожидание α для случайной величины $ X $ :

Классическая формула расчета математического ожидания выглядит так:

$ x1…n $ – значение величины от 1 до n;

$ p1…n $ – вероятность от 1 до n.

Моделирование методом Монте-Карло выполняется следующим образом: проводится n симуляций (испытаний). В результате получится какое-то количество значений X. Далее определяется их среднее арифметическое, которое и будет приблизительным значением α.

Зачем нужен ММК и где он применяется

Чтобы не углубляться в математические дебри, сформулируем кратко суть метода.

Метод Монте-Карло относится к методам моделирования различных явлений, событий, параметров или процессов, как благоприятных, так и неблагоприятных, с целью определения вероятности их наступления. Для этого генерируется определенное количество случайных величин, отвечающих установленным критериям, а затем на их основе вычисляют приблизительное значение искомой величины.

ММК применяется в следующих областях:

Физика, химия, биология – для моделирования различных явлений.
Экономика и финансы – для оценки и прогнозирования инвестиций, расчета доходности финансовых инструментов, сроков окупаемости и др. Метод Монте-Карло широко применяется для оценки рисков;
Игровая индустрия – для моделирования искусственного интеллекта и др.
Технология и др. инженерные науки используют метод Монте-Карло в прогнозировании НТП.
Социология – для изучения общественного мнения (люди, принимающие участие в опросах, отбираются в случайном порядке).

По сути, методу можно найти применение во многих сферах, где необходимы расчеты и прогнозирование.

Данные для получения искомой величины определяются путем стохастической (случайной) выборки. Чтобы было более понятно, приведем простейший пример из компьютерных игр.

Предположим, у нас есть компьютерная игра, в которую мы играли много-много раз. При этом ведется статистика: сыграно 100 игр, из них 30 побед, 70 поражений. Это и будет нашими входными данными. А решение будет таким: вероятность победы – 30%, проигрыша – 70%.

Можно использовать метод Монте-Карло для симуляции инвестиционного портфеля. Предположим, нам нужно получить доходность не менее 10%. Для этого подбираем инструменты с доходностью не меньше этой величины и вычисляем среднее арифметическое. Составляющие портфеля можно варьировать для получения максимальной доходности. Здесь входными данными будут наименование, стоимость и доходность отдельного инструмента, а искомым значением – общая доходность портфеля.

Процесс моделирования методом Монте-Карло

Имитационное моделирование методом Монте-Карло – это автоматизированный процесс, позволяющий рассматривать вероятность наступления различных событий. Каждая смоделированная ситуация является уникальной, что дает возможность оценить целый спектр рисков.

При создании модели все неопределенные факторы заменяются диапазоном возможных значений. К примеру, ни один аналитик, занимающийся оценкой рисков, не может знать, каким будет курс евро через 3-5 лет. Программа позволяет задать диапазон значений на усмотрение специалиста. Разумеется, здесь многое зависит от человека: требуется определенный уровень квалификации.

Далее система распределяет вероятности. Для оценки различных параметров применяются варианты распределения:

Нормальное распределение. Кривая нормального распределения или Гауссова кривая, выглядит так:

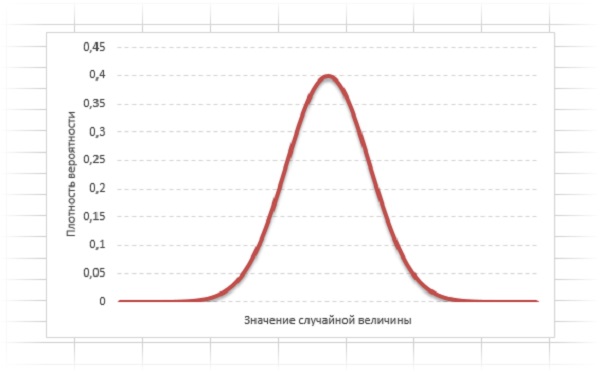
Значение случайной величины, расположенное посередине, характеризует наиболее высокую вероятность. Для построения кривой используются статистические данные: ожидаемое значение и стандартное отклонение. Такой вариант распределения подойдет, к примеру, для расчета стоимости коммунальных услуг в обозримом будущем.

Равномерное распределение. Все события могут наступить с одинаковой вероятностью, пользователю требуется лишь установить минимум и максимум.

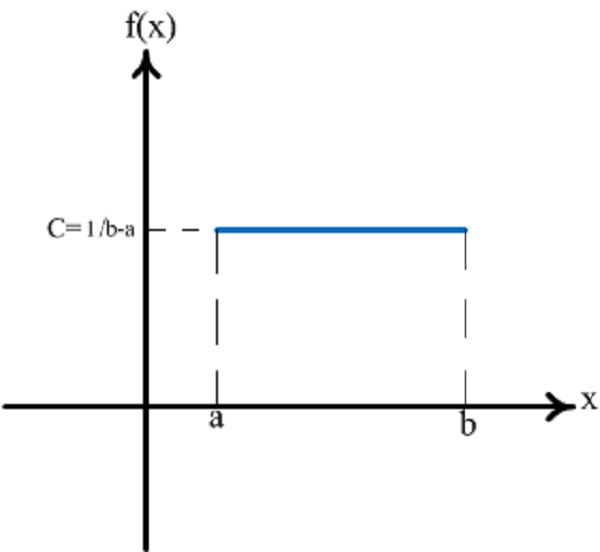
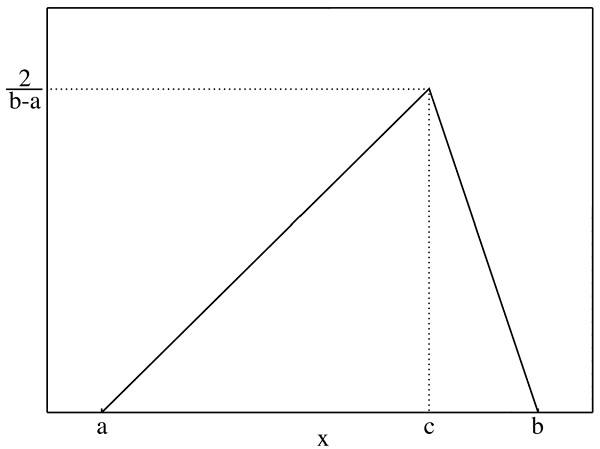
Кривая равномерного распределения имеет вид прямоугольника. На графике a и b – минимальные значения, С – вероятность. Подойдет для расчета условно-постоянных расходов в краткосрочном периоде.

Логнормальное распределение. Используется для расчета параметров, которые не могут принимать отрицательное значение, но могут расти до бесконечности. Пример: цены на энергоносители. График логнормального распределения выглядит несимметричным.

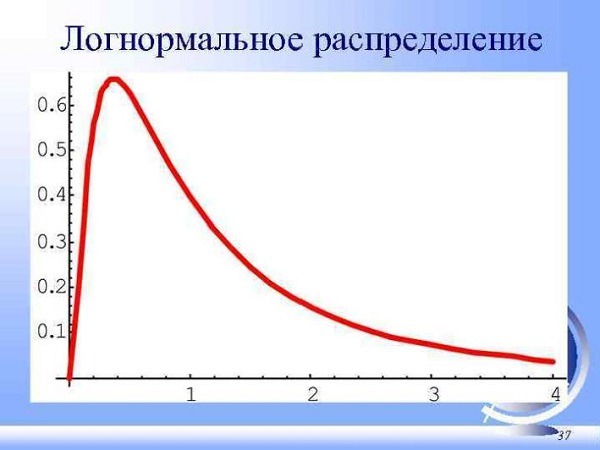
Дискретное распределение. Может применяться, к примеру, для компьютерных игр, где вычисляется процент побед и поражений. Пользователю требуется вычислить нужные значения из числа возможных.
Треугольное распределение. Определяются точки минимума, максимума и максимальной вероятности. Значения, близкие к точке максимальной вероятности, принимаются в качестве вероятных. Этот вариант применяется для анализа продаж, котировок ценных бумаг, прогноза финансовых результатов по итогам деятельности и др. Треугольное распределение подходит для имитационного моделирования рисков по методу Монте-Карло.

Итак, имитационное моделирование по методу Монте-Карло выполняется многократно. По результатам всех операций делается выборка значений, результаты систематизируются и определяется итоговая вероятность события.

Выходные данные

Выходными или итоговыми данными имитационного моделирования по методу Монте-Карло могут быть числовые значения или проценты. В отдельных случаях значения могут находиться внутри диапазона.

Однако итоги тестирования выражаются не только в цифрах. Возможно также выявление каких-то функций или параметров в модели, которые оказывают наибольшее влияние на результат. К примеру, наибольшее влияние на курс рубля оказывают цены на нефть на мировом рынке.

Сколько имитационных испытаний необходимо выполнить

Количество симуляций зависит от цели исследования. Как уже упоминалось, моделирование повторяется сотни, тысячи, иногда десятки тысяч раз – чем больше испытаний, тем более достоверный результат будет получен на выходе. При наличии программы не возникает проблем в многократном повторении операции.

Преимущества и недостатки метода

Достоинствами ММК являются:

Простота и универсальность – метод может применяться практически к любому типу данных.
ММК позволяет учитывать не только определенный тип данных в отдельности, но и взаимосвязи между различными типами данных.
Метод можно применять там, где не срабатывают привычные методы исследования, основанные на математических расчетах.

Иногда требуется проведение большого количества испытаний, что может занять много времени.
Для выполнения симуляций по методу Монте-Карло в программе необходимо привлекать квалифицированных специалистов.
Метод не может дать достоверную оценку для событий, характеризующихся очень низкой или очень высокой вероятностью наступления.

Примеры

Перейдем к практическим примерам использования метода Монте-Карло.

Пример 1. Рассмотрим ситуацию, когда 35-летний человек планирует уйти на пенсию в 60 лет.

планируемый ежемесячный размер пенсии – 75 000 руб. (1 000 $ или 29 000 грн.) ;
безопасная ставка снятия (SWR) – 4%;
ожидаемая доходность инвестиционного портфеля – 6%;
ожидаемая волатильность портфеля – 15%;
период для симуляции – 25 лет;
количество симуляций – 5000.

Таким образом, цель – накопить 300000$ (1000х12/0.04). Проверим вероятность этой суммы, используя симулятор. Программа выполнит 125000 симуляций (5000х25 лет).

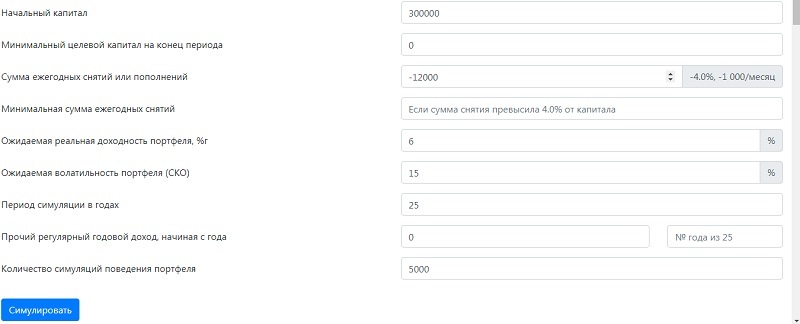
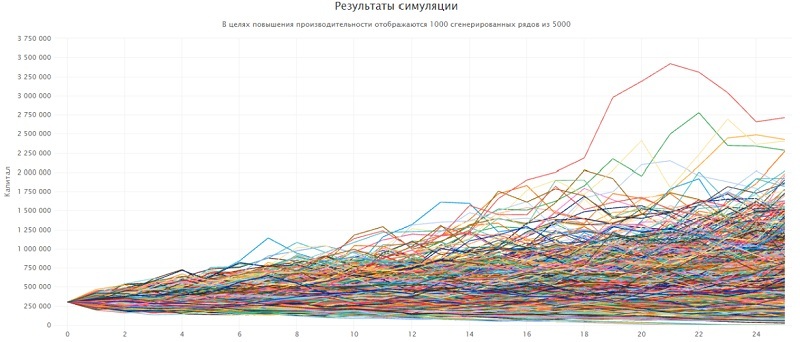
Итак, по первой строчке мы видим, что в 99,7% симуляций цель будет выполнена.

Пример 2. При тех же условиях зададим размер капитала, который мы планируем сохранить на конец периода. Для удобства примем эту сумму равной размеру начального капитала.

Здесь процент вероятности благоприятного развития событий уменьшился до 84,3%. Что с этим можно сделать?

В какие-то периоды, когда ситуация на рынке оставляет желать лучшего или не возникает крупных непредвиденных расходов, инвестор может снимать со счета меньшую сумму – не 900 000 руб. (12 000 $ или 348 000 грн.) в год, а, скажем, 525 000 руб. (7 000 $ или 203 000 грн.) – 600 000 руб. (8 000 $ или 232 000 грн.) . Кроме того, существует еще и государственная пенсия, которая индексируется на размер инфляционного процента.

Когда я смогу накопить

Метод Монте-Карло является примером подхода к моделированию на основе результатов анализа взаимосвязей между явлениями. В наших примерах эту взаимосвязь можно охарактеризовать так: доходность инвестиций → инфляция → волатильность портфеля → капитал.

начальный капитал – 1 500 000 руб. (20 000 $ или 580 000 грн.) ;
планируемая (ожидаемая) сумма ежегодных пополнений счета – 1 125 000 руб. (15 000 $ или 435 000 грн.) ;
размер прочего регулярного дохода – 900 000 руб. (12 000 $ или 348 000 грн.) в год;
период симуляции (максимальный срок для накопления капитала) – 20 лет.

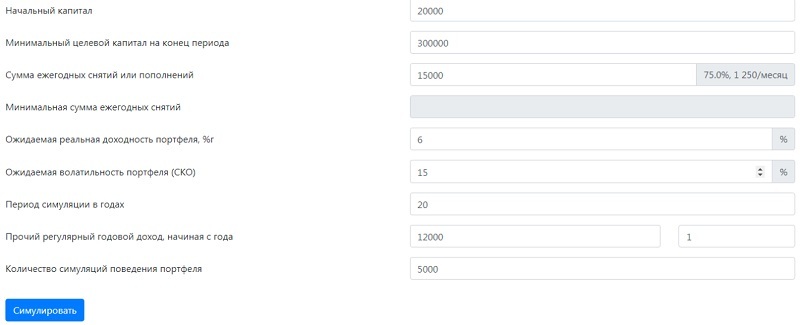
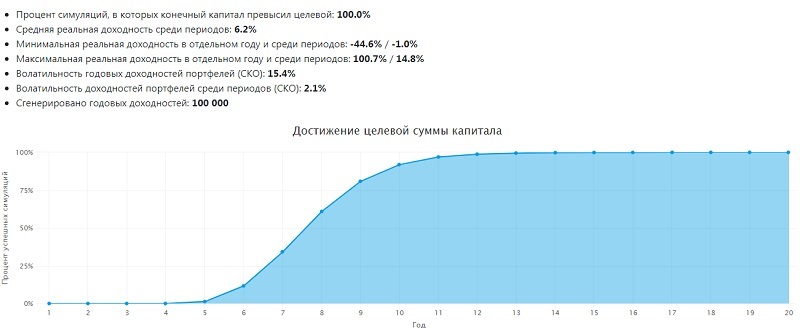
Из графика видно, что нужная сумма накопится примерно на 13-м году. Не следует забывать о падениях рынка, которые случаются раз в несколько лет. Вместе с тем, некоторые активы могут взлететь в цене, что принесет крупный незапланированный доход. Но ориентироваться лучше на срок с запасом в 2-3 года, т.е. примерно 15-16 лет с точки отсчета.

Заключение

Достаточно понять, что метод Монте-Карло основан на моделировании случайных процессов на основании заданных пользователем исходных данных. ММК успешно применяется там, где обычные математические расчеты могут дать недостоверные результаты.

Предусмотреть все случайности с вероятностью 100% сложно, поэтому метод допускает определенную погрешность, которая частично компенсируется количеством произведенных симуляций.

Анализ рисков с использованием метода моделирования Монте-Карло представляет собой сочетание методов анализа чувствительности и анализа сценариев. Это достаточно сложная методика, имеющая под собой, как правило, компьютерную реализацию. Результатом такого анализа выступает распределение вероятностей возможных результатов проекта. Имитационное моделирование по методу Монте-Карло позволяет построить математическую модель для проекта с неопределенными значениями параметров и, зная вероятностные распределения параметров проекта, а также связь между изменениями параметров (корреляцию), получить распределение доходности проекта.

При формировании сценариев с использованием методов имитационного моделирования применяется следующая последовательность действий:

• определяются интервалы возможного изменения исходных переменных, внутри которых эти переменные являются случайными величинами;

• определяются виды распределения вероятностей внутри заданных интервалов;

• устанавливаются коэффициенты корреляции между зависимыми переменными;

• многократно (не менее 200 раз) рассчитываются результирующие показатели;

• полученные результирующие показатели рассматриваются как случайные величины, которым соответствуют такие характеристики, как математическое ожидание, дисперсия, функция распределения и плотность вероятностей;

• определяется вероятность попадания результирующих показателей в тот или иной интервал, вероятность превышения минимально допустимого

Анализ значений результирующих показателей при сформированных сценариях позволяет оценить возможный интервал их изменения при различных условиях реализации проекта. Вероятностные характеристики используются для:

• принятия инвестиционных решений;

• обоснования рациональных размеров и форм резервирования и страхования.

На рис. 21.2.8 представлена схема работы с имитационной моделью.

Применение метода имитации Монте-Карло требует использования специальных математических пакетов (например, специализированного программного пакета Гарвардского университета под названием Risk-Master), в то время как метод сценариев может быть реализован даже при помощи обыкновенного калькулятора.

Рис. 21.2.8. Схема имитационного моделирования рисков проекта

Результатом такого комплексного анализа выступает распределение вероятностей возможных результатов проекта (например, вероятность получения чистого дисконтированного дохода ЧДД

Другая проблема, которая возникает как при использовании метода сценариев, так и при использовании метода Монте-Карло, состоит в том, что применение обоих методов не дает однозначного ответа на вопрос о том, следует ли все же реализовывать данный проект или отвергнуть его, поэтому, как правило, используется целый комплекс методов анализа рисков проекта для окончательной оценки.

Общая результативность анализа проектных рисков может быть оценена следующим образом.

Преимущества методов:

1) совершенствует уровень принятия решений по малоприбыльным проектам.

Проект с малым значением ЧДД может быть принят в случае, если анализ рисков установит, что шансы получить удовлетворительный доход превосходят вероятность неприемлемых убытков;

2) помогает идентифицировать производственные возможности.

Анализ рисков помогает сэкономить деньги, потраченные на поиск информации, издержки на получение которой превосходят издержки неопределенности;

3) освещает секторы проекта, требующие дальнейшего исследования, и

управляет сбором информации;

4) выявляет слабые места проекта и дает возможность внести поправки;

5) предполагает неопределенность и возможные отклонения факторов от базовых уровней. В связи с тем, что присвоение распределений и границ варьирования переменных несет оттенок субъективизма, необходимо критически подходить даже к результатам анализа рисков.

Сложности применения методов:

1) проблема коррелированных переменных, которые, если неправильно специфицированы, могут привести к неверным заключениям;

2) анализ рисков предполагает доброкачественность моделей проектного оценивания. Если модель неправильна, то результаты анализа рисков также будут вводить в заблуждение.

• определяются виды распределения вероятностей внутри заданных интервалов;

• устанавливаются коэффициенты корреляции между зависимыми переменными;

• многократно (не менее 200 раз) рассчитываются результирующие показатели;

• принятия инвестиционных решений;

• обоснования рациональных размеров и форм резервирования и страхования.

На рис. 21.2.8 представлена схема работы с имитационной моделью.

Рис. 21.2.8. Схема имитационного моделирования рисков проекта

Под метдом Монте-Карло понимается численный метод решения
математических задач при помощи моделирования случайных величин. Представление об истории метода и простейшие примеры его применения можно найти в Википедии.

В самом методе нет ничего сложного. Именно эта простота объясняет популярность данного метода.

Метод имеет две основных особенности. Первая — простая структура вычислительного алгоритма. Вторая — ошибка вычислений, как правило, пропорциональна
, где — некоторая постоянная, а — число испытаний. Ясно, что добиться высокой точности на таком пути невозможно. Поэтому обычно говорят, что метод Монте-Карло особенно эффективен при решении тех задач, в которых результат нужен с небольшой точностью.

Однако одну и ту же задачу можно решать различными вариантами метода Монте-Карло, которым отвечают различные значения . Во многих задачах удается значительно увеличить точность, выбрав способ расчета, которому соответствует значительно меньшее значение .

Общая схема метода

Допустим, что нам требуется вычислить какую-то неизвестную величину m. Попытаемся придумать такую случайную величину , чтобы . Пусть при этом .
Рассмотрим независимых случайных величин (реализаций), распределения которых совпадают с распределением . Если достаточно велико, то согласно центральной предельной теореме распределение суммы будет приблизительно нормальным с параметрами , .

На основе Центральной предельной теоремы (или если хотите предельной теоремы Муавра-Лапласа) не трудно получить соотношение:

где — функция распределения стандартного нормального распределения.

Это — чрезвычайно важное для метода Монте-Карло соотношение. Оно дает и метод расчета , и оценку погрешности.

В самом деле, найдем значений случайной величины . Из указанного соотношения видно, что среднее арифметическое этих значений будет приближенно равно . С вероятностью близкой к ошибка такого приближения не превосходит величины . Очевидно, эта ошибка стремится к нулю с ростом .

В зависимости от целей последнее соотношение используется по разному:

Точность вычислений

Как видно из приведенных выше соотношений, точность вычислений зависит от параметра и величины – среднеквадратичного отклонения случайной величины .

В этом пункте хотелось бы указать важность именно второго параметра . Лучше всего это показать на примере. Рассмотрим вычисление определенного интеграла.

Вычисление определенного интеграла эквивалентно вычислению площадей, что дает интуитивно понятный алгоритм вычисления интеграла (см. статью в Википедии). Я рассмотрю более эффективный метод (частный случай формулы для которого, впрочем, тоже есть в статье из Википедии). Однако не все знают, что вместо равномерно распределенной случайной величины в этом методе можно использовать практически любую случайную величину, заданную на том же интервале.

Итак, требуется вычислить определенный интеграл:

Выберем произвольную случайную величину с плотностью распределения , определенной на интервале . И рассмотрим случайную величину .

Математическое ожидание последней случайной величины равно:

Таким образом, получаем:

Последнее соотношение означает, что если выбрать значений , то при достаточно большом :

Таким образом, для вычисления интеграла, можно использовать практически любую случайную величину . Но дисперсия , а вместе с ней и оценка точности, зависит от того какую случайную величину взять для проведения расчетов.

Можно показать, что будет иметь минимальное значение, когда пропорционально |g(x)|. Выбрать такое значение в общем случае очень сложно (сложность эквивалентна сложности решаемой задачи), но руководствоваться этим соображением стоит, т.е. выбирать распределение вероятностей по форме схожее с модулем интегрируемой функции.

Численный пример

Теория, конечно, дело хорошее, но давайте рассмотрим численный пример: ; ; .

Вычислим значение интеграла с применением двух различных случайных величин.

В первом случае будем использовать равномерно распределенную случайную величину на [a,b], т.е. .

Во втором случае возьмем случайную величину с линейной плотностью на [a,b], т.е. .

Вот график, указанных функций

Нетрудно видеть, что линейная плотность лучше соответствует функции .

Точное значение интеграла легко вычислить аналитически, оно равно 1.

Результаты одного моделирования при :

Для равномерно распределенной случайной величины: .

Для случайной величины с линейной плотностью распределения: .

В первом случае относительная погрешность более 21%, а во втором 2.35%. Точность в первом случае равна 0.459, а во втором – 0.123.

Думаю, данный модельный пример показывает важность выбора случайной величины в методе Монте-Карло. Выбрав, правильную случайную величину, можно получить более высокую точность вычислений, при меньшем числе итераций.

Конечно, так не вычисляют одномерные интегралы, для этого есть более точные квадратурные формулы. Но ситуация меняется при переходе к многомерным интегралам, т.к. квадратурные формулы становятся громоздкими и сложными, а метод Монте-Карло применяется лишь с небольшими изменениями.

Количество итераций и генераторы случайных чисел

Не трудно видеть, что точность вычислений зависит от количества случайных величин включенных в сумму. Причем, для увеличения точности вычислений в 10 раз нужно увеличить в 100 раз.

При решении некоторых задач для получения приемлемой точности оценки требуется брать очень большое число . А учитывая, что метод зачастую работает очень быстро, то реализовать последнее при современных вычислительных возможностях совсем не сложно. И возникает соблазн просто увеличить число .

Если в качестве источника случайности используется некоторое физическое явление (физический датчик случайных чисел), то все работает отлично.

Часто для вычислений по методу Монте-Карло применяют датчики псевдослучайных чисел. Главная особенность таких генераторов – наличие некоторого периода.

Метод Монте-Карло можно использовать при значениях не превышающих (лучше много меньших) период вашего генератора псевдослучайных чисел. Последний факт вытекает из условия независимости случайных величин, используемых при моделировании.

При проведении больших расчетов нужно убедиться, что свойства генератора случайных чисел позволяют вам провести эти расчеты. В стандартных генераторах случайных чисел (в большинстве языков программирования) период чаще всего не превосходит 2 в степени разрядности операционной системы, а то и еще меньше. При использовании таких генераторов нужно быть чрезвычайно осторожным. Лучше изучить рекомендации Д.Кнута, и построить свой генератор, имеющий наперед известный и достаточно большой период.

Литература

Популярные лекции по математике 1968. Выпуск 46. Соболь И.М. Метод Монте-Карло. М.: Наука, 1968. — 64 с.

Читайте также: