Докажите основное тригонометрическое тождество 9 класс геометрия кратко

Обновлено: 02.07.2024

А вот выражение \(\frac=x\) является тождеством только при условии \(x≠0\) (иначе левая часть не существует).

Как доказывать тождество?

Рецепт до одури прост:

Для того, чтоб это сделать можно:

1. Преобразовывать только правую или только левую часть.
   
2. Преобразовывать обе части одновременно.
   
3. Использовать любые допустимые математические преобразования (например, приводить подобные; раскрывать скобки; переносить слагаемые из одной части в другую, меняя знак; умножать или делить левую и правую часть на одно и то же число или выражение, не равное нулю и т.д.).
   
4. Использовать любые математические формулы.
   

Именно четвертый пункт при доказательстве тождеств используется чаще всего, поэтому все формулы тригонометрии нужно знать, помнить и уметь использовать.

Пример. Доказать тригонометрическое тождество \(\sin⁡2x=2\sin⁡x\cdot \cos\)
Решение:

\(\sin⁡2x=2 \sin⁡x\cdot \cos \)

Будем преобразовывать левую часть.
Представим \(2x\) как \(x+x\)…

Левая часть равна правой – тождество доказано.

Пример. Доказать, что выражение \(\frac >>\) \(-\sin=1\) является тождеством.
Решение:

Будем преобразовывать только левую часть. Приведем слагаемые к общему знаменателю.

Применим в числителе вездесущие основное тригонометрическое тождество: \(\sin^2⁡+\cos^2=1\).

Левая часть равна правой, тождество доказано.

Пример. Доказать тригонометрическое тождество \(1-tg^2 t=\) \(\frac\)
Решение:

Здесь будем преобразовывать только правую часть, стремясь свести ее к левой. Левую же оставляем неизменной. Вспоминаем формулу двойного угла для косинуса .

Теперь сделаем почленное деление в дроби (т.е. применим правило для сложения дробей в обратную сторону): \(\frac\) \(=\) \(\frac\) \(+\) \(\frac\)

Первую дробь правой части сократим, а ко второй применим свойство степени : \(\frac\) \(=\) \((\frac)^n\) .

Ну, а синус деленный на косинус равен тангенсу того же угла:

Левая часть равна правой, тождество доказано.

Здесь будем преобразовывать обе части:
- в левой: преобразуем \(\cos⁡2t\) по формуле двойного угла;
- а в правой \(ctg(π+t)\) по формуле приведения .

Теперь работаем только с левой частью.
В числителе воспользуемся формулой сокращенного умножения , в знаменателе вынесем за скобку синус.

Сократим дробь на \(\cos+\sin\).

Почленно разделим дробь, превратив ее в две отдельные дроби.

Первая дробь это котангенс , а вторая равна единице.

Левая часть равна правой, тождество доказано.

Как видите, все довольно несложно, но надо знать все формулы и свойства.

Как доказать основное тригонометрическое тождество

Два простых способа вывести формулу \(\sin^2x+\cos^2x=1\). Нужно знать только теорему Пифагора и определение синуса и косинуса.

Ответы на часто задаваемые вопросы:

Там, где заканчиваются границы привычной и давно знакомой алгебры, начинаются владения тригонометрии. Давайте вооружимся всеми необходимыми формулами, чтобы в полном обмундировании преодолеть любые тригонометрические испытания.

О чем эта статья:

9 класс, 10 класс, ЕГЭ/ОГЭ

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Связь между sin и cos одного угла

Вы уже наверняка знаете, что тождественный — это равный.

Основные тригонометрические тождества — это равенства, которые устанавливают связь между синусом, косинусом, тангенсом и котангенсом одного угла. Это значит, что любую из этих функций можно найти, если известна другая функция.

Ключ к сердцу тригонометрии — основное тригонометрическое тождество. Запомните и полюбите его, чтобы отношения с тригонометрией сложились самым наилучшим образом:

sin 2 α + cos 2 α = 1

Из основного тождества вытекают равенства тангенса и котангенса, поэтому оно — ключевое.

Равенство tg 2 α + 1 = 1/cos 2 α и равенство 1 + сtg 2 α + 1 = 1/sin 2 α выводят из основного тождества, разделив обе части на sin 2 α и cos 2 α.

В результате деления получаем:

sin 2 α + cos 2 α = 1

Сумма квадратов синуса и косинуса одного угла тождественно равна единице.

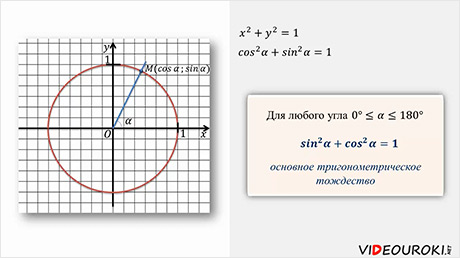
Чтобы доказать тождество, обратимся к теме единичной окружности.

Единичная окружность — это окружность с центром в начале прямоугольной декартовой системы координат. Радиус единичной окружности равен единице.

Докажем тождество sin 2 α + cos 2 α = 1

• Синус угла (sin α) — это отношение противолежащего катета к гипотенузе.
• Косинус угла (cos α) — это отношение прилежащего катета к гипотенузе.

Образовался прямоугольный треугольник OA₁B.

Основное тригонометрическое тождество связывает синус угла и косинус угла. Зная одно, вы легко можете найти другое. Нужно лишь извлечь квадратный корень по формулам:

Как видите, перед корнем может стоять и минус, и плюс. Основное тригонометрическое тождество не дает понять, положительным или отрицательным был исходный синус/косинус угла.

Как правило, в задачках с подобными формулами уже есть условия, которые помогают определиться со знаком. Обычно такое условие — указание на координатную четверть. Таким образом без труда можно определить, какой знак нам требуется.

Тангенс и котангенс через синус и косинус

• Синус угла — это ордината y.
• Косинус угла — это абсцисса x.
• Тангенс угла — это отношение ординаты к абсциссе.
• Котангенс угла — это отношение абсциссы к ординате.

Из всего этого множества красивых, но не сильно понятных слов, можно сделать вывод о зависимости одного от другого. Такая связь помогает отдельно преобразовывать нужные величины.

Исходя из определений:

Это позволяет сделать вывод, что тригонометрические тождества

задаются sin и cos углов.

Отсюда следует, что тангенс угла — это отношение синуса угла к косинусу. А котангенс угла — это отношение косинуса к синусу.

Отдельно стоит обратить внимание на то, что тригонометрические тождества

верны для всех углов α, значения которых вписываются в диапазон.

применимо для любого угла α, не равного π * z, где z — это любое целое число.

Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.

Связь между тангенсом и котангенсом

Уж насколько очевидной кажется связь между ранее рассмотренными тождествами, настолько еще более наглядна связь между тангенсом и котангенсом одного угла.

• Тождество записывается в следующем виде:
  tg α * ctg α = 1.

Такое тождество применимо и справедливо при любых углах α, значение которых не равняются π/2 * z, где z — это любое целое число. В противном случае, функции не будут определены.

Как и любое другое, данное тригонометрическое тождество подлежит доказательству. Доказывать его очень просто.

tg α * ctg α = 1.

Получается, что тангенс и котангенс одного угла, при котором они имеют смысл — это взаимно обратные числа.

Если числа a и b взаимно обратные — это значит, что число a — это число, обратное числу b, а число b — это число, обратное числу a. Кроме того, это значит, что числу a обратно число b, а числу b обратно число a. Короче, и так, и эдак.

Тангенс и косинус, котангенс и синус

Все тождества выше позволяют сделать вывод, что тангенс угла связан с косинусом угла, а котангенс угла — с синусом.

Эта связь становится очевидна, если взглянуть на тождества:

Сумма квадрата тангенса угла и единицы равна числу, обратному квадрату косинуса этого угла.

Сумма единицы и квадрата котангенса угла равна числу, обратному квадрату синуса этого угла.

Вывести оба этих тождества можно из основного тригонометрического тождества:
sin 2 α + cos 2 α = 1.

1. Для этого нужно поделить обе части тождества на cos 2 α, где косинус не равен нулю.
   
2. В результате деления получаем формулу tg 2 α + 1 =
   
3. Если обе части основного тригонометрического тождества sin 2 α + cos 2 α = 1 разделить на sin 2 α, где синус не равен нулю, то получим тождество:
   1 + ctg 2 α = .
   
4. Отсюда можно сделать вывод, что тригонометрическое тождество tg 2 α + 1 = применимо для любого угла α, не равного + π + z, где z — это любое целое число.
   
5. А тригонометрическое тождество 1 + ctg 2 α = применимо для любого угла, не равного π * z, где z — это любое целое число.

Хорошо бы выучить все формулы и запомнить формулировки тождеств наизусть. Чтобы это сделать, сохраняйте себе табличку с основными формулами.

Основные тригонометрические тождества

sin 2 α + cos 2 α = 1

tg 2 α + 1 =

1 + ctg 2 α =

Чтобы тратить еще меньше времени на решение задач, сохраняйте таблицу значений тригонометрических функции углов, которые чаще всего встречаются в задачах.

Примеры решения задач

Разберем пару задачек, для решения которых нужно знать основные тождества. Рассмотрите внимательно предложенные решения и потренируйтесь самостоятельно.

Задачка 1. Найдите cos α, tg α, ctg α при условии, что sin α = 12/13.

Чтобы решить задачу, необходимы следующие тригонометрические тождества:

Задачка 2. Найдите значение cos α,
если:

Чтобы решить задачу, необходимы следующие тригонометрические тождества:

Подставляем значения sin α:

Как видите, задачи решаются достаточно просто, нужно лишь верно применять формулы основных тождеств.

Основное тригонометрическое тождество связывает синус и косинус одного и того же угла. Сформулируем его: для любого угла справедливо:

Доказательство тождества

Рассмотрим тригонометрическую окружность (рис. 1). Выберем произвольный угол , тогда _>=OB" width="139" height="15" />
, а _>=AB" width="135" height="16" />
. В , как радиус единичной окружности. Так как треугольник прямоугольный, то для него можно записать теорему Пифагора:

Учитывая, что и , получаем

Что и требовалось доказать.

Следствие 1. Основное тригонометрическое тождество позволяет находить синус угла по известному косинусу или, наоборот, косинус угла по известному синусу. Справедливы формулы

Но для определения знака искомой тригонометрической функции требуется дополнительная информация о величине угла (например, в какой четверти расположен угол ).

Следствие 2. Из основного тригонометрического тождества можно вывести две формулы, связывающие соответственно косинус с тангенсом и синус с котангенсом.

1. Пусть +\pi n, \quad \left( n\in Z \right)" width="185" height="20" />
тогда . Разделим обе части основного тригонометрического тождества на ^>\alpha" width="45" height="16" />
:

после преобразования получим

:

после преобразования получим

Примеры решения задач

Задание	Найти значение , если и
Решение	По следствию 1 из основного тригонометрического тождества имеем

, получаем

Далее для определения знака косинуса, используем дополнительное условие, что . Значит, угол находится в первой четверти тригонометрического круга (рис. 2), а здесь . Таким образом, окончательно получим

Задание	Найти значение , если и
Решение	По следствию 1 из основного тригонометрического тождества, для нахождения синуса справедлива формула

, получим

Далее для определения знака искомого значения синуса, воспользуемся дополнительным условием о расположении угла: . Угол лежит во второй четверти тригонометрического круга (рис. 3), поэтому углу соответствуют только положительные значения синуса, поэтому окончательно:

Задание	Вычислить и , если и
Решение	По следствию 2, тангенс и косинус одного и того же угла связаны соотношением:

Выразим из него косинус:

, получим

По первому следствию из основного тригонометрического тождества

Для определения знаков синуса и косинуса, воспользуемся дополнительными условиями. Так как , следовательно, угол лежит в третьей четверти (рис. 4), там косинус и синус отрицательные. Тогда окончательно, получим

Задание	Вычислить и , если и
Решение	Сразу можно найти тангенс:

По следствию 2 из основного тригонометрического тождества, котангенс и синус связаны соотношением:

Выразим из него синус:

, получим

По первому следствию из основного тригонометрического тождества,

Для определения знаков синуса и косинуса, воспользуемся дополнительными условиями. Угол лежит в пределах , следовательно, он принадлежит четвертой четверти (рис. 5), там косинус положительный, а синус отрицательный. Окончательно, получим

Основное тригонометрическое тождество, так же используется при тождественных преобразованиях.

Задание	Вычислить
Решение	Сгруппируем первые два слагаемые заданного равенства и вынесем за скобки общий множитель :

полученное выражение в скобках есть основное тригонометрическое тождество и равно 1:

В этом видеофрагменте мы вспоминаем основное тригонометрическое тождество. Выводим формулы приведения и показываем, что с помощью формул приведения можно упростить вычисление синусов и косинусов углов.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.

Получите невероятные возможности

Конспект урока "Основное тригонометрическое тождество. Формулы приведения"

Прежде чем приступить к изучению нового материала, давайте вспомним, что для любого угла синусом угла называется ордината точки М,

а косинусом угла – абсцисса точки М.

Тангенсом угла называется .

Котангенсом угла называется .

Повторим таблицу значений синуса, косинуса, тангенса и котангенса для некоторых углов.

Еще вспомним уравнение окружности радиуса с центром в точке :

Уравнение окружности радиуса с центром в начале координат имеет вид:

Давайте изобразим единичную полуокружность.

Эта полуокружность – это часть окружности с центром в начале координат и радиусом, равным 1. Тогда уравнение этой окружности можно записать в виде

. То есть координаты всех точек должны удовлетворять этому уравнению.

Но координаты точки окружности есть не что иное, как косинус и синус угла, который соответствует этой точке. Тогда,
. Это равенство выполняется для любого угла . Мы доказывали подобное равенство для острых углов прямоугольного треугольника. Напомним, что это равенство называется основным тригонометрическим тождеством.

Задача. Лежат ли точки , , , , на единичной полуокружности?

Запишем уравнение, которое задает единичную окружность. Единичной полуокружности будут принадлежать те точки единичной окружности, для которых ордината изменяется от 0 до 1.

лежит на единичной полуокружности

не лежит на единичной полуокружности

лежит на единичной полуокружности

лежит на единичной полуокружности

не лежит на единичной полуокружности

Задача. Найти , если:

а) ;

б) .

а)

или

б)

или

Ответ: а) б) .

Задача. Найти , если:

а) ;

б) .

а)

или

б)

или

Ответ: а) б) .

Давайте вернемся к единичной полуокружности и проведем два луча ОМ и ОB.

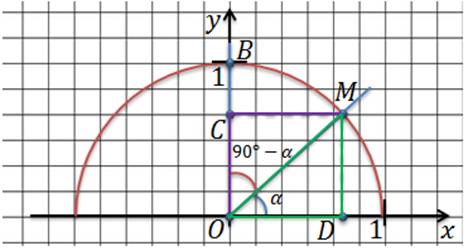
Из точки М проведем два перпендикуляра к осям и обозначим точки пересечения этих прямых с осями точками C и D. Очевидно,
.

Если угол DОМ= α, то . Рассмотрим треугольники DОМ и МОB. Это прямоугольные треугольники с общей гипотенузой ОМ.

Давайте посмотрим на полученные равенства. Итак, если , то

, .

Давайте проверим выполнение этих формул на конкретном примере.

Задача. Вычислить , .

Конечно, мы можем просто подставить табличные значения и все, но давайте попробуем решить эту задачу используя формулы, которые мы только что вывели.

Аналогично выводятся формулы , для всех углов α из промежутка от 0º до 180º. Вы можете вывести их самостоятельно. Эти формулы называются формулами приведения.

Задача. Вычислить , , , , , , , .

Подведем итоги урока. Сегодня на уроке мы вспомнили основное тригонометрическое тождество. И вывели формулы приведения. Эти формулы, как мы убедились на примерах, помогают упростить вычисления синусов, косинусов углов.

Тригонометрические тождества — это равенства, которые устанавливают связь между синусом, косинусом, тангенсом и котангенсом одного угла, которая позволяет находить любую из данных функций при условии, что будет известна какая-либо другая.

Основные тригонометрические тождества

\[ \sin^\alpha + \cos^ \alpha = 1 \]

\[ tg \alpha \cdot ctg \alpha = 1 \]

Четность, нечетность тригонометрических функций

\[ \sin \left ( - \alpha \right ) = - \sin \left ( \alpha \right ) \]

\[ \cos \left ( - \alpha \right ) = \cos \left ( \alpha \right ) \]

\[ tg \left ( - \alpha \right ) = - tg \left ( \alpha \right ) \]

\[ ctg \left ( - \alpha \right ) = ctg \left ( \alpha \right ) \]

Зависимость между синусом и косинусом

Данное тождество говорит о том, что сумма квадрата синуса одного угла и квадрата косинуса одного угла равна единице, что на практике дает возможность вычислить синус одного угла, когда известен его косинус и наоборот.

При преобразовании тригонометрических выражений очень часто используют данное тождество, которое позволяет заменять единицей сумму квадратов косинуса и синуса одного угла и также производить операцию замены в обратном порядке.

Нахождение тангенса и котангенса через синус и косинус

Данные тождества образуются из определений синуса, косинуса, тангенса и котангенса. Ведь если разобраться, то по определению ординатой \( \dfrac=\dfrac \) , а отношение \( \dfrac=\dfrac \) — будет являться котангенсом.

Добавим, что только для таких углов \( \alpha \) , при которых входящие в них тригонометрические функции имеют смысл, будут иметь место тождества \( tg \alpha = \dfrac \) , \( ctg \alpha=\dfrac \) .

Например: \( tg \alpha = \dfrac \) является справедливой для углов \( \alpha \) , которые отличны от \( \dfrac<\pi>+\pi z \) , а \( ctg \alpha=\dfrac \) — для угла \( \alpha \) , отличного от \( \pi z \) , \( z \) — является целым числом.

Зависимость между тангенсом и котангенсом

\[ tg \alpha \cdot ctg \alpha=1 \]

Данное тождество справедливо только для таких углов \( \alpha \) , которые отличны от \( \dfrac<\pi> z \) . Иначе или котангенс или тангенс не будут определены.

Опираясь на вышеизложенные пункты, получаем, что \( tg \alpha = \dfrac \) , а \( ctg \alpha=\dfrac \) . Отсюда следует, что \( tg \alpha \cdot ctg \alpha = \dfrac \cdot \dfrac=1 \) . Таким образом, тангенс и котангенс одного угла, при котором они имеют смысл, являются взаимно обратными числами.

Зависимости между тангенсом и косинусом, котангенсом и синусом

\( tg^ \alpha + 1=\dfrac <\cos^\alpha> \) — сумма квадрата тангенса угла \( \alpha \) и \( \alpha \) , отличных от \( \dfrac<\pi>+ \pi z \) .

\( 1+ctg^ \alpha=\dfrac<\sin^\alpha> \) — сумма \( \alpha \) , равняется обратному квадрату синуса данного угла. Данное тождество справедливо для любого \( \alpha \) , отличного от \( \pi z \) .

Формулы приведения

sin α + 2 π z = sin α , cos α + 2 π z = cos α t g α + 2 π z = t g α , c t g α + 2 π z = c t g α sin - α + 2 π z = - sin α , cos - α + 2 π z = cos α t g - α + 2 π z = - t g α , c t g - α + 2 π z = - c t g α sin π 2 + α + 2 π z = cos α , cos π 2 + α + 2 π z = - sin α t g π 2 + α + 2 π z = - c t g α , c t g π 2 + α + 2 π z = - t g α sin π 2 - α + 2 π z = cos α , cos π 2 - α + 2 π z = sin α t g π 2 - α + 2 π z = c t g α , c t g π 2 - α + 2 π z = t g α sin π + α + 2 π z = - sin α , cos π + α + 2 π z = - cos α t g π + α + 2 π z = t g α , c t g π + α + 2 π z = c t g α sin π - α + 2 π z = sin α , cos π - α + 2 π z = - cos α t g π - α + 2 π z = - t g α , c t g π - α + 2 π z = - c t g α sin 3 π 2 + α + 2 π z = - cos α , cos 3 π 2 + α + 2 π z = sin α t g 3 π 2 + α + 2 π z = - c t g α , c t g 3 π 2 + α + 2 π z = - t g α sin 3 π 2 - α + 2 π z = - cos α , cos 3 π 2 - α + 2 π z = - sin α t g 3 π 2 - α + 2 π z = c t g α , c t g 3 π 2 - α + 2 π z = t g α

Формулы понижения степени

sin 2 α = 1 - cos 2 α 2 cos 2 α = 1 + cos 2 α 2 sin 3 α = 3 sin α - sin 3 α 4 cos 3 α = 3 cos α + cos 3 α 4 sin 4 α = 3 - 4 cos 2 α + cos 4 α 8 cos 4 α = 3 + 4 cos 2 α + cos 4 α 8

Читайте также:

  
• Аппликация на тему посуда в старшей группе в детском саду
  
• Методика тоцкого для начальной школы
  
• Отчет по медосмотрам в школе
  
• Приказ о проведении акции по пдд в доу
  
• Маркетинговое исследование школы примеры готовые