Дифференцирование функции это кратко

Обновлено: 07.07.2024

Дифференцирование – это определение производной.

Если с - постоянное число, и u = u(x), v = v(x) - некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования:

5) если y = f(u), u=φ(x), т.е. y = f(φ(x)) - сложная функция (суперпозиция) которая составлена из дифференцируемых функций φ и f, то , или

6) если для функции y = f(x) существует обратная дифференцируемая функция x = g(y), при этом больше или меньше нуля, то .

На основе определения производной и правил дифференцирования можно составить список табличных производных основных элементарных функций:

Если вам нужно решить задачу, в рамках которой требуется вычислить производную какой-либо функции с одной переменной, советуем внимательно прочесть эту статью. Здесь приводятся общие положения теории дифференцирования, имеющие отношение к вычислению производной. Для этого могут быть использованы разные способы, ведь исходная функция может быть задана явно или неявно, в параметрическом виде, быть элементарной, основной или сложной, значит, в каждой ситуации бывает нужен свой подход.

Таблица дифференцирования функции

Мы собрали всю информацию, которую нужно знать для правильного дифференцирования функции, и представили ее в табличном виде:

Степенная фунция y = x p

x p ' = p · x p - 1

y = a x a x ' = a x · ln a

В частности, при a = e имеем

y = e x e x ' = e x

С · f ( x ) ' = C · f ' ( x ) , C ∈ R ( f ( x ) ± g ( x ) ' = f ' ( x ) ± g ' ( x ) ( f ( x ) g ( x ) ) ' = f ' ( x ) g ( x ) + f ( x ) g ' ( x ) f ( x ) g ( x ) ' = f ' ( x ) · g ( x ) - f ( x ) · g ' ( x ) g 2 ( x )

log a x ' = 1 x · ln a

В частности, при a = e имеем

y = ln x ln x ' = 1 x

sin x ' = cos x cos x ' = - sin x t g x ' = 1 cos 2 x c t g x ' = - 1 sin 2 x

Производная сложной функции

( f ( g ( x ) ) ) ' = f ' ( g ( x ) ) · g ' ( x )

Производная неявно заданной функции

F ( x , y ) = 0 ⇒ y ' x = - F ' x ( x , y ) F ' y ( x , y )

Производная обратной функции

g ' y ( y ) = 1 f ' x ( x ) , f ' x ( x ) = 1 g ' y ( y )

Обратные тригонометрические функции

a r c sin x ' = 1 1 - x 2 a r c cos x ' = - 1 1 - x 2 a r c t g x ' = 1 1 + x 2 a r c c t g x ' = - 1 1 + x 2

s h x ' = c h x ( c h x ) ' = s h x ( t h x ) ' = 1 c h 2 x ( c t h x ) ' = - 1 s h 2 x

Производная параметрически заданной функции

x = φ ( t ) , y = ψ ( t ) , t ∈ ( a ; b ) y x ' = ψ ' ( t ) φ ' ( t ) y x '' = ψ '' ( t ) · φ ' ( t ) - ψ ' ( t ) · φ '' ( t ) φ ' ( t ) 3

y = f ( x ) y ' = y · ( ln ( f ( x ) ) ) '

Пояснения таблицы

Содержимое таблицы требует небольших пояснений. Например, в наиболее простом случае для дифференцирования нам пригодится определение производной, т.е. вычисление соответствующего предела. Это действие носит название непосредственного дифференцирования.

Если вам приходится работать с основной элементарной функцией, то следует использовать таблицу основных производных. В ней приводятся все готовые значения, доказанные на основании определения. Это очень удобно, и мы советуем вам держать такую таблицу под рукой.

Если надо вычислить производную суммы функций или их разности, произведения и дробного выражения с функцией, то нужно воспользоваться правилами дифференцирования. Они пригодятся при решении большинства задач. Таблица производных, основные правила дифференцирования и формула нахождения производной сложной функции позволят вам выполнить дифференцирование любой элементарной функции при условии, что она задана в явном виде y = f ( x ) .

В случае, когда нужно найти производную показательно степенной функции y = ( f ( x ) ) g ( x ) , удобно пользоваться формулой логарифмической производной. Также она полезна при нахождении производных тогда, когда исходное выражение представляет из себя большую и громоздкую дробь.

Работу с функциями, заданными параметрически, т.е. в виде x = φ ( t ) , y = ψ ( t ) , t ∈ a ; b , мы подробно разобрали в отдельной статье.

Если функция задана неявно в виде F ( x ; y ) = 0 , то тут возможны несколько методов нахождения производной. Можно провести вычисления, основываясь на понятии частных производных. Еще один вариант – вычислить производные обеих частей равенства, приняв y как функцию от x, после чего разрешить полученное уравнение относительно производной.

В основном эта операция применяется для исследования функций, а также величин, изменяющихся с течением времени.

В этом случае необходимо знать правила дифференцирования. Это довольно простая задача, когда функция соответствует табличному значению.

Однако бывают случаи, когда она является сложной.

Общая информация

Нахождение производной (дифференцирование) функции является одной из важнейших математических операций. Это позволяет существенно сократить объем вычислений. Например, при исследовании какой-либо функции, необходимо найти ее область значения. Существует множество методов решения данной задачи, но только нахождение производной позволяет оптимизировать вычисления. В данном случае к оптимизации относится экономия времени и сокращение объемов вычислений.

Дифференцирование применяется не только в математике, но и в некоторых других сферах человеческой жизни. Это прежде всего объясняется количеством затраченного времени и простотой расчетов.

Сферы использования

В физике с ее помощью можно найти такие величины: силу, ускорение, мощность, массу тонкого физического тела (стержня), скорость, теплоемкость, мгновенные значения тока и напряжения, а также другие величины. Последние должны изменяться с течением времени или по какому-либо закону. Если величина является постоянной (константой), то ее производная равна 0.

В химии и фармацевтике операция дифференцирования получила также широкое применение. Ее следует применять для точного расчета массы или массовой доли реактивов. Кроме того, она позволяет найти оптимальную дозу лекарственного препарата, при которой эффект будет максимальным, а побочные действия — минимальными.

Агропромышленный комплекс тоже нуждается в выполнении данной операции. Например, для определения оптимальности соотношения сторон земельных участков. В современных экономических исследованиях применяются определенные математические функции. Для их исследования необходимы знания в области дифференцирования.

Для анализа нужно применять алгоритм, позволяющий существенно уменьшить затраченное время. Для этих целей специалисты рекомендуют применять дифференцирование.

Понятие производной

Производная некоторой функции является дифференциальным исчислением, которое характеризует ее скоростное изменение в искомой точке. Более сложное определение: предел отношения приращения функции к приращению ее аргумента с тем условием, что последнее стремится к 0. Главное условие — предел должен существовать. Если его нет, то функция не меняется и является константой. В этом случае говорят, что производной не существует, поскольку она равна 0.

Функция, которая имеет производную в определенной точке, называют дифференцируемой в этой точке. Процесс нахождения производной является дифференцированием. Обратная операция по нахождению первообразной — интегрированием. Она имеет два смысла: геометрический и физический.

К первому следует отнести тангенс угла наклона касательной прямой к некоторому графику. Сначала выбирается секущая (прямая, пересекающая график в двух и более точках). После этого нужно взять любую точку, полученную при пересечении. Затем, используя точку в качестве оси вращения, изменить плавно положение секущей. В некоторый момент она окажется касательной, т. е. будет иметь только одну точку соприкосновения с графиком.

Физический смысл — скорость изменения функции. Нужно рассмотреть закон движения S = s(t). Выражение является законом, который описывает прямолинейное движение физического тела. Нужно найти мгновенную скорость (V) в момент времени to: V(to) = [s(to)]'. Если взять еще одну производную, то получится величина, называемая ускорением: a(to) = [V(to)]' = [s(to)]''.

Табличные значения

Для нахождения дифференциала какой-либо функции необходимо выполнить некоторые вычисления, которые могут занять время. Специалисты позаботились об экономии времени. Они составили таблицу элементарных функций (рис. 1).

Их и следует применять для решения задач. Если задача является довольно простой, то правила нахождения производной сводятся к элементарным операциям.

Для этого достаточно применить простой алгоритм для чайников:

Выполнить преобразование или упрощение выражения до табличного значения.
Взять производную и записать результат.

Во втором пункте следует руководствоваться табличными значениями. Например, следует продифференцировать степенную функцию вида y = x^3 / 3. Для решения задания необходимо выполнить преобразование — вынести константу: y = (2/3) * x^3. По таблице на рисунке 1 можно найти дифференциал: y' = (2/3) * (x^3)' = (2/3) * 3 * x^2 = 2x^2.

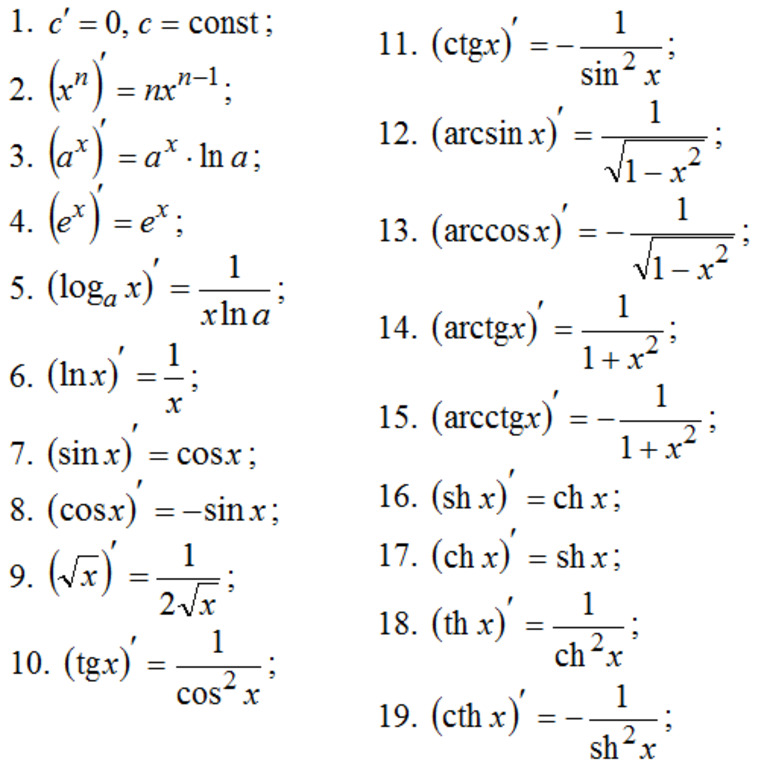
Рисунок 1. Производные простых функций.

Однако не все задачи являются простыми, поскольку существуют сложные функции, для которых необходимо применять правила дифференцирования сложной функции. Кроме того, нужно разобрать основные правила дифференцирования. Их можно применять и для простых выражений.

Правила дифференцирования

Для выполнения операции нахождения производной существуют определенные правила, которые позволяют правильно произвести взятие дифференциала некоторой функции.

Правила — порядок действий, позволяющих исключить неверные решения задач. Они получены в результате доказательств теорем и следствий из них. Первые необходимы для доказательства некоторых утверждений, которые могут заметно облегчить вычисления.

Простым примером является нахождение гипотенузы прямоугольного треугольника (длины катетов известны). Следует воспользоваться теоремой Пифагора. Нет необходимости доказывать, что квадрат гипотенузы равен сумме квадратов катетов, поскольку это забирает время. Существуют такие свойства (правила) дифференциации:

Вынесение константы за знак дифференциала: (C * f(x))' = C(f(x))'.
Если функция представлена в виде суммы (разности) двух функций, то при ее дифференцировании нужно найти производные каждого элемента: (y(x) + z(x))' = y'(x) + z'(x) и (y(x) - z(x))' = y'(x) - z'(x).
Дифференциал умножения функций f(x) и g(x) равен сумме произведений каждой функции на производную другой: (y(x) * z(x))' = (y'(x) * z(x) + y(x) * z'(x).
Производная частного функций y(x) и z(x) равна числителю, который представляет собой разность произведений знаменателя на дифференциал числителя, и производной знаменателя, умноженного на числитель. Кроме того, знаменатель — квадрат знаменателя исходной дроби: (y(x) / z(x))' = [(y'(x) * z(x) - y(x) * z'(x)] / (z(x))^2.

Каждое из правил необходимо применять в конкретной ситуации. Например, если нужно выполнить нахождение дифференциала суммы двух функций, умноженных на константу, то можно воспользоваться двумя правилами.

Алгоритм для сложной функции

Нахождение производной существенно усложняется в том случае, когда функция является сложной. Она состоит из нескольких элементарных выражений. Необходимо находить дифференциал каждой отдельно. Для этой цели пригодятся свойства нахождения производной, каждое из которых следует применять в конкретной ситуации.

Специалисты рекомендуют новичкам воспользоваться некоторым алгоритмом. Он позволяет существенно сократить время и количество вычислений. Решать без алгоритма не рекомендуется, поскольку это можно сделать неверно. Кроме того, необходимо воспользоваться формулами дифференцирования — таблицей производных для их отыскания.

Для сложной функции вида y(g(f(x))) порядок ее дифференцирования следующий:

Разбить функцию на составные части.
Найти производную f(x) и записать ее вначале.
Выполнить дифференцирование g, а затем записать ее после f(x): f'(x) * g'(f(x)).
Взять производную y, после этого умножить ее на результат, полученный в пункте 2: f'(x) * g'(f(x)) * y'(g(f(x))).

Принцип очень прост — следует начинать вычислять производную справа налево по частям.

Например, следует найти дифференциал функции y = (1/2) * sin (2x^2 - 6x).

Для наглядности нужно воспользоваться специальным алгоритмом:

Функция имеет вид y = f(g(x)), и состоит из двух частей: g(x) = 2x^2 - 6x и f(x) = sin(g(x)).
Производная первого элемента: g'(x) = (2x^2 - 6x)' = 4x - 6.
Дифференциал 2 функции: f'(x) = [sin(g(x))]' = cos(g(x)).
Получение результата (можно также упростить выражение при необходимости): y' = [(1/2) * sin (2x^2 - 6x)]' = (1/2) * [sin (2x^2 - 6x)]' = (1/2) * (4x - 6) * cos(2x^2 - 6x) = (2x - 3) * cos(2x^2 - 6x).

При решении задачи было задействовано свойство выноса константы за знак дифференциала. Кроме того, функция g(x) — разность двух выражений, производная которых находится по второму свойству дифференцирования. Функция может содержать в своем составе много элементов, но принцип только один.

Следует обратить внимание на первый пункт алгоритма, поскольку нужно правильно разбивать функцию на элементы. На начальной стадии обучения математики рекомендуют воспользоваться онлайн-калькулятором. Он позволяет получить правильное решение. Его можно сравнить результатом, который получен при решении ручным методом.

Пример решения

Сложность задачи зависит от самой функции. Например, если она является простой, то найти ее дифференциал не составит особой сложности. Для этого необходимо просто воспользоваться таблицей производных. В некоторых случаях следует воспользоваться некоторыми свойствами.

Например, необходимо найти дифференциал функции y = 8 * [(3x^3) + ln(x)] / (x^2). Для решения нужно воспользоваться следующими правилами: вынос константы, поиск производной суммы и частного. Найти дифференциал можно таким образом: y' = [8 * [(3x^3) + ln(x)] / (x^2)]' = 8 * [((3x^3 + ln(x))' * x^2 - (3x^3 + ln(x)) * (x^2)') / (x^2)^2] = 8 * [(x^2 + 1/x) * x^2 - 2x * (3x^3 + ln(x))] / x^4 = 8 * [(x^2(x - 6) + 1 - 2ln(x)) / x^3.

Специалисты не рекомендуют находить производные с помощью специализированного программного обеспечения. Бывают случаи, когда в поле для обработки выражение вводится неверно. При этом дифференциал является ошибочным. Кроме того, иногда бывают программные сбои, которые влекут за собой получение ложного результата. В любом случае нужно уметь дифференцировать функции любой сложности.

Таким образом, для нахождения дифференциала произвольной функции следует знать таблицу производных, основные правила и алгоритмы ее нахождения. Рекомендует проверять результат, полученный при вычислении, при помощи онлайн-калькулятора производных.

Определение дифференцируемой функции одной переменной в точке. Важность понятия дифференцируемости для функций, зависящих от многих переменных. Доказательство теорем: об эквивалентности дифференцируемости и существованием производной; о непрерывности дифференцируемой функции.

Определение дифференцируемой функции

Дифференцируемая функция в точке Пусть функция f ( x ) определена в некоторой окрестности точки .
Функция называется дифференцируемой в точке , если ее приращение в этой точке можно представить в виде суммы линейной функции от и о-малого по сравнению с :
(1) .
Здесь A – действительное число, ;
– о-малое по сравнению с при . То есть
, где .

Число A в определении (1) не зависит от , но оно зависит от точки , в которой вычисляется приращение. То есть A является функцией от (но не от ). Поэтому вместо (1) можно записать так:
.
Или, заменив на x , так:
.

Как мы увидим ниже, определение дифференцируемой функции одной переменной эквивалентно существованию ее производной. Тогда возникает вопрос – почему нельзя сразу дать определение, что дифференцируемая функция – это функция, имеющая производную?

Ответ на этот вопрос раскрывается при рассмотрении функций нескольких переменных. Дело в том, что производные вычисляются только от функций, зависящих от одной переменной. Для функций двух и более переменных, вначале выбирают направление приближения к заданной точке (например, ось x или ось y ), а затем по этому направлению вычисляют производную. Поэтому в любой точке имеется бесконечное множество производных по различным направлением. Из-за этого производные не фигурируют в определении дифференцируемой функции.

По сути, мы хотим ввести новый класс функций, с которыми проще работать методами бесконечно малых величин. Самыми простыми являются линейные функции. Поэтому желательно выделить такой класс функций, приращения которых можно свести к линейным операциям. Это можно сделать, если потребовать, чтобы приращение функции было линейной функцией от приращений ее аргументов плюс о-малое по сравнению с этими приращениями. Такие функции называются дифференцируемыми. Например, для функции двух переменных можно записать так:
,
где – действительные числа не зависящие от ;
– норма вектора .

Дифференцируемая функция многих переменных в точке Пусть функция определена в некоторой окрестности точки , .
Функция f называется дифференцируемой в точке , если ее приращение в этой точке можно представить в виде суммы линейной функции от приращений ее аргументов и о-малого по сравнению с нормой приращений аргументов:
.
Здесь – действительные числа, ;
– о-малое по сравнению с при ;
.

Свойства дифференцируемой функции

Теорема
Функция дифференцируема в точке тогда и только тогда, когда в этой точке существует производная . При этом
.
Доказательство ⇓

Таким образом, в случае функции от одной переменной, дифференцируемость функции в точке эквивалентно существованию производной в этой точке. Забегая вперед укажем, что в случае функций многих переменных, для того чтобы функция была дифференцируемой в точке, необходимо, чтобы она имела в этой точке частные производные, и достаточно, чтобы она имела в этой точке непрерывные частные производные.

Теорема
Пусть функция дифференцируема в точке . Тогда она непрерывна в этой точке.
Доказательство ⇓

Заметим, что обратное неверно. Если функция непрерывна в точке, то она может не быть дифференцируемой в этой точке. Так функция непрерывна для всех x , но не имеет производной при . См пример

Доказательства теорем

Связь дифференцируемости функции с существованием производной

Все свойства ⇑ Теорема
Функция дифференцируема в точке тогда и только тогда, когда в этой точке существует производная . При этом
.

1) Пусть функция дифференцируема в точке , то есть выполняется (1):
.
Разделим на и выполним переход :
;
.
Здесь, согласно свойству о-малого, . Отсюда получаем, что существует конечный предел
,
который является производной функции в точке : .

2) Пусть в точке существует производная . Это означает, что существует предел:
.
Воспользуемся свойством бесконечно малых функций. согласно которому, для существования предела необходимо и достаточно, чтобы функция имела вид , где – бесконечно малая функция при .

В нашем случае это означает, что
.
Отсюда
.

Связь дифференцируемости функции с ее непрерывностью

Все свойства ⇑ Теорема
Пусть функция дифференцируема в точке . Тогда она непрерывна в этой точке.

Используем определение непрерывности функции в точке. Согласно этому определению, функция f непрерывна в , если
1) определена в некоторой окрестности ;
2) существует предел при , и он равен :
.

Пусть функция дифференцируема в точке . Тогда согласно определению ⇑, она определена в некоторой окрестности точки . Пункт 1) выполнен.

Докажем, что выполняется пункт 2) . Поскольку дифференцируема в точке , то выполняется (1):
.
Выполняем предельный переход :
;
;
;
.
Сделаем подстановку . Тогда при . Последнее уравнение принимает вид:
.

Использованная литература:
О.И. Бесов. Лекции по математическому анализу. Часть 1. Москва, 2004.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.

Читайте также: