Дифференциал функции одной переменной кратко

Обновлено: 04.07.2024

Рассмотрим функцию , которая определена и непрерывна в точке и некоторой ее окрестности и дифференцируема в точке .

Функция дифференцируема, следовательно, существует ее производная

По теореме 1 § 11 имеем:

где – б/м функция при , следовательно,

где – б/м функция при ( ), большего порядка малости, чем . Таким образом, получили:

следовательно, функция сильнее стремится к нулю. Основной вклад в разложение (1) делает первое слагаемое.

– главная часть разложения приращения функции по .

Пусть приращение функции представимо в виде:

где – б/м функция при ( ), большего порядка малости, чем . Покажем, что функция в этом случае дифференцируема. Действительно:

(т.к. стремится к нулю быстрее, чем ), следовательно, существует производная

Если функция представима в виде (2), то говорят, что функция дифференцируема.

Определение.Дифференциалом функции называется величина, пропорциональная бесконечно малому приращению аргумента и отличающаяся от соответствующего приращения функции на бесконечно малую величину более высокого порядка чем .

Дифференциал функции обозначается через или .

Необходимым и достаточным условием существования дифференциала функции в точке служит существование ее производной в этой точке, и тогда

Определение.Приращение независимой переменой называют ее дифференциалом , т.е.

Дифференциал функции равен ее производной, умноженной на дифференциал независимой переменной, т.е.

Рассмотрим геометрическую иллюстрацию дифференциала функции (рис. 21). Т.к. , то дифференциал измеряет отрезок .

Дифференциал функции в точке численно равен приращению ординаты касательной, построенной к графику функции в точке , соответствующему изменению аргумента от значения до значения .

Приращение функции изображается приращением ординаты точки линии (отрезок ). Поэтому разность между дифференциалом и приращением изображается отрезком , заключенным между линией и касательной к ней; длина этого отрезка является при бесконечно малой величиной более высокого порядка, чем длина отрезка .

2 0 . Свойства дифференциала функции

3 0 . Дифференциал сложной функции. Свойство инвариантности

Рассмотрим свойство дифференциала функции, вытекающее из правила дифференциала сложной функции.

Пусть и – непрерывные функции своих аргументов, имеющие производные по этим аргументам и . Если обозначить , то . Умножая обе части уравнения на , получим:

т.е. дифференциал имеет такой же вид, как если бы величина была бы независимой переменной.

Дифференциал функции сохраняет одно и то же выражение, независимо от того, является ли ее аргумент независимой переменной или функцией от независимой переменной.

Это свойство называется инвариантностью (т.е. неизменностью) формы дифференциала.

4 0 . Приближенное вычисление с помощью дифференциала

Пусть в точке производная функции отлична от нуля: . Тогда

где – б/м величина при более высокого порядка, чем .Но при указанном условии она будет б/м величиной более высокого порядка и чем и . Действительно, при имеем:

ибо , а . Значит, и отличаются друг от друга на бесконечно малую величину более высокого порядка, чем они сами, и, следовательно, они эквивалентны:

Отсюда получаем приближенную формулу вычисления:

Формула (3) называется формулой приближенного вычисления с помощью дифференциала.

Пример 1. Вычислить приближенно .

Решение. Имеем: , , . Тогда:

Пример 2. Вычислить приближенно .

Решение. Имеем: , , . Тогда:

5 0 . Дифференциалы высших порядков

Пусть дана дифференцируемая функция . Тогда .

Определение. Дифференциалом второго порядка функции называется дифференциал от функции : .

Дифференциалом -го порядка называется дифференциал от дифференциала -го порядка как функции : .

Найдем выражение второго дифференциала функции . Т.к. не зависит от , то при дифференцировании считаем постоянным:

Отсюда находим, что .

1 0 . Дифференциал и его геометрический смысл

Функция дифференцируема, следовательно, существует ее производная

По теореме 1 § 11 имеем:

где – б/м функция при , следовательно,

где – б/м функция при ( ), большего порядка малости, чем . Таким образом, получили:

следовательно, функция сильнее стремится к нулю. Основной вклад в разложение (1) делает первое слагаемое.

– главная часть разложения приращения функции по .

Пусть приращение функции представимо в виде:

(т.к. стремится к нулю быстрее, чем ), следовательно, существует производная

Если функция представима в виде (2), то говорят, что функция дифференцируема.

Дифференциал функции обозначается через или .

Определение.Приращение независимой переменой называют ее дифференциалом , т.е.

Дифференциал функции равен ее производной, умноженной на дифференциал независимой переменной, т.е.

2 0 . Свойства дифференциала функции

3 0 . Дифференциал сложной функции. Свойство инвариантности

Рассмотрим свойство дифференциала функции, вытекающее из правила дифференциала сложной функции.

т.е. дифференциал имеет такой же вид, как если бы величина была бы независимой переменной.

Это свойство называется инвариантностью (т.е. неизменностью) формы дифференциала.

4 0 . Приближенное вычисление с помощью дифференциала

Пусть в точке производная функции отлична от нуля: . Тогда

Отсюда получаем приближенную формулу вычисления:

Формула (3) называется формулой приближенного вычисления с помощью дифференциала.

Пример 1. Вычислить приближенно .

Решение. Имеем: , , . Тогда:

Пример 2. Вычислить приближенно .

Решение. Имеем: , , . Тогда:

5 0 . Дифференциалы высших порядков

Пусть дана дифференцируемая функция . Тогда .

Определение. Дифференциалом второго порядка функции называется дифференциал от функции : .

Дифференциалом -го порядка называется дифференциал от дифференциала -го порядка как функции : .

При выполнении некоторых расчётов в исследованиях, проектировании, анализе полученных опытных путём данных часто возникает необходимость предварительной прикидки результата, которую удобно выполнять, используя дифференциал функции. Приближённые вычисления, выполненные с его помощью, могут дать новые направления дальнейшего изучения объектов и их разработок.

Понятие и геометрический смысл дифференциала

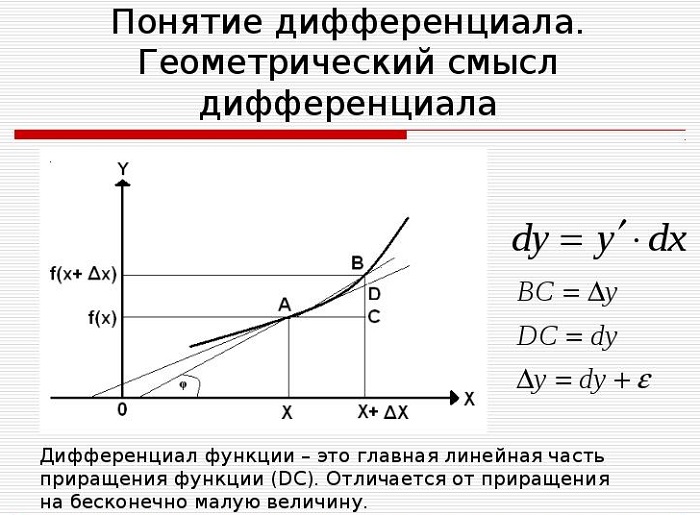
Пусть y = f (x) имеет производную

Применяя свойства предела функции, получают равенство

После умножения обеих частей на приращение аргумента Δx, образуется тождество:

в котором в правой части записано слагаемое, являющееся бесконечно малой одного порядка с Δx, далее идет слагаемое более высокого порядка.

Определение 1

Дифференциалом функции y = f (x) первого порядка называется главная часть её приращения f′(x)Δx, которую обозначают dy (или d(f(x)).

Для наглядного представления и понимания определения рассматривается касательная к графику функции y = f(x) в точке x. Когда значение переменной сдвигается по построенной прямой (получает приращение) на некоторую малую величину Δx, значение второй координаты точки тоже меняется.

Значит, дифференциал функции y = f(x) в точке x равен приращению ординаты касательной, когда её абсцисса меняется на величину Δx.

Определение 2

Дифференциал от дифференциала называется дифференциалом второго порядка. Таким же рекуррентным образом вводятся понятия дифференциалов более высоких порядков.

Формы записи дифференциала

Для нахождения дифференциала независимой переменной рассматривают функцию y = x, учитывая, что x' = 1, а, следовательно:

Отсюда получается формула:

Для второго порядка вводится обозначение d 2 y.

Свойства дифференциала

Существующая таблица производных помогает выделить некоторые свойства дифференциалов, например, для суммы, произведения, частного получаются следующие правила:

Одним из важных свойств является инвариантность (неизменность) формы записи, независимо от того, является ли функция элементарной или композицией элементарных (сложной). Фактически,

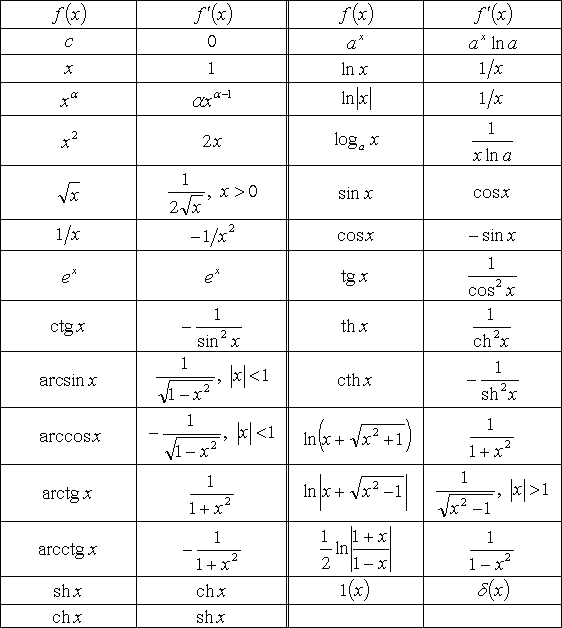
Таблица производных

Примеры решения задач

Задача №1

Найти дифференциал функции

Задача №2

Вычислить значение дифференциала функции

при условии, что

В помощь студентам создан онлайн калькулятор, который позволяет ввести функцию, нажать кнопку и получить форму или значение дифференциала.

Если dx есть константа, то для высших порядков имеет место следующая формула:

Этот результат вытекает непосредственно из определения:

Задача №3

Найти d 2 y, если y = cos2x и x – независимая переменная.

Если x – функция от некоторой другой независимой переменной, то свойство инвариантности перестаёт работать, следовательно,

Задача №4

Найти d 2 y, если y = x 2 и x = t 3 + 1, t – независимый аргумент.

Нетрудно заметить, что если выразить y напрямую через t, то получится тот же результат.

с высокой степенью точности можно вычислить приращение любой дифференцируемой зависимости.

Раскрыв Δy, сделав соответствующие преобразования, приходят к формуле приближённых вычислений:

Задача №5

Вычислить приближённо arctg1,05.

Пусть f(x) = arctg x. Тогда

Полный дифференциал функции

Математика не ограничивается множеством функций одного независимого аргумента. Рассматриваются зависимости от двух и более переменных.

Определения похожи, отличается вид главной части. Рассматриваются несколько слагаемых.

Например, если z = f(x;y) то

Последнее равенство есть формула полного дифференциала. Для функции нескольких переменных сохраняется принцип построения.

Если рассматривают приращения только по одной переменной, то приходят к понятию частных дифференциалов.

Высшая математика позволяет находить приближённо общий корень системы уравнений, пользуясь дифференциальным исчислением, делать прикидку результатов, прогнозировать получаемое.

$\[ \lim_<\Delta x \to 0> \frac = f$

Тогда в некоторой окрестности этой точки отношение

$\[ \frac<\Delta y> = f$

где при Тому приращение функции можно представить в виде:

$\[ \Delta y = f$

При этом величина является бесконечно малой более высокого порядка, чем и бесконечно малая поэтому величину называют главной частью приращения функции .

Дифференциалом функции в точке называют главную, линейную относительно часть ее приращения которая равна произведению производной функции в этой точке на приращение аргумента:

Замечание. Дифференциал называют также дифференциалом первого порядка.

Найдем дифференциал независимой переменной то есть дифференциал функции Так как получаем, что

То есть дифференциал независимой переменной равен ее приращению:

Тогда формула для дифференциала перепишется в виде:

Таким образом, дифференциал функции равен произведению производной указанной функции на дифференциал независимой переменной.

Задание	Найти дифференциал функции
Решение	Согласно определению, искомый дифференциал равен:

Найдем производную заданной функции:

$\[ y$

$dy = \frac<x + 1> dx$

Геометрический и механический смыслы дифференциала функции

Геометрически дифференциал функции в точке равен приращению ординаты касательной к графику функции в рассматриваемой точке, когда переменная получает приращение .

Механический смысл дифференциала. Пусть материальная точка двигается по закону Дифференциал функции равен:

Для фиксированных значений и – это тот путь, который бы прошла материальная точка за время в случае, если она будет двигаться равномерно и прямолинейно с постоянною скоростью

Стоит отметить, что фактический путь в случае неравномерного движения материальной точки, в отличии от дифференциала не является линейной функцией времени а поэтому отличается от пути Но все же, если время является достаточно малым, то скорость движения существенно не изменяется и поэтому движение точки на промежутке времени от до есть практически равномерным.

Основные формулы дифференциала

Основные формулы, которые связаны с дифференциалами, можно получить, используя связь между дифференциалом функции и ее производной, то есть тот факт, что а также соответствующие формулы для производных.

Рассмотрим две дифференцируемые функции и Тогда имеют место следующие равенства:

Дифференциал сложной функции равен произведению производной этой функции по промежуточному аргументу на дифференциал этого промежуточного аргумента, то есть

При решении различных задач геометрии, механики, физики и других отраслей знания возникла необходимость с помощью одного и того же аналитического процесса из данной функции y=f(x) получать новую функцию, которую называют производной функцией (или просто производной ) данной функции f(x) и обозначают символом

Тот процесс, с помощью которого из данной функции f(x) получают новую функцию f ' (x) , называют дифференцированием и состоит он из следующих трех шагов:

1) даем аргументу x приращение ∆ x и определяем соответствующее приращение функции ∆ y = f(x+ ∆ x) -f(x) ;

2) составляем отношение
3) считая x постоянным, а ∆х→ 0 , находим , который обозначаем через f ' (x), как бы подчеркивая тем самым, что полученная функция зависит лишь от того значения x, при котором мы переходим к пределу.

Определение : Производной y ' =f ' (x) данной функции y=f(x) при данном x называется предел отношения приращения функции к приращению аргумента при условии, что приращение аргумента стремится к нулю, если, конечно, этот предел существует, т.е. конечен.

Заметим, что если при некотором значении x, например при x=a, отношение

при ∆х→ 0 не стремится к конечному пределу, то в этом случае говорят, что функция f(x) при x=a (или в точке x=a) не имеет производной или не дифференцируема в точке x=a.

Свойства производных:

1. Если производные функции f и g в точке х ₀ существуют, то существует и производная суммы f + g в этой точке, причем

( f + g )’ (х ₀ )= f ’(х ₀ )+ g ’(х ₀ );

(производная суммы равна сумме производных)

2. Если производные функции f и g в точке х ₀ существуют, то существует и производная произведения fg в этой точке, причем

( fg )’(х ₀ )= f ’(х ₀ ) g (х ₀ )+ f (х ₀ ) g ’(х ₀ );

3. Если производные функции f и g в точке х ₀ существуют и g (х ₀ ) не равные 0, то существует и производная частного f / g в этой точке, причем

В частности, если g ( x )= c , то

( fc )’(х ₀ )=( cf )’(х ₀ )= cf ’(х ₀ )

Понятие и геометрический смысл дифференциала

Определение. Дифференциалом функции в некоторой точке x называется главная, линейная часть приращения функции.

Дифференциал функции y = f(x) равен произведению её производной на приращение независимой переменной x (аргумента).

Это записывается так:

Геометрический смысл дифференциала. Дифференциал функции y = f(x) равен приращению ординаты касательной S, проведённой к графику этой функции в точке M(x; y), при изменении x (аргумента) на величину (см. рисунок).

Почему дифференциал можно использовать в приближенных вычислениях?

Дифференциал, является главной, линейной относительно частью приращения функции; чем меньше , тем большую долю приращения составляет эта часть. В этом можно убедиться, мысленно передвигая перпендикуляр, опущенный из точки P (см. рисунок) к оси Ox, ближе к началу координат. Поэтому при малых значениях (и при ) приращение функции можно приближенно заменить его главной частью , т.е.

О разных формах записи дифференциала

Дифференциал функции в точке x и обозначают

поскольку дифференциал функции y = f(x) равен произведению её производной на приращение независимой переменной.

Замечание. Нужно помнить, что если x – исходное значение аргумента, а - наращенное значение, то производная в выражении дифференциала берётся в исходной точке x ; в формуле (1) этого не видно из записи.

Дифференциал функции можно записать в другой форме:

Пример 1. Найти дифференциалы функций:

Решение. Применяя формулы дифференцироивания степенной и логарифмической функций из таблицы производных, а также формулу (4), находим:

Найти дифференциалы самостоятельно, а затем посмотреть решения

Пример 2. Найти дифференциал функции

1) выделив линейную часть;

Пример 3. Найти дифференциал функции

Пример 4. Найти дифференциал функции

в точках x = 0 и x = 1 .

В основном же задачи на дифференциалы - это более сложные, чем рассмотренные выше для разминки, поэтому стоит посетить страницу с решением задач на дифференциалы сложных функций. Скорее всего, вызывающие у вас трудности задачи именно к таким и относятся.

Свойства дифференциала

В этом и следующем параграфах каждую из функций будем считать дифференцируемой при всех рассматриваемых значениях её аргументов.

Дифференциал обладает свойствами, аналогичными свойствам производной:

(С – постоянная величина) (5)

Формулы (5) – (9) получаются из соответствующих формул для производной умножением обеих частей каждого равенства на .

Применение дифференциала в приближенных вычислениях

Установленное во втором параграфе приближенное равенство

позволяет использовать дифференциал для приближенных вычислений значений функции.

Запишем приближенное равенство более подробно. Так как

Пример 5. Пользуясь понятием дифференциала, вычислить приближенно ln 1,01.

Решение. Число ln 1,01 является одним из значений функции y = ln x . Формула (11) в данном случае примет вид

что является очень хорошим приближением: табличное значение ln 1,01 = 0,0100.

Пример 6. Пользуясь понятием дифференциала, вычислить приближенно

Решение. Число
является одним из значений функции

Так как производная этой функции

то формула (11) примет вид

Вычислить приближенно самостоятельно, а затем посмотреть решение

Пример 7. Вычислить приближенно:

Абсолютная и относительная погрешности приближенных вычислений

Пользуясь приближенным значением числа, нужно иметь возможность судить о степени его точности. С этой целью вычисляют его абсолютную и относительную погрешности.

Абсолютная погрешность приближенного числа равна абсолютной величине разности между точным числом и его приближенным значением:

Относительной погрешностью приближенного числа называется отношение абсолютной погрешности этого числа к абсолютной величине соответствующего точного числа:

Если точное число неизвестно, то

Иногда, прежде чем применить формулу (11), требуется предварительно преобразовать исходную величину. Как правило, это делается в двух целях. Во-первых, надо добиться, чтобы величина была достаточно малой по сравнению с , так как чем меньше , тем точнее результат приближенного вычисления. Во-вторых, желательно, чтобы величина вычислялась просто.

Пример 8. Пользуясь понятием дифференциала, вычислить приближенно . Оценить точность полученного результата.

Решение. Рассмотрим функцию

Её производная равна

а формула (11) примет вид

В данном случае было бы нерационально вычислять приближенно следующим образом:

так как значение

не является малым по сравнению со значением производной в точке

Здесь удобно предварительно вынести из под корня некоторое число, например 4/3. Тогда

Умножая на 4/3, находим

Принимая табличное значение корня

за точное число, оценим по формулам (12) и (13) абсолютную и относительную погрешности приближенного значения:

Читайте также: